点云的球面投影理解

前言

球面投影或正视图投影是将3D点云数据表示为2D图像数据的一种方式，因此从本质上讲，它还充当降维方法。球形投影方法正越来越多地用于处理点云深度学习解决方案中。应用最广泛的领域是对点云中对象进行分类和分割任务，这个投影方法在多个工作中使用，例如：PointSeg，SqueezeSeg， SalsaNet等，以及在上一篇总结到的最新的语义分割网络3D-MiniNet也用到了球面投影。
将点云表示为2D图像的最大优点是，它打通了过去十年中从2D图像到3D点云的研究。例如，各种不同的SoTA深度学习网络，如FCN，U-Net，Mask-RCNN，以及Faster-RCNN，这些优秀的分割/检测网络现在都可以扩展到点云数据中使用，这也是很多研究人员试图完成的目标，尤其是面对自动驾驶领域，每秒接收大量的点云信息，点云数据的计算是庞大耗时的工程。
球面投影的原理实际很简单，我们可能早已经学到过球坐标系，但是可能都没有思考过如何使用，点云的球面投影表示略有不同，现在本文将讨论如何使用球形投影将3D点云投影到图像中。

点云扫描过程

首先我们利用简图了解一下点云的扫描过程，
以16线激光雷达为例：

激光雷达的第一个与最后一个激光器形成的最大视场和最小视场分别表示为FOV_Up和FOV_Down。右边的矩形是将激光雷达形成的空心圆柱投影（投影不是将曲面进行简单地展开，而是一个基坐标系变换的过程）后在2D平面上表示的情况。

根据垂直角分辨率FOV_Up（上部视场）和FOV_Down（下部视场），这16个激光器中的每一个都以固定角度定向。每个激光雷达都有一个发射器和一个接收单元。这些点是通过计算每个激光从物体反射后的飞行时间而形成的。当旋转360度时，这16个激光器形成一个点云。
因此，激光雷达扫描后的点云其几何形状将是一个空心圆柱体，此时激光雷达位于一个坐标系的中心。当我们从垂直于圆柱主轴的轴上看这个空心圆柱时，可将其投影到一个平面上。该图像称为球面投影图像。

变换过程

坐标表示

首先我们再来看一个三维点的简图，只取一个点进行投影演示：

对于上图（左）中的点Point（$x_1，y_2，z_3$），我们需要将其投影到一个2D图像上，来获得新的2D坐标表示。首先左图中假设$X$轴是激光雷达的正视图，即汽车前进的方向，该点与原点的连线将与xy平面（理解为地面）形成一个角度，术语为俯仰角（pitch），该点在$xy$平面的投影与原点的连线与中心线$x$或$xz$平面形成一个偏转角（yaw）。通过使用三角函数，我们可以获得每个点用$x_1，y_2，z_3$表示的俯仰和偏航值。由于原点位于图像的中心，因此这些偏航和俯仰值构成了投影图像的每个像素位置。因此，通过计算每个点的偏航角和俯仰角，我们可以完全形成投影图像。在这一点上，我还要指出，俯仰角的值在[FOV_Up，FOV_Down ]范围内，因为它是激光指向的最大和最小视角，而偏航值的范围是[$-\pi$，$\pi$]。
我们得出在旧坐标系中俯仰角和偏航角的表示方式：

$$\begin{array}{l}\text{ pitch }={\sin }^{-1}(z_1/\mathrm{R})=\arcsin (z_1/\mathrm{R})\\ \text{ yaw }={\tan }^{-1}(y_1/x_1)=\arctan (y_1/x_1)\end{array}\text{\hspace{1em}(1)}$$有些时候使用如下变形：
$$\begin{array}{l}\text{ yaw }={\tan }^{-1}(y_1/x_1)=\arcsin (y_1/\sqrt{(x_1^2+y_1^2)})\end{array}$$然后对所有的点都可以使用这个公式进行转化，现在的情况是我们可以很容易的将一个本来用 $x，y，z$表示出来的点经过一步计算，获得它的（pitch, yaw）值，这样我们就获得了点的2D表示。但是需要注意的是，虽然现在有了投影图像，由于两个问题，我们仍然无法使用它。首先，我们需要将原点平移到图像的左上角，这是因为在计算机视觉中，规范的原点应位于图像的左上角。其次，我们需要根据所使用的激光雷达的类型来缩放图像。这两个步骤如下所示， 注： 这里使用（ $yaw，pitch$）坐标表示是个人横纵坐标理解上的习惯，实际应使用（ $pitch,yaw$）坐标形式，最后变换的（ $u,v$）对应坐标( $pitch,yaw$)：

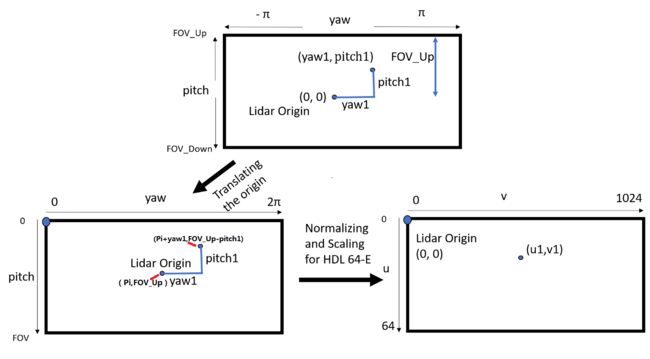
1. 坐标原点变换
首先我们要将激光雷达作为新坐标的原点转移到左上角，如果将激光雷达移动到左上角，其他投影点都需要根据点和激光雷达的相对位置关系（上图中间一幅简图）进行变换，新的等式坐标变为，变为（ $pitch,yaw$）坐标格式：
$$\begin{array}{l}\text{ pitch }={\mathrm{F}\mathrm{O}\mathrm{V}}_{-}\mathrm{U}\mathrm{p}\text{ - pitch1 }\\ \text{ yaw}=\mathrm{y}\mathrm{a}\mathrm{w}1+\pi \end{array}\text{\hspace{1em}(2)}$$

2.规范化和缩放
该步骤是必需的，因为对于不同类型的激光雷达，投影图像的大小将有所不同，主要目的是在投影图像中尽可能多地适应点。
正如在上面观察到的那样，球面投影的整个过程实际是种降维，因此，这是我们会丢失原始点云数据中的空间信息。这里的想法是所形成投影图像的尺寸能够帮助我们从图像中的点云中捕获最相关的点。
因此可以看出，激光雷达的激光数量应等于投影图像的宽度。图像的每一行会是从激光雷达的每个激光器获得的点。此记为row_scale，并乘以归一化的俯仰轴。举个例子，Velodyne HDL 64-E激光雷达具有64个激光器，因此，上面变换得到的坐标值值乘以俯仰轴，将投影图像的宽度设置为64。
而图像的长度构成了偏航角上的分辨率。可以调整此参数以使其得到尽可能多的点。投影图像的长度称为col_scale，并与标准化偏航轴相乘以获得最终图像尺寸。同样，对于HDL 64-E，最大水平分辨率为0.35度。因此，在最坏的情况下，每个激光至少可以得到（360 / 0.35 = 1028）点。在深度学习和卷积网络中，图像大小习惯设置为2的倍数。因此，长度为1024的图像将适合图像中的最大点数，并将此值乘以偏航轴。
最终得出，64X1024的图像尺寸非常适合HDL 64-E。对于Velodyne VLP-16可以进行类似的计算，其中最佳图像尺寸为16x1024。现在可以将规范化方程式重写为：

$$\begin{array}{l}\text{ normalized\_pitch }=\left({\mathrm{F}\mathrm{O}\mathrm{V}}_{-}\mathrm{U}\mathrm{p}-\text{ pitch }\right)/\left({\mathrm{F}\mathrm{O}\mathrm{V}}_{-}\mathrm{U}\mathrm{p}-{\mathrm{F}\mathrm{O}\mathrm{V}}_{-}\text{Down }\right)\\ \text{ normalized\_yaw }=(yaw+\pi )/2\pi \end{array}\text{\hspace{1em}(3)}$$注意这里认为 $FO{V}_{\_}Down$为负数，所以 $FOV=FO{V}_{\_}Up+abs(FO{V}_{\_}Down)=2\times FO{V}_{\_}Up$
因此，将第 (1)个等式带入 (3)，可以得到原3D点云在最终（ $u,v$）坐标系下的最终表示为：
$$\left(\begin{array}{c}u\\ v\end{array}\right)=\left(\begin{array}{c}\left[1-\left(\arcsin \left(z/R\right)+{\mathrm{F}\mathrm{O}\mathrm{V}}_{\mathrm{u}\mathrm{p}}\right){\mathrm{F}\mathrm{O}\mathrm{V}}^{-1}\right]\times row\_scale\\ \frac{1}{2}\left[1+\arctan (y/x){\pi }^{-1}\right]\times col\_scale\end{array}\right)\text{\hspace{1em}(4)}$$对于Velodyne HDL 64-E激光雷达，只需要将 $col\_scale，row\_scale$，分别赋值64和1024就可以了。
注意最后这个等式和上一篇中提到的3D-MiniNet使用的公式表示形式略有不同，但实际上一样，上一篇论文中使用 $W\times H$分别对应于投影图像的宽和高，我们的推导过程是使用了 $col\_scale\times row\_scale$,我们将图片的用长度和宽度表示，本质上是一致的，使用的时候注意统一格式就行。
因此，借助上述方程式，我们可以将云的每个点（ $x，y，z$）投影到其相应的球形投影（ $u，v$）中。
在对点云的实际使用中，在获得投影表示后不是单单使用这个投影的2维特征信息，实际上我们会加入原始坐标（ $x,y,z$）以 $R$表示欧式点与激光器原点的欧氏距离或则范围值， $I$表示点云的强度大小，事实上（ $x,y,z,I$）都是激光雷达直接测得的数据，唯一需要计算的是 $R$,这样我们的投影图像的真实维度为： $激光雷达线程数\ast 投影图像的宽度\ast 5(加入的5个通道)。$
可以使用PCL和OpenCV可视化球面投影的图像。
C++代码主体实现部分：

#include 
#include  // For visualizing image
#include   // For PCL Point Cloud
#include     // For Reading the Cloud
#include   // For PCL different cloud types

#include 

SphericalConversion::SphericalConversion(const Configuration& config)
    : config_(config) {
  spherical_img_.assign(config_.num_lasers,
                        std::vector<std::vector<double>>(
                            config_.img_length, std::vector<double>(5, 0.0)));
  cloud_ =
      pcl::PointCloud<pcl::PointXYZI>::Ptr(new pcl::PointCloud<pcl::PointXYZI>);
};

int SphericalConversion::LoadCloud(const std::string& path) {
  // Loading from Bin File
  if (pcl::io::loadPCDFile<pcl::PointXYZI>(path, *cloud_) == -1) {
    std::cout << "Couldn't read the cloud file at: " << path << "\n";
    return -1;
  }
  return 1;
}
int SphericalConversion::MakeImage() {
  // Converting to Radians
  double fov_up_rad = (config_.fov_up / 180) * M_PI;
  double fov_down_rad = (config_.fov_down / 180) * M_PI;
  // Getting total Field of View
  double fov_rad = std::abs(fov_up_rad) + std::abs(fov_down_rad);
  if (cloud_->size() == 0) {
    std::cerr << "Empty Point Cloud_" << std::endl;
    return -1;
  }
  for (auto point : *cloud_) {
    // Getting Pixel from Point
    int pixel_v = 0;
    int pixel_u = 0;
    double range = 0.0;
    GetProjection(point, fov_rad, fov_down_rad, &pixel_v, &pixel_u, &range);
    spherical_img_.at(pixel_u).at(pixel_v) =
        std::vector<double>{point.x, point.y, point.z, range, point.intensity};
  }
  return 1;
}

void SphericalConversion::GetProjection(const pcl::PointXYZI& point,
                                        const double& fov_rad,
                                        const double& fov_down_rad,
                                        int* pixel_v, int* pixel_u,
                                        double* range) const {
  // range of Point from Lidar
  *range = sqrt(point.x * point.x + point.y * point.y + point.z * point.z);
  //  Getting the angle of all the Points
  auto yaw = atan2(point.y, point.x);
  auto pitch = asin(point.z / *range);
  // Get projections in image coords and normalizing
  double v = 0.5 * (yaw / M_PI + 1.0);
  double u = 1.0 - (pitch + std::abs(fov_down_rad)) / fov_rad;
  // Scaling as per the lidar config given
  v *= config_.img_length;
  u *= config_.num_lasers;
  // round and clamp for use as index
  v = floor(v);
  v = std::min(config_.img_length - 1, v);
  v = std::max(0.0, v);
  *pixel_v = int(v);

  u = floor(u);
  u = std::min(config_.num_lasers - 1, u);
  u = std::max(0.0, u);
  *pixel_u = int(u);
}

auto SphericalConversion::GetImg() const { return spherical_img_; }

void SphericalConversion::ShowImg(
    const std::vector<std::vector<std::vector<double>>>& img) const {
  cv::Mat sp_img(img.size(), img.at(0).size(), CV_64FC1);
  for (int i = 0; i < sp_img.rows; ++i) {
    for (int j = 0; j < sp_img.cols; ++j) {
      sp_img.at<double>(i, j) = img.at(i).at(j).at(4); //Intensity value
    }
  }
  cv::imshow("Intensity Image", sp_img);
  cv::waitKey(0);
}

int main() {
  /** For Velodyne HDL 64-E
   * Fov_Up = 2 degrees
   * Fov_Down = -24.8 degrees
   * Num of Lasers = 64
   * Best length of image comes out to be = 1024
   */
  const Configuration config_input{2, -24.8, 64, 1024};
  const std::string path =
      "/home/" + std::string(getenv("USER")) +
      "/OpenSource_Problems/Spherical_View_Projection/assests/"
      "test_cloud.pcd";
  std::cout << path << std::endl;
  SphericalConversion conv(config_input);
  conv.LoadCloud(path);
  conv.MakeImage();
  auto img = conv.GetImg();
  conv.ShowImg(img);
}

结果展示：

1. 图像分为上下两部分，上方为球形投影球形效果，下方为点云可视化效果，上方图像的每一行对应于从激光雷达的每个激光获得的点。在此，图像中的最低行对应于激光雷达中的最低激光，是激光雷达附近最接近的环，如上所示。
2. 形成的球形图像本质上是环形的，这意味着将能够观察到：当物体从左侧离开图像时，它们可能会重新出现在图像的右侧。
3. 可以用人眼识别图像中的对象。这意味着，如果您查看图像，则很容易区分汽车，自行车，建筑物，道路等。而且如果人眼可以分辨，那么在这种图像上训练的深度网络很有可能给出良好的分割和分类结果。
4. 在此投影中丢失的点是那些与激光雷达中心的俯仰和偏航角相同但范围值不同的点。因此，将激光雷达中心连接到该点的射线上的点中只有一个会被捕获在投影图像中。
   文章来源
   实验使用的数据和的头文件

总结

点云的球面投影是和很好的点云降维处理工具，以图片的方式表示点云的数据，一旦这样表示我们就可以利用很多成熟的二维图片的处理方法进行扩展，且计算量较少，适合实时系统的要求，这种投影方式方式在机器人和自主驾驶等任务中得到应用。