深度学习之路（3）神经网络结构和参数优化

书籍参考

参考英文在线书籍 Neural Networks and Deep Learning 第三章。
对应原文Chapter3内容特别好。作者为了让读者直观感受学习过程，还嵌入了算法和图，读者可以点击相应按钮看到神经网络的学习过程——其Cost随Epoch的变化曲线。

博文提要

前面讲了神经网络学习过程的重要环节——梯度下降法，重点讲了该方法用的反向传播原理，它大大减小了梯度求算的时间复杂度。
我们在了解机器学习算法之初，可能就听说过算法工程师的日常工作——调参。不同于上面学习过程的调参（算法自动调节神经元内部参数w、b），这里的调参是调整超参数，由我们决定怎么设置。知道一个神经网络的结构和参数的含义，才能更好地理解调参方向，才不像无头苍蝇一样靠运气调参。本篇着重介绍神经网络的优化和超参数的调整，包括技巧和原理。如果你对这些问题感兴趣，请继续读下去：

1. 代价函数怎么优化？
2. 交叉熵代价函数怎么来的？
3. 什么是过拟合？怎么解决？
4. 正则化有哪些方式？
5. 神经网络初始参数w、b怎么选择？
6. 神经网络各种超参数怎么确定？

一、学习饱和与cost function优化

1. 交叉熵函数

上篇讨论了反向传播算法求梯度的过程，代价函数C的梯度由两个偏微分组成：


其中δ为：

我们发现一个问题！δ含有因数σ’，我们知道σ(z)函数曲线是s形的，当z很小或者很大时，都有σ’->0，此时δ就会很小；δ很小导致C梯度很小，导致调参很慢（饱和）！
原文嵌入了程序和动态图表展示，让我们直观看到cost随训练次数epoch下降的过程，有兴趣的可以自己看下http://neuralnetworksanddeeplearning.com/chap3.html。
下面考虑如何解决这个问题。一个思路是改造方差形式的代价函数：

其中a=σ(z)，可得C’_z=(a-y)σ’(z)。我们想消掉σ’，可以用交叉熵函数代替。这个交叉熵函数来的有点突然，我们的思路是：假设C对z的导数不含σ’，只含有(a-y)或者说σ(z)-y，我们可以通过对z积分得到一个函数，它就是交叉熵函数：

(a-y)对w、b的积分过程有点复杂，有兴趣的可以自己推导。我们可以用上式对z求微分进行验证，发现确实消除了σ’项：


分析上式，发现它有个优点，误差σ(z)-y越大，微分越大，梯度就越大，那么调参幅度就越大（此处大描述的都是绝对值）。换句话说，误差越大，学习过程就越快！这是我们要的结果。
为了对交叉熵函数有个更直观的认识，有必要提一下：交叉熵是信息论的概念，是对“惊讶”的度量。如果神经元想计算 x→y=y(x)，但实际计算 x→a=a(x)，如果我们认为a是神经元认为y=1的概率，1-a是y=0的概率，交叉熵就是我们的“惊讶”程度。输出是我们期望的值，我们“惊讶”程度就较低；输出越偏离我们的期望值，我们“惊讶”程度越高。想了解更多交叉熵的知识，可以参考这篇完美解释交叉熵。
另外，交叉熵函数恒为正值，且神经网络的输出a跟正确输出y差值越大时，交叉熵也越大。因此，交叉熵可以作为cost function来使用。

2. Softmax

大部分时候，用交叉熵函数都能解决问题。还有一种softmax函数，可以作为激活函数，结合另一种cost function，也能解决学习慢（饱和）问题。这里简单介绍一下。
基本思想是，在输出层使用softmax代替sigmoid激活函数，softmax形式是：

通过下图可以看出，自然指数的作用是将各神经元z的相对差距放大，大者更大，小者更小。

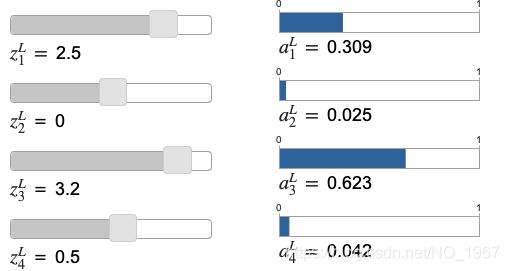
从公式可以看出，第L层（输出层）神经元的激活值范围都是(0,1)。且所有神经元的激活值相加等于1，所以我们可以将softmax看作概率分布。用数字识别的例子解释：a_j^L是第j个神经元的输出，表示识别结果为j的概率。

为适应输出层激活函数的变化，我们用对数形式作cost function：

当识别数字时，如果y是7，那么C=-ln a₇^L，如果我们的神经网络识别精度高，则它会认为概率a₇^L很大，接近1。所以代价-ln a₇^L就很小了。故上面对数形式的函数，符合我们对代价函数的基本要求——可以衡量cost。
那存在学习饱和问题吗？我们看下C对w和b的偏导：

这个结果跟交叉熵的一样，故也不存在σ’导致的学习饱和问题。
也就是说，这两种方式都能解决饱和问题：
a. 输出函数用sigmoid，代价函数用交叉熵函数
b. 输出函数用softmax，代价函数用自然对数形式。

二、过拟合与正则化

在一个模型中，参数的个数有必要引起我们的注意。数学家冯诺伊曼说过：四个参数可以容纳一头大象，五个参数可以让大象鼻子扭起来。
他的意思是，数个参数就可以给我们极大的自由度来描述事物。反观我们的神经网络（748,30,10），有23860个参数，深度网络则有上亿甚至更多参数！参数这么多，潜在的问题就是过拟合。

1、过拟合

作者做了个实验，用的是交叉熵函数，探究参数对神经网络行为的影响：

参数	隐含层神经元数	学习因子	训练集数目	batch大小	epoch
取值	30	0.5	1000	10	400

跟之前的区别在于，训练集变小，相应的epoch增大，学习因子也做了调整。结果cost趋势还不错：

但是训练后，对测试集识别的精确度很低，在82.2%波动：

再看测试集的cost趋势：

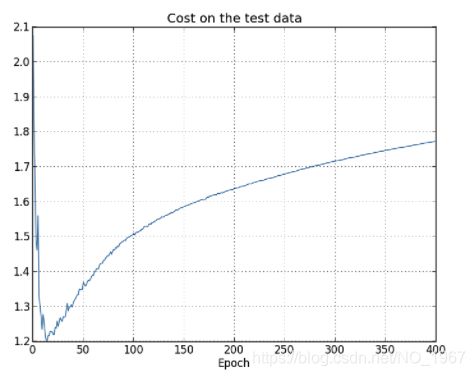
随着训练次数增加，测试集对应的cost反而上升了！这就是过拟合的信号。我们可以检测测试集cost，检测到它在一定epoch后不再减小，则停止训练，即提前结束来避免过拟合。过拟合的另外一个信号是，训练集对应的精确度达到100%：

参数过多是过拟合的原因之一，训练数据情况不好是另一个（训练数据不能覆盖普遍情况）。对过拟合的通俗理解是，神经网络对训练集的细节了解过多，导致无法正确识别没见过的测试集数据。
如果增大训练集到50000，再看其识别精度：

过拟合虽然仍存在，但情况好了很多（从之前的17.8%到现在的2.5%），这就是增大训练数据集对减轻过拟合的作用。有时候获取更多数据不是一件容易的事，没关系，另一个减轻过拟合的方法是正则化。

2. 权重衰减（L2）正则化

权重衰减正则化后的交叉熵代价函数：

也称作L2正则化，表示增加了w²的项——正则项。
类似地，也可以对均方差形式的代价函数正则化：

忽略代价函数原来的形式，都用C₀表示，则二者都能简写为：

直观地看，代价函数引入了权重，要让C小，各w就得小。换句话说，神经网络倾向于学习大小更均匀的权重，避免某个权重过大，此处说过大是相对而言的：相对于权重增大对C₀减小的贡献，它对正则项增大的贡献更大。所以，正则化是一种折中手段，一要cost小，二要避免权重过大。正则项中的λ则可以控制二者比重，λ越大，越会避免权重过大。
采用正则化处理后，超参数增加了λ，再测试神经网络学习的结果。

参数	隐含层神经元数	学习因子	训练集数目	batch大小	epoch	λ
取值	30	0.5	1000	10	400	0.1

对测试数据识别的精度有了不少提升：

如果现在增大训练数据集为50000，epoch=30，相应地修改λ=5，其他不变。然后得到识别精度：

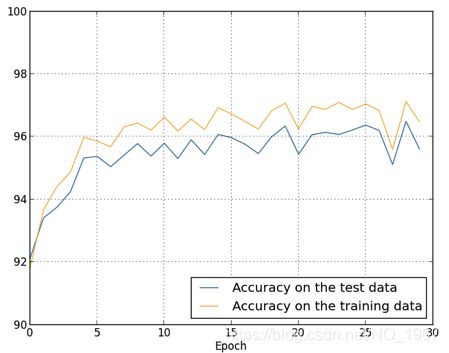
提升了更多。最后的实验是，隐含层用100个神经元，epoch=60，η=0.1，λ=5，其他参数同上。得到了98%以上的精确度。
在不使用正则化时，会遇到学习“止步不前”的情况。原文给了一个启发性的理解：权重向量在各维度上可能很不均等，按梯度下降法，每次调整一点，所引起的权重向量方向上的变化极小，导致学习进度太慢。有了正则化后，权重之间的悬殊减小，同样大小的调整，权重向量的方向可以更灵活的变化。这是正则化带来的另一个好处。

3. 其他方法

a. L1正则化

解决过拟合问题的方法，除了L2正则化，还有L1正则化，原理跟L2类似。

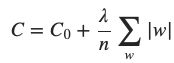
b. Dropout（剔除法）

Dropout是另外一种思路：每次用一个batch数据训练时，只随机选用隐含神经元的一半，另一半参数都设为零（相当于剔除了，对网络没有贡献），调整w、b之后存下来。对下一batch，重复随机选一半神经元的过程，通过梯度下降法得到新一批w、b。一直重复这个过程，就可以得到一系列w、b。
结束之后，每个w、b除以2，作为最终学习得到的参数。这是因为半数神经元就可以达到想要的输出值，现在想用所有的神经元，输出会是用半数神经元的2倍。
Dropout过程很特别，但是不难理解。每批数据训练半数神经元，不同批次训练的神经元“方向”不同，最后得到的是“平均方向”，对细节的关注变少，就解决了过拟合问题。

扩展训练数据集

人工增加训练数据，比如对于数字识别，可以对训练集的原图片做小角度的旋转生成新的数据；或者增加些噪声等等。

4.为什么正则化可以削弱过拟合

有一个很好理解的例子，就是线性拟合。它比我们的神经网络简单，可以做下类比以方便理解。

对于上面散点，怎么画一条线来拟合其分布。可以用九阶多项式曲线y=a₀x⁹+a₁x⁸+…+a₉：

也可以用一条直线y=2x来拟合：

俩曲线哪个更符合真实情况呢？第一个穿过了所有点，但形式复杂；第二个没穿过所有但简单。模型是为了预测，未来的散点会怎样分布？如果更符合线性，那九阶多项式相对来说就是过拟合了，我们的线性模型之所以不能穿过所有点是因为有噪声。而九阶模型学习到了噪声，所以对训练数据很合适，但不适用于没见过的数据。
对于神经网络来说，若所有神经元都有小的权重，这表明输出不会跟随输入的小变化而大幅变化（对比着看，九次项会大幅变化）。这样就避免受噪声影响而发生过拟合。简言之，正则化让网络倾向基于常见特征构建简单模型。
一般我们会使用简单的模型（奥卡姆剃刀原则）。但是对于现实世界，选择复杂或是简单模型，没有标准答案，复杂的可能更准确（例如相对论颠覆了牛顿力学）。

三、权重的初始化

在初始化神经网络时，可以用标准正态分布（高斯分布）生成w参数，即均值为0，标准差为1。这小节探讨更好的初始化参数。
假设有个神经网络有1000个输入神经元，我们使用标准化正态分布来初始化w、b。我们只关注第一隐含层的第一个神经元。

如果1000个神经元中有500输出1、500输出0，那么加权和是z=∑_jw_jx_j+b 只含有501个项。w、b都是独立的标准正态分布，故z也是正态分布，其均值为0，标准差为√501≈22.4。就是说z有很宽的正态分布：

上图表示z取值的概率分布，它有较均匀的可能性取一个大范围内的任意值（钟形较宽）。如果用sigmoid作激活函数的话，这是存在问题的，我们前面已经探讨的学习饱和问题，sigmoid会在|z|取值很大时饱和。为了避免此问题，我们可以简单修改一下z标准差为更小的值。这个更小的值可以由权重参数个数n决定，让各权重使用这样的正态分布：均值为0，标准差为1/√n。这样的话，对于上面情况（输入500个0，500个1），z的正态分布标准差就变成了√(3/2)=1.22。z更不易取到太大的值而导致饱和，因为z的正态分布变得更加窄和高了：

这是权重初始化方式对学习精度的影响：

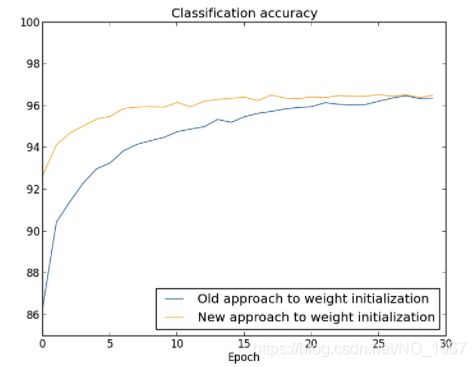
最终识别精度差不多，但是新方法让学习更快速。

四、神经网络超参数的选择

终于说到了超参数的选择。超参数包括学习率η，正则化参数λ ，等等。前面数字识别所用参数是经过测试确定的，我们怎么测试确定呢？
考虑一个随机情况，比如隐含层用30个，cost function选交叉熵函数，λ=1000，η=10. 运行过程如下：

准确度在10%左右，跟随机猜没多少区别。我们没法事先知道哪个参数有问题，也不知道调参方向。

1. 通用的策略

可以通过缩小问题规模，用控制变量法先确定一个超参的数量级，再缩小范围调节它。
缩小问题规模：剔除隐含层神经元，只用1000个测试数据，每批10个，100个作测试集，λ=1000（图中lmbda）。缩小规模可以快速计算，快速得到反馈，我们看下精度：

仍然跟随机猜精度一样。但是一秒就可以得到结果，这就是缩小规模的好处。
现在，修改λ=20（为了确定数量级，可以往大/小方向大幅修改）再看结果：

有了提升，看来方向对了。如果暂定lmbda为20，修改学习率η=100（上面为10）测试一下：

又糟了，所以再反向试下η=1：

好多了，方向没错。现在可以继续优化η，或回头单独调整λ到一个不错的值。然后，让问题复杂点，比如增加一个隐含层有10神经元，再调整η、λ。然后隐含层增加到20个神经元，重复调整……这个办法看起来很不错，但不排除让你陷入困境，花几天也找不到方向。所以有必要强调，必要时要再缩小问题规模，让你得到更快的反馈。

2. 学习率η

η决定了学习的快慢，是重要的超参数，我们重点关注下它。假设为了确定η数量级，先选用三个值，2.5，0.25，0.025，然后得到cost的变化：

可以看到η=2.5时没法好好学习，波动很大。通过梯度下降过程来看，梯度下降调参幅度太大，导致经过“谷底”到了另一边（小球冲过谷底冲到另一边）η=0.025时，学习太慢（小球一步滚动一点点）。

我们可以这样选定η：找到一个η值让cost在前几个epoch时下降然后进入波动（不必太精确），然后选用η=η/2。这样的η让学习既不会太慢，也不会一开始就震荡。
另外，可以每个epoch测试下精度，在精度不再提升时就停止训练，这样可以避免过拟合，加速调参过程。
关于η还有一点需要提醒，我们都将它作为定值用于完整一组epoch的训练，但是它也可以渐变，在开始较大，然后逐渐减小。

3. Mini-batch大小

采用随机梯度下降法，每批数据用多少呢？假设batch-size=1（即在线学习）. 可以想到，每次调整的误差很大（跟每批十个相比）。实际上误差不是大问题，我们要的是学习过程中的cost保持下降。就好像你正试图到达北极，但有一个摇摇晃晃的指南针，每次你看它都会偏离10-20度。如果你经常停下来检查指南针，而且指南针的平均方向正确，你最终会很好地到达北极。
但是batch-size=1不能充分利用硬件的并行计算能力。其实选择batch-size是对计算能力和快速更新w、b的折中。从实用角度考虑，可以画出不同batch-size下精确度随时间的变化曲线，哪个提升最快，就用哪个batch-size。

4. 总结

超参数调节自由度和范围大，所以调参并不容易。但有些好的方法可以参考：

• Practical recommendations for gradient-based training of deep architectures
• Efficient BackProp
• Neural Networks: Tricks of the Trade