NNDL 实验七 循环神经网络（1）RNN记忆能力实验

循环神经网络（Recurrent Neural Network，RNN）是一类具有短期记忆能力的神经网络．

在循环神经网络中，神经元不但可以接受其他神经元的信息，也可以接受自身的信息，形成具有环路的网络结构．

和前馈神经网络相比，循环神经网络更加符合生物神经网络的结构．

目前，循环神经网络已经被广泛应用在语音识别、语言模型以及自然语言生成等任务上．

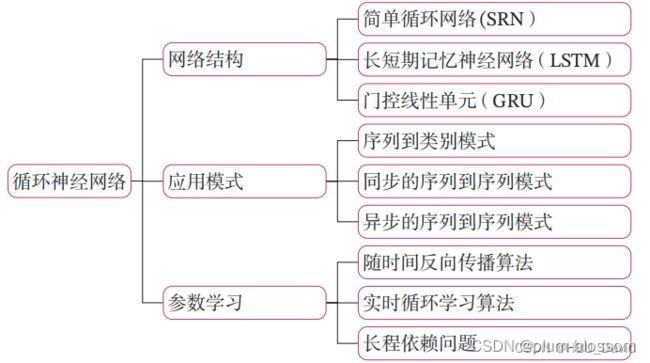
简单循环网络在参数学习时存在长程依赖问题，很难建模长时间间隔（Long Range）的状态之间的依赖关系。

为了测试简单循环网络的记忆能力，本节构建一个【数字求和任务】进行实验。

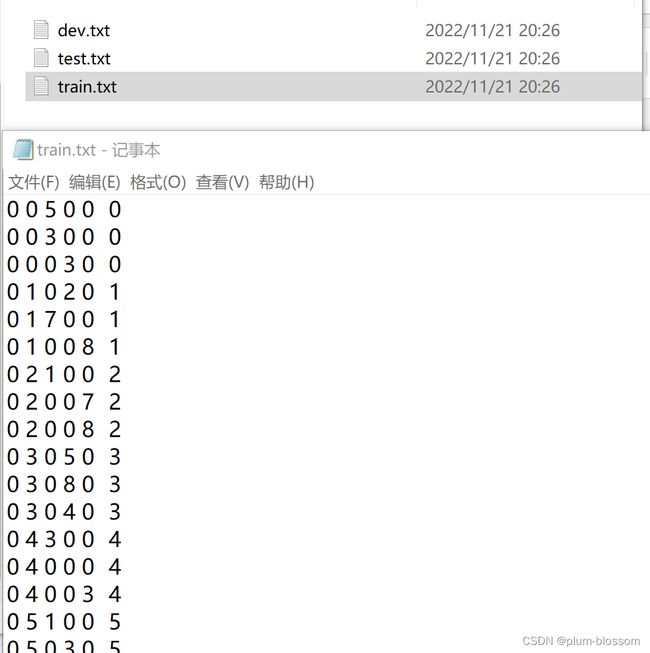
数字求和任务的输入是一串数字，前两个位置的数字为0-9，其余数字随机生成（主要为0），预测目标是输入序列中前两个数字的加和。图6.3展示了长度为10的数字序列．

6.1 循环神经网络的记忆能力实验

循环神经网络的一种简单实现是简单循环网络（Simple Recurrent Network，SRN）

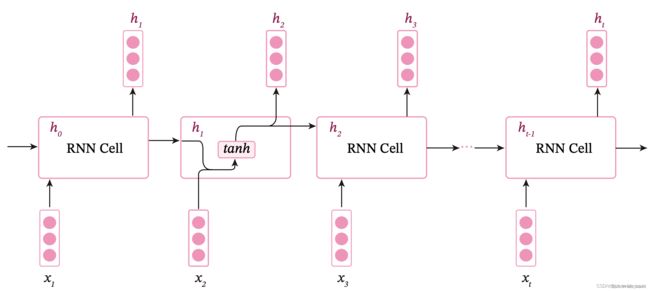
简单循环网络在参数学习时存在长程依赖问题，很难建模长时间间隔（Long Range）的状态之间的依赖关系。为了测试简单循环网络的记忆能力，本节构建一个数字求和任务进行实验。

数字求和任务的输入是一串数字，前两个位置的数字为0-9，其余数字随机生成（主要为0），预测目标是输入序列中前两个数字的加和。图6.3展示了长度为10的数字序列．

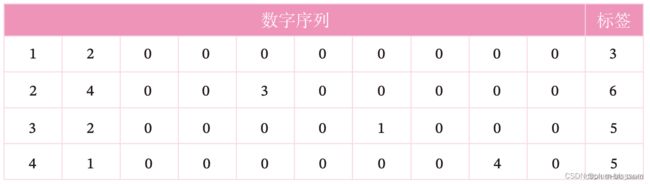
如果序列长度越长，准确率越高，则说明网络的记忆能力越好．因此，我们可以构建不同长度的数据集，通过验证简单循环网络在不同长度的数据集上的表现，从而测试简单循环网络的长程依赖能力.

6.1.1 数据集构建

构建不同长度的数字预测数据集DigitSum

6.1.1.1 数据集的构建函数

import random
import numpy as np

# 固定随机种子
random.seed(0)
np.random.seed(0)

def generate_data(length, k, save_path):
    if length < 3:
        raise ValueError("The length of data should be greater than 2.")
    if k == 0:
        raise ValueError("k should be greater than 0.")
    # 生成100条长度为length的数字序列，除前两个字符外，序列其余数字暂用0填充
    base_examples = []
    for n1 in range(0, 10):
        for n2 in range(0, 10):
            seq = [n1, n2] + [0] * (length - 2)
            label = n1 + n2
            base_examples.append((seq, label))
    
    examples = []
    # 数据增强：对base_examples中的每条数据，默认生成k条数据，放入examples
    for base_example in base_examples:
        for _ in range(k):
            # 随机生成替换的元素位置和元素
            idx = np.random.randint(2, length)
            val = np.random.randint(0, 10)
            # 对序列中的对应零元素进行替换
            seq = base_example[0].copy()
            label = base_example[1]
            seq[idx] = val
            examples.append((seq, label))

    # 保存增强后的数据
    with open(save_path, "w", encoding="utf-8") as f:
        for example in examples:
            # 将数据转为字符串类型，方便保存
            seq = [str(e) for e in example[0]]
            label = str(example[1])
            line = " ".join(seq) + "\t" + label + "\n"
            f.write(line)

    print(f"generate data to: {save_path}.")

# 定义生成的数字序列长度
lengths = [5, 10, 15, 20, 25, 30, 35]
for length in lengths:
    # 生成长度为length的训练数据
    save_path = f"./datasets/{length}/train.txt"
    k = 3
    generate_data(length, k, save_path)
    # 生成长度为length的验证数据
    save_path = f"./datasets/{length}/dev.txt"
    k = 1
    generate_data(length, k, save_path)
    # 生成长度为length的测试数据
    save_path = f"./datasets/{length}/test.txt"
    k = 1
    generate_data(length, k, save_path)

运行结果：

6.1.1.2 加载数据并进行数据划分

import os
# 加载数据
def load_data(data_path):
    # 加载训练集
    train_examples = []
    train_path = os.path.join(data_path, "train.txt")
    with open(train_path, "r", encoding="utf-8") as f:
        for line in f.readlines():
            # 解析一行数据，将其处理为数字序列seq和标签label
            items = line.strip().split("\t")
            seq = [int(i) for i in items[0].split(" ")]
            label = int(items[1])
            train_examples.append((seq, label))

    # 加载验证集
    dev_examples = []
    dev_path = os.path.join(data_path, "dev.txt")
    with open(dev_path, "r", encoding="utf-8") as f:
        for line in f.readlines():
            # 解析一行数据，将其处理为数字序列seq和标签label
            items = line.strip().split("\t")
            seq = [int(i) for i in items[0].split(" ")]
            label = int(items[1])
            dev_examples.append((seq, label))

    # 加载测试集
    test_examples = []
    test_path = os.path.join(data_path, "test.txt")
    with open(test_path, "r", encoding="utf-8") as f:
        for line in f.readlines():
            # 解析一行数据，将其处理为数字序列seq和标签label
            items = line.strip().split("\t")
            seq = [int(i) for i in items[0].split(" ")]
            label = int(items[1])
            test_examples.append((seq, label))

    return train_examples, dev_examples, test_examples

# 设定加载的数据集的长度
length = 5
# 该长度的数据集的存放目录
data_path = f"./datasets/{length}"
# 加载该数据集
train_examples, dev_examples, test_examples = load_data(data_path)
print("dev example:", dev_examples[:2])
print("训练集数量：", len(train_examples))
print("验证集数量：", len(dev_examples))
print("测试集数量：", len(test_examples))

运行结果：

6.1.1.3 构造Dataset类

为了方便使用梯度下降法进行优化，我们构造了DigitSum数据集的Dataset类，函数__getitem__负责根据索引读取数据，并将数据转换为张量。代码实现如下：

from PIL import Image
from torch.utils.data import Dataset
class DigitSumDataset(Dataset):
    def __init__(self, data):
        self.data = data
    
    def __getitem__(self, idx):
        example = self.data[idx]
        seq = torch.tensor(example[0], dtype="int64")
        label = torch.tensor(example[1], dtype="int64")
        return seq, label
    
    def __len__(self):
        return len(self.data)
        

6.1.2 模型构建

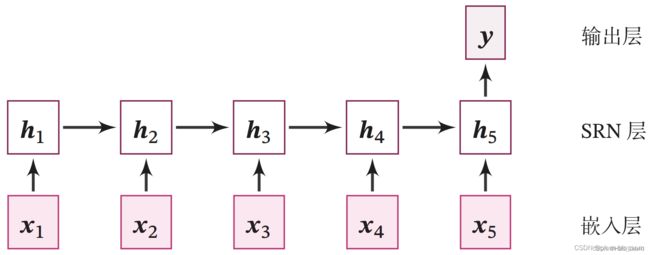
整个模型由以下几个部分组成：
（1） 嵌入层：将输入的数字序列进行向量化，即将每个数字映射为向量；
（2） SRN 层：接收向量序列，更新循环单元，将最后时刻的隐状态作为整个序列的表示；
（3） 输出层：一个线性层，输出分类的结果.

6.1.2.1 嵌入层

本任务输入的样本是数字序列，为了更好地表示数字，需要将数字映射为一个嵌入（Embedding）向量。嵌入向量中的每个维度均能用来刻画该数字本身的某种特性。由于向量能够表达该数字更多的信息，利用向量进行数字求和任务，可以使得模型具有更强的拟合能力。

import torch.nn as nn
 
 
class Embedding(nn.Module):
    def __init__(self, num_embeddings, embedding_dim):
        super(Embedding, self).__init__()
        W_attr = torch.randn([num_embeddings, embedding_dim])
        W_attr = torch.nn.init.xavier_uniform_(torch.as_tensor(W_attr, dtype=torch.float32), gain=1.0)
        # 定义嵌入矩阵
        self.W = torch.nn.Parameter(W_attr)
 
    def forward(self, inputs):
        # 根据索引获取对应词向量
        embs = self.W[inputs]
        return embs
 
 
emb_layer = Embedding(10, 5)
inputs = torch.tensor([0, 1, 2, 3])
emb_layer(inputs)

6.1.2.2 SRN层

自定义简单循环网络
飞桨框架内置了SRN的API torch.nn.SimpleRNN
将自己实现的SRN和Torch框架内置的SRN返回的结果进行打印展示

将自己实现的SRN与Paddle内置的SRN在输出值的精度上进行对比

在进行实验时，首先定义输入数据inputs，然后将该数据分别传入Paddle内置的SRN与自己实现的SRN模型中，最后通过对比两者的隐状态输出向量。

import torch
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(0)
 
 
# SRN模型
class SRN(nn.Module):
    def __init__(self, input_size,  hidden_size, W_attr=None, U_attr=None, b_attr=None):
        super(SRN, self).__init__()
        # 嵌入向量的维度
        self.input_size = input_size
        # 隐状态的维度
        self.hidden_size = hidden_size
        W_attr = torch.randn([input_size, hidden_size])
        W_attr = torch.nn.init.xavier_uniform_(torch.as_tensor(W_attr, dtype=torch.float32), gain=1.0)
        U_attr = torch.randn([hidden_size, hidden_size])
        U_attr = torch.nn.init.xavier_uniform_(torch.as_tensor(U_attr, dtype=torch.float32), gain=1.0)
        b_attr = torch.randn([1, hidden_size])
        b_attr = torch.nn.init.xavier_uniform_(torch.as_tensor(b_attr, dtype=torch.float32), gain=1.0)
        # 定义模型参数W，其shape为 input_size x hidden_size
        self.W = torch.nn.Parameter(W_attr)
        # 定义模型参数U，其shape为hidden_size x hidden_size
        self.U = torch.nn.Parameter(U_attr)
        # 定义模型参数b，其shape为 1 x hidden_size
        self.b = torch.nn.Parameter(b_attr)
 
    # 初始化向量
    def init_state(self, batch_size):
        hidden_state = torch.zeros([batch_size, self.hidden_size], dtype=torch.float32)
        return hidden_state
 
    # 定义前向计算
    def forward(self, inputs, hidden_state=None):
        # inputs: 输入数据, 其shape为batch_size x seq_len x input_size
        batch_size, seq_len, input_size = inputs.shape
 
        # 初始化起始状态的隐向量, 其shape为 batch_size x hidden_size
        if hidden_state is None:
            hidden_state = self.init_state(batch_size)
 
        # 循环执行RNN计算
        for step in range(seq_len):
            # 获取当前时刻的输入数据step_input, 其shape为 batch_size x input_size
            step_input = inputs[:, step, :]
            # 获取当前时刻的隐状态向量hidden_state, 其shape为 batch_size x hidden_size
            hidden_state = F.tanh(torch.matmul(step_input, self.W) + torch.matmul(hidden_state, self.U) + self.b)
        return hidden_state
 
# 初始化参数并运行
W_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.2], [0.1,0.2]]))
U_attr = torch.nn.Parameter(torch.tensor([[0.0, 0.1], [0.1,0.0]]))
b_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.1]]))
 
srn = SRN(2, 2, W_attr=W_attr, U_attr=U_attr, b_attr=b_attr)
 
inputs = torch.tensor([[[1, 0],[0, 2]]], dtype=torch.float32)
hidden_state = srn(inputs)
print("hidden_state", hidden_state)

运行结果：

Torch框架：

batch_size, seq_len, input_size = 8, 20, 32
inputs = torch.randn(size=[batch_size, seq_len, input_size])
 
# 设置模型的hidden_size
hidden_size = 32
paddle_srn = nn.RNN(input_size, hidden_size)
self_srn = SRN(input_size, hidden_size)
 
self_hidden_state = self_srn(inputs)
paddle_outputs, paddle_hidden_state = paddle_srn(inputs)
 
print("self_srn hidden_state: ", self_hidden_state.shape)
print("torch_srn outpus:", paddle_outputs.shape)
print("torch_srn hidden_state:", paddle_hidden_state.shape)

运行结果：

# 这里创建一个随机数组作为测试数据，数据shape为batch_size x seq_len x input_size
batch_size, seq_len, input_size, hidden_size = 2, 5, 10, 10
inputs = torch.randn(size=[batch_size, seq_len, input_size])
 
# 设置模型的hidden_size
bx_attr = torch.nn.Parameter(torch.tensor(torch.zeros([hidden_size, ])))
paddle_srn = nn.RNN(input_size, hidden_size)
 
 
# 获取paddle_srn中的参数，并设置相应的paramAttr,用于初始化SRN
W_attr = torch.nn.Parameter(torch.tensor(paddle_srn.weight_ih_l0.T))
U_attr = torch.nn.Parameter(torch.tensor(paddle_srn.weight_hh_l0.T))
b_attr = torch.nn.Parameter(torch.tensor(paddle_srn.bias_hh_l0))
self_srn = SRN(input_size, hidden_size, W_attr=W_attr, U_attr=U_attr, b_attr=b_attr)
 
# 进行前向计算，获取隐状态向量，并打印展示
self_hidden_state = self_srn(inputs)
paddle_outputs, paddle_hidden_state = paddle_srn(inputs)
print("torch SRN:\n", paddle_hidden_state.detach().numpy().squeeze(0))
print("self SRN:\n", self_hidden_state.detach().numpy())

运行结果：

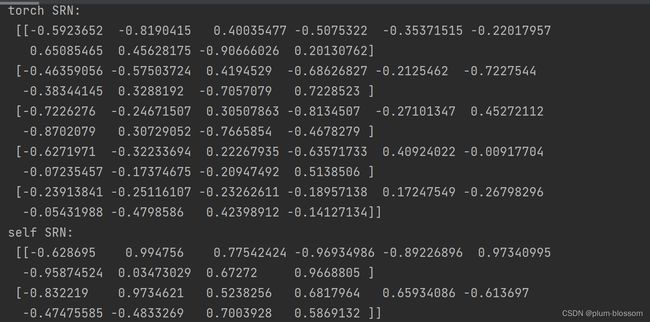
可以看到，两者的输出基本是一致的。另外，还可以进行对比两者在运算速度方面的差异。代码实现如下:

import time
 
# 这里创建一个随机数组作为测试数据，数据shape为batch_size x seq_len x input_size
batch_size, seq_len, input_size, hidden_size = 2, 5, 10, 10
inputs = torch.randn(size=[batch_size, seq_len, input_size])
 
# 实例化模型
self_srn = SRN(input_size, hidden_size)
paddle_srn = nn.RNN(input_size, hidden_size)
 
# 计算自己实现的SRN运算速度
model_time = 0
for i in range(100):
    strat_time = time.time()
    out = self_srn(inputs)
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    end_time = time.time()
    model_time += (end_time - strat_time)
avg_model_time = model_time / 90
print('self_srn speed:', avg_model_time, 's')
 
# 计算Paddle内置的SRN运算速度
model_time = 0
for i in range(100):
    strat_time = time.time()
    out = paddle_srn(inputs)
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    end_time = time.time()
    model_time += (end_time - strat_time)
avg_model_time = model_time / 90
print('torch_srn speed:', avg_model_time, 's')

运行结果：

可以发现，pytorch框架实现的SRN的运行效率显著高于自己实现的SRN效率。

6.1.2.3 线性层

线性层直接使用torch.nn.Linear算子。

6.1.2.4 模型汇总

在定义了每一层的算子之后，我们定义一个数字求和模型Model_RNN4SeqClass，该模型会将嵌入层、SRN层和线性层进行组合，以实现数字求和的功能.

# 基于RNN实现数字预测的模型
class Model_RNN4SeqClass(nn.Module):
    def __init__(self, model, num_digits, input_size, hidden_size, num_classes):
        super(Model_RNN4SeqClass, self).__init__()
        # 传入实例化的RNN层，例如SRN
        self.rnn_model = model
        # 词典大小
        self.num_digits = num_digits
        # 嵌入向量的维度
        self.input_size = input_size
        # 定义Embedding层
        self.embedding = Embedding(num_digits, input_size)
        # 定义线性层
        self.linear = nn.Linear(hidden_size, num_classes)
 
    def forward(self, inputs):
        # 将数字序列映射为相应向量
        inputs_emb = self.embedding(inputs)
        # 调用RNN模型
        hidden_state = self.rnn_model(inputs_emb)
        # 使用最后一个时刻的状态进行数字预测
        logits = self.linear(hidden_state)
        return logits
 
# 实例化一个input_size为4， hidden_size为5的SRN
srn = SRN(4, 5)
# 基于srn实例化一个数字预测模型实例
model = Model_RNN4SeqClass(srn, 10, 4, 5, 19)
# 生成一个shape为 2 x 3 的批次数据
inputs = torch.tensor([[1, 2, 3], [2, 3, 4]])
# 进行模型前向预测
logits = model(inputs)
print(logits)

运行结果：

6.1.3 模型训练

6.1.3.1 训练指定长度的数字预测模型

import os
import random
import torch
import numpy as np
from nndl import Accuracy, RunnerV3
 
# 训练轮次
num_epochs = 500
# 学习率
lr = 0.001
# 输入数字的类别数
num_digits = 10
# 将数字映射为向量的维度
input_size = 32
# 隐状态向量的维度
hidden_size = 32
# 预测数字的类别数
num_classes = 19
# 批大小
batch_size = 8
# 模型保存目录
save_dir = "./checkpoints"
 
# 通过指定length进行不同长度数据的实验
def train(length):
    print(f"\n====> Training SRN with data of length {length}.")
    # 固定随机种子
    np.random.seed(0)
    random.seed(0)
    torch.manual_seed(0)
 
    # 加载长度为length的数据
    data_path = f"D:/datasets/{length}"
    train_examples, dev_examples, test_examples = load_data(data_path)
    train_set, dev_set, test_set = DigitSumDataset(train_examples), DigitSumDataset(dev_examples), DigitSumDataset(test_examples)
    train_loader = torch.utils.data.DataLoader(train_set, batch_size=batch_size)
    dev_loader = torch.utils.data.DataLoader(dev_set, batch_size=batch_size)
    test_loader = torch.utils.data.DataLoader(test_set, batch_size=batch_size)
    # 实例化模型
    base_model = SRN(input_size, hidden_size)
    model = Model_RNN4SeqClass(base_model, num_digits, input_size, hidden_size, num_classes)
    # 指定优化器
    optimizer = torch.optim.Adam(model.parameters(), lr)
    # 定义评价指标
    metric = Accuracy()
    # 定义损失函数
    loss_fn = nn.CrossEntropyLoss()
 
    # 基于以上组件，实例化Runner
    runner = RunnerV3(model, optimizer, loss_fn, metric)
 
    # 进行模型训练
    model_save_path = os.path.join(save_dir, f"best_srn_model_{length}.pdparams")
    runner.train(train_loader, dev_loader, num_epochs=num_epochs, eval_steps=100, log_steps=100, save_path=model_save_path)
 
    return runner

6.1.3.2 多组训练

srn_runners = {}
lengths = [10, 15, 20, 25, 30, 35]
for length in lengths:
    runner = train(length)
    srn_runners[length] = runner

运行结果：

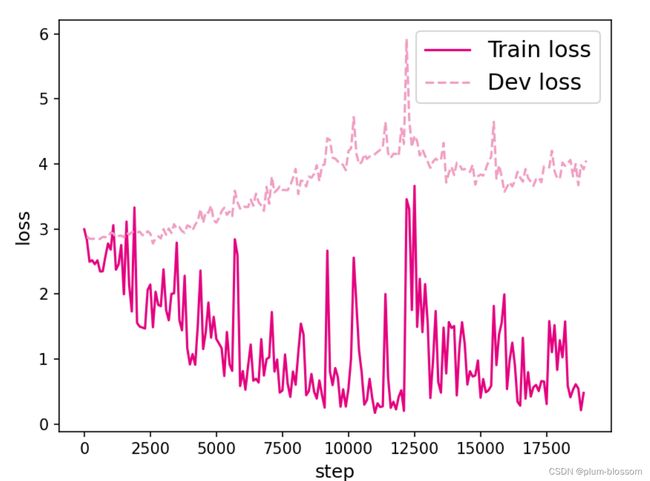
6.1.3.3 损失曲线展示

import matplotlib.pyplot as plt
def plot_training_loss(runner, fig_name, sample_step):
    plt.figure()
    train_items = runner.train_step_losses[::sample_step]
    train_steps = [x[0] for x in train_items]
    train_losses = [x[1] for x in train_items]
    plt.plot(train_steps, train_losses, color='#e4007f', label="Train loss")

    dev_steps = [x[0] for x in runner.dev_losses]
    dev_losses = [x[1] for x in runner.dev_losses]
    plt.plot(dev_steps, dev_losses, color='#f19ec2', linestyle='--', label="Dev loss")

    # 绘制坐标轴和图例
    plt.ylabel("loss", fontsize='large')
    plt.xlabel("step", fontsize='large')
    plt.legend(loc='upper right', fontsize='x-large')

    plt.savefig(fig_name)
    plt.show()

# 画出训练过程中的损失图
for length in lengths:
    runner = srn_runners[length]
    fig_name = f"./images/6.6_{length}.pdf"
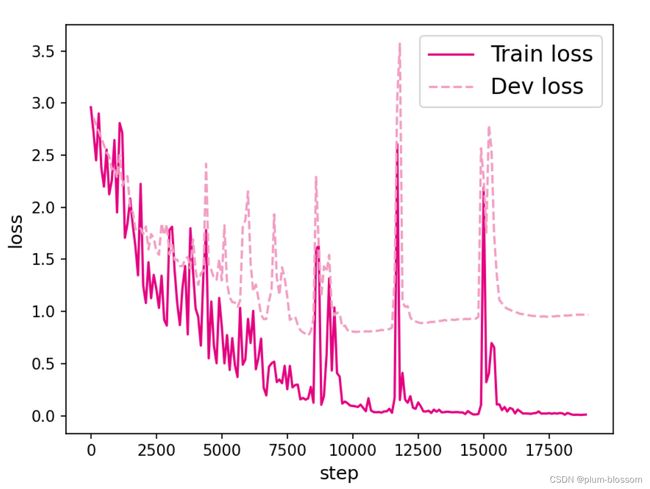
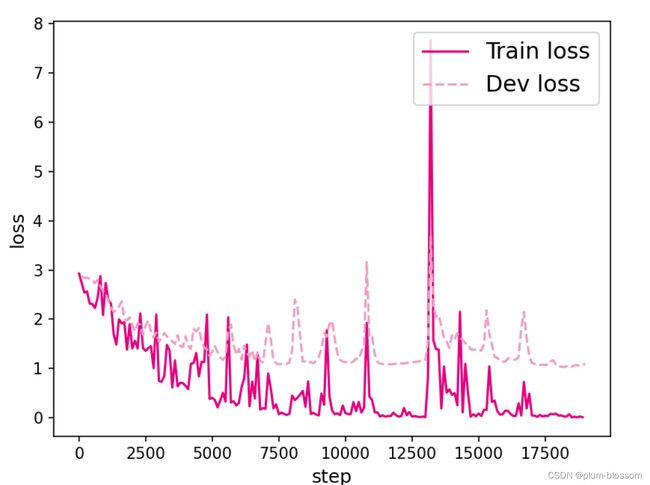
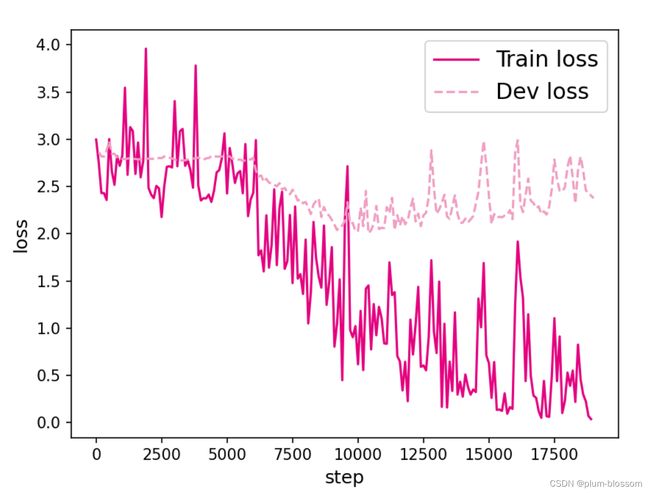
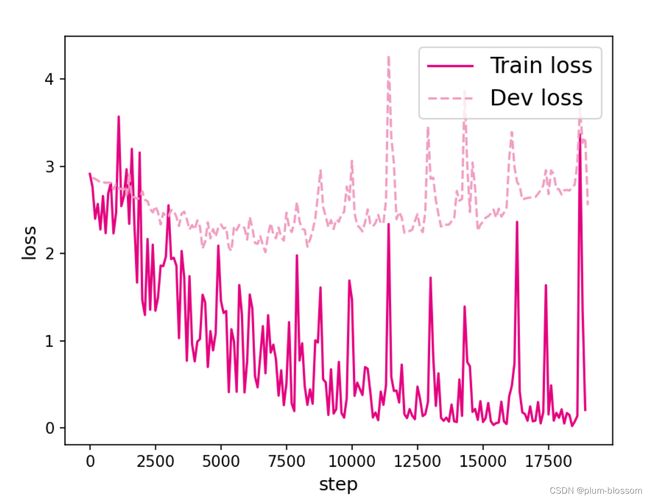
    plot_training_loss(runner, fig_name, sample_step=100)

运行结果：
k=10：

k=15:

k=20:

k=25:

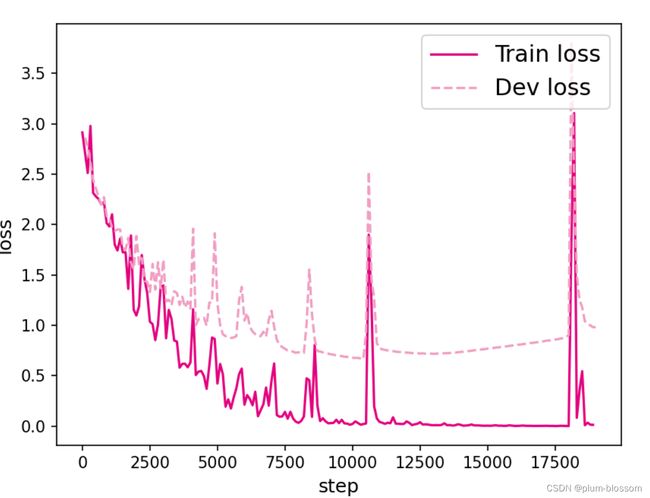
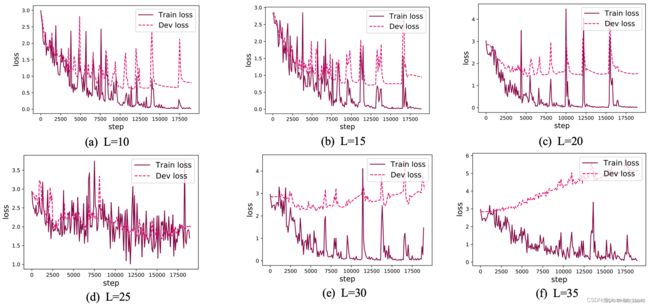
k=30:

k=35:

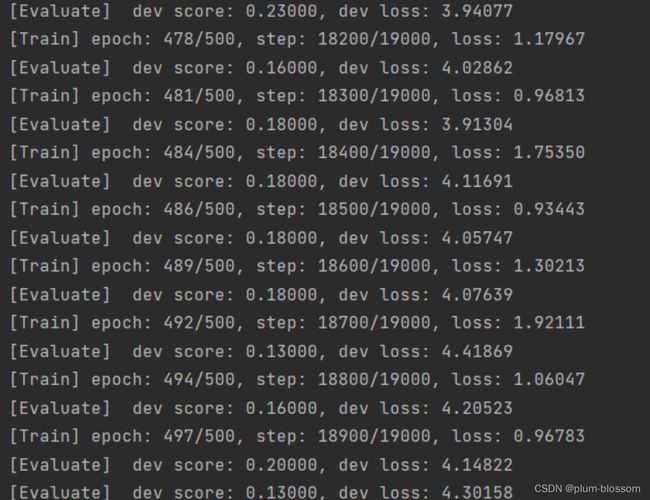
图6.6展示了在6个数据集上的损失变化情况，数据集的长度分别为10、15、20、25、30和35. 从输出结果看，随着数据序列长度的增加，虽然训练集损失逐渐逼近于0，但是验证集损失整体趋向越来越大，这表明当序列变长时，SRN模型保持序列长期依赖能力在逐渐变弱，越来越无法学习到有用的知识.

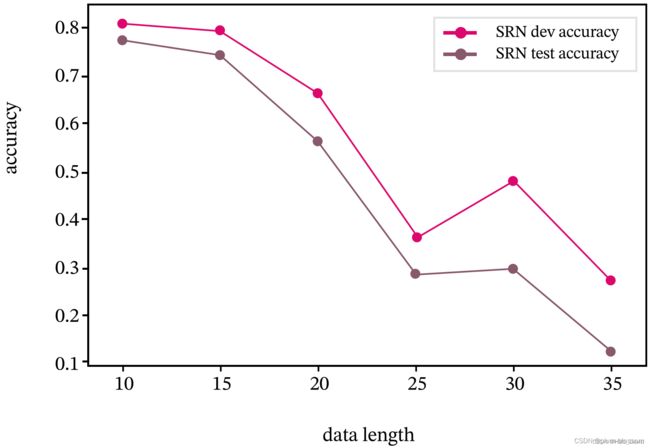
6.1.4 模型评价

srn_dev_scores = []
srn_test_scores = []
for length in lengths:
    print(f"Evaluate SRN with data length {length}.")
    runner = srn_runners[length]
    # 加载训练过程中效果最好的模型
    model_path = os.path.join(save_dir, f"best_srn_model_{length}.pdparams")
    runner.load_model(model_path)
 
    # 加载长度为length的数据
    data_path = f"D:/datasets/{length}"
    train_examples, dev_examples, test_examples = load_data(data_path)
    test_set = DigitSumDataset(test_examples)
    test_loader = torch.utils.data.DataLoader(test_set, batch_size=batch_size)
 
    # 使用测试集评价模型，获取测试集上的预测准确率
    score, _ = runner.evaluate(test_loader)
    srn_test_scores.append(score)
    srn_dev_scores.append(max(runner.dev_scores))
 
for length, dev_score, test_score in zip(lengths, srn_dev_scores, srn_test_scores):
    print(f"[SRN] length:{length}, dev_score: {dev_score}, test_score: {test_score: .5f}")
    import matplotlib.pyplot as plt
 
plt.plot(lengths, srn_dev_scores, '-o', color='#e4007f',  label="Dev Accuracy")
plt.plot(lengths, srn_test_scores,'-o', color='#f19ec2', label="Test Accuracy")
 
#绘制坐标轴和图例
plt.ylabel("accuracy", fontsize='large')
plt.xlabel("sequence length", fontsize='large')
plt.legend(loc='upper right', fontsize='x-large')
 
fig_name = "./images/6.7.pdf"
plt.savefig(fig_name)
plt.show()

总结

本次实验完成了循环神经网络的RNN记忆能力实验，构建数据集进行数据划分，构造Dataset类，构建了嵌入层、SRN层、线性层，从而最终得到模型，并且训练模型得到不同数据长度下的误差变化和可视化的损失曲线图，并对模型进行评价。

参考：

NNDL 实验6（上） - HBU_DAVID - 博客园 (cnblogs.com)

NNDL 实验6（下） - HBU_DAVID - 博客园 (cnblogs.com)