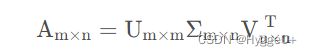机器学习|数学基础(二)
线性代数——特征值分解与奇异值分解
特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么,可以将每一个特征向量理解为一个线性的子空间,我们可以利用这些线性的子空间干很多的事情。不过,特征值分解也有很多的局限,比如说变换的矩阵必须是方阵。
奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性。就像是描述一个人一样,给别人描述说这个人长得浓眉大眼,方脸,络腮胡,而且带个黑框的眼镜,这样寥寥的几个特征,就让别人脑海里面就有一个较为清楚的认识,实际上,人脸上的特征是有着无数种的,之所以能这么描述,是因为人天生就有着非常好的抽取重要特征的能力,让机器学会抽取重要的特征,SVD是一个重要的方法。
【特征值分解】
特征值分解是将一个矩阵分解成下面的形式:A = Q∑Q-1
[符号含义]
其中Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角阵,每一个对角线上的元素就是一个特征值。
[特征值与特征向量]
一个向量α是方阵A的特征向量,将一定可以表示成形式 :Aα = λα,其中λ就被称为特征向量α对应的特征值,一个矩阵的一组特征向量是一组正交向量。
[几何意义]
一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。如果我们想要描述好一个变换,那我们就描述好这个变换主要的变化方向就好了。特征分解便是基于这样的思想。
根据特征值分解的式子,分解得到的Σ矩阵是一个对角阵,里面的特征值是由大到小排列的,这些特征值所对应的特征向量就是描述这个矩阵变化方向(从主要的变化到次要的变化排列),也就是提取出矩阵A的重要特征,我们利用这些变化方向结合它们的重要性就可以近似这个A矩阵变换。
【奇异值分解】
奇异值分解(Singular Value Decomposition,SVD)是线代中对于实数矩阵和复数矩阵的分解,将特征分解从正定矩阵(正定矩阵:如果对于所有的非零实系数向量 z,都有 z T A z > 0,则称矩阵A是正定的。正定矩阵的行列式必然大于0,所有特征值也必然 > 0。相对应的,半正定矩阵的行列式必然 ≥ 0)推广到任意 m × n矩阵。
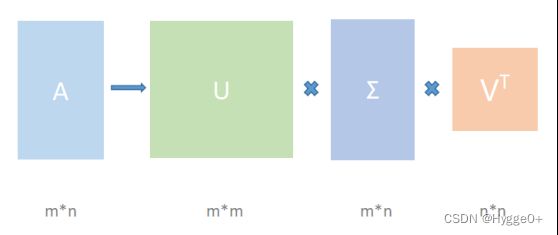
假设有 m × n 的矩阵 A,那么 SVD 就是要找到如下式的这么一个分解,将 A 分解为 3 个矩阵的乘积:(其中U、V都是正交矩阵。正交矩阵:若一个方阵其行与列皆为正交的单位向量,则该矩阵为正交矩阵,且该矩阵的转置和其逆相等。两个向量正交的意思是两个向量的内积为 0)
【奇异值分解求解方法】
U和V的列分别叫做 A的左奇异向量(left-singular vectors)和右奇异向量(right-singular vectors),Σ的对角线上的值叫做 A的奇异值(singular values)。
其实整个求解 SVD 的过程就是求解这 3 个矩阵的过程,而求解这 3 个矩阵的过程就是求解特征值和特征向量的过程,问题就在于 求谁的特征值和特征向量。
U的列由 A A T 的单位化过的特征向量构成。
V 的列由 A T A的单位化过的特征向量构成。
Σ 的对角元素来源于A A T 或 A T A的特征值的平方根,并且是按从大到小的顺序排列的。
知道了这些,那么求解 SVD 的步骤就显而易见了:
- 求 A A T的特征值和特征向量,用单位化的特征向量构成 U
- 求 A T A的特征值和特征向量,用单位化的特征向量构成 V
- 将 A A T 或者 A T A的特征值求平方根,然后构成 Σ
【截断奇异值分解】
奇异值σ跟特征值类似,在矩阵Σ中也是从大到小排列,而且σ的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,我们也可以用前r大的奇异值来近似描述矩阵:
r是一个远小于m、n的数,这样矩阵的乘法看起来像是下面的样子:
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵,r越接近于n,则相乘的结果越接近于A。而这三个矩阵的面积之和(在存储观点来说,矩阵面积越小,存储量就越小)要远远小于原始的矩阵A,我们如果想要压缩空间来表示原矩阵A,我们存下这里的三个矩阵:U、Σ、V就好了。
【特征值分解与奇异值分解的区别与联系】
特征值分解的目的和奇异值分解的目的是相同的,都是为了提取出矩阵最重要的特征。
特征值分解对应处理的只能是一个方阵,且特征值分布在对角线上;而奇异值分解是一个能适用于任意的矩阵的一种分解的方法,且对角线上的元素是奇异值(特征值的平方根)。
附参考链接:
奇异值分解 SVD 的数学解释_secsilm的博客-CSDN博客
特征值分解和奇异值分解 - gao_jian - 博客园 (cnblogs.com)