mt811

自由能计算专题3：gromacs计算自由能的7种方法案例

前言

本教程以甲烷在水中的溶剂化自由能和配体与受体蛋白质结合自由能为入门和进阶例子对使用分子动力学模拟方法来计算自由能的常见方法给出了示例，教程不会过多讲解各种计算自由能方法原理和分析原理，关于自由能计算原理和方法可以参考自由能专题1：原理及常见方法分析原理可以常考自由能专题2：计算与分析指南。该教程全部都经过本人的亲自的模拟和分析，确保无误，从实际操作出发，一步一步手动实现自由能的计算与分析，有助于理解自由能计算原理和结果分析。本教程主要采用GROMACS (5.1.4)分子动力学软件包来进行操作。以下案例的全部模拟配置文件均可在问末的链接中获得。

1.常见自由能计算方法和工具链

分子模拟计算自由能的方法众多，这里简单整理出一个表格，来展示本教程将要运用的自由能计算方法和后处理方法及相关的工具链。如下：

计算方法	后处理方法	自动实现分析工具/脚本
PMF	PMF(表达式)	图表数据处理工具

Umbrella Sampling(US:求解PMF)	WHAM,	gmx wham（gromacs自带） ,PLUMED,Colvars
	BAR	gmx bar(自带)，alchemical_analysis
	MBAR(0宽度的WHAM)	alchemical_analysis

FEP(Zwanzig)	DEXP	alchemical_analysis（下同）
	IEXP
	GINS
	GDEL
	BAR
	UBAR
	RBAR
	MBAR

TI(Kirkwood)	TI	alchemical_analysis
	TI-CUBIC

ＭＭ/PBSA		gmx_mm/pbsa（脚本）
		g_mm/pbsa（脚本）

Jarzynski Equality(Jarzynski)		gmx analyze（gromacs自带）
		alchemical_analysis
Metadynamics（MtD）		PLUMED
		Colvars

3.自由能计算实例

3.1 PMF：计算甲烷-甲烷之间的平均力势

在本教程中, 我将向您展示如何创建一个包含多个OPLS甲烷的系统, 将其置于TIP4PEW水盒子中, 并根据模拟所得信息计算甲烷-甲烷之间的平均力势.参考Barnett GROMACS教程3: 水中的多个甲烷,既然主题是计算自由能了，那么默认实操者能独立进行简单的分子模模拟任务，并熟知模拟流程，在这里关于模拟所需的三种重要基本配置文件（结构文件(.gro/.pdb), 拓扑文件(.itp,.top)和参数文件(.mdp).）如何创建就不再赘述了。这里会直接给出，只做简单的展示。（下同）

设置

甲烷的拓扑文件如下：

; Topology for methane in TIP4P

#include "oplsaa.ff/forcefield.itp"
#include "oplsaa.ff/tip4pew.itp"

[ moleculetype ]
; Name                       nrexcl
Methane                      3

[ atoms ]
;   nr       type  resnr residue  atom   cgnr     charge       mass  typeB    chargeB  massB
     1   opls_138      1   ALAB     CB      1     -0.240       12.011   
     2   opls_140      1   ALAB    HB1      2      0.060       1.008   
     3   opls_140      1   ALAB    HB2      3      0.060       1.008   
     4   opls_140      1   ALAB    HB3      4      0.060       1.008   
     5   opls_140      1   ALAB    HB4      5      0.060       1.008   



[ bonds ]
;  ai    aj funct            c0            c1            c2            c3
    1     2     1 
    1     3     1 
    1     4     1 
    1     5     1 

[ angles ]
;  ai    aj    ak funct            c0            c1            c2            c3
    2     1     3     1 
    2     1     4     1 
    2     1     5     1 
    3     1     4     1 
    3     1     5     1 
    4     1     5     1 

; water topology
[ system ]
; Name
Methane in water

[ molecules ]
; Compound             #mols
  Methane                10

1.首先, 将10个甲烷插入3.2 nm x 3.2 nm x 3.2 nm的盒子中:

$ gmx insert-molecules -ci methane.pdb -o box.gro -nmol 10 -box 3.2 3.2 3.2

2.溶剂化向盒子里加入1000个水分子

$ gmx solvate -cs tip4p -cp box.gro -o conf.gro -p topol.top -maxsol 1000

gmx solvate会自动更新topol.top

3.参数文件

以上过程的所有的文件均可以在1得到：关于PMF配置文件如下：

configura文件：模拟使用的gromacs5.1.4版本 
├── methane.pdb        :甲烷结构文件
├── box.gro            :步骤1生成的文件
├── conf.gro           :步骤2生成的文件
├── min1.mdp           :第一次能量最小化参数文件
├── min2.mdp           :第二次能量最小化
├── eql.mdp            :NVT 预平衡 
├── eql2.mdp           :NPT 预平衡
├── prd.mdp            :成品模拟，这里注意你可以改一下时长，我自己仅跑了5ns用于展示，建议跑100ns,rdf更平滑
├── topol.top          :拓扑文件，包含10个甲烷和1000个水分子
└── run_pmf.bsh        :自动化执行分子模拟流程的脚本

模拟

1.使用run_pmf.bsh脚本进行自动化模拟：

#1.给脚本赋予可执行的权限
$ chmod +x run_pmf.sh

#2.在当前目录下（configura）执行./run_pmf.bash脚本
$ ./run_pmf.sh

分析

1.让我们计算一下所谓的径向分布函数. 首先, 我们需要创建一个索引文件(index.ndx):

#以甲烷中的C原子代表整个分子
$ gmx make_ndx -f conf.gro
> a C
> q

2.计算甲烷-甲烷之间径向分布函数

$ gmx rdf -f prd.xtc -n index.ndx

然后选择 Group 6 “C” 两次，即选择两次6，Ctrl+d 计算生成rdf.xvg 文件

3.安装绘图工具gnuplot,在linux的ubuntu 系统安装：

#在终端输入以下命令自动安装：
$ sudo apt-get install gnuplot

4.绘制RDF(g®)图：

rdf曲线平滑依赖于你保存了多少帧, 运行了多长时间的模拟(原教程运行了100 ns, 保存了25k帧), 如果只是简单地绘制RDF, 得到的结果应该如下所示:（这里放原教程的图）

请注意, 它没有收敛到1. 我们多算了一个, 所以我们应该对其进行修正. 下面是gnuplot命令:

#1.在终端启动gnuplot
$ gnuplot

#2.进行修正:(我们有10个甲烷, 但计算RDF时只用了9个, 所以我们将g的值乘以N/(N-1), 即10/9. 它应该如下所示)
#输入>后面的代码即可
gnuplot> plot 'rdf.xvg' u 1:($2*10/9) w l

修正后的图像：

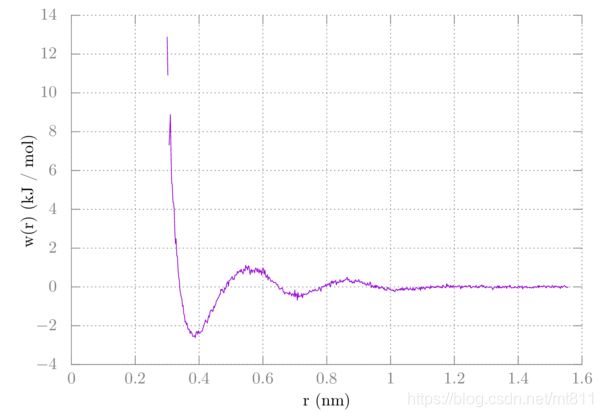
5.绘制甲烷-甲烷的平均力势（PMF）图：

现在, 要从甲烷-甲烷RDF中得到甲烷-甲烷之间的平均力势, 我们要计算：$ w=−kTln(g)w=−kTln⁡(g).$

因此, 要用gnuplot绘图, 请执行以下操作:

#1.在终端启动gnuplot
$ gnuplot

#2.绘制w(r)
gnuplot> plot 'rdf.xvg' u 1:(-8.314e-3*298.15*log($2*10/9)) w l

得到的图如下：

总结

注意到我们的抽样存在一个小的空白区. 这意味着, 在模拟中甲烷没有在那个距离有过相互作用. 我们将在后面的教程中使用伞形采样来解决这个问题。

3.2 Umbrella Sampling(US)：使用伞形采样计算甲烷-甲烷的PMF

在本教程中, 我们将使用窗口采样, 有时也称为伞状采样, 来计算甲烷-甲烷的平均力势PMF. 在教程1中, 我们通过模拟几个甲烷分子计算径向分布函数的方法直接获得了PMF. 像这样对几个溶质分子进行采样的方法并不总是可行的.

本教程参考gromacs官方伞形采样(GMX 5.0)和Barnett GROMACS教程5: 使用伞形采样计算甲烷-甲烷的平均力势PMF

模拟所需的甲烷分子拓扑文件如上，同这两个参考教程不同之处是，本教程使用更清晰文件组织来进行模拟，有利于初学者的学习。

设置

1.创建盒子

#将两个甲烷分子插入盒子中
$  gmx insert-molecules -ci methane.pdb -o box.gro -nmol 2 -box 3.2 3.2 3.2

2.溶剂化

$ gmx solvate -cs tip4p -cp box.gro -o conf.gro -p topol.top

3.创建索引文件：

我们还需要创建一个索引文件, 其中包含我们感兴趣的两个组, 它们之间受伞形势限制. 使用gmx make_ndx创建一个索引文件, 其中包含每个甲基碳的组, 并将其分别命名为CA和CB.

$ gmx make_ndx -f conf.gro
>  splitres  2         #本人操作是时CH4残基在组2，总之选择CH4残基所在组即可，将残基开成两个CH4（6和7）
> 6 & a C      #单独取出两个甲烷分子中的C原子（下同） 生成 8
> 7 & a C     #生成 9
> name 8 CA    #重命名 8 （下同)
> name 9 CA
>q             #保存退出 ，生成index.ndx索引文件

使用gmx make_ndx的其他方法同样可以达到目的. 关键是, 需要将每个甲烷的碳原子放在单独的索引组中, 并分别将它们命名为CA和CB.

4.参数文件

我们在很大程度上重复使用前一个教程（PMF）中的参数文件, 但是我们将添加一个与质心(COM)牵引有关的部分. 牵引代码可以将甲烷维持在指定距离。可能有几种不同的设置方法, 但对于这个系统, 我们将手动指定两个甲烷间的距离.我们将在一般模拟时所需要的所有mdp运行控制文件（能量最小化，npt和nvt预平衡，成品模拟mdp文件）（如1教程 PMF）中添加以下代码：

;{ US采样代码：质心牵引
;===============================================================================
pull                  = Yes ; Yes/No  使用牵引代码
pull-ngroups          = 2   ; 牵引组数目,这里是CA和CB两个
pull-ncoords          = 1   ; 只沿一个坐标方向进行牵引
pull-group1-name      = CA ; 牵引组名称, 来自top或ndx；.对我们来说,
                      ; 这是其中一个甲烷的碳, 尽管我们也可以选择整个甲烷.
                      ;如果那样做的话, 就会沿着两个甲烷分子的质心方向进行牵引
pull-group2-name      = CB         ;另一个甲烷的碳原子
pull-coord1-type      = umbrella
                      ; umbrella:简谐势
                      ; constraint:刚性约束
                      ; constant-force:恒力, 无须pull-init和pull-rate
pull-coord1-geometry  = distance
                      ; distance:沿质心间的矢量, 用pull-dim选择分量
                      ; direction:沿pull-vec方向
                      ; direction-periodic:同direction, 但距离可超过盒长一半. 使用时盒子在牵引方向不能变  化
                      ; cylinder:圆柱

pull-coord1-groups    = 1 2   ; 对此坐标牵引的两个组(定义见后面). 实际上你可以定义                       
                          ;更多的牵引坐标, 也可以在不同的分子组之间进行牵引, 但我们在这里不使用这些选项
                      
pull-coord1-rate      = 0.0   ; 速率(nm/ps)
                      ;我们不需要两个组沿坐标方向运动, 因此设置为零
                      
pull-coord1-k         = 5000.0   ; 力常数(kJ/mol-nm^2)
pull-coord1-init      = WINDOW     ; 零时刻的基准距离,这是个变量
                             ;两个组的初始间距. 这是关键字, 我们将使用bash脚本将其替换为每个窗口的相应值
pull-coord1-start     = no   ; No:不修改pull-init; Yes:将初始构型的质心距离添加到pull-init       
                             ;我们手动指定每个窗口的距离, 因此计算时不需要考虑质心距离
;}==============================================================================

5.生成构型文件

为了运行伞形采样, 我们必须沿反应坐标 ζ 生成一系列构型. 其中的一些构型将作为伞形采样窗口的初始构型, 并进行独立的模拟. 下图解释了这些原则. 图的上部显示了我们将要运行的牵引模拟, 目的在于产生一系列沿反应坐标的构型, 模拟完成后会抽取这些构型(图片上部和中部之间的虚线箭头). 图的中部对应着每一采样窗口内的独立模拟, 其中使用伞形偏离势将自由甲烷的质心限制在窗口中. 图的底部展示了构型直方图的理想结果, 相邻窗口存在重叠, 这样以后就可以从这些模拟得到连续的能量函数.

对本教程的例子, 反应坐标为单一方向. 为产生这些构型, 我们必须牵引甲烷CA, 使其远离甲烷CB.我们模拟了26个窗口, 距离从0.05 nm到大约1.3 nm. 请注意, 我为每次模拟都添加了牵引力输出文件选项-pf和牵引距离输出文件选项-px. 这是因为使用-deffnm选项时GROMACS会覆盖这两个文件. 此外, 我使用-n指定了索引文件, 因为gmx grompp需要获取我们使用牵引参数指定的组。

对于其他体系, 保存构型的频率可能需要更高或者更低, 只要足够就好. 关键是沿反应坐标获得足够的构型, 以使伞形采样窗口的间距正常, 窗口间距以甲烷CA和CB的质心(用C来代替了)距离表示, 其中CB为参考组.

由于我们需要为26个窗口进行独立的模拟，那么就需要27份模拟所需要的配置文件，但是我们将使用脚本来简单地更新参数文件模板中的适当值（pull-coord1-init）, 因此实际上只需要为模拟过程的每个部分提供一个模板。以上过程所需及生成的文件从1可以获得，其配置文件结构如下：

**configura 文件下的目录结构**
├── collect_dat.sh              :批量收集分析所需要数据的脚本
├── batche.sh                   :批量执行job0.sh -->job26.sh 的脚本
├── write_mdp.sh                :批量生成mdp文件的脚本，主要修改mdp 中的pull-coord1-init=WINDOWS 的值
├── write_sh.sh                :批量生成job文件的脚本,主要修改job文件中 WINDOW=Wnum的值，
├── job.sh                      :为每一窗口独立运行整个模拟过程（EM->NVT->NPT->PRD），即WINDOW0，
├── MDP                         :总运行参数mdp文件夹
│   ├── EM                      :能量最小化参数mdp文件夹
│   │   ├── 1em.mdp             :第1次能量最小化参数mdp模板文件
│   │   ├── 2em.mdp             :第2次能量最小化参数mdp模板文件
│   │   └── write_mdp.sh        : 用法：./write_mdp.sh  1em     即可后接mdp文件前缀  ./write_mdp.sh  2em
│   ├── NVT                     :等温等容预平衡参数mdp文件夹
│   │   ├── nvt.mdp             :等温等容预平衡参数mdp模板文件
│   │   ├── write_mdp.sh        : 用法：./write_mdp.sh  nvt     即可后接mdp文件前缀
│   ├── NPT                     :等温等压预平衡参数mdp文件夹
│   │   ├── npt.mdp             :等温等压预平衡参数mdp模板文件
│   │   └── write_mdp.sh        : 用法：./write_mdp.sh  npt     即可后接mdp文件前缀
│   └── PRD                     :成品模拟参数mdp文件夹
│       ├── prd.mdp             :成品模拟参数模板mdp文件
│       └── write_mdp.sh        : 用法：./write_mdp.sh  prd     即可后接mdp文件前缀
├── Methane                     :结构文件和拓扑文件夹
│   ├── box.gro                 :10个甲烷盒子结构文件
│   ├── conf.gro                :模拟体系结构文件10个甲烷+水
│   ├── index.ndx               :甲烷中所有原子的索引文件
│   ├── methane.pdb             :甲烷结构文件
│   └── topol.top               :体系top文件
└── REDERME.md

5.1.使用write_mdp.sh脚本在文件夹EM/NVT/NPT/PRD下分别生成0到26个.mdp文件

脚本如下:

#!/bin/bash
#对于模拟, 我们将使用shell脚本替换.mdp文件中的WINDOW关键字
# 打开一个通用的.mdp文件，并替换以下值
#26个窗口, 距离从0.05 nm到大约1.3 nm.既WINDOW有27个值，增量为0.05
for ((i=0;i<27;i++))
do

# 小数点前补0
x=$(echo "0.05*$(($i+1))" | bc |awk '{printf "%.2f",$0}');

sed 's/WINDOW/'$x'/g' $1.mdp  >$1$i.mdp

done

使用示例：例如在./configura/MDP/EM下批量生成1em.mdp和2em.mdp各27份

#给脚本赋予可执行权限
$chmod +x write_mdp.sh

#批量生成27份1em.mdp文件
$ ./write_mdp.sh 1em

#批量生成27份2em.mdp文件
$ ./write_mdp.sh 2em

接下来以上述方式生成整个模拟所需要的mdp文件(同上)

模拟

1.对于每一个独立窗口我们可以用脚本（job.sh）进行自动化的模拟整个过程如下：

#!/bin/bash

# 设置一些环境变量，即你所有模拟配置文件所在的根目录（里面包括MDP，Methane,.sh脚本，在命令行使用pwd即可获得）
#"/home/eric/free_energy/04.US/configura" 即为我所有模拟配置文件所在根目录
FREE_ENERGY=/home/eric/free_energy/04.US/configura

echo "Free energy home directory set to $FREE_ENERGY"

MDP=$FREE_ENERGY/MDP
echo ".mdp files are stored in $MDP"

#Wnum 为窗口数，将会被write_sh.sh进行批量替换成27个不同的值
WINDOW=Wnum

# 将为WINDOW的每个值和工作流程中的每个步骤创建一个新的目录，以实现最大限度的组织。

mkdir Window_$WINDOW
cd Window_$WINDOW

#################################
# 能量最小化第1步:STEEP  #
#################################
echo "Starting minimization for Window = $WINDOW..." 

mkdir EM_1 
cd EM_1

# Iterative calls to grompp and mdrun to run the simulations

gmx grompp -f $MDP/EM/1em$WINDOW.mdp -c $FREE_ENERGY/Methane/conf.gro -p $FREE_ENERGY/Methane/topol.top -n $FREE_ENERGY/Methane/index.ndx -o min$WINDOW.tpr -maxwarn 1 

gmx mdrun -nt 2 -v -deffnm min$WINDOW -pf pullf-min$WINDOW -px pullx-min$WINDOW

sleep 10

#################################
# 能量最小化第 2步: STEEP #
#################################

cd ../
mkdir EM_2
cd EM_2 

#我们在这里使用了 -maxwarn 1，因为 grompp 错误地抱怨使用了一个普通的截止值。
# 这是一个小问题，将在未来的Gromacs版本中得到修正。
gmx grompp -f $MDP/EM/2em$WINDOW.mdp -c ../EM_1/min$WINDOW.gro -p $FREE_ENERGY/Methane/topol.top -n $FREE_ENERGY/Methane/index.ndx -o min$WINDOW.tpr -maxwarn 1

gmx mdrun -nt 2 -v -deffnm min$WINDOW -pf pullf-min$WINDOW -px pullx-min$WINDOW

echo "Minimization complete."

sleep 10

#####################
# NVT 等容平衡 #
#####################
echo "Starting constant volume equilibration..."

cd ../
mkdir NVT
cd NVT

gmx grompp -f $MDP/NVT/nvt$WINDOW.mdp -c ../EM_2/min$WINDOW.gro -p $FREE_ENERGY/Methane/topol.top -n $FREE_ENERGY/Methane/index.ndx -o nvt$WINDOW.tpr  -maxwarn 1


gmx mdrun -nt 2 -v -deffnm nvt$WINDOW -pf pullf-nvt$WINDOW -px pullx-nvt$WINDOW


echo "Constant volume equilibration complete."

sleep 10

#####################
# NPT 等压平衡 #
#####################
echo "Starting constant pressure equilibration..."

cd ../
mkdir NPT
cd NPT

gmx grompp -f $MDP/NPT/npt$WINDOW.mdp -c ../NVT/nvt$WINDOW.gro -p $FREE_ENERGY/Methane/topol.top -n $FREE_ENERGY/Methane/index.ndx  -t ../NVT/nvt$WINDOW.cpt -o npt$WINDOW.tpr -maxwarn 1

gmx mdrun -nt 2 -v -deffnm npt$WINDOW -pf pullf-npt$WINDOW -px pullx-npt$WINDOW


echo "Constant pressure equilibration complete."

sleep 10

#################
# 成品模拟 MD #
#################
echo "Starting production MD simulation..."

cd ../
mkdir Production_MD
cd Production_MD

gmx grompp -f $MDP/PRD/prd$WINDOW.mdp -c ../NPT/npt$WINDOW.gro -p $FREE_ENERGY/Methane/topol.top -n $FREE_ENERGY/Methane/index.ndx  -t ../NPT/npt$WINDOW.cpt -o prd$WINDOW.tpr -maxwarn 1

gmx mdrun -nt 2 -v -deffnm prd$WINDOW -pf pullf-prd$WINDOW -px pullx-prd$WINDOW

echo "Production MD complete."

# End
echo "Ending. Job completed for Window= $WINDOW"

2.对于以上脚本你仅需要修改：FREE_ENERGY=/home/eric/free_energy/04.US/configura 中的“/home/eric/free_energy/04.US”部分。这一部分为你配置文件configura所在根目录，每个人都是不一样的。

3.以上只是一个独立窗口的完整的模拟脚本，而我们需要模拟27次，即需要下列脚本（write_sh.sh ）批量生成27个job.sh脚本：

#!/bin/bash

#对于模拟, 我们将使用shell脚本替换.job文件中的Wnum关键字

# 打开一个通用的job.sh文件，并替换Wnum的值

#26个窗口, 即Wnum有26个值，从0到26
for ((i=0;i<27;i++))
do
sed 's/Wnum/'$i'/g' $1.sh  >$1$i.sh
done

准备工作全部做完后如下开始进行27个窗口独立的模拟，使用一个简单脚本（ batche.sh）批量自动化这一过程如下：

#!/bin/bash
#批量执行job脚本,这里0时已经被测式执行来。从1开始
#给新生成的26个Job脚本赋予可执行的权限
chmod +x job*.sh
for num  in {0..26}
do
./job$num.sh
done

5.开始模拟

#1.赋予脚本执行权限
$ chmod +x batche.sh

#2.开始全部的模拟（共27,这里只是用单机电脑来跑的，如果使用集群可以27个任务并行运行，出结果更快）本机4核8线程差不多三天完成。
$ ./batche.sh

分析

1.正常模拟结束将会产生27个Window_0 到Window_27文件夹，该文件夹内容如下，以Window_0为例：

├── Window_0                         
│   ├── EM_1                      
│   │   ├── min0.gro                    
│   │   └── ....
│   ├── EM_2
│   │   ├── min0.gro                    
│   │   └── ....
│   ├── NVT                           
│   │   ├──nvt0.gro
│   │   └── .....
│   ├── NPT                     
│   │   ├── npt0.gro             
│   │   └── .....   
│   └── PRD                    
│       ├── prd0.gro
│       ├── prd.tpr                 ;分析所需文件      
│       ├── pullf-prd0.xvg          ;分析所需文件  
│       └── ....

2.收集26个窗口，即27份独立的模拟成品模拟文件，使用一个简单脚本(collect_dat.sh)将27Window文件夹下的数据收集起来如下：

#!/bin/bash
#创建保存分析需要用的prd0.tpr 到prd26.tpr 和 pullf-prd0.xvg 到pullf-prd26.xvg文件的文件夹 analysis_us  
mkdir analysis_us
cd analysis_us
for num  in {0..26}
do

cp ../Window_$num/Production_MD/prd$num.tpr ./
cp ../Window_$num/Production_MD/pullf-prd$num.xvg ./

done

3.我们将使用gmx wham来获取PMF. 该程序接受一个包含.tpr文件列表的文件和另一个包含.xvg文件列表的文件, 后者中包含了输出的牵引力.要创建这两个文件列表的文件, 在analysis_us文件夹下执行以下命令：

$ ls prd.*.tpr > tpr.dat
$ ls pullf-prd.*.xvg > pullf.dat

4.使用GROMACS实现的加权直方图分析(WHAM)来重建PMF：

$ gmx wham -it tpr.dat -f pullf.dat

运行gmx wham之后, 平均力势的计算结果保存在名为profile.xvg的文件中. 绘图应该如下所示:

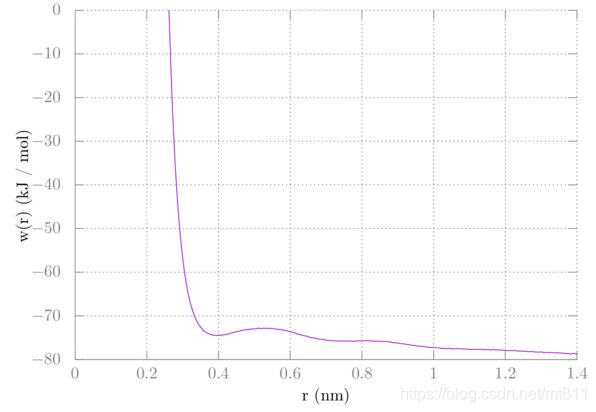
5.图像修正

我们希望在较远的距离处相互作用为零. 但是, 由于我们使用了三维的偏置势, 需要进行校正. 想象一下将其中一个甲烷作为参考点. 另一个甲烷可以在该点周围距离 r处进行采样, 覆盖了半径为 rr的某个球体的表面. 这为我们的采样增加了额外的构型空间, 降低了熵. 需要消除这些额外熵对PMF的贡献. 回想一下, 等温等压系综中的吉布斯自由能是 −kTln(W), 其中 W 为分配函数. 对我们的情况, 甲烷绕着球体表面采样时, w 与该球体的表面积成正比. 因此, 需要增加 2kTln® 的校正. 此外, 我们需要将图形向上移动, 使其尾部变为零. 对我的结果需要增加的数值大约为7, 但你需要增加的数值可能不同. 要在gnuplot中绘制此图, 请在gnuplot终端中执行以下操作:

#1.在终端启动gnuplot
$ gnuplot

#2.进行修正:输入>后面的代码即可
gnuplot> plot 'profile.xvg' u 1:($2+2*8.314e-3*298.15*log($1)+77) w l

您的PMF现在应该如下所示:

总结

与教程1中的PMF相比, 可以看到它们几乎相同:

区别在于, 使用教程3的直接方法, 采样不可能接近窗口采样. 两个甲烷不会自然地相互靠近, 这就是为什么我们必须增加伞形势以维持它们之间距离的原因。

另一个输出是histo.xvg, 它有助于确定窗口之间是否有足够的重叠. 以下是我模拟的每个直方图的绘图:

很显然, 我们的窗口已经足够重叠了. 否则的话, 我们可能必须选择较小的窗口, 或选择缺少模拟的特定点进行模拟.

3.3 FEP:计算甲烷在水中的溶剂化自由能

该教程在网上三个类似的教程，笔者在这里先简单例举出来，然后再说明这些教程的异同，和参考这些教程哪些内容

参考教程链接参考内容
教程1：gromacs 官方教程6：自由能计算流程，分析方法(bar)
教程2：译：自由能计算: 水中的甲烷(GMX 5.0) 与教程1其他都相同，算升级版，多分析了两组数据
教程3：译：Barnett GROMACS教程4: 甲烷的溶剂化自由能使用python脚本对自由能计算方法自动化分析

教程3和教程（1和2）不同之处有四点：

一是前者使用水模型同3.1和3.2一样是TIP4P,而后者是TIP3P；

二是前者在描述自由能的变化时考虑了范德华和静电相互作用，而后者只考虑范德华相互作用；

三是前者使用分析自由能的方法不同，前者是TI,后者是使用了gromacs自带的BAR后处理方法;

四是前者只进行了15次独立模拟，后者进行21次独立模拟。

根据FEP和TI计算原理可知，使用分子模拟计算自由能时都是通过多个 $\lambda$ 值控制不同相互作用类型的进度来处理自由能计算，因此这样就可以分别控制库仑、LJ和约束变换等自由能计算，所以无论使用FEP和TI那一种计算方法，在gromacs它们使用的都是同一套自由能计算代码，只是对自由能的后处理分析不同而已。

本教程主要基于教程（1和2）模拟设置进行模拟，，将指导用户计算一个简单的自由能变化, 中性甲烷与一盒子水之间范德华相互作用的去耦合(即移除)，并使用gromacs自带工具和python分析工具（alchemical_analysis）中基于FEP计算自由能的8种后处理方法来简要分析这一过程中自由能的变化，会涉及相关工具的使用和安装。

体系从状态A转变到状态B过程的自由能变化 $\Delta G_{AB}$ 是耦合参数 $\lambda$ 的函数, 它代表了状态A和B之间转变的程度, 也就是哈密顿量的微扰程度以及体系已经变化的程度. 利用不同 $\lambda$ 对应的模拟可以绘制 $\partial H/\partial \lambda$ 曲线, 并由此得到 $\Delta G_{AB}$ 自由能计算的第一步是确定使用多少个点描述从状态A( $\lambda$ = 0)到状态B( $\lambda = 1$ )的转变, 其目的在于收集足够多的数据, 完全充分地对相空间进行取样, 并得到合理的 $\partial H/\partial \lambda$ 曲线:

如上图所示，状态A是在水中完全相互作用的甲烷. 状态B将是一个甲烷被隐去, 表示它与水的所有范德华相互作用和库仑相互作用（本例只考虑范德华力）都被关闭; 甲烷可以与自身相互作用, 水可以与自身相互作用, 但甲烷和水不会相互作用. 就好像我们将甲烷从水中取出并置于真空中, 而在其他地方我们仍然拥有甲烷所在的水. 我们总共有21个状态。

设置

1.准备甲烷的拓扑文件:注意此模拟使用的TIP3P水模型

; Topology for methane in TIP3P

#include "oplsaa.ff/forcefield.itp"

[ moleculetype ]
; Name                       nrexcl
Methane                      3

[ atoms ]
;   nr       type  resnr residue  atom   cgnr     charge       mass  typeB    chargeB  massB
     1   opls_138      1   ALAB     CB      1      0.000       12.011   
     2   opls_140      1   ALAB    HB1      2      0.000       1.008   
     3   opls_140      1   ALAB    HB2      3      0.000       1.008   
     4   opls_140      1   ALAB    HB3      4      0.000       1.008   
     5   opls_140      1   ALAB    HB4      5      0.000       1.008   



[ bonds ]
;  ai    aj funct            c0            c1            c2            c3
    1     2     1 
    1     3     1 
    1     4     1 
    1     5     1 

[ angles ]
;  ai    aj    ak funct            c0            c1            c2            c3
    2     1     3     1 
    2     1     4     1 
    2     1     5     1 
    3     1     4     1 
    3     1     5     1 
    4     1     5     1 

; water topology
#include "oplsaa.ff/tip3p.itp"

[ system ]
; Name
Methane in water

[ molecules ]
; Compound             #mols
Methane                1
SOL                    596

你会注意到, 所有的电荷都设置为零. 这种设置有一个实际的原因, 正常情况下, 在关闭范德华相互作用之前, 会先关闭溶质与水之间的电荷相互作用. 如果仅仅保留电荷相互作用而关闭了Lennard-Jones项, 正负电荷相互接近的距离可能无限小, 导致体系非常不稳定, 并可能崩溃. 本教程的步骤基本假定在此之前已经正确地关闭了电荷项, 我们将只关闭溶质与溶剂分子之间的范德华相互作用.这一点下面在设置自由能计算参数（couple-lambda0 ）会提到。

2.参数文件：

同教程3.2.US类似，只是我们添加的是一个计算自由能部分而前者是伞形拉伸的部分, 以便慢慢关闭甲烷与水的相互作用。

另外, 我们还需要为每个 $\lambda$ 状态的准备独立模拟所必备的基本配置文件. 我们需要21个最小化, 21个预平衡,21个成品模拟等的参数文件. 但是我们将使用脚本来简单地更新参数文件模板中的适当值（init_lambda_state ）, 因此实际上只需要为模拟过程的每个部分提供一个模板。

以em_steep.mdp模板为例：（前部分为一般模拟所学控制参数，请重点关注自由能计算部分控制参数！！！）

; ;{ 预处理, 使用 C++ 语法
;===============================================================================
include =          ; 含引用文件的目录, 拓扑文件中可引用其中的文件, 可多项
                   ; 例: -I/home/joe/joy -I/home/tom/tim -IC:/GMX/top
define                  =  -DFLEXIBLE
                         ; 预定义, 默认无, 可多项, 区分大小写
                         ; -DPOSRES:   使用位置限制文件进行位置限制动力学模拟
                         ; -DFLEXIBLE: 启用柔性水, steep效果更好, cg, l-bfgs或简正分析须开启
;}==============================================================================


;{ 能量最小化运行控制
;===============================================================================
integrator               = l-bfgs   ;能量最小化方法, steep:最陡下降; cg:共轭梯度; lbfgs:二次收敛
nsteps                   = 5000     ; 最大积分步数, 默认0, -1:无限制
emtol                    = 100      ; 力的最大容差(kJ/mol-nm), 对壳层值应小于1
emstep                   = 0.01     ; 初始步长(nm)
nbfgscorr                = 10       ; L-BFGS最小化的校正步数
;}==============================================================================


;{ 壳层动力学
;===============================================================================
niter                    = 20       ; 优化壳层位置和柔性约束的最大迭代次数
;}==============================================================================


;{ 输出控制
;===============================================================================
nstlog                   = 1        ; 日志文件输出频率
nstenergy                = 1        ; 能量文件输出频率
;}==============================================================================



;{ 邻区搜索
;===============================================================================
cutoff-scheme            = verlet   ; 截断方式, Verlet:粒子截断; Group:电荷组
nstlist                  = 1        ; 邻区列表更新频率, 0:真空模拟; -1:自动
ns_type                  = grid     ; 邻区搜索算法, Grid:较快; Simple:仅与Group联用
rlist                    = 1.2      ; 邻区列表截断距离(nm)
rcoulomb                 = 1.2      ; 静电截断半径, 不超过最小盒子边长一半
rvdw                     = 1.2       ; 范德华截断半径
;}==============================================================================


;{ 周期性
;===============================================================================
pbc                     = XYZ    ; 周期性边界条件, XYZ; XY; No:忽略盒子, 截断与nstlist置零
;}==============================================================================


;{ 静电与范德华
;===============================================================================
; Electrostatics
coulombtype              = PME   ; 静电计算方法
; van der Waals
vdwtype                  = cutoff ; 范德华计算方法
vdw-modifier             = potential-switch ;   ;修正方法
rvdw-switch              = 1.0    ;从何时开始切换LJ力或势能，只适用与对力或势能切换的情况
DispCorr                  = EnerPres  ; 长程色散校正, No:无; Ener:能量; EnerPres:能量和压力
;}==============================================================================


;{ EWALD/PME/PPPM
;===============================================================================
fourierspacing           = 0.12   ;PME/PPPM方法FFT格点最大间距(nm)
pme_order                = 6      ;内插阶数, 默认4相当于三次插值
ewald_rtol               = 1e-06  ; 静电能量容差
epsilon_surface          = 0      ; 偶极校正
;}==============================================================================

;{ 温度和压力耦合，在能量最小化时被关闭，可以不写此参数
;===============================================================================
tcoupl                   = no
pcoupl                   = no
;}==============================================================================

;{ 初始速度 ，能量最下化时没有速度，该参数可不写
;===============================================================================
gen_vel                  = no 
;}==============================================================================

;{ 键约束
;===============================================================================
constraints              = none     ;      None:仅拓扑中指定的约束 L-BFGS 在此不能使用约束
                                    ;   h-bonds:含氢键;   h-angles:含氢键和键角
                                    ; all-bonds:所有键; all-angles:所有键和键角
constraint-algorithm     = lincs    ; 约束算法, Lincs:不支持键角; Shake:慢且不稳定, 不支持EM和dd
continuation             = no       ; 是否约束初始构型, 并重置壳层
lincs-order              = 12       ; 约束耦合矩阵展开的最高阶数


;{ 自由能计算
;===============================================================================
free_energy              = yes    ; No/Yes/Expand，表示进行自由能计算, 将会进行所选分子(下面定义)从状态A到状态B的内插
init_lambda_state        = nlambda     ;向量的一个索引号(始于0),它只是一个整数的占位符,我们将模拟21个不同                                       ;的状态, 因此这个数字的范围是0到20.
                                       ;我们的脚本会将其替换为每个状态相应的值(0,,,20)
delta_lambda             = 0         ; 每步的增量, 慢增长方法取非零值
calc_lambda_neighbors    = -1        ;相邻的数目. bar取1, mbar取-1,教程1和2都是取1，这里我们需要使用mbar
                                     ;就取-1了，方便我们使用所有分析方法，一站式处理。
;此处指定的lambda矢量,每一个组合都是一个索引，从init_lambda_state中为每一个模拟检索。
; init_lambda_state        0    1    2    3    4    5    6    7    8    9    10   11   12   13   14   15   16   17   18   19   20
vdw_lambdas              = 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00       ;用于范德华相互作用转变的 λ 值的数组
coul_lambdas             = 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00       ;用于库伦(静电)相互作用转变的 λ 值的数组

;我们不会改变任何键合或约束的相互作用。
bonded_lambdas           = 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00       ;用于键合相互作用转变的 λ 值的数组
restraint_lambdas        = 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00       ;用于限制相互作用转变的 λ 值的数组

;质量不变（lambda=0和lambda=1时粒子特性相同）。
mass_lambdas             = 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00       ;用于原子质量转变的 λ 值的数组; 当转变分子的化学本质时会使用.

;温度不变，这里不做模拟退火
temperature_lambdas      = 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00       ;用于温度转变的 λ 值的数组; 仅用于模拟退火

; 解耦选项
sc-alpha                 = 0.5   ;“软核”Lennard-Jones方程中使用的 α 缩放因子的值
sc-coul                  = no       ; 线性地转变库伦相互作用. 这是默认行为, 给出是为了更清楚
sc-power                 = 1      ;软核方程中 λ 的次数
sc-sigma                 = 0.3       ;对C6或C12参数为0, 或者 σ < sc-sigma(典型为H原子)的任意原子类型, 赋给 σ 的值
couple-moltype           = Methane  ; 耦合的分子类型, 使用拓扑中的名称
couple-lambda0           = vdw       ;当lambda为0(状态A)时, VDW完全打开                                 
                                     ; 作用类型, None:无;    vdw-q:所有;   vdw:仅静电 :A状态有。
                                    ;如果要使用vdw-q，话那么我们必须给甲烷分子指定电荷，可能导致不稳定
                                    ;表示该过程为去耦合，从有到无一系列的变化
couple-lambda1           = none     ;当lambda为1(状态B)时, 作用类型, None:无;  vdw-q:所有;  vdw:仅vdw；
couple-intramol          = no       ; 不对分子内相互作用进行去耦合. 也就是说, λ 因子只用于溶质溶剂之间的非键相互作用, 而不用于溶质溶质之间的非键相互作用.
nstdhdl                  = 100        ;H/λ 和 ΔH 输出到dhdl.xvg文件的频率.
separate-dhdl-file       =yes         ;输出单独的dhdl.xvg文件
;===============================================================================

3.模拟所需要的基本配置文件已经全部备好，无需再让你新建立盒子溶剂化，这两步直接省略，文件目录同教程3.2基本差不多如下：

**configura 文件下的目录结构**
├── collect_dhdl.sh             :批量收集分析所需要数据的脚本
├── batche.sh                   :批量执行job_0.sh -->job_20.sh 的脚本
├── write_mdp.sh                :批量生成mdp文件的脚本，主要修改mdp 中的init_lambda_state =nlambda 的值
├── write_sh.sh                 :批量生成job文件的脚本,主要修改job文件中 LAMBDA=Wnum的值，
├── job.sh                  :为每一窗口独立运行整个模拟过程（EM->NVT->NPT->Production_MD），即Lambda_0，
├── MDP                         :总运行参数mdp文件夹
│   ├── EM                      :能量最小化参数mdp文件夹
│   │   ├── em_l-bfgs.mdp            :第1次能量最小化参数mdp文件
│   │   ├── em_steep.mdp             :第2次能量最小化参数mdp文件
│   │   └── write_mdp.sh        : 用法：./write_mdp.sh  em_l-bfgs      
│   ├── NVT                     :等温等容预平衡参数mdp文件夹
│   │   ├── nvt.mdp             :等温等容预平衡参数mdp文件
│   │   ├── write_mdp.sh        : 用法：./write_mdp.sh  nvt     即可后接mdp文件前缀
│   ├── NPT                     :等温等压预平衡参数mdp文件夹
│   │   ├── npt.mdp             :等温等压预平衡参数mdp文件
│   │   └── write_mdp.sh        : 用法：./write_mdp.sh  npt     即可后接mdp文件前缀
│   └── Production_MD           :成品模拟参数mdp文件夹
│       ├── md.mdp             :成品模拟参数mdp文件
│       └── write_mdp.sh        : 用法：./write_mdp.sh  md     即可后接mdp文件前缀
├── Methane                     :结构文件和拓扑文件夹
│   ├── methane.gro              :含1个甲烷水盒子结构文件
│   └── topol.top               :体系top文件
└── REDERME.md

4.为每一个独立 $\lambda$ 状态生成模拟所学基本配置文件，操作过程和上诉3.2 US教程类似，这里不在赘述，只是使用脚本替换的关键词不同而已，如下：

#!/bin/bash

#对于模拟, 我们将使用shell脚本替换.mdp文件中的nlambda关键字

# 打开一个通用的.mdp文件，并替换nlambda的值

#合计21个状态值
for ((i=0;i<21;i++))
do
sed 's/nlambda/'$i'/g' $1.mdp  >$1_$i.mdp

done

模拟

在每个 $\lambda$ 状态下, 我们将进行两次能量最小化(bfgs/steep), NVT预平衡100 ps, NPT预平衡100ps, 然后进行1ns的成品模拟.

需要生成21个模拟工作流自动化执行脚本文件（job_0.sh ,job_20.sh）,然后进行批量模拟，过程同上述教程3.2 US模拟操作过程一样，这里不再赘述了。

分析

1.正常模拟结束将会产生21个Lambda_0 到Lambda_20文件夹，该文件夹内容如下，以Lambda_0为例：

├── Lambda_0                         
│   ├── EM_1                      
│   │   ├── min0.gro                    
│   │   └── ....
│   ├── EM_2
│   │   ├── min0.gro                    
│   │   └── ....
│   ├── NVT                           
│   │   ├──nvt0.gro
│   │   └── .....
│   ├── NPT                     
│   │   ├── npt0.gro             
│   │   └── .....   
│   └── PRD                    
│       ├── md0.gro
│       ├── md0.tpr                      
│       ├── dhdl.xvg   ;分析所需文件,在成品模拟时，
│       └── ....

2.关于生成分析所需要的数据文件（如：dhdl.xvg文件），需要在参数文件成品模拟mdp,和运行模拟时设置如下（以本例为例）：

#1.独立生dhdl文件，需要注意以下两步：（本教程的做法）
 (1)在md.mdp中设置以下两项:
     nstdhdl                  = 100        ; ;∂H/∂λ 和 ΔH 输出到dhdl.xvg文件的频率
     separate-dhdl-file       =yes         ;输出单独的dhdl.xvg文件
 (2)在运行成品模拟是设置 -dhdl选项,如下：(在脚本job_0中)
   gmx mdrun -nt 2 -v -deffnm md0    -dhdl dhdl
 
#2.默认输出，从md0.edr文件中获取dhdl.xvg文件：                    (替代做法)
 (1)在md.mdp中设置以下两项:
     nstdhdl                  = 100        ;∂H/∂λ 和 ΔH 输出到dhdl.xvg文件的频率
     separate-dhdl-file       =no          ;自由能的值输出到能量输出文件（ener.edr，以累积块的形式，每                                               nstenergy步一次）
 (2)在运行成品模拟是设置如下：
   gmx mdrun -nt 2 -v -deffnm md0
   
 (3)gmx energy 从md0.edr文件中获取dhdl.xvg
    gmx energy -f md0.edr -s md0.tpr -odh -dhdl.xvg
    
#3.gromacs官网的例子：<自由能的计算：水中甲烷> 设置好如下                    (教程1和2做法)
  (1)在md.mdp中设置仅一项: 
     nstdhdl                  = 100        ;∂H/∂λ 和 ΔH 输出到dhdl.xvg文件的频率
  (2)在运行成品模拟是设置如下：
   gmx mdrun -nt 2 -v -deffnm md0
 #（没设置 separate-dhdl-file=no ∂H/∂λ 和 ΔH 值不会输出到.edr文件中），仅生成md0.xvg文件

3.官网的教程教程1和翻译的教程2是默认每一个$ \lambda $不独立生成 d h d l . x v g 文件（含$ \langle \frac{ \partial H} { \partial \lambda} \rangle $和$ \Delta H $值）, 而是生成了一个 m d 0 . x v g 该文件其实是包括 d h d l . x v g 文件的数据, 可以使用 g m x b a r ，快捷的分析$ \Delta G_{AB}$

4.为了更加直观展示基于FEP计算自由能的不同分析方法，我尝试2.中的三种做法，模拟过程都一样，只不过改了些相关参数，生成了不同的数据文件，这里不再赘述。这里只重点讲分析

分析工具	分析输入数据文件
	dhdl*.xvg （2中1，2）	md*.xvg（2中3）
gmx bar	1	2
alchemical_analysis	3	4

本例子使用的参数文件是采用2中1的方式生成的 21个 $\lambda$ 状态的dhdl.xvg系列文件（dhdl.xvg）作为分析输入文件， $\langle \frac{ \partial H} { \partial \lambda} \rangle$ （用来基于TI来进行分析）和 $\Delta H$ （用来基于FEP来进行分析）值。两者H代表哈密顿值，对于孤立体系来说哈密顿量等于能量，及又可以表示为 $\langle \frac{ \partial U} { \partial \lambda} \rangle$ 和 $\Delta U$ ，2中的其他两种做法,这里仅分析，如使用md.xvg系列文件（md.xvg）。

如上表所示根据分析工具不同和分析输入文件不同，可以组合成四种不同的分析模式，实则两两相同，下面一一道来。

使用gmx bar 工具分析：

1.使用gmx bar 工具分析dhdl.xvg系列数据数据：（本教程分析方法）

#使用gmx bar 读入单独生成的dhdl.xvg系列文件或者是从md.edr系列文件提取出的dhdl.xvg：dhdl0.zvg---dhdl21.xvg
gmx bar -f dhdl*.xvg -o -oi -oh

屏幕打印出下列信息：

emperature: 300 K

Detailed results in kT (see help for explanation):
#A点的λ值   B点的λ值  自由能估计  B在A中的相对熵估计   A在B中的相对熵估计   每个样本标准偏差的估计期望
 lam_A  lam_B      DG   +/-     s_A   +/-     s_B   +/-   stdev   +/- 
     0      1    0.07  0.00    0.03  0.00    0.04  0.00    0.25  0.00
     1      2    0.06  0.00    0.03  0.00    0.03  0.00    0.26  0.00
     2      3    0.05  0.00    0.03  0.00    0.04  0.00    0.27  0.00
     3      4    0.03  0.00    0.03  0.00    0.04  0.00    0.27  0.00
     4      5    0.02  0.00    0.04  0.00    0.05  0.00    0.29  0.00
     5      6   -0.00  0.01    0.04  0.00    0.05  0.00    0.30  0.01
     6      7   -0.03  0.00    0.06  0.01    0.07  0.01    0.33  0.00
     7      8   -0.07  0.00    0.05  0.01    0.07  0.01    0.36  0.00
     8      9   -0.10  0.00    0.06  0.00    0.08  0.00    0.37  0.00
     9     10   -0.16  0.01    0.09  0.01    0.12  0.01    0.42  0.00
    10     11   -0.24  0.01    0.09  0.01    0.12  0.01    0.46  0.01
    11     12   -0.32  0.01    0.11  0.01    0.15  0.01    0.51  0.01
    12     13   -0.43  0.01    0.15  0.01    0.18  0.01    0.57  0.01
    13     14   -0.56  0.01    0.16  0.01    0.17  0.01    0.56  0.01
    14     15   -0.58  0.01    0.09  0.01    0.09  0.01    0.46  0.00
    15     16   -0.51  0.01    0.07  0.01    0.07  0.01    0.35  0.00
    16     17   -0.40  0.00    0.03  0.00    0.03  0.00    0.26  0.00
    17     18   -0.28  0.00    0.02  0.00    0.02  0.00    0.19  0.00
    18     19   -0.16  0.00    0.01  0.00    0.01  0.00    0.13  0.00
    19     20   -0.05  0.00    0.00  0.00    0.00  0.00    0.10  0.00

#注意 1Kcal/mol=4.184KJ/mol; KT(T=300K)=0.6kcal/mol
Final results in kJ/mol:
point      0 -      1,   DG  0.17 +/-  0.01
point      1 -      2,   DG  0.14 +/-  0.01
point      2 -      3,   DG  0.12 +/-  0.01
point      3 -      4,   DG  0.09 +/-  0.01
point      4 -      5,   DG  0.05 +/-  0.01
point      5 -      6,   DG -0.00 +/-  0.01
point      6 -      7,   DG -0.08 +/-  0.01
point      7 -      8,   DG -0.16 +/-  0.01
point      8 -      9,   DG -0.24 +/-  0.01
point      9 -     10,   DG -0.40 +/-  0.02
point     10 -     11,   DG -0.59 +/-  0.02
point     11 -     12,   DG -0.79 +/-  0.02
point     12 -     13,   DG -1.08 +/-  0.03
point     13 -     14,   DG -1.39 +/-  0.03
point     14 -     15,   DG -1.45 +/-  0.03
point     15 -     16,   DG -1.28 +/-  0.01
point     16 -     17,   DG -1.01 +/-  0.01
point     17 -     18,   DG -0.70 +/-  0.01
point     18 -     19,   DG -0.39 +/-  0.01
point     19 -     20,   DG -0.12 +/-  0.00


total      0 -     20,   DG -9.11 +/-  0.06

2.使用gmx bar 工具分析md.xvg系列数据数据：(教程3分析方法)

#使用gmx bar 读入生成的md0.xvg系列文件md0.xvg---md21.xvg
gmx bar -f md*.xvg -o -oi -oh

屏幕打印出下列信息：

Temperature: 300 K

Detailed results in kT (see help for explanation):

 lam_A  lam_B      DG   +/-     s_A   +/-     s_B   +/-   stdev   +/- 
     0      1    0.07  0.00    0.03  0.00    0.03  0.00    0.25  0.00
     1      2    0.06  0.00    0.03  0.00    0.04  0.00    0.26  0.00
     2      3    0.05  0.00    0.03  0.00    0.04  0.00    0.27  0.00
     3      4    0.03  0.00    0.03  0.00    0.04  0.00    0.28  0.00
     4      5    0.01  0.00    0.04  0.00    0.05  0.00    0.30  0.00
     5      6   -0.01  0.00    0.04  0.00    0.05  0.00    0.31  0.00
     6      7   -0.03  0.00    0.05  0.00    0.06  0.00    0.32  0.00
     7      8   -0.06  0.00    0.06  0.00    0.07  0.00    0.35  0.00
     8      9   -0.10  0.00    0.06  0.00    0.08  0.00    0.38  0.01
     9     10   -0.15  0.00    0.07  0.00    0.10  0.00    0.42  0.00
    10     11   -0.23  0.01    0.10  0.00    0.13  0.01    0.46  0.01
    11     12   -0.33  0.01    0.12  0.01    0.16  0.01    0.52  0.01
    12     13   -0.46  0.01    0.16  0.01    0.19  0.01    0.58  0.00
    13     14   -0.57  0.01    0.14  0.01    0.16  0.01    0.56  0.00
    14     15   -0.59  0.01    0.10  0.01    0.11  0.01    0.46  0.00
    15     16   -0.53  0.00    0.06  0.01    0.06  0.01    0.35  0.00
    16     17   -0.40  0.00    0.03  0.01    0.02  0.01    0.26  0.00
    17     18   -0.27  0.00    0.02  0.00    0.02  0.00    0.19  0.00
    18     19   -0.15  0.00    0.01  0.00    0.01  0.00    0.14  0.00
    19     20   -0.05  0.00    0.01  0.00    0.00  0.00    0.10  0.00


Final results in kJ/mol:

point      0 -      1,   DG  0.17 +/-  0.01
point      1 -      2,   DG  0.15 +/-  0.01
point      2 -      3,   DG  0.11 +/-  0.01
point      3 -      4,   DG  0.08 +/-  0.01
point      4 -      5,   DG  0.03 +/-  0.00
point      5 -      6,   DG -0.01 +/-  0.01
point      6 -      7,   DG -0.07 +/-  0.01
point      7 -      8,   DG -0.16 +/-  0.01
point      8 -      9,   DG -0.26 +/-  0.01
point      9 -     10,   DG -0.38 +/-  0.01
point     10 -     11,   DG -0.56 +/-  0.01
point     11 -     12,   DG -0.81 +/-  0.02
point     12 -     13,   DG -1.15 +/-  0.02
point     13 -     14,   DG -1.43 +/-  0.03
point     14 -     15,   DG -1.48 +/-  0.02
point     15 -     16,   DG -1.31 +/-  0.01
point     16 -     17,   DG -1.01 +/-  0.01
point     17 -     18,   DG -0.68 +/-  0.01
point     18 -     19,   DG -0.38 +/-  0.01
point     19 -     20,   DG -0.12 +/-  0.00

total      0 -     20,   DG -9.26 +/-  0.11

由上可知道本教程 $\Delta G_{AB}=-9.11±0.06kJ/mol=-2.18±0.01kcal/mol$ 与教程1中的支撑材料的值 $2.24 \pm 0.01 k c a l / m o l$ (这里是自由能是正的，是因为原论文是假设不带电的甲烷进入水中与水耦合，与本例甲烷与水解耦相反) 能很好的符合，我们使用的 $\lambda$ 向量的数目大约只有他们的一半。（一般模拟都会进行三次副本模拟，本教程为了演示，只重复一次，和教程1和2的结果有点小误差，是正常范围内的）

以上5和6利用不同的输入数据（dhdl.xvg和md.xvg）文件均会生成以下文件：

                    
├── bar.xvg          ;-o选项输出文件
├── barint.xvg       ;-oi选项输出文件                
├── histogram.xvg    ;-oh选项输出文件   
└── ...              ;更多指定生成文件见gromacs 分析程序说明手册

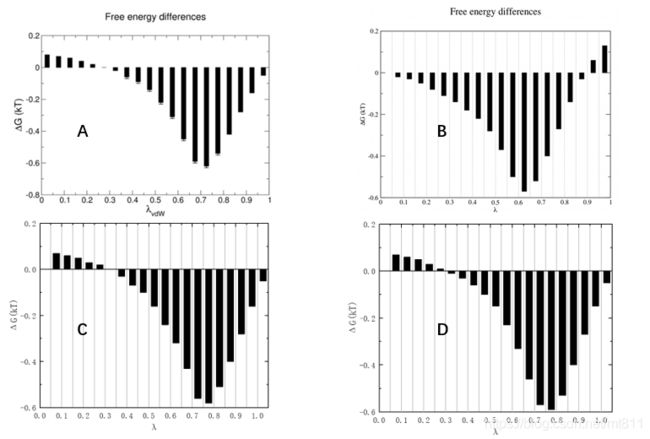
3.输出文件1: bar.xvg

从bar.xvg开始. 这个输出文件给出了每个 $\lambda$ 区间(即相邻哈密顿量之间)的相对自由能差, 并且看起来应该类似下面的图(使用柱状图绘制, 而没有使用默认的线状图, 为便于查看添加了一些网格线,可以把xvg数据复制到origin自己经过数据处理的到下图：)

图A: 为教程1中的bar.xvg分析结果图。

图B: 为教程2中的bar.xvg分析结果图，可以看出来它与ACD三个图是相反的，前面说到因为该教程是研究甲烷的溶剂化（甲烷水与发生耦合），而我们设置自由能计算时是用的去耦合（默认输出的图像自由能趋势为图ACD），为了契合主题使用对数据取反（ $\lambda=1到\lambda=0$ ）,可以看出整体数据大小和趋势四张图都是一样。

图C: 为本次教程的配置文件所生成的,使用的calc_lambda_neighbors=-1,与教程1和2的结果基本一致，重复无误。

图D: 为完全重复教程1配置文件，使用的calc_lambda_neighbors=1，与教程1分析结果图A一致，重复无误。

灰色竖线代表去耦合过程中使用的 $\lambda$ 值, 因此, 每一黑色柱代表了相邻 $\lambda$ 值之间的自由能差. 在bar.xvg文件中, 我们首先可以看到模拟中使用了什么calc_lambda_neighbors. 例如在init_lambda_state = 0的模拟中, $\lambda=0.05$ 的自由能(最近的临近窗口, 由calc_lambda_neighbors = -1设定)每nstdhdl(100)步计算一次. 这些“外部” $\lambda$ 计算可导致不同 $\lambda$ 值之间的能量发生重叠, 这样就存在相空间之间的重叠, 从而抽样充分. 感兴趣的读者可参看gmx bar说明中引用的Wu和Kofke的论文, 以了解这些概念以及熵值sA和是sB的解释.

关于输出文件barint.xvg和histogram.xvg，与分析bar.xvg类似这里就不在赘述了，详情见教程3

使用alchemical_analysis分析：

1.脚本工具安装：（python2.7+(运行环境)+pymbar(运行依赖包)+其他python依赖包+alchemical_analysis（自由能计算程序））

# 以我的centos为例：
#.1.安装python2.7+
$ sudo yum install python

#2.安装pip
$ sudo wget https://bootstrap.pypa.io/pip/2.7/get-pip.py
$ sudo python2 get-pip.py

#3.安装python依赖包
$ sudo pip2 install numpy
$ sudo pip  install six
$ sudo yum install python-devel
$ sudo pip2 install scipy
$ sudo pip install -I pyparsing==2.2.0
$ sudo pip2 install matplotlib

#4安装mbar运行分析依赖包：
$ sudo pip2 install pymbar 

#5.到alchemical_analysis目录下安装alchemical_analysis工具
$ sudo python setup.py install

#6.测试是否安装成功：屏幕出选项信息则安装成功
$ alchemical_analysis.py -h

#unbutun下:
#.1.安装python2.7+
$ sudo apt-get install python2.7

#2.安装pip,同上

#3.安装python依赖包,就安装python-dev，需要先安装aptitude
$ sudo pip2 install numpy
$ sudo pip  install six
$ sudo yum install python-devel
$ sudo pip2 install scipy

$ sudo apt-get aptitude
$ sudo  aptitude install python-dev

#4安装mbar运行分析依赖包：同上

#5.到alchemical_analysis目录下安装alchemical_analysis工具:同上

#6.测试是否安装成功：屏幕出选项信息则安装成功同上

帮助命令详情如下：

-h
显示以下帮助信息和命令选项参数使用细则

-a：指定来自软件包的数据
默认值为Gromacs;  使用: -a <software>  (software:Sire,Desmond,AMBER)
例子：使用AMBERS数据进行分析：alchemical_analysis -a AMBER

-b ：指定多少分数的能量文件用于统计计算
默认值为1.0;   使用 -b <fraction>

-c: 指定输出基于曲线拟合方法的一致性检查器。
默认值。False. 如图7a;使用   -c <boolean>
    
-d：指定存储数据文件的目录。
默认值:当前目录; 使用： -d <DATAFILE_DIRECTORY>

-e：指定从后向提取能量数据。
默认值：False;   使用      -e <boolean>

-f:绘制自由能变化在两个方向上的时间函数，时间图中指定的点数。必须提供时间点的数量（一个整数）。
默认值：0 ;  使用：-f <int>

-g:绘制所有方法的每对相邻状态的自由能差评估，包括TI的dH/dlambda曲线。
默认值：False。 -g <boolean>

-i:如果发现非相关样本的数量少于这个数字，则继续进行相关样本的分析。如果给定0，则根本不执行时间序列分析。
默认值：50

-j:自定义的结果文件名前缀。
 默认值：result        -j <string>

-k:  给出一串用'-'隔开的lambda指数，它们将被从分析中删除。(另一种方法是只让感兴趣的文件存在于目录中)。
    默认值:none。  图8分析
-m: 指定列表中的方法来估算自由能量。
  默认值。[TI, TI-CUBIC, DEXP, IEXP, BAR, MBAR]。使用：
   要添加/删除上述列表中的方法，请提供一个由方法字符串组成的字符串，前面用+/-表示                        
   例如:
    -m '-ti_cubic+gdel'将把方法变成 [TI, DEXP, IEXP, BAR, MBAR, GDEL]
    -m 'ti_cubic+gdel'将调用 [TI-CUBIC, GDEL]。
    -m 'all'将调用所有支持的方法[TI, TI-CUBIC, DEXP, IEXP, GINS, GDEL, BAR, UBAR, RBAR, MBAR]。
        
-n :用于自相关分析的观测值；可以是 "dhdl_all"（作为所有能量成分的总和）。
    默认值："dhdl"（作为那些正在变化的能量成分的总和）。或 "dE"。
    在后一种情况下，使用能量差dE_{i,i+1}（最后一个lambda的dE_{i,i-1}）。
    
-o :脚本产生的输出文件将存放在这个目录中。
    默认值：与数据文件目录相同。 使用：-o <OUTPUT_DIRECTORY>
    
-p ：指定要分析数据文件集的文的前缀，
     默认值：'dhdl'
    
-q : 数据文件集的后缀，
    默认值：'xvg'
    
-r :报告自由能的小数点位数。不用担心，这只是文本输出；全精度数据将存储在'results.pickle'中。
    默认值：3 ; 使用： -r <int>
    
-s : 丢弃此指定时间之前的数据作为 "平衡 "数据。单位皮秒。
    默认值：0 ps ;   使用： -s <time>
    
-t : 温度（K），默认值：298 K

-u : 指定报告能量的单位：'kJ'、'kcal'和'kBT'。
    默认值：'kJ'; 使用  -u <UNITS>
    
-v:  冗长选项。
    默认值。False. 

-w:打印并绘制重叠矩阵。 图7b
    默认值：False。
   报错处理：#O = MBAR.computeOverlap()[2]改成
            O = MBAR.computeOverlap()['matrix']
-x:不检查WL权重是否平衡。
   不需要日志文件作为附带输入。

-y:BAR和MBAR能量估计的收敛标准。
   默认值：1e-10。 
-z: 初始的MBAR自由能量猜测；可以是 "BAR "或 "零"。
    默认值：'bar'。

使用方法，在数据集合文件中：

alchemical_analysis -p dhdl -u kcal
或者
alchemical_analysis -t 300 -s 0 -u kcal （-w -g） ：坑
注意下-w,-g可以不要，会报错

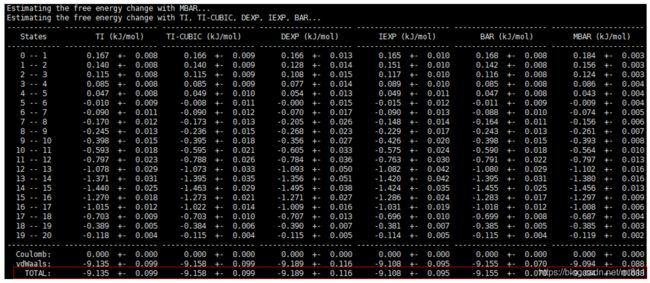
2.使用 alchemical_analysis工具分析dhdl.xvg系列数据：（本教程分析方法）

#1.calc-lambda-neighbors = -1，使用单独生成的dhdl.xvg文件的（从0-20）
#默认输出基于TI自由能计算方法（TI,TI-CUBIC）,基于FEP(DEXP.IEXP,BAR,MBAR),6种计算结果
#在含有dhdl.xvg文件夹输入下列命令
$ alchemical_analysis -p dhdl -u kJ

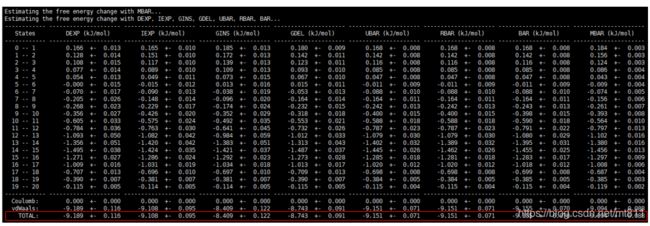
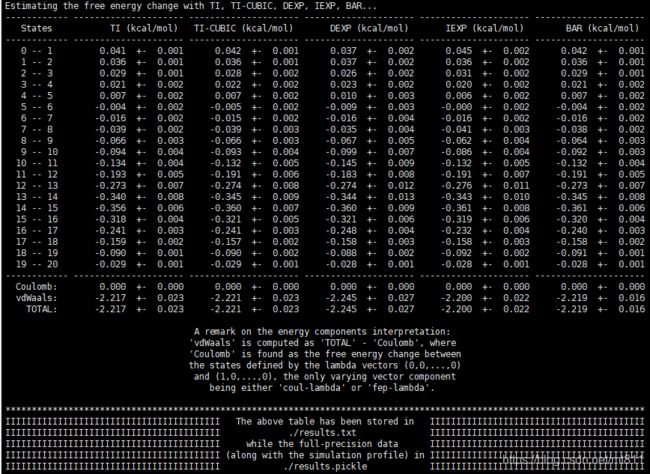
#输出全部基于FEP自由能计算方法的结果：共8种：
$ alchemical_analysis  -p dhdl -t 300 -u kJ -m 'dexp+iexp+gins+gdel+ubar+rbar+bar+mbar'

从以上两张图可以发现使用alchemical_analysis计算的自由能的结果同gmx bar分析出自由能结果是一致的均为程 $\Delta G_{AB}=-9.11±0.06kJ/mol$

（1）绘制$\Delta G $与$ \lambda$ 关系图（FEP:同bar.xvg图）

#使用 -g 选项绘制-m 选项的指定的方法的图像,fep_out是我自己指定的文件夹用来保存输出的文件
$  alchemical_analysis  -p dhdl -t 300 -u kBT -m 'dexp+iexp+gins+gdel+ubar+rbar+bar+mbar' -g -o fep_out
#会生成dF_state.pdf;dF_state_long.pdf;文件，文件图像在PDF文件中。

可以看出来与gmx bar 分析出来的bar.xvg作出来的图基本是一致的。

（2）绘制正向和反向的自由能随着模拟时间变化的函数图：本例是（forward,去耦合，那么反向就是去耦合）

#使用 -f选项，会生成dF_t.pdf文件
$ alchemical_analysis -p dhdl -u kBT -f 21 -o fep_out

（3）绘制相空间重叠矩阵

#使用 -c选项，会生成O_MBAR.pdf文件
$ alchemical_analysis -p dhdl -u kBT -c -o fep_out

(4)绘制重叠分布法：

#使用 -c选项，会生成cfm.pdf文件
$ alchemical_analysis -p dhdl -u kBT -w -o fep_out

3.使用 alchemical_analysis工具分析md.xvg系列数据：（教程2模拟生成结果，用此工具来分析）

#calc-lambda-neighbors = 1，使用md.xvg(0-20)，md.xvg里面包括dhdl.xvg的数据会发现没有了mbar选项
#与mbar相关图就没法做了如O_MBAR.pdf
$ alchemical_analysis -p md -u kcal

总结

alchemical_analysis是一款强大的自由能计算后处理分析程序，支持amber,gromacs,sire分子模拟软件包自由能计算的结果的分析，集成了matplotlib，能绘制丰富的与自由能相关图像。本程序是根据自由能专题2：计算与分析指南中自由能分析最佳做法来进行自动化处理分析的，主要有是基于TI和FEP两大自由能计算方法进行分析，并提供了大量对自由能计算结果的收敛性分析，以用来评估自由能计算结果的质量，通过与原生分析程序gmx bar（gromacs自带的）对比，可以发现，该程序不仅计算结果准确，而且还能基于同一输入文件，进行一站式的使用多种基于TI和FEP后处理方法进行自动化分析，和原生工具无需进行分析前后的数据处理与图形绘制。

3.4 TI:计算甲烷在水中的溶剂化自由能

这一部分与在gromacs中与3.3中FEP自由能计算共用一套代码，FEP生成的结果同样可以适用于基于TI自由能计算方法的后处理分析，因为前面说到，使用gromcas自由能计算代码可生成dhdl.xvg文件（含 $\langle \frac{ \partial H} { \partial \lambda} \rangle$ 和 $\Delta H$ 值）或包含dhdl.xvg文件数据的md.xvg文件，其中 $\Delta H$ 值用于基于FEP的自由能分析，而 $\langle \frac{ \partial H} { \partial \lambda} \rangle$ 用于基于TI的自由能分析。

分析

其他的均与3.3中的分析相同，就以下为TI分析图像

（1）绘制 $\langle \frac{ \partial H} { \partial \lambda} \rangle$ 与 $\lambda$ 关系图像（TI）,如图所示我们在模拟是仅开关了VDW相互作用，所下图仅显示vdw

$  alchemical_analysis  -p dhdl -t 300 -u kBT -m 'ti' -g -o fep_out
#会生成文件，文件图像在PDF文件中。

3.5.(Jarzynski Equality)非平衡近似

1.以上我们已经使用TI和FEP两种方法计算自由能，它们两者都是对称的，当 $\lambda$ 间隔足够的小，相应的 $\lambda$ 系综间有重叠时，这些方法能够给出精确的自由能估计值，而, 由于采样时间的限制, 实际情况很少这样. 与平衡方法相反, Jarzynski方法用于远离平衡的体系. 尽管考虑到我们的限制, 这听起来不错, 但由于平均问题, 需要非常多的模拟才能得到精确的自由能估计值. 最后的结果就是你并不能节省多少模拟时间. 这样, 具体使用哪种方法依赖于你要研究的问题, 要由你来决定使用哪种方法。

设置

同以FEP和TI自由能计算代码一样，主要修改自由能代码的以下部分：

delta_lambda             = 0.0001         ; 每步的增量, 慢增长方法取非零值

其他部分都是一样的

分析

1.执行完所有模拟后, 可以使用anlyze程序计算所有模拟的非可逆功：

#分析一系列的dhdl.xvg文件
$ gmx analyze -f dhdl*.xvg -integrate

注意, x值是以ps为单位的时间, 从0到20. 因此你需要将所得的功除以20使得 λλ 处于0到1之间, 间隔正确. 得到这些功后, 你可以使用你熟悉的数据分析程序创建一个直方图, 并试着将其拟合为高斯函数, 使用Jarzynski 方程(指数平均)来计算可逆功：
$exp[-\beta \Delta F]=\frac{1}{n_{sim}}\sum_{n_{sim}}exp [-\beta\int_{t_i}^{t_f}\frac{\partial V}{\partial \lambda}\frac{d V}{dt}dt]$
2.也能使用TI和FEP中的分析方法

3.6 ＭＭ/PBSA

1.使用gmx_mm/pbsa脚本计算， MM-PBSA(Molecular Mechanics-Poisson Bolzmann Surface Area, 分子力学泊松玻尔兹曼表面积)是一种对MD轨迹进行后处理以估计结合自由能的方法, 计算时会将溶剂视为均匀的连续介质, 并基于力场和隐式的连续介质模型, 对平衡轨迹中的许多帧进行平均, 以考虑温度的影响,以下教程已经很详细了，这里不在赘述：

1.MM/PBSA计算原理文章1

2.GROMACS教程：使用GROMACS计算MM-PBSA结合自由能

2.gmx_mmpbsa使用说明

3.gmx_mmpbsa脚本更新：屏蔽效应与熵贡献

安装与使用

主要工具：gromacs + gmx_mm/pbsa(脚本) + APBS，gromacs在这里的安装就不在赘述了

1.APBS 在unbutun下能直接安装：

 $ sudo  apt install apbs

2.gmx_mm/pbsa脚本：来自哲科文李老师

echo -e "\
>>>>>>>>>>>>>>>>   gmx_mmpbsa   <<<<<<<<<<<<<<<<
>>>>>>>>>>>>>>>>    Jicun Li    <<<<<<<<<<<<<<<<
>>>>>>>>>>     2020-11-15 10:11:59     <<<<<<<<<\n
>>   Usage: gmx_mmpbsa -f   *.xtc     -s   *.tpr      -n   *.ndx
                       -com COMPLEX   -pro PROTEIN   {-lig }\n
>> Default: gmx_mmpbsa -f  traj.xtc   -s topol.tpr    -n index.ndx
                       -com Complex   -pro Protein    -lig Ligand
>> Option:
     f: trajectory file
     s: topology file
     n: index file
   com: index group name of complex
   pro: index group name of protein
   lig: index group name of ligand, can be ignored using none
   change other settings in the script directly
>> Log:
   TODO:       Opt before MM-PBSA
   TODO:       CAS
   TODO:       parallel APBS, focus
   2020-11-15: fix bug for resID >=1000, for awk 3.x gsub /\s/
   2020-06-02: fix bug of withLig
   2020-06-01: fix bug of -skip
   2020-05-27: fix bug for sdie
   2020-05-26: fix bug for RES name
   2020-04-03: use C6, C12 directly
   2020-01-08: support protein only
   2019-12-24: fix bug for small time step
   2019-12-10: fix bug for OPLS force field
   2019-11-17: fix bug for c6, c12 of old version tpr
   2019-11-06: apbs FILE.apbs &> FILE.out
               on ubuntu 18.04 may not work, then delete &
   2019-11-03: fix bug for time stamp
   2019-09-19: push to gmxtool
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>\n"

################################################################################
# 设置运行环境, 计算参数
# setting up environmets and parameters
################################################################################

trj=traj.xtc		# 轨迹文件 trajectory file
tpr=topol.tpr		# tpr文件  tpr file
ndx=index.ndx		# 索引文件 index file

com=Complex			# 复合物索引组 index group name of complex
pro=Protein			# 蛋白索引组   index group name of protein
lig=Ligand			# 配体索引组   index group name of ligand

step=1	# 从第几步开始运行 step number to run
		# 1. 预处理轨迹: 复合物完整化, 团簇化, 居中叠合, 然后生成pdb文件
		#    pre-processe trajectory, whole, cluster, center, fit, then generate pdb file
		# 2. 获取每个原子的电荷, 半径, LJ参数, 然后生成qrv文件
		#    abstract atomic parameters, charge, radius, C6/C12, then generate qrv file
		# 3. MM-PBSA计算: pdb->pqr, 输出apbs, 计算MM, APBS
		#    run MM-PBSA, pdb->pqr, apbs, then calculate MM, PB, SA

gmx='gmx'								# /path/to/GMX/bin/gmx_mpi
dump="$gmx dump"						# gmx dump
trjconv="$gmx trjconv -dt 1000"			# gmx trjconv, use -b -e -dt, NOT -skip

#apbs='/path/APBS/bin/apbs'				# APBS(Linux)
apbs='c:/apbs1.5/bin/apbs.exe'			# APBS(Windows), USE "/", NOT "\"
export MCSH_HOME=/dev/null				# APBS io.mc

pid=pid				# 输出文件($$可免重复) prefix of the output files($$)
scr=_$pid.scr		# 屏幕输出文件 file to save the message from the screen
qrv=_$pid.qrv		# 电荷/半径/VDW参数文件 to save charge/radius/vdw parmeters

radType=1			# 原子半径类型 radius of atoms (0:ff; 1:mBondi; 2:Bondi)
radLJ0=1.2			# 用于LJ参数原子的默认半径(A, 主要为H) radius when LJ=0 (H)

meshType=0			# 网格大小 mesh (0:global  1:local)
gridType=1			# 格点大小 grid (0:GMXPBSA 1:psize)

cfac=3				# 分子尺寸到粗略格点的放大系数
					# Factor to expand mol-dim to get coarse grid dim
fadd=10				# 分子尺寸到细密格点的增加值(A)
					# Amount added to mol-dim to get fine grid dim (A)
df=.5				# 细密格点间距(A) The desired fine mesh spacing (A)

# 极性计算设置(Polar)
PBEset='
  temp  298.15      # 温度
  pdie  2           # 溶质介电常数
  sdie  78.54       # 溶剂介电常数, 真空1, 水78.54

  lpbe              # PB方程求解方法, lpbe(线性), npbe(非线性), smbpe(大小修正)
  bcfl  mdh         # 粗略格点PB方程的边界条件, zero, sdh/mdh(single/multiple Debye-Huckel), focus, map
  srfm  smol        # 构建介质和离子边界的模型, mol(分子表面), smol(平滑分子表面), spl2/4(三次样条/7阶多项式)
  chgm  spl4        # 电荷映射到格点的方法, spl0/2/4, 三线性插值, 立方/四次B样条离散
  swin  0.3         # 立方样条的窗口值, 仅用于 srfm=spl2/4

  srad  1.4         # 溶剂探测半径
  sdens 10          # 表面密度, 每A^2的格点数, (srad=0)或(srfm=spl2/4)时不使用

  ion  1 0.15 0.95  # 阳离子的电荷, 浓度, 半径
  ion -1 0.15 1.81  # 阴离子

  calcforce  no
  calcenergy comps'

# 非极性计算设置(Apolar/Non-polar)
PBAset='
  temp  298.15 # 温度
  srfm  sacc   # 构建溶剂相关表面或体积的模型
  swin  0.3    # 立方样条窗口(A), 用于定义样条表面

  # SASA
  srad  1.4    # 探测半径(A)
  gamma 1      # 表面张力(kJ/mol-A^2)

  #gamma const 0.027     0        # 表面张力, 常数
  #gamma const 0.0226778 3.84928  # 表面张力, 常数

  press  0     # 压力(kJ/mol-A^3)
  bconc  0     # 溶剂本体密度(A^3)
  sdens 10
  dpos  0.2
  grid  0.1 0.1 0.1

  # SAV
  #srad  1.29      # SAV探测半径(A)
  #press 0.234304  # 压力(kJ/mol-A^3)

  # WCA
  #srad   1.25           # 探测半径(A)
  #sdens  200            # 表面的格点密度(1/A)
  #dpos   0.05           # 表面积导数的计算步长
  #bconc  0.033428       # 溶剂本体密度(A^3)
  #grid   0.45 0.45 0.45 # 算体积分时的格点间距(A)

  calcforce no
  calcenergy total'

################################################################################
# 检查 gmx, apbs 是否可以运行
# check gmx, apbs
################################################################################

str=$($gmx --version | grep -i "GROMACS version")
[[ -z "$str" ]] && { echo -e "!!! WARNING !!! GROMACS NOT available !\n"; }

str=$($apbs --version | grep -i "Poisson-Boltzmann")
[[ -z "$str" ]] && { echo -e "!!! WARNING !!!  APBS   NOT available !\n"; }

################################################################################
# 解析命令行参数
# parse command line options
################################################################################

opt=($*); N=${#opt[@]}
for((i=0; i<N; i++)); do
	arg=${opt[$i]}; j=$((i+1)); val=${opt[$j]}
	[[ $arg =~ -f   ]] && { trj=$val; }
	[[ $arg =~ -s   ]] && { tpr=$val; }
	[[ $arg =~ -n   ]] && { ndx=$val; }
	[[ $arg =~ -com ]] && { com=$val; }
	[[ $arg =~ -pro ]] && { pro=$val; }
	[[ $arg =~ -lig ]] && { lig=$val; }
done

withLig=1; [[ $lig =~ none ]] && { withLig=0; com=$pro; lig=$pro; }

################################################################################
# 检查文件
# check files
################################################################################

[[ ! -f "$trj" ]] && { echo -e "!!! ERROR !!! trajectory File NOT Exist !\n"; exit; }
[[ ! -f "$tpr" ]] && { echo -e "!!! ERROR !!! topology   File NOT Exist !\n"; exit; }
[[ ! -f "$ndx" ]] && { echo -e "!!! ERROR !!! index      File NOT Exist !\n"; exit; }
str=$(grep $com "$ndx"); [[ -z "$str" ]] && { echo -e "!!! ERROR !!! $com NOT in $ndx !\n"; exit; }
str=$(grep $pro "$ndx"); [[ -z "$str" ]] && { echo -e "!!! ERROR !!! $pro NOT in $ndx !\n"; exit; }
str=$(grep $lig "$ndx"); [[ -z "$str" && $withLig -eq 1 ]] && { echo -e "!!! ERROR !!! $lig NOT in $ndx !\n"; exit; }

if [[ $step -le 1 ]]; then
################################################################################
# 1. 预处理轨迹: 复合物完整化, 团簇化, 居中叠合, 然后生成pdb文件
#    请检查pdb文件确保构型PBC处理正确
# 1. pre-processe trajectory, whole, cluster, center, fit, then generate pdb file
################################################################################
trjwho=$pid~who; trjcnt=$pid~cnt; trjcls=$pid~cls
echo $com            | $trjconv  -s $tpr -n $ndx -f $trj    -o $trjwho.xtc &> $scr -pbc whole
echo -e "$lig\n$com" | $trjconv  -s $tpr -n $ndx -f $trjwho -o _$pid.pdb   &>>$scr -pbc mol -center

# usful for single protein and ligand
#echo $com            | $trjconv  -s $tpr -n $ndx -f $trj    -o $trjwho.xtc &> $scr -pbc whole
#echo -e "$lig\n$com" | $trjconv  -s $tpr -n $ndx -f $trjwho -o $trjcnt.xtc &>>$scr -pbc mol -center
#echo -e "$com\n$com" | $trjconv  -s $tpr -n $ndx -f $trjcnt -o $trjcls.xtc &>>$scr -pbc cluster
#echo -e "$lig\n$com" | $trjconv  -s $tpr -n $ndx -f $trjcls -o _$pid.pdb   &>>$scr -fit rot+trans

fi; if [[ $step -le 2 ]]; then
################################################################################
# 2. 获取每个原子的电荷, 半径, LJ参数, 然后生成qrv文件
# 2. abstract atomic parameters, charge, radius, C6/C12, then generate qrv file
#    feel free to change radius with radType
#    radType=0: radius from C6/C12, or radLJ0 if either C6 or C12 is zero
#    radType=1: mBondi
#    radType=2: Bondi
################################################################################
$dump -quiet -s $tpr 2>>$scr \
| awk >$qrv -v ndx=$ndx -v pro=$pro -v lig=$lig -v withLig=$withLig \
			-v radType=$radType -v radLJ0=$radLJ0 '
	BEGIN { RS="["
		print pro, lig
		while(getline < ndx) {
			gsub(" ","", $1); gsub("\t","", $1)
			if($1==pro)    for(i=3; i<=NF; i++) ndxPro[$i+0]++
			if($1==pro"]") for(i=2; i<=NF; i++) ndxPro[$i+0]++
			if(withLig) {
				if($1==lig)    for(i=3; i<=NF; i++) ndxLig[$i+0]++
				if($1==lig"]") for(i=2; i<=NF; i++) ndxLig[$i+0]++
			}
		}
		RS="\r?\n"
		nres=0
	}

	/#molblock/  { Ntyp=$3 }
	/moltype.+=/ { Imol=$3; getline; Nmol[Imol]=$3 }
	/ffparams:/ {
		getline Atyp; sub(/.+=/, "", Atyp); Atyp += 0
		print Atyp
		getline
		for(i=0; i$0; sub(".*c6 *= *",  "", C6);  sub(",.*", "", C6);
				C12=$0; sub(".*c12 *= *", "", C12); sub(",.*", "", C12);
				printf " %s %s", C6, C12
				if(j==i) {
					sigma[i]=0; epsilon[i]=0
					Rad[i]=radLJ0
					if(C6*C12!=0) {
						sigma[i]=10*(C12/C6)^(1./6) # 转换单位为A
						epsilon[i]=C6^2/(4*C12)
						Rad[i]=.5*sigma[i]          # sigma为直径
					}
				}
			}
			print ""
		}
	}

	/moltype.+\(/ { Imol=$0; gsub(/[^0-9]/,"",Imol)
		getline txt; sub(/.*=/,"",txt); gsub(" ","_",txt)
		Name[Imol]=txt
		getline; getline txt;       gsub(/[^0-9]/,"",txt); Natm[Imol]=txt+0
		for(i=0; i$0; idx=$3; resID[Imol, i]=$(NF-2)+1+nres
			sub(",", "", idx);    idx += 0;
			Catm[Imol, i]=idx
			Ratm[Imol, i]=Rad[idx]
			Satm[Imol, i]=sigma[idx]
			Eatm[Imol, i]=epsilon[idx]
			sub(/.+q=/, "", txt); sub(/,.+/,  "", txt); Qatm[Imol, i]=txt
		}
		getline
		for(i=0; i$0); sub(/".*/,"",$0);
		resName[nres]=sprintf("%d%s", nres, $0)
	}

	END {
		Ntot=0; Nidx=0
		for(i=0; i0) radi=getRadi(Tatm[i, j], radType)
						printf "%6d %9.5f %9.6f %6d %9.6f %9.6f %6d %s %s %-6s  ",  \
						Nidx, Qatm[i,j], radi, Catm[i,j], Satm[i,j], Eatm[i,j], \
						Ntot, Name[i]"-"n+1"."j+1, \
						resName[resID[i,j]], Tatm[i, j]
						if(Ntot in ndxPro) print "Pro"
						if(Ntot in ndxLig) print "Lig"
					}
				}
			}
		}
	}

	function getRadi(tag, radType) {
		radBondi["O" ]= 1.50; if(radType==2) radBondi["O" ]= 1.52
		radBondi["S" ]= 1.80; if(radType==2) radBondi["S" ]= 1.83
		radBondi["P" ]= 1.85; if(radType==2) radBondi["P" ]= 1.80
		radBondi["I" ]= 1.98; if(radType==2) radBondi["I" ]= 2.06
		radBondi["BR"]= 1.85; if(radType==2) radBondi["BR"]= 1.92
		radBondi["N" ]= 1.55
		radBondi["F" ]= 1.47
		radBondi["CL"]= 1.77

		radBondi["C" ]= 1.70; radBondi["H" ]= 1.20
		radBondi["C*"]= 1.77; radBondi["H4"]= 1.00
		radBondi["CA"]= 1.77; radBondi["H5"]= 1.00
		radBondi["CB"]= 1.77; radBondi["HA"]= 1.00
		radBondi["CC"]= 1.77; radBondi["HC"]= 1.30
		radBondi["CD"]= 1.77; radBondi["HN"]= 1.30
		radBondi["CN"]= 1.77; radBondi["HP"]= 1.30
		radBondi["CR"]= 1.77; radBondi["HO"]= 0.80
		radBondi["CV"]= 1.77; radBondi["HS"]= 0.80
		radBondi["CW"]= 1.77;

		tag=toupper(tag)
		if(length(tag)>=2) {
			if(!radBondi[substr(tag,1,2)]) return radBondi[substr(tag,1,1)]
			else return radBondi[substr(tag,1,2)]
		}
		return radBondi[tag]
	}
'

fi; if [[ $step -le 3 ]]; then
################################################################################
# 3. MM-PBSA计算: pdb->pqr, 输出apbs, 计算MM, APBS
# 3. run MM-PBSA, pdb->pqr, apbs, then calculate MM, PB, SA
################################################################################
dt=$(awk '/t=/{n++;sub(/.*t=/,"");sub(/step=.*/,"");t[n]=$0;if(n==2){print t[n]-t[1];exit}}' _$pid.pdb)
awk -v pid=_$pid  -v qrv=$qrv -v apbs="$apbs" \
	-v ff=$ff     -v PBEset="$PBEset" -v PBAset="$PBAset" \
	-v meshType=$meshType -v gridType=$gridType -v gmem=$gmem  \
	-v fadd=$fadd -v cfac=$cfac -v df=$df -v dt="$dt"          \
	-v withLig=$withLig -v RS="\r?\n" '
	BEGIN {
		getline < qrv
		getline Atyp < qrv
		for(i=0; i$(2+2*j); C12[i,j]=$(3+2*j) }
		}
		while(getline < qrv) {
			Qatm[$1]=$2; Ratm[$1]=$3; Catm[$1]=$4
			Satm[$1]=$5; Eatm[$1]=$6
			if($NF=="Pro") { Npro++; if(Npro==1) Ipro=$1
				ndxPro[$1]++; resPro[Npro]="P~"$(NF-2)
			}
			if($NF=="Lig") { Nlig++; if(Nlig==1) Ilig=$1
				ndxLig[$1]++; resLig[Nlig]="L~"$(NF-2)
			}
		}
		close(qrv)
		Ncom=Npro+Nlig

		PBEset0=PBEset; sub(/sdie +[0-9]*\.*[0-9]*/, "sdie  1", PBEset0)

		txt=PBEset; sub(/.*pdie +/, "", txt);
		sub(/\n.*/, "", txt); split(txt, arr)
		pdie=arr[1]

		txt=PBAset; sub(/.*#gamma +con[a-zA-Z]+/, "", txt);
		sub(/\n.*/, "", txt); split(txt, arr)
		gamma=arr[1]; const=arr[2]

		MAXPOS=1E9
		minX= MAXPOS; maxX=-MAXPOS;
		minY= MAXPOS; maxY=-MAXPOS;
		minZ= MAXPOS; maxZ=-MAXPOS

		fmt=sprintf("%.9f",dt/1E3)
		sub(/0*$/,"",fmt);sub(/.*\./,"",fmt)
		fmt="~%."length(fmt)"fns"
	}

	/REMARK/ {next}
	/TITLE/ {Fout=FILENAME
		txt=$0; sub(/.*t= */,"",txt); sub(/ .*/,"",txt)
		txt=sprintf(fmt, txt/1E3);
		sub(".pdb", txt, Fout)
		Nfrm++; n=0
		Fname[Nfrm]=Fout

		minXpro[Nfrm]= MAXPOS; minXlig[Nfrm]= MAXPOS;
		minYpro[Nfrm]= MAXPOS; minYlig[Nfrm]= MAXPOS;
		minZpro[Nfrm]= MAXPOS; minZlig[Nfrm]= MAXPOS

		maxXpro[Nfrm]=-MAXPOS; maxXlig[Nfrm]=-MAXPOS
		maxYpro[Nfrm]=-MAXPOS; maxYlig[Nfrm]=-MAXPOS
		maxZpro[Nfrm]=-MAXPOS; maxZlig[Nfrm]=-MAXPOS
	}
	/^ATOM/ {
		ATOM=substr($0,1,6)
		INDX=substr($0,7,5)+0
		NAME=substr($0,13,4)
		RES =substr($0,18,3)
		CHN =substr($0,22,1); if(CHN=" ") CHN="A"
		NUM =substr($0,23,4)
		X   =substr($0,31,8); X += 0
		Y   =substr($0,39,8); Y += 0
		Z   =substr($0,47,8); Z += 0
		r=Ratm[INDX]

		txt=sprintf("%-6s%5d %-4s %3s %s%4d    %8.3f %8.3f %8.3f %12.6f %12.6f", \
			ATOM, INDX, NAME, RES, CHN, NUM, X, Y, Z, Qatm[INDX], r)

		if(INDX in ndxPro) {
			print txt > Fout"_pro.pqr"
			minXpro[Nfrm]=min(minXpro[Nfrm], X-r); maxXpro[Nfrm]=max(maxXpro[Nfrm], X+r)
			minYpro[Nfrm]=min(minYpro[Nfrm], Y-r); maxYpro[Nfrm]=max(maxYpro[Nfrm], Y+r)
			minZpro[Nfrm]=min(minZpro[Nfrm], Z-r); maxZpro[Nfrm]=max(maxZpro[Nfrm], Z+r)
		}

		if(withLig) {
			print txt > Fout"_com.pqr"
			if(INDX in ndxLig) {
				print txt > Fout"_lig.pqr"
				minXlig[Nfrm]=min(minXlig[Nfrm], X-r); maxXlig[Nfrm]=max(maxXlig[Nfrm], X+r)
				minYlig[Nfrm]=min(minYlig[Nfrm], Y-r); maxYlig[Nfrm]=max(maxYlig[Nfrm], Y+r)
				minZlig[Nfrm]=min(minZlig[Nfrm], Z-r); maxZlig[Nfrm]=max(maxZlig[Nfrm], Z+r)
			}
		}

		minXcom[Nfrm]=min(minXpro[Nfrm], minXlig[Nfrm]); maxXcom[Nfrm]=max(maxXpro[Nfrm], maxXlig[Nfrm])
		minYcom[Nfrm]=min(minYpro[Nfrm], minYlig[Nfrm]); maxYcom[Nfrm]=max(maxYpro[Nfrm], maxYlig[Nfrm])
		minZcom[Nfrm]=min(minZpro[Nfrm], minZlig[Nfrm]); maxZcom[Nfrm]=max(maxZpro[Nfrm], maxZlig[Nfrm])

		minX=min(minX, minXcom[Nfrm]); maxX=max(maxX, maxXcom[Nfrm])
		minY=min(minY, minYcom[Nfrm]); maxY=max(maxY, maxYcom[Nfrm])
		minZ=min(minZ, minZcom[Nfrm]); maxZ=max(maxZ, maxZcom[Nfrm])

		next
	}

	END{
		kJcou=1389.35457520287
		Rcut=1E10              # large enough

		for(i=1; i<=Npro; i++) dE[resPro[i]]=0
		for(i=1; i<=Nlig; i++) dE[resLig[i]]=0
		Nres=asorti(dE, Tres)

		txt="   #Frame   "
		for(i=1; i<=Nres; i++) {
			ii=Tres[i]; sub(/~0+/, "~", ii)
			txt = txt""sprintf("%12s", ii)
		}
		if(withLig) {
			print txt > pid"~resMM.dat"
			print txt > pid"~resMM_COU.dat"
			print txt > pid"~resMM_VDW.dat"
			print txt > pid"~res_MMPBSA.dat"
		}
		print txt > pid"~resPBSA.dat"
		print txt > pid"~resPBSA_PB.dat"
		print txt > pid"~resPBSA_SA.dat"

		print "   #Frame      Binding    MM        PB        SA     "\
			 "|   COU       VDW     |       PBcom        PBpro        PBlig  "\
			 "|    SAcom     SApro     SAlig" >> pid"~MMPBSA.dat"

		for(fr=1; fr<=Nfrm; fr++) {
			Fout=Fname[fr]
			print "running for Frame "fr": "Fout

			txt=Fout"_pro.pqr"; if(withLig) txt=Fout"_com.pqr";
			close(txt)
			n=0;
			while(getline < txt) { n++;
				type[n]=$3; res[n]=$4;
				x[n]=$(NF-4);    y[n]=$(NF-3);   z[n]=$(NF-2)
				resID[n]=$(NF-5); gsub(/[A-Z]+/, "", resID[n])
			}
			close(txt)

			# MM
			if(withLig) {
				for(i=1; i<=Npro; i++) { dEcou[resPro[i]]=0; dEvdw[resPro[i]]=0 }
				for(i=1; i<=Nlig; i++) { dEcou[resLig[i]]=0; dEvdw[resLig[i]]=0 }
				for(i=1; i<=Npro; i++) {
					ii=i+Ipro-1
					qi=Qatm[ii]; ci=Catm[ii]; si=Satm[ii]; ei=Eatm[ii]
					xi=x[ii]; yi=y[ii]; zi=z[ii]
					for(j=1; j<=Nlig; j++) {
						jj=j+Ilig-1; cj=Catm[jj]
						r=sqrt( (xi-x[jj])^2+(yi-y[jj])^2+(zi-z[jj])^2 )
						if(r Fout".apbs"
			else        print "read\n" \
				"  mol pqr "Fout"_pro.pqr\n" \
				"end\n\n" > Fout".apbs"

			if(meshType==0) { # GMXPBSA
				if(withLig) print \
					dimAPBS(Fout"_com", 1, minX, maxX, minY, maxY, minZ, maxZ), \
					dimAPBS(Fout"_pro", 2, minX, maxX, minY, maxY, minZ, maxZ), \
					dimAPBS(Fout"_lig", 3, minX, maxX, minY, maxY, minZ, maxZ)  > Fout".apbs"
				else        print \
					dimAPBS(Fout"_pro", 1, minX, maxX, minY, maxY, minZ, maxZ)  > Fout".apbs"
			} else if(meshType==1) { # g_mmpbsa
				if(withLig) print \
					dimAPBS(Fout"_com", 1, minXcom[fr], maxXcom[fr], minYcom[fr], maxYcom[fr], minZcom[fr], maxZcom[fr]), \
					dimAPBS(Fout"_pro", 2, minXpro[fr], maxXpro[fr], minYpro[fr], maxYpro[fr], minZpro[fr], maxZpro[fr]), \
					dimAPBS(Fout"_lig", 3, minXlig[fr], maxXlig[fr], minYlig[fr], maxYlig[fr], minZlig[fr], maxZlig[fr])  > Fout".apbs"
				else       print \
					dimAPBS(Fout"_pro", 1, minXpro[fr], maxXpro[fr], minYpro[fr], maxYpro[fr], minZpro[fr], maxZpro[fr])  > Fout".apbs"
			}

			cmd=apbs" "Fout".apbs > "Fout".out 2>&1";
			system(cmd); close(cmd)

			txt=Fout".out";
			while(getline < txt ) {
				if(index($0, "CALCULATION #")) {
					if(index($0, "("Fout"_com")) { t=1; n=Ncom }
					if(index($0, "("Fout"_pro")) { t=2; n=Npro }
					if(index($0, "("Fout"_lig")) { t=3; n=Nlig }
					if(index($0, "~VAC)")) t += 10
					if(index($0, "~SAS)")) t += 20
					while(getline < txt) {
						if(t<20 && index($0, "Per-atom energies:") \
						|| t>20 && index($0, "Solvent Accessible Surface Area")) break
					}

					for(i=1; i<=n; i++) {
						getline $3; else r=$NF
						if(t<10)       Esol[t%10, i]=r
						else if(t<20)  Evac[t%10, i]=r
						else if(t<30)  Esas[t%10, i]=gamma*r+const/n
					}
				}
			}
			close(txt)

			PBcom=0; SAcom=0;
			PBpro=0; SApro=0;
			PBlig=0; SAlig=0;
			for(i=1; i<=Ncom; i++) { Esol[1,i] -= Evac[1,i]; PBcom += Esol[1,i]; SAcom += Esas[1,i] }
			for(i=1; i<=Npro; i++) { Esol[2,i] -= Evac[2,i]; PBpro += Esol[2,i]; SApro += Esas[2,i] }
			for(i=1; i<=Nlig; i++) { Esol[3,i] -= Evac[3,i]; PBlig += Esol[3,i]; SAlig += Esas[3,i] }

			for(i=1; i<=Npro; i++) { PBres[resPro[i]]=0; SAres[resPro[i]]=0 }
			for(i=1; i<=Nlig; i++) { PBres[resLig[i]]=0; SAres[resLig[i]]=0 }
			for(i=1; i<=Npro; i++) {
				PBres[resPro[i]] += Esol[1, Ipro+i-1]-Esol[2, i]
				SAres[resPro[i]] += Esas[1, Ipro+i-1]-Esas[2, i]
			}
			for(i=1; i<=Nlig; i++) {
				PBres[resLig[i]] += Esol[1, Ilig+i-1]-Esol[3, i]
				SAres[resLig[i]] += Esas[1, Ilig+i-1]-Esas[3, i]
			}

			preK=-1; if(withLig) preK=1
			printf "%-12s %9.3f %9.3f %9.3f %9.3f | %9.3f %9.3f | %12.3f %12.3f %12.3f | %9.3f %9.3f %9.3f\n", \
				Fout,       preK*(Ecou+Evdw+PBcom-PBpro-PBlig+SAcom-SApro-SAlig), \
				Ecou+Evdw,  preK*(PBcom-PBpro-PBlig), preK*(SAcom-SApro-SAlig), \
				Ecou, Evdw, PBcom, PBpro, PBlig, SAcom, SApro, SAlig >> pid"~MMPBSA.dat"

			fmt="%s%12.3f%s"
			for(i=1; i<=Nres; i++) {
				ii="";  if(i==1) ii=sprintf("%-12s", Fout)
				txt=""; if(i==Nres) txt="\n"
				if(withLig) {
					printf fmt, ii, dEcou[Tres[i]], txt                > pid"~resMM_COU.dat"
					printf fmt, ii, dEvdw[Tres[i]], txt                > pid"~resMM_VDW.dat"
					printf fmt, ii, dEcou[Tres[i]]+dEvdw[Tres[i]], txt > pid"~resMM.dat"
					printf fmt, ii, dEcou[Tres[i]]+dEvdw[Tres[i]] \
								   +PBres[Tres[i]]+SAres[Tres[i]], txt > pid"~res_MMPBSA.dat"
				}
				printf fmt, ii, preK*(PBres[Tres[i]]), txt                > pid"~resPBSA_PB.dat"
				printf fmt, ii, preK*(SAres[Tres[i]]), txt                > pid"~resPBSA_SA.dat"
				printf fmt, ii, preK*(PBres[Tres[i]]+SAres[Tres[i]]), txt > pid"~resPBSA.dat"
			}

			fmt="%s%6.1f%6.1f\n"
			for(i=1; i<=Npro; i++) {
				ii=Ipro+i-1
				txt=sprintf("%-6s%5d %-4s %3s A%4d    %8.3f%8.3f%8.3f", \
					"ATOM", ii, type[ii], res[ii], resID[ii], x[ii], y[ii], z[ii])
				if(withLig) {
					printf fmt, txt, dEcou[resPro[i]], dEvdw[resPro[i]] > Fout"~COU+VDW.pdb"
					printf fmt, txt, dEcou[resPro[i]]+dEvdw[resPro[i]], \
								 PBres[resPro[i]]+SAres[resPro[i]]  > Fout"~res_MM+PBSA.pdb"
				}
				printf fmt, txt, preK*PBres[resPro[i]], preK*SAres[resPro[i]] > Fout"~PB+SA.pdb"
				printf fmt, txt, 0, dEcou[resPro[i]]+dEvdw[resPro[i]]  \
								+preK*(PBres[resPro[i]]+SAres[resPro[i]])  > Fout"~res_MMPBSA.pdb"
			}
			for(i=1; i<=Nlig; i++) {
				ii=Ilig+i-1
				txt=sprintf("%-6s%5d %-4s %3s A%4d    %8.3f%8.3f%8.3f", \
					 "ATOM", ii, type[ii], res[ii], resID[ii], x[ii], y[ii], z[ii])
				printf fmt, txt, dEcou[resLig[i]], dEvdw[resLig[i]] > Fout"~COU+VDW.pdb"
				printf fmt, txt, PBres[resLig[i]], SAres[resLig[i]] > Fout"~PB+SA.pdb"
				printf fmt, txt, dEcou[resLig[i]]+dEvdw[resLig[i]], \
								 PBres[resLig[i]]+SAres[resLig[i]]  > Fout"~res_MM+PBSA.pdb"
				printf fmt, txt, 0, dEcou[resLig[i]]+dEvdw[resLig[i]]  \
								+PBres[resLig[i]]+SAres[resLig[i]]  > Fout"~res_MMPBSA.pdb"
			}
		}
	}

	function dimAPBS(file, Imol, minX, maxX, minY, maxY, minZ, maxZ) {

		lenX=max(maxX-minX, 0.1); cntX=(maxX+minX)/2
		lenY=max(maxY-minY, 0.1); cntY=(maxY+minY)/2
		lenZ=max(maxZ-minZ, 0.1); cntZ=(maxZ+minZ)/2
		cX  =lenX*cfac;           fX  =min(cX, lenX+fadd)
		cY  =lenY*cfac;           fY  =min(cY, lenY+fadd)
		cZ  =lenZ*cfac;           fZ  =min(cZ, lenZ+fadd)

		levN=4    # 划分级别
		t=2^(levN+1)
		nX=round(fX/df)-1; nX=max(t*round(nX/t)+1, 33)
		nY=round(fY/df)-1; nY=max(t*round(nY/t)+1, 33)
		nZ=round(fZ/df)-1; nZ=max(t*round(nZ/t)+1, 33)

		if(gridType==0) { # GMXPBSA method
			fpre=1; cfac=1.7
			fX=lenX+2*fadd; cX=fX*cfac; nX=t*(int(fX/(t*df))+1+fpre)+1
			fY=lenY+2*fadd; cY=fY*cfac; nY=t*(int(fY/(t*df))+1+fpre)+1
			fZ=lenZ+2*fadd; cZ=fZ*cfac; nZ=t*(int(fZ/(t*df))+1+fpre)+1
		}

		MGset="mg-auto"
		mem = 200*nX*nY*nZ/1024./1024. # MB

#		npX=nX; npY=nY; npZ=nZ
#		gmem=4000
#		ofrac=0.1
#		if(mem>=gmem) {
#			while(mem>gmem) {
#				maxN=max(npX, max(npY, npZ))
#					 if(maxN==npX) npX = t*((npX-1)/t-1)+1
#				else if(maxN==npY) npY = t*((npY-1)/t-1)+1
#				else if(maxN==npZ) npZ = t*((npZ-1)/t-1)+1
#				mem = 200*npX*npY*npZ/1024./1024
#			}

#			t=nX/npX; if(t>1) npX = int(t*(1+2*ofrac) + 1.0);
#			t=nY/npY; if(t>1) npY = int(t*(1+2*ofrac) + 1.0);
#			t=nZ/npZ; if(t>1) npZ = int(t*(1+2*ofrac) + 1.0);
#			MGset="mg-para\n  ofrac "ofrac"\n  pdime "npX" "npY" "npZ
#		}

		XYZset="  "MGset \
			"\n  mol "Imol \
			"\n  dime   "nX"  "nY"  "nZ"        # 格点数目, 所需内存: "mem" MB"  \
			"\n  cglen  "cX"  "cY"  "cZ"        # 粗略格点长度" \
			"\n  fglen  "fX"  "fY"  "fZ"        # 细密格点长度" \
			"\n  fgcent "cntX"  "cntY"  "cntZ"  # 细密格点中心" \
			"\n  cgcent "cntX"  "cntY"  "cntZ"  # 粗略格点中心"

		return \
			"ELEC name "file"\n" \
			XYZset "\n" \
			PBEset "\n" \
			"end\n\n" \
			"ELEC name "file"~VAC\n" \
			XYZset  "\n" \
			PBEset0 "\n" \
			"end\n\n" \
			"APOLAR name "file"~SAS\n" \
			"  mol "Imol"\n" \
			PBAset"\n" \
			"end\n\n" \
			"print elecEnergy "file" - "file"~VAC end\n" \
			"print apolEnergy "file"~SAS end\n\n"
	}
	function min(x, y) { return xy ? x : y }
	function round(x)  { return int(x+0.5)  }
' _$pid.pdb
fi

################################################################################
# 4. 删除临时文件
# 4. remove intermediate files
################################################################################
#rm -f $trjwho.xtc $trjcnt.xtc $trjcls.xtc
#rm -f io.mc _$pid.pdb $scr $qrv \#_$pid*\#

3.7 MtD

1.Metadynamics（MtD）可以使用PLUMED 和Colvars等分子模拟计算自由能的插件，限于篇幅问题下次更新做单独的更新

3.8.进阶教程：使用gromacs计算配体与受体的结合自由能

1.设置

该过程如下图所示，在文章1中已经进行了详细的描述，可前去了解，这里只挂出示意图：

在这个热力学循环中，我们需要模拟的系统由它们周围的黑色圆圈表示，限制势的存在由回形针指示，白色配体意味着它不与环境相互作用（但仍存在分子内作用），蓝色表示显示水溶剂环境。
$A状态：L+(Water)--->L_{elec+vdw}$

A状态下：假设蛋白质（P）与小分子（L）远离，此时L与P之间还没有相互作用,L体系与环境（如溶剂水）间具有相互作用（橙色表示有相互作用：L与水耦合）主要为静电相互作用L(elec)，非静电相互作用(VDW)为溶剂化自由能（ΔG(solve)）
$B状态：L_{elec+vdw}----->L+(Water)$

B状态：分别慢慢关闭 L与环境(Water)间的相互作用，即小分子－溶剂间的 ele和 vdw，此时的小分子如同虚原子（Ghost-atoms，白色表示小分子此时与环境无相互作用:L与水解耦，即为去溶剂化）；
$C状态：L------>L_(restr)$

C状态 ：无相互作用力的小分子与蛋白结合，进入蛋白的结合口袋，形成状态Ｄ中的复合物，这里引入了限制势，限制势的引入是为了防止配体在蛋白质中乱跑（尤其是关闭了大部分配体与环境的相互作用时）、阻碍收敛，只要最后在能量加上校正项就行。

需要注意的是在关闭相互作用时，我们总是先关闭静电作用，再关闭非静电项；如果反过来的话，那就会出现这样的情况——正负电荷的原子可能会靠的无限近，这显然是不合理的。反之，如果使用的是逐步打开相互作用的途径，那就应该先打开非静电项，再打开静电项。
$D状态：P+L_{restr}------>PL(restr)$

C状态 :看上去我们似乎C到D的自由能变化，但实际上C与D的状态是完全相同的，反正此时的配体都不与周围环境有任何相互作用了，由自由能的定义可知，换个环境对自由能改变为0。
$E状态：PL------->PL_{restr+elec+vdw}$

**E状态：**L在P的结合口袋中,打开配体L与受体P之间的相互作用elec和VDW,此时ΔG为结合自由能ΔG（bind）
$F状态：PL_{restr+elec+vdw}------>PL_{elec+vdw}$

**状态Ｆ：**解除限制势L与P间的限制势，形成闭合的热力学循环，形成生物体系中的配受体复合物

因此，由Ａ直接到Ｆ变化的结合自由能 $\Delta G_(binding)$ ，可等价于由状态Ａ经状态Ｂ—Ｅ(C->D过程自由能无变化)转变为状态Ｆ过程的能量变化总和。（公式2.26所示）
$\Delta G_{binding}^0 =G_F-G_A \tag {3.8.1}$

$\Delta G_{elec+vdw}^{solv}=G_B-G_A \tag {3.8.2}$

$\Delta G_{restr}^{solv}=G_c-G_B \tag {3.8.3}$

$\Delta G=0=G_D-G_C \tag {3.8.4}$

$\Delta G_{elec+vdw}^{prot}=G_E-G_D \tag {3.8.6}$

$\Delta G_{restr}^{solv}=G_F-G_E \tag {3.8.7}$

以上（3.8.2）到（3.8.3）式相加得：
$\Delta G_{elec+vdw}^{solv}+\Delta G_{restr}^{solv}+\Delta G+\Delta G_{elec+vdw}^{prot}+\Delta G_{restr}^{solv}=G_F-G_A=\Delta G_{binding}^0 \tag {3.8.8}$
通过分别模拟小分子在溶剂水和靶蛋白的口袋中，慢慢关闭或打开小分子与环境间的相互作用（ ele和 vdw），以上两个过程构成了一个热力学循环。由于小分子与环境间相互作用的关闭（或打开）的过程是不存在的非真实物理过程，因此该计算过程也被称为“炼金术”。（使用不同的的算法来评估这一过程的变化，从而会衍生出不同的自由能计算方法，在第3节中讲到）

由上图所示，依据分子动力学模拟计算自由能的原理知，我们无需模拟配体从真空环境中到水溶剂环境中（溶剂化），然后在去溶剂化，与配体结合这一系列的过程，我们只需要取其中几个终状态，然后人为的去开关体系中的作用项即可模拟出这些过程中的变化，在本教程中主要涉及以下三个：

1.配体与溶液的解耦：A---->B状态
$\Delta G_1=\Delta G_{elec+vdw}^{solv}=G_B-G_A \tag{3.8.9}$
2.约束：B---->C状态

在解耦配体（状态B到C）上加上约束，可以用论文中的32式来分析考虑（当使用这组特定的约束时）。
$\Delta G_2=\Delta_{restr_{on}}^{solve}=RT\ln [\frac{8π^2V^0}{r_{0}^{2}sin \theta_{A,0},sin \theta_{B,0},} \frac{(K_rK_{\theta A} K_{\theta B}K_{\phi A}K_{\phi B}K_{\phi C})^{\frac{1}{2}}} {(2πkT)^3}] \tag {3.8.10}$
$R$ 为理想气体常数

$K$ 为以开尔文为单位的温度。

$V^{0}$ 为对应于一摩尔标准态（1660 $Å^{3}$ ）的体积。

$r_0$ 为是约束装置的参考距离。

$\theta_A,\theta_B$ 为是约束的参考角度。

$k_x$ 为是距离( $r_0$ )的力常数,我们应用两个角度（ $\theta_A,\theta_B$ ）和三个二面角（ $\phi A,\phi B,\phi C$ ）的限制

3.配体与受体解耦：

正常的模拟过程应该是配体与受体耦合，但是为了处理简单使用的是配体与受体已经结合在一起的模型，所以这里模拟是解耦的过程（F—>D）状态，与配体与受体结合过程（D—>F）相反，所以该过程的自由能要取反：
$\Delta G_3=-\Delta G_{elec+vdw+restr}^{prot} \tag {3.8.11}$

设置：

1.既然需要进行两个独立体系自由能计算，最后通过热力学循环来求得配体与受体之间绝对结合自由能，那么就需要去准备两套模拟配置文件：如下:

1.对于配体与溶液的解耦：A---->B状态

**01.ligand文件下的目录结构**
├── collect_dhdl.sh             :批量收集分析所需要数据的脚本
├── batche.sh                   :批量执行job_0.sh -->job_19.sh 的脚本
├── write_mdp.sh                :批量生成mdp文件的脚本，主要修改mdp 中的init_lambda_state =nlambda 的值
├── write_sh.sh                 :批量生成job文件的脚本,主要修改job文件中 LAMBDA=Wnum的值，
├── job.sh                  :为每一窗口独立运行整个模拟过程（EM->NVT->NPT->Production_MD），即Lambda_0，
├── MDP                         :总运行参数mdp文件夹
│   ├── EM                      :能量最小化参数mdp文件夹
│   │   ├── enmin.mdp            :第1次能量最小化参数mdp文件
│   │   └── write_mdp.sh        : 用法：./write_mdp.sh  enmin     
│   ├── NVT                     :等温等容预平衡参数mdp文件夹
│   │   ├── nvt.mdp             :等温等容预平衡参数mdp文件
│   │   ├── write_mdp.sh        : 用法：./write_mdp.sh  nvt     即可后接mdp文件前缀
│   ├── NPT                     :等温等压预平衡参数mdp文件夹
│   │   ├── npt.mdp             :等温等压预平衡参数mdp文件
│   │   └── write_mdp.sh        : 用法：./write_mdp.sh  npt     即可后接mdp文件前缀
│   └── Production_MD           :成品模拟参数mdp文件夹
│       ├── prod.mdp             :成品模拟参数mdp文件
│       └── write_mdp.sh        : 用法：./write_mdp.sh  prod    即可后接mdp文件前缀
├── Ligand                      :结构文件和拓扑文件夹
│   ├── ligand.gro              :含1个甲烷水盒子结构文件
│   ├── posre_ligand.itp        :约束文件
│   └── ligand.top                :体系top文件
└── REDERME.md

以为该体系enmin.mdp为例子，说明配体与溶液发生去耦合过程的自由能计算代码设置，每项具体信息见3.3

在.mdp文件中，我们定义了2个lambda向量：coulomb和vdw

;====================================================
; Energy minimization
;====================================================

;----------------------------------------------------
; RUN CONTROL & MINIMIZATION
;----------------------------------------------------
define                 = -DFLEXIBLE
integrator             = steep
nsteps                 = 5000
emtol                  = 100
emstep                 = 0.01
nstcomm                = 100

;----------------------------------------------------
; OUTPUT CONTROL
;----------------------------------------------------
nstxout                = 250        ; save coordinates to .trr every 250 steps
nstvout                = 0          ; don't save velocities to .trr
nstfout                = 0          ; don't save forces to .trr

nstxout-compressed     = 500        ; xtc compressed trajectory output every 500 steps
compressed-x-precision = 1000
nstlog                 = 500        ; update log file every 500 steps
nstenergy              = 500        ; save energies every 500 steps
nstcalcenergy          = 100

;----------------------------------------------------
; NEIGHBOR SEARCHING
;----------------------------------------------------
cutoff-scheme          = Verlet
ns-type                = grid
nstlist                = 1
rlist                  = 1.0

;----------------------------------------------------
; BONDS
;----------------------------------------------------
constraints            = none

;----------------------------------------------------
; ELECTROSTATICS
;----------------------------------------------------
coulombtype            = PME
rcoulomb               = 1.0
pme-order              = 6 
fourierspacing         = 0.10
ewald-rtol             = 1e-6

;----------------------------------------------------
; VDW
;----------------------------------------------------
vdw-type                = PME
rvdw                    = 1.0
vdw-modifier            = Potential-Shift
ewald-rtol-lj           = 1e-3
lj-pme-comb-rule        = Geometric
DispCorr                = EnerPres

;----------------------------------------------------
; TEMPERATURE & PRESSURE COUPL
;----------------------------------------------------
Tcoupl              = no
Pcoupl              = no
gen_vel             = no

;----------------------------------------------------
; FREE ENERGY CALCULATIONS
;----------------------------------------------------
free-energy              = yes
couple-moltype           = ligand
couple-lambda0           = vdw-q       ;当lambda=0（A状态），范德华和静电相互作用打开
couple-lambda1           = none        ;当lambda=1（B状态），所有作用力关闭
                                       ;  A---->B,配体与受体解耦
couple-intramol          = no
separate-dhdl-file       = yes
sc-alpha                 = 0.5
sc-power                 = 1
sc-sigma		         = 0.3
init-lambda-state        = nlambda     ;nlambda的值从0-19
coul-lambdas             = 0.0 0.25 0.5 0.75 1.0 1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.0 1.00 1.0 1.00 1.0 1.00 1.0
vdw-lambdas              = 0.0 0.00 0.0 0.00 0.0 0.05 0.1 0.2 0.3 0.4 0.5 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1.0 
nstdhdl                  = 100
calc-lambda-neighbors    = -1

3.对于配体与受体解耦：

**02.Complex文件下的目录结构**
├── collect_dhdl.sh             :批量收集分析所需要数据的脚本
├── batche.sh                   :批量执行job_0.sh -->job_19.sh 的脚本
├── write_mdp.sh                :批量生成mdp文件的脚本，主要修改mdp 中的init_lambda_state =nlambda 的值
├── write_sh.sh                 :批量生成job文件的脚本,主要修改job文件中 LAMBDA=Wnum的值，
├── job.sh                  :为每一窗口独立运行整个模拟过程（EM->NVT->NPT->Production_MD），即Lambda_0，
├── MDP                         :总运行参数mdp文件夹
│   ├── EM                      :能量最小化参数mdp文件夹
│   │   ├── enmin.mdp            :第1次能量最小化参数mdp文件
│   │   └── write_mdp.sh        : 用法：./write_mdp.sh  enmin     
│   ├── NVT                     :等温等容预平衡参数mdp文件夹
│   │   ├── nvt.mdp             :等温等容预平衡参数mdp文件
│   │   ├── write_mdp.sh        : 用法：./write_mdp.sh  nvt     即可后接mdp文件前缀
│   ├── NPT                     :等温等压预平衡参数mdp文件夹
│   │   ├── npt.mdp             :等温等压预平衡参数mdp文件
│   │   └── write_mdp.sh        : 用法：./write_mdp.sh  npt     即可后接mdp文件前缀
│   └── Production_MD           :成品模拟参数mdp文件夹
│       ├── prod.mdp             :成品模拟参数mdp文件
│       └── write_mdp.sh        : 用法：./write_mdp.sh  prod    即可后接mdp文件前缀
├── Complex                      :结构文件和拓扑文件夹
│   ├── complex.gro              :含1个甲烷水盒子结构文件
│   ├── ligand.itp               :配体拓扑文件
│   ├── posre_ligand.itp         ：约束文件
│   ├── posre_complex.itp         ：约束文件
│   └── complex.top                :体系top文件
└── REDERME.md

同样以为该体系enmin.mdp为例子，说明配体与溶液发生去耦合过程的自由能计算代码设置，每项具体信息见3.3

在.mdp文件中，我们定义了3个lambda向量：bonded，coulomb和vdw

;====================================================
; Energy minimization
;====================================================

;----------------------------------------------------
; RUN CONTROL & MINIMIZATION
;----------------------------------------------------
define                 = -DFLEXIBLE
integrator             = steep
nsteps                 = 5000
emtol                  = 100
emstep                 = 0.01
nstcomm                = 100

;----------------------------------------------------
; OUTPUT CONTROL
;----------------------------------------------------
nstxout                = 250        ; save coordinates to .trr every 250 steps
nstvout                = 0          ; don't save velocities to .trr
nstfout                = 0          ; don't save forces to .trr

nstxout-compressed     = 500        ; xtc compressed trajectory output every 500 steps
compressed-x-precision = 1000
nstlog                 = 500        ; update log file every 500 steps
nstenergy              = 500        ; save energies every 500 steps
nstcalcenergy          = 100

;----------------------------------------------------
; NEIGHBOR SEARCHING
;----------------------------------------------------
cutoff-scheme          = Verlet
ns-type                = grid
nstlist                = 1
rlist                  = 1.0

;----------------------------------------------------
; BONDS
;----------------------------------------------------
constraints            = none

;----------------------------------------------------
; ELECTROSTATICS
;----------------------------------------------------
coulombtype            = PME
rcoulomb               = 1.0
pme-order              = 6 
fourierspacing         = 0.10
ewald-rtol             = 1e-6

;----------------------------------------------------
; VDW
;----------------------------------------------------
vdw-type                = PME
rvdw                    = 1.0
vdw-modifier            = Potential-Shift
ewald-rtol-lj           = 1e-3
lj-pme-comb-rule        = Geometric
DispCorr                = EnerPres

;----------------------------------------------------
; TEMPERATURE & PRESSURE COUPL
;----------------------------------------------------
Tcoupl              = no
Pcoupl              = no
gen_vel             = no

;----------------------------------------------------
; FREE ENERGY CALCULATIONS
;----------------------------------------------------
free-energy              = yes
couple-moltype           = ligand
couple-lambda0           = vdw-q
couple-lambda1           = none
couple-intramol          = no
separate-dhdl-file       = yes
sc-alpha                 = 0.5
sc-power                 = 1
sc-sigma		 = 0.3
init-lambda-state        = nlambda     ; ;nlambda的值从0-29
bonded-lambdas           = 0.0 0.01 0.025 0.05 0.075 0.1 0.2 0.35 0.5 0.75 1.0 1.00 1.0 1.00 1.0 1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.0 1.00 1.0 1.00 1.0 1.00 1.0
coul-lambdas             = 0.0 0.00 0.000 0.00 0.000 0.0 0.0 0.00 0.0 0.00 0.0 0.25 0.5 0.75 1.0 1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.0 1.00 1.0 1.00 1.0 1.00 1.0
vdw-lambdas              = 0.0 0.00 0.000 0.00 0.000 0.0 0.0 0.00 0.0 0.00 0.0 0.00 0.0 0.00 0.0 0.05 0.1 0.2 0.3 0.4 0.5 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1.0
nstdhdl                  = 100
calc-lambda-neighbors    = -1

模拟

模拟过程参考3.3.，这里不在赘述

分析

分析过程参考3.3.,可以使用alchemical_analysis快捷分析。

根据公式3.8.8对配体与受体之间的结合自由能定义可以知：
$\begin{aligned} \Delta G_{binding}^0&=\Delta G_1+\Delta G_2+\Delta G_3 \\ &=\Delta G_{elec+vdw}^{solv}+\Delta_{restr_{on}}^{solve}-\Delta G_{elec+vdw+restr}^{prot} \end{aligned}$
其中 $\Delta G_1和\Delta G3$ 的值可以通过本例分子模计算自由能再使用alchemical_analysis工具分析得出，这里不赘述，同3.3， $\Delta G_2$ 的值可以通过公式3.8.10得出，具体见原教程1.gromacs计算结合自由能(en)

备注：

gromacs版本不同，本教程所以案例使用的是gmx 版本，请根据实际情况做修改，常见版本如下：

gmx : MD引擎二进制，没有MPI，但支持线程-MPI。如果GROMACS在一个节点上执行，以及在计算节点上运行分析工具，则非常有用。
gmx_mpi : 支持MPI的MD引擎二进制。这是研究人员最常使用的二进制。
gmx_d : 没有MPI的MD引擎双精度二进制，但支持线程-MPI。
gmx_mpi_d : 和上面一样，但是是双精度的。这个比混合精度的mdrun_mpi慢很多。
gmx_avx : 这个二进制文件在不支持AVX2的情况下产生，用于登录节点。

参考链接：

1.gromacs手册：7.3.23 自由能计算

2.gromacs手册：自由能计算的实现

3.gromacs计算结合自由能案例(en)

4.gmx bar: 利用Bennett接受比率方法计算自由能差的估计值(翻译: 陈珂)

以上所有示例模拟文件配置文件关注：“理论与计算化学初学者”公众号，回复“自由能”获得下载链接

你可能感兴趣的:(自由能)

逃避自由海岛世界
自由这个东西向来是人人把它捧在手心里的。工作者丢下一封辞职信，说山高海阔，老子追求自由去了，于是网上人人拍手点赞；无业游民聚在咖啡店里侃天侃地，和兢兢业业过日子的人说自由多么好，自由能让人寻求人生的意义。呵！信你个鬼！在我看来，自由这个东西，是用来欺骗别人，掩饰自己的。在现代，它往往是懒散的遮羞布，是井底蛙想要的乌托邦。自由明明只是心里驻扎的原野，才不是世人所期待的时间停下来的悠闲。不过不可否认，
GULP 案例 4：如何计算热力学性质（热容、熵、焓、自由能等）？ 123wxw gulp
----------------------------------------------------------------------物体的热力学性质是指物质处于平衡状态下压力P、体积V、温度T、组成以及其他的热力学函数之间的变化规律。一般将材料的压力P、体积V、温度T、内能U、焓H、熵S等统称为物体热力学性质。热力学性质一般通过第一性原理计算+准谐近似模型得到，如VASP+phononpy
圈石毅1
圈子，决定你的上层建筑，人脉决定你的信息资源。因为这几年都没有上班，靠的都是圈层，提供信息赚钱。我认为混圈子，首先自己要有圈子的价值，那么能体现圈子价值积累改变的，首先是做人！然后就有吸引法则。身上自由能量，萌发，别人觉得你好打交道！做人，是一门高深的学问。自我总结两点，不争吵，不贪便宜！遇事要冷静，不争吵，不发脾气的人，和和气气面对所有人！不贪便宜，任何人应该有恩报恩，有德报德。当你做好这点，你
约翰瑟尔的故事 xhZhangShaoFan 空间计算
约翰瑟尔的故事你即将看到的是“瑟尔效能机”创始者，约翰瑟尔的故事据瑟尔原话，该装置会是通向自由能源的关键“他”拥有“会飞”等不可思议的特性相关说法还有待证实，此记录篇仅为告知观者制片方对瑟尔技术持中立态度以下是我们所搜集到的证据，希望观者自行决定–BKL制片公司提示：写完文章后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录约翰瑟尔的故事前言一、约翰瑟尔人生旅程、装置研究以及他的语录二、使
你是怎么看待金钱的？歸無
财富自由能让我们有更大更多的选择。但大数人内心里对财富既有渴望，又有评判，以及很多的负面情绪和不如意。金钱被创造出来是用来表达欣赏和喜悦，用来呈现这个世界的美好，这是我们赋予它的一个作用。所以当我们把痛苦、无能、自责、愧疚、焦虑，觉得自己不够好这样的作用力给到财富的时候，财富自然会被推开。当一个人心轮能量波动的是沮丧、难过、自责、愧疚、愤怒、怨恨、焦虑、痛苦……几乎都会负债。如果是轻微的自责、愧疚
2022-12-29 感恩学习相信小陶
感恩！六点签到生物光子发射作用在压力状态下便会增长——这是一种防卫机制，目的是要设法让患者恢复均衡。这一切现象让波普开始思考，他认为生物光子发射具有矫正作用，这是零点能量场起伏对生命系统发挥的影响。所有系统都希望自由能量达到最低程度。理想世界里的波动全都借由破坏性干涉彼此抵消，然而针对零点能量场而言，这却不可能实现，因为场内会不断出现细微能量起伏来干扰系统。发射光子是一种补偿行为，目的是要制止这种
phonopy快速安装教程 DFT计算杂谈 linux
Phonopy是一个由python编译实现的的晶体声子分析程序，是一款基于第一性原理进行声子计算的免费软件。它提供了VASP的Wien2k接口用来计算原子受力。它的主要功能有：计算声子色散谱；计算声子态密度，包括分立态密度；晶体热力学性质，包括自由能，热容量，熵。在以往推送内容中也有介绍基于phonopy的众多使用说明，包括：VASP+phonopy计算声子群速与数据导出phonopy计算模式格林
痛苦来源于选择 Dater
今日，我在网上找工作，因为喜欢看书，所以找图书管理的工作，琳琅满目的工作映入眼帘，有书店的店员，有图书馆的管理员，有销售员，有收银员.......最终经过两个小时谈话筛选,有两个工作脱颖而出,一个西西弗书店专员,一个自助书店店员，第一个不能看书，但是社交因素多；第二个自由能看书，但是只有你一个人管理，前期还要出去发传单；我是一个害怕社交但是又知道社交的重要性的人，一整天都在两个工作的选择之间，痛苦
热力学统计物理专业英语词汇 River Chandler 物理学与工程学专业英语 python 算法数学建模抽象代数 numpy
热力学统计物理专业英语词汇work功entropy熵isobaric等压isothermal等温isochoric等容adiabatic绝热enthalpy焓freeenergy自由能surroundings外界gibbsenergy吉布斯自由能heatcapacity热容heatreservoir热源phasse相equilibrium平衡specificcapacity比热expansivit
华为服务器串号官网查询系统,查询服务器序列号 A兰舍硅藻泥华为服务器串号官网查询系统
查询服务器序列号内容精选换一换简要介绍randfold是一个独立的基因测序相关软件，它从原始序列开始随机显示其核苷酸顺序。它根据改组后的序列计算推断结构的最小自由能(MFE)，并多次重复计算以建立最小自由能(MFE)值的分布。开发语言：C一句话描述：基因序列二级结构随机测试软件开源协议：GPL2.0建议的版本建议使用最新版本，此处以randfold2.01版本为例说第三方应用在物联网平台订阅了设备
2021-09-16 imxiel
知识点分享（2021.09.18）计算氢电极与实验氢电极的联系何在？由于氢离子、电子的吉布斯自由能难以通过计算进行精确获得，计算氢电极（CHE）被Nørskov等人提出，在该模型中质子和电子的吉布斯自由能与氢气的自由能-eU等效。针对CHE，之前一直存在问题：在DFT所能模拟的尺度上，似乎看不出到电极这种宏观尺度的物体，因此实验计算氢电极来进行等效处理是否有实际意义？计算氢电极的作用何在？本期知识
16 洁喵
“一直宠着你，我的小宝贝。”一瞬间就被小哥哥戳中了呐。本来我是想行走江湖的，独立自由能力强散发女性的魅力，现在觉得为你洗手作羹汤也还蛮不错。
【共修】2018.11.2（周四）茶女子张怡
图片发自App财务自由能让我们活得更独立更有底气。现在经常看到很多人都说要佛系生活，待在舒适区里，一切随缘，不去努力。可是现实如此扎心，各种天灾人祸，若你选择佛系生活，谁替你斩妖除魔？佛系绝不是安于现状，而是尽己所能力争上游。努力或许不一定会成功，但不努力一定会失败。所以好好学习理财，争取早日实现财务自由吧～今天看到公众号，琢磨先生写的，就订购一份，不知道有没有收获，先看看。前面看了小狗钱钱我还是
冶金物理化学809,这些重点内容你掌握了吗？小小怪兽呀
一直以来，我都认为冶金物理化学809考研靠的最多的是天赋，但经过了海文考研老师们的点拨，让我了解到，再难的知识点，只要掌握了学习方法，都会变得容易的多。比如，冶金物理化学809主要参考书目——北京科技大学冶金与生态工程学院教授、博士生导师郭汉杰老师编写的-《冶金物理化学教程》第2版。冶金物理化学809复习分为6个章节：分别为第一章:绪论；第二章：冶金过程化学反应的吉布斯自由能ΔG、ΔGθ；第三章：
gromacs PCA 做自由能景观图 xiaolan39 MD perl
在文献中看到有人做自由能景观图，记录下自己的操作过程参考http://www.kangsgo.com/49.htmlhttp://sobereva.com/73https://www.zhihu.com/question/19895566跑完动力学后蛋白比对gmxtrjconv-fmd.xtc-smd.tpr-fitrot+trans-omdfit.xtc选择backbone以及system用于输
母亲的努力虫儿眠
传统家庭的母亲是家中最不起眼的角色是父亲高大身躯下弱小的影子是离家的孩子心中最难以察觉的牵挂人们能看见父亲的自由能看见孩子的活力却往往看不见背后的母亲默默地操持着一个家她容忍父亲的懒散也容忍孩子的堕落生活的重压下唯有努力方可牢牢牵住这个家母亲从未对孩子要求过什么只希望孩子能努力她照顾了孩子十几年的无忧生活但她终究会有再也照顾不了的那一天当她的努力到了尽头只希望孩子继续努力她才好放心你为什么不努力这
掌控人生，从掌控习惯开始珍珍日上的小郎
“生命诚可贵，爱情价更高，若为自由故，两者皆可抛！”追求自由能掌控自己的人生是每个人的渴望，但很少有人能够按自己的想法过完一生！比如很多人都想养成阅读、健身等好习惯，也有很多人想戒掉抽烟、酗酒等坏习惯，但我们经常会半途而废。最终屈于自己的惰性、没毅力或环境，为何好习惯如此“难养”？为何坏习惯如此难戒？读过《掌控习惯》这本书，你就会知道，不是我们决心不够，而是没有找对方法。《掌控习惯》作者是美国著名
读书语芯静然
读书读书，为有能力选择更好生活，为有尊严的人格以找到真善美，为更广阔的天空，为有力能感恩爱自己及自己爱的人。为有能力选择更好生活！若辜负了青春，若未好好在最好的校园时光读书，生命的选择权严重减低，读书人可以选择在有空调的写字楼工作，不读书人的无选择只能被动逼迫自己做别人选剩下的最下层，最繁重，最体力，最廉价你不愿做的工作。工作没有高低，但读书给了你生命的自由能选择自己喜欢的工作。为了有尊严人格！读
假如自由能分七个等级，第六名是搬家，最高级竟然是这个！小丰搬家碎片
小时候想着长大一定要有车有房，出国旅行，好好享受自由的生活，可没想到等到长大以后发现自己裤兜里连点外卖都要货比三家找个价格不超过20块的。更别提什么环游世界了，这两年连本省都没有出去过，毕竟出去一趟半年工资就没了。有钱人的游戏，我等这些穷人玩不起呀。前段时间猪肉价格暴涨让人望而却步、车厘子自由让吃水果成为奢望，到如今蔬菜都吃不起，原来活着本来就是一件不容易的事情，每一种东西的自由索取都需要资本的支
给自己的时间做个体检珍姐_10b4
你实现了精力自由吗？你们知道一个理想的生活模式是怎样的吗？应该是通过“心流”和“放空”的交替来掌控自己的时间和注意力！这也就是精力自由！精力自由能够摒弃和无视外在的种种干扰，尽可能减少其他事务，把自己的注意力（准星）最大限度地集中在核心价值上。核心价值是指代表那些最重要，能提现我们独一无二价值的事情。做到精力自由需要满足两个要求：1.知道自己想要什么即能够清晰地勾勒出自己的“核心价值”2.具备控制
能流进化论——在外星球上发现生命所必需的物质就能意味着存在地外生命吗？ dream0711
要回答这个问题，首先应该明白地球上为什么会存在生命？或者说生命为什么会在地球上出现？通过对生命体的观察不难发现，所有生命体都需要食物和氧气（有的生物可能需要其它种类的氧化性物质）。食物在生命体内经过一系列的生物化学反应，被一步步转化为能量相对较低的化学物质，同时释放出自由能和热。基于此，食物在生命体内的代谢过程，可以认为是食物中的能量被生命体释放和传递的过程。在这个过程中，生命体作为介体起释放和传
晨间日记钰见
万般皆为贫，唯有自由高！今天能上班了真好，平常感觉不到空气、平安、健康、亲情、友情、自由等美好的可贵，失去一次再拥有，就感觉非常珍贵！世上最大的喜悦莫过于失而复得，突然被封，没了自由，还带着“阳了”恐惧，让人坐卧不安、心神不宁，主要也怕传染家人，中年人的危机害怕把家人带到坑里……去冒险。没事了，今天心情格外舒畅，看什么都美好，从获自由能量满满当当！
再出发以终为始不负韶华
又一年多少人在无力改变的现实面前选择了无欲无求实为病态是人就有需求欲望无欲无求只是迷茫的外衣是没有找到真正的热爱l世间能有几人不是结果的奴隶对常人而言没有金钱的自由何来身心的自由是的我们皆常人可有金钱的自由也未必身心自由能做什么若能选你所爱，很好更要爱你所选，才好对选择，敬畏，痴迷人生是酒需要时间的积累与沉淀才能喝起来酣畅淋漓而唯有热爱才能配得上时间热爱不是三分钟热情没有如烟火般的灿烂它只是默默播
羊肉价格连涨7周，牛羊肉每公斤超74元，吃肉自由能回来吗？慕容随风
在中国有句古话叫做民以食为天，每天吃什么相信都是国人最纠结的问题，然而最近我们看到的几组数据却让吃货们有点开心不起来了，这是因为大家的吃肉自由好像又要少了点，面对着牛羊肉价格的上涨，面对着猪肉价格的连涨，我们到底该怎么看？吃肉自由什么时候能回来？一、接连涨价的猪牛羊肉根据央视财经的报道，临近春节，猪牛羊等肉类价格又开始出现上涨，其中牛、羊肉价格连续刷了新高。数据显示，截至2021年第1周，羊肉批发
机器学习 | Python实现NARX模型预测控制机器学习之心 #NAR和NARX神经网络机器学习 NARX 模型预测控制
机器学习|Python实现NARX模型预测控制目录机器学习|Python实现NARX模型预测控制效果一览基本介绍研究内容程序设计参考资料效果一览基本介绍机器学习|Python实现NARX模型预测控制研究内容贝叶斯黑盒模型预测控制，基于具有外源输入的非线性自回归模型的预期自由能最小化代理。程序设计主程序usingReviseusingForwardDiffusingOptimusingRxInfer
模拟退火模型 WangXinmingg
什么是退火：退火是指将固体加热到足够高的温度，使分子呈随机排列状态，然后降温使之冷却，最后分子以低能状态排列，固体达到某种稳定状态。物理退火过程加温过程——增强粒子的热运动，消除系统原先可能存在的非均匀态。等温过程——对于与环境换热而温度不变的封闭系统，系统状态的自发变化总是朝自由能减少的方向进行，当自由能达到最小时，系统达到平衡态。冷却过程——使粒子热运动减弱并趋于有序，系统能量逐渐下降，从而得
全职宝妈4年，赚到人生第一桶金咖啡小调
我，89年双鱼座，33岁，二胎宝妈。大宝4岁半，小宝二岁半，生完大宝的月子里开始接触清货特卖，如今4年多。一人带着俩娃，承担自己和两个孩子的所有开销，老公创业让他自顾自，没找他拿过一分钱，靠我自己依旧攒下了近20个w。我的心得就是，多靠近有结果的，积极果敢的人。不给自己设限，做就对了，纠结焦虑无意，远离负能量。为何选择做清货？时间自由能顾娃顾家，还能赚米跟宝妈们一样，我的时间是琐碎的，大多数时间是
2021年3月1日反省和精进联智生活家冯腾
自律才能自由能量的提升需要内心有爱，利他是这个世界最美好的事情，也是最伟大的力量。做任何事都要建立自己的基本套路，因为所有高手都是持续练习基本套路并获得反馈的结果，才会持续变成高手。到此觉悟，以后一定要建立自己的基本套路，然后不断刻意练习优化反馈。一个人的语言是有能量的，如果能结合语音语调+肢体动作，还有反问句，利他之心，就能改变人的心智，震撼人的灵魂！学习演讲的三大信念安静下来，练习基本套路，人
冶金物理化学809,这些重点内容你掌握了吗？ shan0719
一直以来，我都认为冶金物理化学809考研靠的最多的是天赋，但经过了海文考研老师们的点拨，让我了解到，再难的知识点，只要掌握了学习方法，都会变得容易的多。比如，冶金物理化学809主要参考书目——北京科技大学冶金与生态工程学院教授、博士生导师郭汉杰老师编写的-《冶金物理化学教程》第2版。冶金物理化学809复习分为6个章节：分别为第一章:绪论；第二章：冶金过程化学反应的吉布斯自由能ΔG、ΔGθ；第三章：
一文！解决静电场能量的计算和推导严正安电磁场科技服务器机器学习 javascript 前端
目录引言经典能量点电荷系统连续电荷分布系统中的经典能量静电能量的分布及其密度例题思考引言电场对静止电荷有力的作用，对运动的电荷则要做功。可见静电场中存储着能量，把静电场中的储能称之为静电能量。从另一个角度来看，静电能量是电场在建立过程中外源搬运电荷所做的功的总和经典能量点电荷系统我们先考虑有三个点电荷的系统，下面是详细的推导其中静电场能量我们只包含了互有能，没有包含自由能自由能的产生也很容易理解，
如何用ruby来写hadoop的mapreduce并生成jar包 wudixiaotie mapreduce
ruby来写hadoop的mapreduce，我用的方法是rubydoop。怎么配置环境呢： 1.安装rvm：不说了网上有 2.安装ruby：由于我以前是做ruby的，所以习惯性的先安装了ruby，起码调试起来比jruby快多了。 3.安装jruby： rvm install jruby然后等待安
java编程思想 -- 访问控制权限百合不是茶 java 访问控制权限单例模式
访问权限是java中一个比较中要的知识点,它规定者什么方法可以访问,什么不可以访问一:包访问权限; 自定义包: package com.wj.control; //包 public class Demo { //定义一个无参的方法 public void DemoPackage(){ System.out.println("调用
[生物与医学]请审慎食用小龙虾 comsci 生物
现在的餐馆里面出售的小龙虾,有一些是在野外捕捉的,这些小龙虾身体里面可能带有某些病毒和细菌,人食用以后可能会导致一些疾病,严重的甚至会死亡..... 所以,参加聚餐的时候,最好不要点小龙虾...就吃养殖的猪肉,牛肉,羊肉和鱼,等动物蛋白质
org.apache.jasper.JasperException: Unable to compile class for JSP: 商人shang maven 2.2 jdk1.8
环境： jdk1.8 maven tomcat7-maven-plugin 2.0 原因： tomcat7-maven-plugin 2.0 不知吃 jdk 1.8，换成 tomcat7-maven-plugin 2.2就行，即 <plugin>
你的垃圾你处理掉了吗?GC oloz GC
前序:本人菜鸟，此文研究学习来自网络，各位牛牛多指教　 1.垃圾收集算法的核心思想　　Java语言建立了垃圾收集机制，用以跟踪正在使用的对象和发现并回收不再使用(引用)的对象。该机制可以有效防范动态内存分配中可能发生的两个危险：因内存垃圾过多而引发的内存耗尽，以及不恰当的内存释放所造成的内存非法引用。　　垃圾收集算法的核心思想是：对虚拟机可用内存空间，即堆空间中的对象进行识别
shiro 和 SESSSION 杨白白 shiro
shiro 在web项目里默认使用的是web容器提供的session，也就是说shiro使用的session是web容器产生的，并不是自己产生的，在用于非web环境时可用其他来源代替。在web工程启动的时候它就和容器绑定在了一起，这是通过web.xml里面的shiroFilter实现的。通过session.getSession()方法会在浏览器cokkice产生JESSIONID，当关闭浏览器，此
移动互联网终端淘宝客如何实现盈利小桔子移動客戶端淘客淘寶App
2012年淘宝联盟平台为站长和淘宝客带来的分成收入突破30亿元，同比增长100%。而来自移动端的分成达1亿元，其中美丽说、蘑菇街、果库、口袋购物等App运营商分成近5000万元。可以看出，虽然目前阶段PC端对于淘客而言仍旧是盈利的大头，但移动端已经呈现出爆发之势。而且这个势头将随着智能终端(手机，平板)的加速普及而更加迅猛
wordpress小工具制作 aichenglong wordpress 小工具
wordpress 使用侧边栏的小工具，很方便调整页面结构小工具的制作过程 1 在自己的主题文件中新建一个文件夹(如widget)，在文件夹中创建一个php(AWP_posts-category.php) 小工具是一个类,想侧边栏一样，还得使用代码注册，他才可以再后台使用，基本的代码一层不变 <?php class AWP_Post_Category extends WP_Wi
JS微信分享 AILIKES js
// 所有功能必须包含在 WeixinApi.ready 中进行 WeixinApi.ready(function(Api) { // 微信分享的数据 var wxData = { &nb
封装探讨百合不是茶 JAVA面向对象封装
//封装属性方法将某些东西包装在一起，通过创建对象或使用静态的方法来调用，称为封装；封装其实就是有选择性地公开或隐藏某些信息，它解决了数据的安全性问题，增加代码的可读性和可维护性在 Aname类中申明三个属性，将其封装在一个类中：通过对象来调用例如 1： //属性将其设为私有姓名 name 可以公开
jquery radio/checkbox change事件不能触发的问题 bijian1013 JavaScript jquery
我想让radio来控制当前我选择的是机动车还是特种车，如下所示： <html> <head> <script src="http://ajax.googleapis.com/ajax/libs/jquery/1.7.1/jquery.min.js" type="text/javascript"><
AngularJS中安全性措施 bijian1013 JavaScript AngularJS 安全性 XSRF JSON漏洞
在使用web应用中，安全性是应该首要考虑的一个问题。AngularJS提供了一些辅助机制，用来防护来自两个常见攻击方向的网络攻击。一.JSON漏洞当使用一个GET请求获取JSON数组信息的时候（尤其是当这一信息非常敏感，
[Maven学习笔记九]Maven发布web项目 bit1129 maven
基于Maven的web项目的标准项目结构 user-project user-core user-service user-web src
【Hive七】Hive用户自定义聚合函数(UDAF) bit1129 hive
用户自定义聚合函数，用户提供的多个入参通过聚合计算(求和、求最大值、求最小值)得到一个聚合计算结果的函数。问题：UDF也可以提供输入多个参数然后输出一个结果的运算，比如加法运算add(3，5)，add这个UDF需要实现UDF的evaluate方法,那么UDF和UDAF的实质分别究竟是什么？ Double evaluate(Double a, Double b)
通过 nginx-lua 给 Nginx 增加 OAuth 支持 ronin47
前言：我们使用Nginx的Lua中间件建立了OAuth2认证和授权层。如果你也有此打算，阅读下面的文档，实现自动化并获得收益。SeatGeek 在过去几年中取得了发展，我们已经积累了不少针对各种任务的不同管理接口。我们通常为新的展示需求创建新模块，比如我们自己的博客、图表等。我们还定期开发内部工具来处理诸如部署、可视化操作及事件处理等事务。在处理这些事务中，我们使用了几个不同的接口来认证： &n
利用tomcat-redis-session-manager做session同步时自定义类对象属性保存不上的解决方法 bsr1983 session
在利用tomcat-redis-session-manager做session同步时，遇到了在session保存一个自定义对象时，修改该对象中的某个属性，session未进行序列化，属性没有被存储到redis中。在 tomcat-redis-session-manager的github上有如下说明： Session Change Tracking As noted in the &qu
《代码大全》表驱动法-Table Driven Approach-1 bylijinnan java 算法
关于Table Driven Approach的一篇非常好的文章： http://www.codeproject.com/Articles/42732/Table-driven-Approach package com.ljn.base; import java.util.Random; public class TableDriven { public
Sybase封锁原理 chicony Sybase
昨天在操作Sybase IQ12.7时意外操作造成了数据库表锁定，不能删除被锁定表数据也不能往其中写入数据。由于着急往该表抽入数据，因此立马着手解决该表的解锁问题。无奈此前没有接触过Sybase IQ12.7这套数据库产品，加之当时已属于下班时间无法求助于支持人员支持，因此只有借助搜索引擎强大的
java异常处理机制 CrazyMizzz java
java异常关键字有以下几个，分别为 try catch final throw throws 他们的定义分别为 try： Opening exception-handling statement. catch： Captures the exception. finally： Runs its code before terminating
hive 数据插入DML语法汇总 daizj hive DML 数据插入
Hive的数据插入DML语法汇总1、Loading files into tables语法：1) LOAD DATA [LOCAL] INPATH 'filepath' [OVERWRITE] INTO TABLE tablename [PARTITION (partcol1=val1, partcol2=val2 ...)]解释：1)、上面命令执行环境为hive客户端环境下： hive>l
工厂设计模式 dcj3sjt126com 设计模式
使用设计模式是促进最佳实践和良好设计的好办法。设计模式可以提供针对常见的编程问题的灵活的解决方案。工厂模式工厂模式（Factory）允许你在代码执行时实例化对象。它之所以被称为工厂模式是因为它负责“生产”对象。工厂方法的参数是你要生成的对象对应的类名称。 Example #1 调用工厂方法（带参数） <?phpclass Example{
mysql字符串查找函数 dcj3sjt126com mysql
FIND_IN_SET(str,strlist) 假如字符串str 在由N 子链组成的字符串列表strlist 中，则返回值的范围在1到 N 之间。一个字符串列表就是一个由一些被‘,’符号分开的自链组成的字符串。如果第一个参数是一个常数字符串，而第二个是type SET列，则 FIND_IN_SET() 函数被优化，使用比特计算。如果str不在strlist 或st
jvm内存管理 easterfly jvm
一、JVM堆内存的划分分为年轻代和年老代。年轻代又分为三部分：一个eden,两个survivor。工作过程是这样的：e区空间满了后，执行minor gc，存活下来的对象放入s0, 对s0仍会进行minor gc，存活下来的的对象放入s1中，对s1同样执行minor gc，依旧存活的对象就放入年老代中；年老代满了之后会执行major gc，这个是stop the word模式，执行
CentOS-6.3安装配置JDK-8 gengzg centos
JAVA_HOME=/usr/java/jdk1.8.0_45 JRE_HOME=/usr/java/jdk1.8.0_45/jre PATH=$PATH:$JAVA_HOME/bin:$JRE_HOME/bin CLASSPATH=.:$JAVA_HOME/lib/dt.jar:$JAVA_HOME/lib/tools.jar:$JRE_HOME/lib export JAVA_HOME
【转】关于web路径的获取方法 huangyc1210 Web 路径
假定你的web application 名称为news,你在浏览器中输入请求路径： http://localhost:8080/news/main/list.jsp 则执行下面向行代码后打印出如下结果： 1、 System.out.println(request.getContextPath()); //可返回站点的根路径。也就是项
php里获取第一个中文首字母并排序远去的渡口数据结构 PHP
很久没来更新博客了，还是觉得工作需要多总结的好。今天来更新一个自己认为比较有成就的问题吧。最近在做储值结算，需求里结算首页需要按门店的首字母A-Z排序。我的数据结构原本是这样的： Array ( [0] => Array ( [sid] => 2885842 [recetcstoredpay] =&g
java内部类 hm4123660 java 内部类匿名内部类成员内部类方法内部类
　在Java中，可以将一个类定义在另一个类里面或者一个方法里面，这样的类称为内部类。内部类仍然是一个独立的类，在编译之后内部类会被编译成独立的.class文件，但是前面冠以外部类的类名和$符号。内部类可以间接解决多继承问题,可以使用内部类继承一个类，外部类继承一个类，实现多继承。 &nb
Caused by: java.lang.IncompatibleClassChangeError: class org.hibernate.cfg.Exten zhb8015
maven pom.xml关于hibernate的配置和异常信息如下，查了好多资料，问题还是没有解决。只知道是包冲突，就是不知道是哪个包....遇到这个问题的分享下是怎么解决的。。 maven pom: <dependency> <groupId>org.hibernate</groupId> <ar
Spark 性能相关参数配置详解－任务调度篇 Stark_Summer spark cache cpu 任务调度 yarn
随着Spark的逐渐成熟完善, 越来越多的可配置参数被添加到Spark中来, 本文试图通过阐述这其中部分参数的工作原理和配置思路, 和大家一起探讨一下如何根据实际场合对Spark进行配置优化。由于篇幅较长，所以在这里分篇组织，如果要看最新完整的网页版内容，可以戳这里：http://spark-config.readthedocs.org/，主要是便
css3滤镜 wangkeheng html css
经常看到一些网站的底部有一些灰色的图标，鼠标移入的时候会变亮，开始以为是js操作src或者bg呢，搜索了一下，发现了一个更好的方法：通过css3的滤镜方法。 html代码： <a href='' class='icon'><img src='utv.jpg' /></a> css代码： .icon{-webkit-filter: graysc