任何事物和人都不是以个体存在的,它们都被复杂的关系链所围绕着,具有一定的相关性,也会具备一定的因果关系,(比如:父母和子女,不仅具备相关性,而且还具备因果关系,因为有了父亲和母亲,才有了儿子或女儿),但不是所有相关联的事物都具备因果关系。
下面用SPSS采用回归—线性分析的方式来分析一下:居民总储蓄 和 “居民总消费”情况是否具备相关性,如果具备相关性,那相关关系的密切程度为多少。
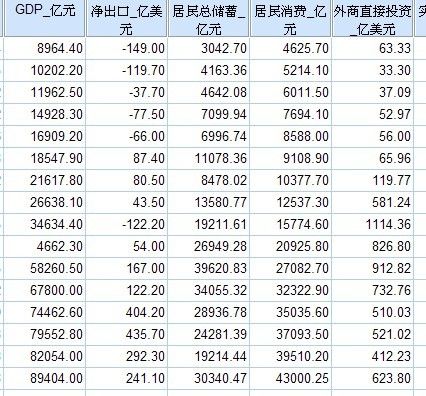
下面以“居民总储蓄”和“居民总消费”的调查样本做统计分析,数据如下所示:
第一步:我们先来分析“居民总储蓄”和“居民总消费”是否具备相关性 (采用SPSS 19版本)
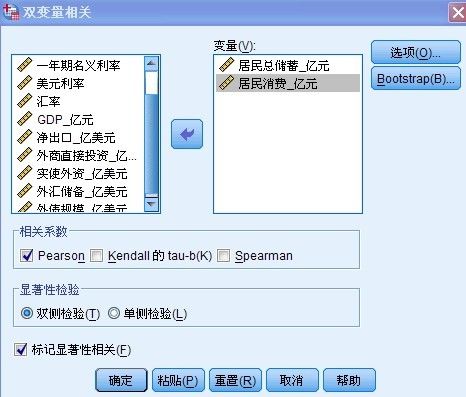
1:点击“分析”—相关—双变量, 进入如下界面:
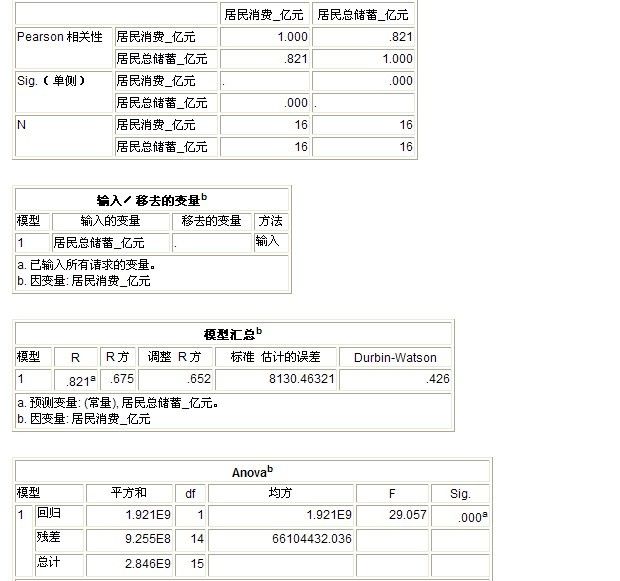
将“居民总储蓄”和“居民总消费”两个变量移入“变量”框内,在“相关系数”栏目中选择“Pearson",(Pearson是一种简单相关系数分析和计算的方法,如果需要进行进一步分析,需要借助“多远线性回归”分析)在“显著性检验”中选择“双侧检验”并且勾选“标记显著性相关”点击确定, 得到如下结果:
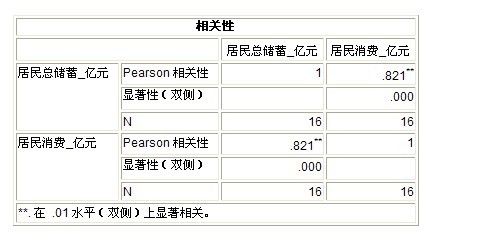
从以上结果,可以看出“Pearson"的相关性为0.821,(可以认为是“两者的相关系数为0.821)属于“正相关关系”同时“显著性(双侧) 结果为0.000, 由于0.000<0.01,所以具备显著性,得出:“居民总储蓄”和“居民总消费”具备相关性,有关联。
既然具备相关性,那么我们将进一步做分析, 建立回归分析,并且构建“一元线性方程”,如下所示:
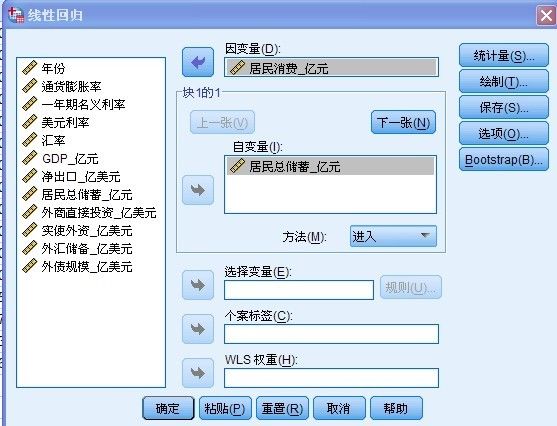
点击“分析”--回归----线性” 结果如下所示:
将“因变量”和“自变量”分别拖入框内 (如上图所示)从上图可以看出:“自变量”指 “居民总储蓄” , "因变量”是指“居民总消费”
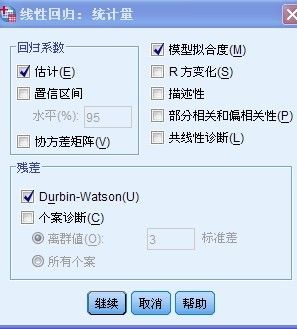
点击“统计量”进入如下界面:
在“回归系数”中选择“估计” 在右边选择“模型拟合度” 在残差下面选择“Durbin-watson(u), 点击继续按钮
再点击“绘制图”在“标准化残差图”下面选择“正太概率分布图”选项
再点击“保存”按钮,在残差下面选择“未标准化”(数据的标准化,方法有很多,这里不介绍啦)
得到如下结果:
结果分析如下:
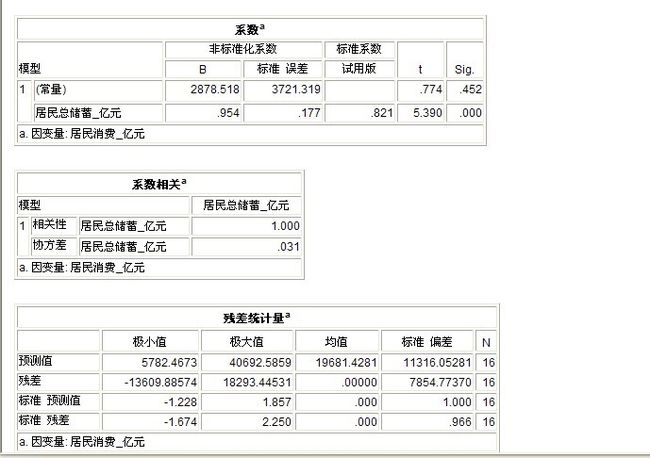
1:从模型汇总b 中可以看出“模型拟合度”为0.675,调整后的“模型拟合度”为0.652,就说明“居民总消费”的情况都可以用该模型解释,拟合度相对较高
2:从anvoa b的检验结果来看 (其实这是一个“回归模型的方差分析表)F的统计量为:29.057,P值显示为0.000,拒绝模型整体不显著的假设,证明模型整体是显著的
3:从“系数a”这个表可以看出“回归系数,回归系数的标准差,回归系数的T显著性检验 等,回归系数常量为:2878.518,但是SIG为:0.452,常数项不显著,回归系数为:0.954,相对的sig为:0.000,具备显著性,由于在“anvoa b”表中提到了模型整体是“显著”的
所以一元线性方程为:居民总消费=2878.518+0.954*居民总储蓄
其中在“样本数据统计”中,随即误差 一般叫“残差” :
从结果分析来看,可以简单的认为:居民总储蓄每增加1亿,那居民总消费将会增加0.954亿
提示:对于回归参数的估计,一般采用的是“最小二乘估计法”原则即为:“残差平方和最小“