概率论基础

组合和排列
当需要从N个物体中选取n个物体，可以通过组合公式计算出可能的结果数量。

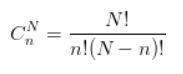
排列是组合的特殊情况，当要考虑选取的顺序时，相同的n个物体，因为不同的顺序会有不同的结果，公式变为：

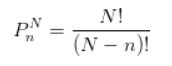
在Excel的函数中，COMBIN和PERMUT函数分别对应组合和排列。

事件及概率
定义样本空间S={(正面,正面),(反面,反面),(正面,反面),(反面,正面)},表示某个过程中可能的所有样本点
定义事件为：至少有一次正面朝上，则该事件是样本空间S的子集，即{(正面,正面),(正面,反面),(反面,正面)}，概率为75%。
通常，如果能确定一个试验的所有样本点并且能够知晓每个样本点的概率，那么我们就能求出事件的概率。

加法公式：P(A∪B) = P(A)+P(B) - P(A∩B)
互斥事件：P(A∪B) = P(A)+P(B)
条件概率：

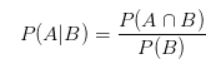
橙色圆表示事件B已经发生，如果想要知道B已经发生的情况下事件A发生的概率，则只能考虑橙色圆和蓝色元的交集部分即P(A∩B)。此时P(A∩B) 除以P(B)即给定条件B下事件A发生的概率。

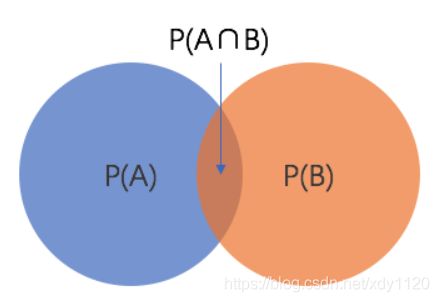
独立事件：某一事件完全不受另外事件的影响则为独立事件
如果事件A和事件B相互独立，则P(A|B)=P(A)

互斥事件和独立事件不是一回事，独立事件是完全不相关的情况，而互斥是某一事件发生另外一个事件必然不发生，它们是相关的。

贝叶斯：
用来描述两个或多个条件概率之间的关系。
按照乘法法则:
P(A∩B)=P(A)*P(B|A)=P(B)*P(A|B)
导出
P(B|A)=P(A|B)*P(B)/P(A)
或
P(A|B)=P(B|A)*P(A)/P(B)
这里只有一个事件A导致了B的发生

当有多个A导致事件B发生时，即把A拆分，

即 P(B)=P(A1)*P(B|A1)+P(A2)*P(B|A2)+…+P(An)*P(B|An)

所以：
P(Ai|B)=P(B|Ai)*P(Ai)/P(A1)*P(B|A1)+P(A2)*P(B|A2)+…+P(An)*P(B|An)

对于变量有二个以上的情况，贝式定理亦成立。例如:

P(A|B,C)=P(B|A)*P(A)*P(C|A,B)/(P(B)*P(C|B))

概率空间的三要素（Ω，F，P）
1、Ω－Sample space 样本空间，试验中所有可能结果的集合。（注：每个结果需要互斥，所有可能结果必须被穷举）
2、F－Set of events 事件集合，是[公式]的一些子集构成的集合。
3、P－Probability measure 概率测度（或概率），描述一次随机试验中被包含在Ω中的所有事件的可能性。
理解概率空间的三要素
概率论由赌博发展而来，所以用开桌赌钱作例子来讲会比较直观。
1、Ω 主要讨论的是用什么赌具，也就是赌桌上最根本的随机性来自于什么。如果用骰子的话Ω 就是骰子的六面，如果用扑克牌的话那就是52张牌，用手的话就是各种手势 ✌ ……
2、F 讨论的是赌法，也就是骰子的玩法或者扑克的打法。你是赌大小？赌谁能抓到同花顺？还是玩剪刀石头布？F 集合就是收录这些玩法组合用的，它直接构建在 Ω 上面，也就是有了赌具 Ω 才能谈赌法 F. 这个应该不难理解。
3、P 讲的是胜算，或者概率、赔率、度量……等等一个意思。 P 集合存在的意义是为了做到“精打细算”，它用一个 0-1之间的精确数值来表示赌法 F 中每种玩法的胜算。这个概念其实是帮助赌博下注的，因为有了数字的度量就能比较大小，概率大的就容易赢。

随机变量：
概率中通常将试验的结果称为随机变量，随机变量将每一个可能出现的试验结果赋予了一个数值，包含离散型随机变量和连续型随机变量。
1、随机变量无法求解
2、通常用大写字母表示，如X，为了和传统的可求解的变量区分开(如x+3=8)
3、随机变量其实是一种函数，将随机过程映射到实际数字。

比如量化一个随机过程，明天是否下雨。定义一个随机变量X，如果明天下雨X=1，如果明天不下雨X=0。
定义一个随机变量X=骰子抛出的数值，用来量化这个随机过程。

4、分为离散随机变量和连续随机变量

连续的例子：X定义为明天雨量的英寸数，描述这个可能值有无穷个数值。

概率分布 和 概率密度函数：
既然随机变量可以取不同的值，统计学家就用概率分布描述随机变量取不同值的概率。相对应的，有离散型概率分布和连续型概率分布。
连续型概率分布的概率函数也叫概率密度函数。
随机变量Y=明天雨量英寸数
横轴表示随机变量即雨量英寸数 纵轴表示概率分布，曲线表示概率密度函数。
p(Y=2) = 0,由于连续的概率密度函数，单个值出现的概率为0.
p(1 所以：曲线下方面积总计 = 1。即(0,正无穷)区间积分 = 1。概率最大不能超过1.

伯努利分布：
伯努利分布是一种离散型的概率分布
它有两种可能的结果，把一种称为成功，另外一种称为失败
每次试验成功的概率均是相同的，记录为p；失败的概率也相同，为1-p。每次试验必须相互独立。
也叫做伯努利试验

二项分布：
重复n次伯努利试验即二项概率。
已知某件事情发生的概率是p，那么做n次试验，事情发生的次数就服从于二项分布。
二项分布的公式：

掷硬币就是一个典型的二项分布。当我们要计算抛硬币n次，恰巧有x次正面朝上的概率，可以使用此公式。
假设抛硬币5次，恰巧有3次正面朝上，则其概率为31.25%。
可以使用Excel中的BINOM.DIST函数计算

泊松概率分布：
主要用于估计某事件在特定时间或空间中发生的次数。比如一天内中奖的个数，一个月内某机器损坏的次数等
泊松概率的成立条件是在任意两个长度相等的区间中，时间发生的概率是相同的，并且事件是否发生都是相互独立的。
x代表发生x次，u代表发生次数的数学期望，概率函数为：

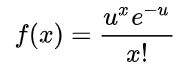
泊松分布是二项分布n很大而p很小时的一种极限形式
以卖馒头为例：
为了保证在一个时间段内只会发生“卖出、没卖出”，干脆把时间切成[公式] 份：

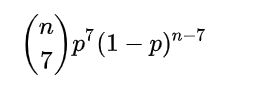
用极限表示：

更抽象一点，[公式] 时刻内卖出[公式] 个馒头的概率为：

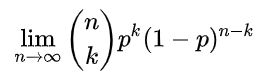
在上面的假设下，问题已经被转为了二项分布。二项分布的期望为：

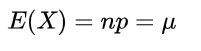
那么：

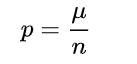
有了[公式] 了之后，就有：


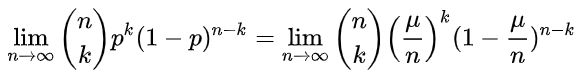
上面就是泊松分布的概率密度函数，也就是说，在[公式] 时间内卖出[公式] 个馒头的概率为：

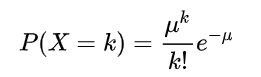
一般来说，我们会换一个符号，让[公式] ，所以：

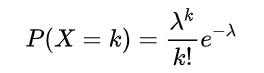
在这个例子里，期望可以利用 均值来近似。

正态分布
连续随机变量的取值是可以无限分割的，它取某个值时概率近似于0。连续变量是随机变量在某个区间内取值的概率，此时的概率函数叫做概率密度函数。
正态概率密度函数为：

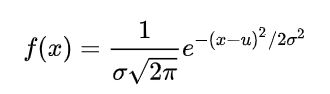
u代表均值，σ代表标准差，两者不同的取值将会造成不同形状的正态分布
均值表示正态分布的左右偏移，标准差决定曲线的宽度和平坦，标准差越大曲线越平坦
均值u=0，标准差σ=1的正态分布叫做标准正态分布。
将均值和标准差代入正态概率密度函数，得到一个简化的公式：

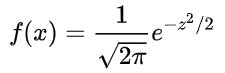
累计分布函数
它是概率密度函数的积分，累计函数就是区间概率，曲线与X轴的面积。
用P(X<=x)表示随机变量小于或者等于某个数值的概率，F(x) = P(X<=x)。
曲线就是概率密度函数，当x取某个值时，曲线上f(x)点的数值即表示随机变量在对应的x点值的取值概率，曲线与X轴相交的阴影面积就是累计分布函数。我们不妨把概率密度函数按其名字简单理解成「密度」，毕竟连续变量只有在区间中才有计算的意义，于是密度函数充当了辅助计算的角色。分析中我们更多实用累计分布函数。
当我们具有一个任意均值的u和标准差σ，都能将其转换成标准状态分布。

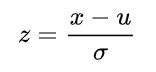
现在有一个u=10和σ=2的正态随机变量，求x在10与14之间的概率是多少？

当x=10时，z=(10-10)/2=0。当x=14时，z=(14-10)/2=2。于是x在10和14之间的概率等价于标准正态分布中0和2之间的概率。
计算P(0<=z<=2) =P(z<=2) - P(z<=0) =0.4772。

数学期望：
数学期望E（x）完全由随机变量X的概率分布所确定，若X服从某一分布，也称E（x）是这一分布的数学期望。
数学期望的定义是实验中每次可能的结果的概率乘以其结果的总和。
离散型随机量的数学期望
定义：离散型随机变量的所有可能取值 xixi 与其对应的概率 P(xi) 乘积的和为该离散型随机量的数学期望，记为 E(X)。
连续型随机量的数学期望
定义：假设连续型随机变量 XX的概率密度函数为 f(x)，如果积分∫+∞−∞xf(x)dx绝对收敛，则称这个积分的值为连续型随机量的数学期望，记为 E(X)。
数学期望的性质
设C为常数： E©==C
设C为常数： E(CX)==CE(X)
加法：E(X+Y)==E(X)+E(Y)

中心极限定理
中心极限定理指的是给定一个任意分布的总体。我每次从这些总体中随机抽取 n 个抽样，一共抽 m 次。 然后把这 m 组抽样分别求出平均值。 这些平均值的分布接近正态分布。
1、总体本身的分布不要求正态分布
2、样本每组要足够大，但也不需要太大，每组大于等于30个，即可让中心极限定理发挥作用。