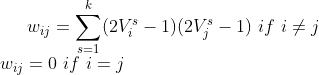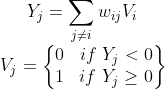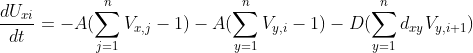Hopfield神经网络(HNN)详解
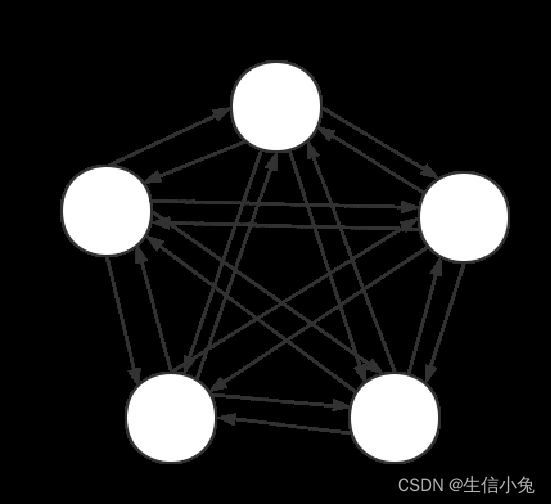
Hopfield神经网络是一种比较特殊的网络,它不像一般的神经网络那样有输入层和输出层,并且通过训练来改变神经网络中的参数,最终实现预测、识别等功能。Hopfield网络只有一群神经元节点,所有节点之间相互连接,形式如下:
虽然有些文章会画出像深度神经网络那样有输入输出的图,并且输出后又返回输入,但本质上就是多个节点之间的全连接,也就是上面的图形。Hopfield神经网络主要有两个应用:一是起到类似储存器的作用,也就是我们把多个序列或图片输入这个网络,最终这个网络会以神经元之间连接权重的形式储存这些信息,当我们再次往这个网络输入相同或有些破损部分的原来的一个输入序列/图像,它能够把序列/图像还原(恢复)回来;另一个应用就是求解TSP问题,也就是寻找最优解。
基本原理
我们先以一个简单的,只有三个神经元的Hopfield网络为例,令这三个神经元为A,B,C,其图形如下所示:
其中箭头表示从一个神经元到另一个神经元相连,每个箭头都表示相应的权重,为一个数,可以用Wij来表示。神经元自己和自己也有连接,只不过数值始终是0,所有这里没有画出。
这样我们就可以用一个矩阵来表示各个神经元之间的连接了。
| A | B | C | |
| A | 0 | ||
| B | 0 | ||
| C | 0 |
所以,Hopfield关键还是在于求权重矩阵,针对两种问题,兔兔在下面分别讨论。
基本原理与算法实现
(1)储存信息
对于储存信息,例如几个长度为n的序列,那么我们就需要一个有n个节点的神经元的神经网络来储存;如果是几个nxn维的图像矩阵,我们可以把矩阵展开成长度为![]() 的序列,再输入到神经网络中。兔兔下面以储存两个6x6维的图像为例。
的序列,再输入到神经网络中。兔兔下面以储存两个6x6维的图像为例。
第一个图像矩阵为:
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 |
图像为:
第二个图像矩阵为:
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 |
图像为:
我们把第一个矩阵展开成序列,按行按列都是可以的,不过需要统一。兔兔这里按行展开,得序列1为:[0,0,1,1,0,0,0,0,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1,0,0,0,0,1,1,0,0],序列2为[0,0,1,1,0,0,0,1,0,0,1,0,1,0,0,0,0,1,1,0,0,0,0,1,0,1,0,0,1,0,0,0,1,1,0,0]。这样我们便需要一个有36个节点的神经网络来储存这两个图片,权重矩阵为36x36维。
更新网络权值矩阵公式为:
其中k表示需要储存的k个序列,这里k=2;![]() 表示第s个序列,
表示第s个序列,![]() 和
和![]() 表示第s个序列的第i、第j个元素,对应就是第i、j个节点,所以说序列是通过神经元输入网络的。
表示第s个序列的第i、第j个元素,对应就是第i、j个节点,所以说序列是通过神经元输入网络的。![]() 代表权值矩阵的第i行j列。所以算法实现时可以用三层循环来实现:第一层循环是依次输入各个序列,二、三层循环用来计算权重矩阵i行j列。
代表权值矩阵的第i行j列。所以算法实现时可以用三层循环来实现:第一层循环是依次输入各个序列,二、三层循环用来计算权重矩阵i行j列。
(对于上面第一行的公式,更一般的形式应该可以把2改成α,1改成β,即这里α=2,β=1是一种特殊情况,换成其它参数应该也是可以的,甚至V也可以不止是1次方,也可能是其它是数)
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
a=np.array([[0,0,1,1,0,0],
[0,0,1,1,0,0],
[1,1,1,1,1,1],
[1,1,1,1,1,1],
[0,0,1,1,0,0],
[0,0,1,1,0,0]])
b=np.array([[0,0,1,1,0,0],
[0,1,0,0,1,0],
[1,0,0,0,0,1],
[1,0,0,0,0,1],
[0,1,0,0,1,0],
[0,0,1,1,0,0]])
array_a=a.flatten() #把矩阵变成序列
array_b=b.flatten()
input_array=[array_a,array_b]
w=np.zeros((36,36)) #初始权值矩阵
for s in input_array:
w0=np.zeros((36,36))
for i in range(36):
for j in range(36):
if i==j:
w0[i,j]=0
else:
w0[i,j]=(2*s[i]-1)*(2*s[j]-1)
w+=w0
w=w*300 #为了以图片方式展示
w=Image.fromarray(w)
plt.imshow(w)
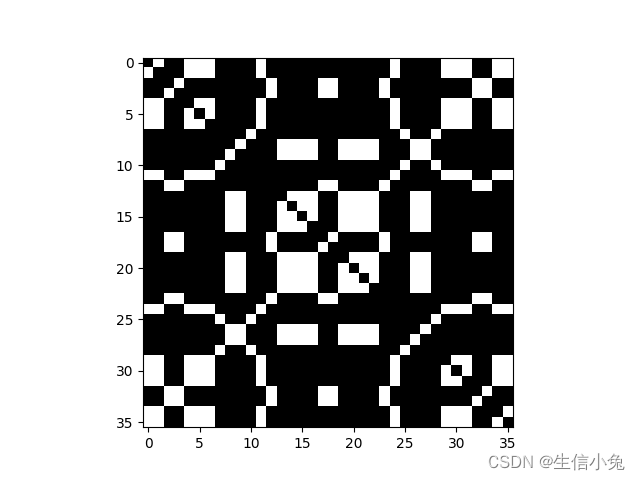
plt.show()最终我们得到了权值矩阵w,把权值矩阵按照图片方式展示,图像如下:
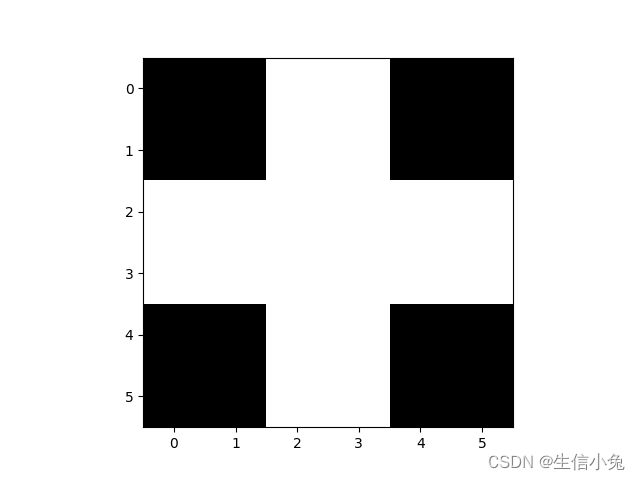
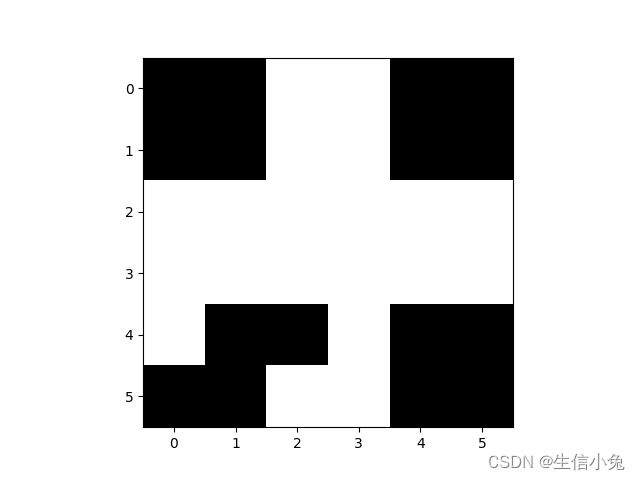
我们可以把这个权值矩阵看成是这两个输入图片的叠加后,以权值矩阵形式储存在神经网络中。那么。之后如果我们有一个新的相同维度的图片,但是有一部分模糊了,就可以利用这个神经网络还原成原来的图像。例如,对于下面这样的图像:
我们把它还原回之前的形状。我们把这个图像矩阵按行展开成序列,该序列还是用V表示,序列处理后还原成新的序列用Y表示。实现过程为:
上面两个过程是循环操作的。开始输入V初始序列,Vj表示序列第j个元素,wij表示权值矩阵第i行j列,即矩阵第j列所有元素与V中所有元素对应相乘(除了i=j这个元素不操作)并求和得Yj,如果Yj小于零,新的序列第j个元素就是0,否则是1。操作一遍后得到的V再输入到第一个式子处理,循环多次,最终结果会趋于稳定,此时得到就是还原后的序列。如果是矩阵的话,把序列再按照原来展开方式堆叠回去就可以了。
在每一次循环中,更新节点j的顺序不同,对最终结果也是有一定影响的。比如一个序列[1,0,0,0,1],我们可以按顺序更新,即j=1,然后依次是2,3,4,5,下一次循环也是1,2,3,4,5。但是也可以是:2,1,3,5,4, 2,1,3,5 ,4...... 这样顺序来更新。
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
a=np.array([[0,0,1,1,0,0],
[0,0,1,1,0,0],
[1,1,1,1,1,1],
[1,1,1,1,1,1],
[0,0,1,1,0,0],
[0,0,1,1,0,0]])
b=np.array([[0,0,1,1,0,0],
[0,1,0,0,1,0],
[1,0,0,0,0,1],
[1,0,0,0,0,1],
[0,1,0,0,1,0],
[0,0,1,1,0,0]])
c=np.array([[0,0,1,1,0,0],
[0,0,1,1,0,0],
[1,1,1,1,1,1],
[1,1,1,1,1,1],
[1,0,0,1,0,0],
[0,0,1,1,0,0]])
array_a=a.flatten()
array_b=b.flatten()
input_array=[array_a,array_b]
w=np.zeros((36,36))
for s in input_array:
w0=np.zeros((36,36))
for i in range(36):
for j in range(36):
if i==j:
w0[i,j]=0
else:
w0[i,j]=(2*s[i]-1)*(2*s[j]-1)
w+=w0
c=c.flatten()
v0=c
Y=np.zeros(36)
for t in range(10):
v1 = np.zeros(36)
for j in range(36):
for i in range(36):
if i==j:
v1[j]+=0
else:
v1[j]+=w[i,j]*v0[i]
if v1[j]<0:
Y[j]=0
else:
Y[j]=1
v0=Y
result=np.array(v0).reshape(6,6)
p=Image.fromarray(result*600)
plt.imshow(p)
plt.show()最终结果为:
我们发现最终确实还原回去了,效果比较好,但是Hopfield网络也是有一定缺点的。Hopfield缺点有:记忆容量有限,伪稳定点的联想与记忆,当记忆样本比较相近,就不能会议正确的记忆等等。
(2)TSP问题求解
针对TSP问题,其实是有非常多的算法,例如蚁群算法、遗传算法、模拟退火等一系列算法。TSP问题是不重复地走遍所有城市并返回起始城市,使得整个路径最短。对于n个城市,我们通常用nxn维距离矩阵 D来表示各个城市之间的距离。矩阵x行y列表示城市x与城市y之间的距离,即![]() ,对角线元素为0,因为距离是对称的,所以距离阵是对称阵。
,对角线元素为0,因为距离是对称的,所以距离阵是对称阵。
TSP目的是寻找最短路线,那么我们可以用神经网络的节点来表示路线。对于访问顺序,我们可以用换位矩阵 V表示。例如对于四个城市A,B,C,D,其中一种走法表示为:
| A | 1 | 0 | 0 | 0 |
| B | 0 | 0 | 1 | 0 |
| C | 0 | 1 | 0 | 0 |
| D | 0 | 0 | 0 | 1 |
| 一 | 二 | 三 | 四 |
它表示的路线是A -> C-> B -> D -> A 。并且我们发现,换位矩阵每一行和每一列只能有一个元素为1,其它为0。
对于n个城市,我们用节点个数为![]() 的网络,每个节点为
的网络,每个节点为![]() (换位矩阵的x行i列),表示第x个城市第i步,如果为0,就是第i步不在城市x;如果为1,就是在所以每个节点为0或1。
(换位矩阵的x行i列),表示第x个城市第i步,如果为0,就是第i步不在城市x;如果为1,就是在所以每个节点为0或1。
(注意:在这里一定要注意各个符号的表示意义,本文这里x、y始终表示的是城市,i、j始终表示第i、j步,![]() 表示城市x和y之间的距离,
表示城市x和y之间的距离,![]() 数值为0或1,表示第i步是否在城市x)。
数值为0或1,表示第i步是否在城市x)。
对于这样的神经网络,此时权值矩阵的固定的(这一点与上一个应用是截然不同的,前面的是往节点输入数据,通过网络权值起到保存数据的作用;这里权值矩阵与城市距离阵有关,距离阵固定下来,权值阵便固定下来了,变化的是网络是节点数值,最终网络稳定时节点的结果就是最终换位矩阵,表示求得的路线)。之后需要的就是多次迭代,改变节点的状态,找到最终的结果。
迭代过程需要引入Uxi这个中间量。U与换位矩阵V维数相同,U0这里可以为0.2。A、D是常数,这里分别为1.5、1;t用来表示第几次迭代次数,那么![]() 就可以表示第t次迭代时换位矩阵x行i列的数,
就可以表示第t次迭代时换位矩阵x行i列的数,![]() 也是如此,
也是如此,![]() 、
、![]() 表示第t次时的矩阵。
表示第t次时的矩阵。
运算步骤:
(1)初始时t=0,随机初始化矩阵![]() ,U中每个数在0附近。
,U中每个数在0附近。
(2)计算V:
(3)根据得到的V,计算![]() :
:
其中n为城市数,也就是矩阵V、U的维数。
(4)计算![]() :
:
![]() 为步长,类似于学习率,一般为0.1左右。
为步长,类似于学习率,一般为0.1左右。
(5)新的U在回到的(2)步,多次循环,重复步骤(2)![]() (4),最终的矩阵V就是结果。
(4),最终的矩阵V就是结果。
在上面步骤中,计算矩阵V、U时是按照矩阵中逐个元素计算的,即一一对应(如![]() 与
与![]() 都是矩阵的x行i列元素),最终得到这个矩阵的结果。我们注意到(3)中,当累加过程中,当i=n时,最后一项中
都是矩阵的x行i列元素),最终得到这个矩阵的结果。我们注意到(3)中,当累加过程中,当i=n时,最后一项中![]() 是不存在的,V矩阵没有第n+1列的,兔兔认为这种情况下用
是不存在的,V矩阵没有第n+1列的,兔兔认为这种情况下用![]() 就可以了。
就可以了。
关于整个循环过程中每次循环后效果如何,也就是路径是否变短,也可以用网络能量来侧面反映,因为Hopfield网络求TSP问题的思想就是由节点的状态来判断网络的能量,并且随着网络能量的降低逐渐收敛到结果,前面的所有公式也是由网络能量函数推导出来的。
根据每次循环得到的U,V代入上式即可求出此时网络的能量。关于此式最后一项![]() 超出维数的问题,和上面处理方法相同。
超出维数的问题,和上面处理方法相同。
import numpy as np
class Hopfield:
def __init__(self,city_position,circle=50,T=0.1,A=1.5,D=2):
self.city_position=city_position #城市位置坐标
self.n=len(city_position) #城市个数
self.circle=circle #循环次数
self.T=T #delta_t
self.d=self.d() #距离矩阵
self.v=self.v() #换位矩阵
self.u0=0.2
self.A=A
self.D=D
def d(self):
'''求距离阵'''
d=np.zeros((self.n,self.n))
for i in range(self.n):
for j in range(self.n):
if i==j:
d[i,j]=0
else:
d[i,j]=np.sqrt((self.city_position[i,0]-self.city_position[j,0])**2+
(self.city_position[i,1]-self.city_position[j,1])**2)
return d
def tanh(self,x):
return 2/(1+np.exp(-2*x))-1
def v(self):
'''初始化换位矩阵'''
a=np.arange(0,self.n)
np.random.shuffle(a)
v=np.zeros((self.n,self.n))
for i in range(self.n):
v[a[i],i]=1
return v
def cal_du_dt(self,v):
'''计算dU/dt'''
du_dt=np.zeros((self.n,self.n))
for x in range(self.n):
for i in range(self.n):
p1=0;p2=0;p3=0
for j in range(self.n):
p1+=v[x,j]
for y in range(self.n):
p2+=v[y,i]
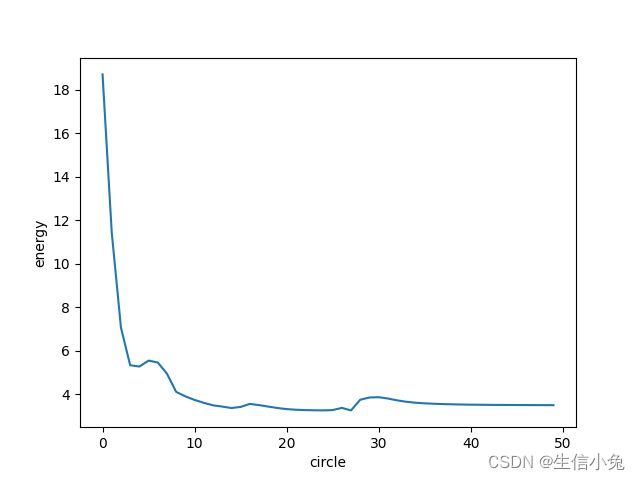
if i最终我们发现能量变化为:
我们发现能量的确是下降了,说明最终是可以收敛到比较短的路径的结果。但是结果却不是很合理,因为我们要求交换矩阵每一行每一列只能有一个元素为1,其它的为0,但是该程序运行后大部分数很小以至于接近0,其它的比较大的数认为是1,会出现某一行中有多个1,但这是不合理的,偶尔可能会得到比较合理的结果。事实上,用hopfield求解TSP问题本身效果也不是很好,一方面计算速度与其它算法相比较慢,并且会出现陷入局部解的情况,此时虽然网络能量很低,但求得的路径长度还不是比较短的路径。
总结
关于hopfield神经网络,主要用于数据储存恢复以及求解TSP问题,其中主要用途还是用于数据存储与恢复,它或许有些类似大脑存储信息的模式,也有待于深入的研究;而对于求解TSP问题,事实证明效果并不是很好,但是基于网络能量并用微分方程等数学方法以及电路的方法对网络进行分析却是值得深入研究的。本文关于两种方法仅给出了计算方法,而关于这个网络的理论基础以及这些计算公式推导方法,还是需要很大的篇幅,兔兔之后会在另外的文章中探讨。