Levenberg-Marquardt(LM算法)的理解

1. convex optimization

先简单介绍一下凸优化的内容
First quickly introduction the convex optimization concepts.

1.1 convex set

Definition:
for $x_1,x_2\in A$, we say $A$ is a convex set if and only if the following holds for any $\theta \in [0,1]$:
$$\theta x_1+(1-\theta )x_2\in A$$

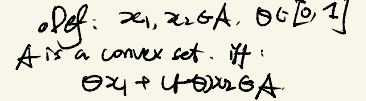
凸函数的定义如上，不过可以通过下面的图简单理解。可以直觉得说，如果两点集合内的点的“连线“上的点都在集合内，那么它就是一个凸集合。
We can quickly understand it by the following graph. If all the elements between $x_1$ and $x_2$ are in the set $A$, we could say it is a convex set.

1.2 convex function

Definition:
we say $f(x)$ with domain $dom(f)$ is a convex function, if and only if , the following conditions holds for any $\theta \in [0,1]$:
$$f(\theta x_1+(1-\theta )x_2)\le \theta f(x_1)+(1-\theta )f(x_2)$$

$$\theta x_1+(1-\theta )x_2,x_1,x_2\in dom(f)$$

1.3 optimization problem

General form:

$$minimize:f_0(x)$$

$$subjectto:f_i(x)\le 0,i\in 1,2,...,n$$

$$h_j(x)=0,j\in 1,2,...,m$$

$f_0(x)$ is the objective function, and $f_i(x)$ are inequality constraints, $h_j(x)$ are equality constraints.
$f_0(x)$是优化的目标函数， $f_i(x)$ 是不等式优化条件， $h_j(x)$ 是等式优化条件。

for examples:

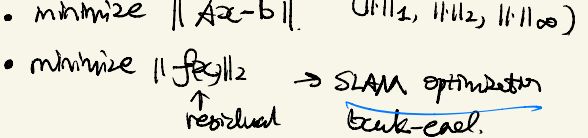
上面有几个简单的优化例子，可以发现SLAM问题（优化残差）也是其中之一。

1.4 convex optimization

$f_0(x)$ , $f_i(x)$ are all convex functions, and $h_j(x)$ are affline equations, then the problem is a convex optimization problem.
如果$f_0(x)$ ， $f_i(x)$ 都是凸函数的话，$h_j(x)$是affline， 那么问题就变成了凸优化问题。

为什么要引入凸优化问题呢？问题我们可以证明在凸优化问题中，局部最小值就是全局最小值！而且凸优化是一个成熟的技术，有非常成熟快速高效和完善的解决算法。
也就是说，如果我们证明一个问题是凸优化问题，我们就可以保证它有快速高效的精确解！

1.5 Duality

2. SLAM Bundle Adjustment

SLAM的后端Bundle Adjustment其实是一个无约束的最小二乘范数下的优化问题（但是它不一定是凸的，或许是，我也不知道有没有人去证明过，这应该是一个很好的研究课题！）。

2.1 Gauss Newton’s method

我们常用的有牛顿法，是直接对目标函数$f_0(x)$ （下图中的$F(x)$）进行处理的。

另外有高斯牛顿法，是对残差函数进行处理，我们简单写出了它的求导过程：

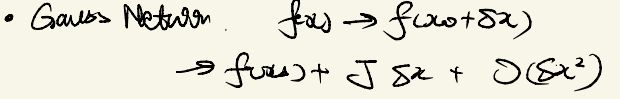
2.2 LM法

LM法则是在GN的基础上增加了一个阻尼因子。对于这个阻尼因子，不同的人有很多种解释方式（比如对x增加了一个阻尼，阻尼因子很大时接近最速下降法，阻尼因子比较小时，则更加接近高斯牛顿）。
但是我个人比较倾向于通过regularization来解读它。

2.3 Regularizaion in optimization

我们考虑这样一个问题：

在优化原本的目标函数的同时，增加了一个对x的regularization限制。对于这一个增加的regularization项，同样有很多解读方式，在这里我介绍一下其中一种：
引入regularization是由于A的误差：

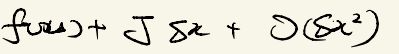
在我们的SLAM问题中，A其实是残差函数的雅各比，b则是在线性化位置的残差函数的值（$f(x_0)$）。很明显，由于在$x_0$附近进行了线性化，其实在这里是存在误差的。我们假设误差为$\Delta$的话：

这样的话，如果我们限制$\delta x$的大小，则可以限制整个线性化中引入的误差。

• 其实从泰勒展开的角度看，我们是在$x_0$附近做的泰勒展开，如果偏离$x_0$过多，那么我们的线性化近似就失效了！所以必须保证$x_0+\delta x$在$x_0$附近活动。
• 而且我们可以发现，$\mu$的选取是和$\Delta$相关的！

2.4 $\mu$的选取

$\Delta$其实是和hessian矩阵相关的。

而在GN算法中，其实是使用$J^{T}J$来近似hessian矩阵的，所以我们会在LM算法中见到$\mu$的初试化：