深度 | 一文搞懂相机标定

相机标定，是图像测量和机器视觉应用时，绕不过去的关键步骤。通过标定，可以获得相机成像几何模型的参数，也就是三维空间中点与二维图像中点的对应关系。本文通过拆解相机成像的原理、过程及相机畸变，探讨相机标定的重要性，并介绍分析了几种常见的相机标定方法。 

01 相机成像的原理

相机成像，实际上是一个光学成像过程。

我们将相机的镜头看作一个凸透镜，光线通过透镜在感光元件（CCD/CMOS）上成像，感光元件将光电信号转换为数字信号，再经数字信息处理（DSP）成数字图像，存储到存储介质当中。

​

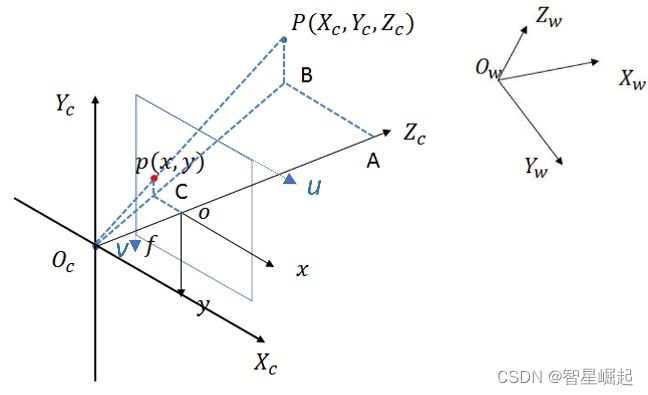
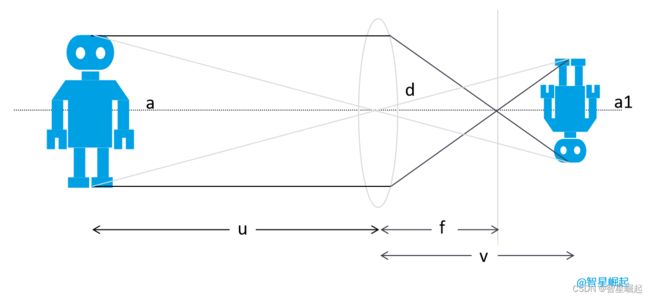透镜成像原理，凸透镜的中心为光心，光线平行于主光轴（虚线）穿过透镜时，会汇聚到焦点，然后折射成像。其中，机器人a为实物，u为物距；机器人a1为成像，v为相距；f为焦距，表示焦点到光心的距离。

 

当相机感光元件位于凸透镜焦点附近，焦距与光心到感光元件距离无限接近时，即，相机成像模型就成了我们熟悉的「小孔成像」。

小孔成像模型

在相机成像过程中，一共涉及4个坐标系：

• 世界坐标系：由用户定义的三维世界坐标系，描述物体和相机在真实世界中的位置，原点可以任意选择。

• 相机坐标系：以相机的光心为坐标原点，x轴和y轴平行于图像坐标系的x轴和y轴，z轴为相机的光轴。

• 图像坐标系：与成像平面重合，以成像平面的中心（光轴与成像平面的交点）为坐标原点，x 轴和 y轴分别平行于成像平面的两条边。

• 像素坐标系：与成像平面重合，以成像平面的左上角顶点为原点，x 轴和 y 轴分别平行于图像坐标系的x轴和y轴。

举个例子，世界坐标系下的点 ，在相机坐标系中的坐标为，投影到图像坐标系后坐标为，对应在像素坐标系中的坐标为。

为了便于计算，我们将成像平面和物体放到了同一侧：​

相机成像模型

02 用数学语言拆解相机成像

相机成像过程可以理解为坐标系间的三次变换。在理想情况下（不考虑畸变），变换过程如图：

相机成像过程

首先，世界坐标系→相机坐标系

世界坐标系到相机坐标系的转换属于刚体变换，通过旋转和平移即可获得，其中旋转矩阵为 ，平移矩阵为 。

然后，相机坐标系→图像坐标系

从相机坐标系到图像坐标系满足透视投影关系：

最后，图像坐标系→像素坐标系

像素坐标系的单位为pixel，其中  为成像平面中心点在像素坐标系下的坐标， 和  分别表示在像素坐标系下，  轴和  轴方向每个像素的物理尺寸。

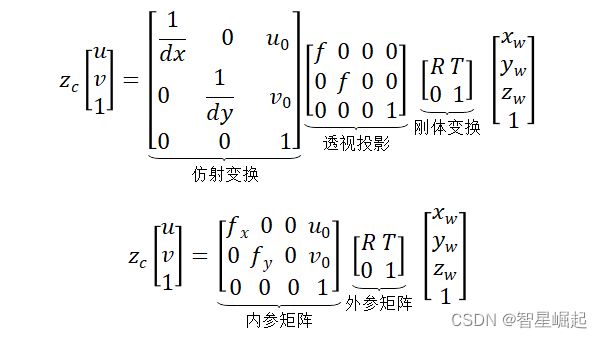
综合公式，我们就可以直接得到，从世界坐标系到像素坐标系的转换关系式：

 ​其中, 。

内参矩阵取决于相机内部参数，外参矩阵取决于相机坐标系和世界坐标系的位置。而相机标定，就可以帮我们求解出内参矩阵和外参矩阵。

 03 相机畸变又该如何矫正

大家有没有觉得，平时用手机拍出来的照片，靠边的人通常会「脸变形」？

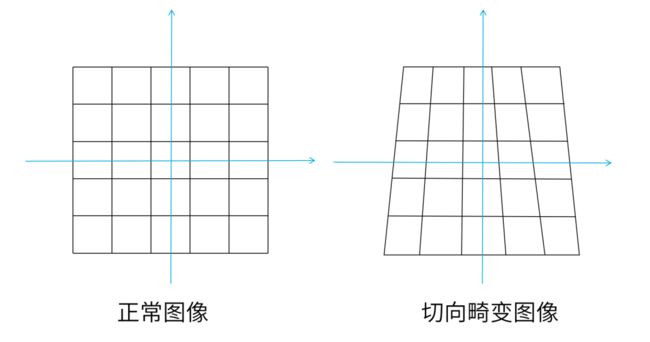
这其实是因为相机畸变。真实的镜头在成像时，会有畸变存在。由透镜形状引起的畸变是径向畸变，而由透镜安装与成像平面不平行引起的畸变是切向畸变。

径向畸变主要分为桶形畸变和枕型畸变。

​

在小孔成像模型中，一条直线投影到像素平面还是一条直线。但实际上，相机的透镜往往使真实环境中的一条直线在图片中变成了曲线，并且越靠近图像边缘越明显。由于透镜往往是中心对称的，不规则畸变也通常径向对称。

另外，如果是在相机组装过程中，透镜和感光元件CCD/CMOS的安装位置存在误差，导致透镜和成像平面没有严格平行，就会引起切向畸变。

这时，我们把一个矩形投影到成像平面，很可能就变成了一个梯形。

不过这些都问题不大，有相应的公式来进行矫正。对于径向畸变，可以用泰勒级数展开式，其中 为畸变后的实际坐标， 为矫正后坐标， 为该点距成像中心的距离：

对于切向畸变，也有矫正公式：

总的来说，相机畸变由 5个参数描述，而这些参数都可以使用相机标定来求解。质量较好的相机，切向畸变小到可忽略，径向畸变系数  也可忽略，只计算  两个参数就可以了。

​

04 常用的相机标定方法

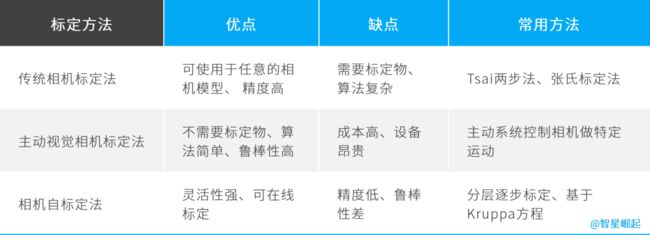
一般来说，相机标定方法有传统相机标定法、主动视觉相机标定方法、相机自标定法以及零失真相机标定法这4种。

• 传统相机标定法

需要使用尺寸已知的标定物，通过建立标定物上坐标已知的点与其图像点之间的对应，利用一定的算法获得相机模型的内外参数。

可使用于任意相机模型，精度高，但标定时始终需要标定物，必须采用两幅或两幅以上的图像，且标定物的制作精度会影响标定结果。常见的有Tsai两步法、张氏标定法等。

• 主动视觉相机标定方法

基于主动视觉的相机标定法，是指已知相机的某些运动信息对相机进行标定。通过控制相机做某些特定运动并拍摄多组图像，依据图像信息和已知位移变化来求解相机内外参数。

这种方法不需要标定物，算法简单、鲁棒性高，缺点是成本高、设备昂贵。

• 相机自标定法

自标定算法主要利用相机运动的约束，灵活性强，可对相机进行在线定标。

但它是基于绝对二次曲线或曲面的方法，算法鲁棒性差，由于相机的运动约束条件太强，在实际生活中并不实用。常见的有分层逐步标定、基于Kruppa方程等。

• 零失真相机标定法

是以LCD显示屏为参考基准，以相移光栅为媒介，建立LCD像素与相机传感器像素之间的映射关系，确定每个相机像素点在LCD上的视点位置。

​几种常见相机标定方法对比

这4种标定方法各有优劣，可以根据自己的情况来选用。其中最常用的就是的张正友标定法（张氏标定法），操作简单、精度较高，可以满足大部分场合。

张正友标定法，是利用棋盘格标定板进行标定，将世界坐标系固定在棋盘格上。棋盘格上的每个格子大小都是已知的，即棋盘格每一个角点在世界坐标系下的坐标都可以计算得到。

棋盘标定格

​

当相机拍摄标定板的图像时，通过相应的图像检测算法，就可以获得每一个角点在像素坐标系下的坐标，进而获得相机的内外参矩阵和畸变参数。需要注意的是，张正友标定法只考虑了径向畸变，没有考虑切向畸变。

以上就是本期的全部分享。至于张正友标定法如何推导等更多内容，记得持续关注「智星崛起」！