matlab 采样点数,信号频率、采样频率、频率分辨率以及FFT信号补零
采样点数,信号频率、采样频率、采样点数的区分 包含matlab代码讲解示例 清晰明了
采样点数,信号频率、采样频率、采样点数
首先,频率指的是物质在单位时间内完成周期性变化的次数叫做频率,常用f表示。【公式】:f=1/T,【物理学单位】:Hz
f -- 信号频率 fs -- 采样频率 N -- 采样点数
信号频率(f): 信号频率就是信号的频率,影响的是信号的发生函数。
采样点数(N):一次向PC端发送的数据量包含的点数,采样点数决定了每次传到PC内的数据量。
就是每个周期采了几个点。N =T/dt ;dt = 1/fs.
FFT、IFFT的采样点数必须是2的指数,在频域一个频点对应时域的一次采样,所以FFT的点数自然就是2048、1024、512、256、128.
采样率:采样率决定了采样的精度。
采样频率(Hz):波形中相邻两点间隔的实践就是采样频率(fs)的倒数。
采样频率必须大于信号的频率(不失真),fs/N(频率分辨率)越小,精度越高,通过补0增加的FFT点数无法提高FFT精度。
产生信号的总时间长度t = dt*采样数 = 采样数/fs
信号周期T = 1/f ;
产生信号的周期数 = 总时间长度/T = 总时间长度信号频率 = 采样数/采样频率信号频率
采样针对于信号处理来说的,模拟信号的数字信号处理方法就是将待处理的模拟信号经过采样、量化、编码形成数字信号,并利用数字信号处理方法对采样得到的数字信号进行处理。
频率分辨率
分辨率(resolution)是信号处理中的基本概念,它包括频率分辨率和时间分辨率。
形象地说,频率分辨率是通过一个频域的窗函数来观察频谱时所看到的频率的宽度;时间分辨率是通过一个时域的窗函数来观察信号时所看到的时间的宽度。显然,这样的窗函数越窄,相应的分辨率就越好。
频率分辨率可从两个方面来定义:
- 某个算法(如谱分析方法、功率谱估计方法等)将原信号中两个靠的很近的谱峰仍然能保持分开的能力,即物理分辨率;
- 在进行DFT时,频率轴上所能得到的最小频率间隔 ,即通常所说的计算分辨率。一般说的频率分辨率是指物理分辨率
1. DTFT和DFT的关系
首先,需要明确的是DTFT和DFT的关系。DTFT是离散时间序列的傅里叶变换,把序列映射到连续归一化频率域;
DFT(Discrete Fourier Transform)是离散时间序列的离散傅里叶变换,把序列映射成离散的频率序列。
DTFT(Discrete-time Fourier Transform)是具有物理意义的变换,DFT则是用于近似计算DTFT的工具,而FFT只是DFT的快速算法。
最终我们看到的DFT结果是由两部分合成出来的,一部分是具有物理意义的信号的DTFT结果,另一部分是分析手段(加窗,补零等)所带来的误差信号。
2. 频率分辨率的计算
物理分辨率是指两个靠的很近的频谱峰值能够分辨的能力,可用F0来表示。一般来说,在时域抽样率fs一定的情况下,信号长度T越长,即抽样点N越多,则物理分辨率越高。有这样的关系:
其中Ts是时域抽样间隔。
需要注意的是,这个是指真正实际的信号长度,抽样点数也是指这个长度上的抽样点数,而不是补零以后的长度或抽样点数。
| 也就是说物理分辨率F0只取决于时域信号的长度 |
计算分辨率是指对于一个点序列做点DFT,所得到的每两根谱线间的距离,就是F0'。
而这里的不再是实际的点数,而是计算DFT时候的点,如果经过补零的话,将是补零以后的点数。
情况一:如果采样频率为fs,采样时间间隔为ts,采样点数为N,N*ts就是采样前模拟信号的时间长度T,即采样时间为T(完成一组样本的采集所需要的时间),则频率分辨率:
Δf=fs/N=1/N*ts=1/T
所以信号长度越长,频率分辨率越好。
情况二:一段数据拿来就确定了时间T,注意:Δf=1/T,而T=N*ts,增加N必然减小ts ,因此,增加N时Δf是不变的。只有增加点数的同时导致增加了数据长度T才能使分辨率越好。
根据采样定理,数据长度T若不变,抽样点数N增加倍数与抽样频率fs增加倍数是相同的,故不能增加计算上和物理上的频率分辨力。
结论
1,频域分辨率只和采样时间长度有关,采样时间越长,频域分辨率越高;
2,时域分辨率只和采样率有关,采样率越高,时域分辨率越高。
例如,一个采样率很高,但采样时间很短的信号,其频域分辨率其实很低,但可以识别的频域范围很宽(奈奎斯特频率是采样率的二分之一)。而一个采样率很低,采样时间很长的信号,其频域分辨率很高,但能识别的带宽很低。
信号补零
频谱分辨率数值越小,频谱就越精细,分辨率越高,所以,在一个时间里,能采集的点越多越好。
特别是在采样率高的情况下,采样率作为分子,是降低分辨率的一个因素,因此高频采样中,能采集的点越多越好。
在采集点数不足时,有一个方法可以提高频谱分辨率,就是信号补零。注意,这个提高只是视觉上的提高,并没有再物理上有相应的提高。也就是没有的频率成分你补零之后还是没有
一般如果信号不是2^n的长度,会补零把信号补到2^n的长度,这样是因为2^n长度的傅里叶信号计算会更快更准。
matlab绘图
%% 信号采样
% 信号生成
f = 200; % 信号频率
Tf = 1/f; % 0.005 一个信号周期的时间
% t = (0:0.00001:20*Tf); % 信号的时间范围 ,总的传播时间
t = linspace(0,20*Tf,1000*20); % 原信号每个周期内的点数为1000个点
% Tn = t(end)/Tf % 20 信号周期数,一共重复了20次
x = cos(2*pi*f*t); % 生成的信号
% 采样
N =50; % 自定义采样点数 一个周期的采样点数
fs = f*N; % 采样频率
dt = 1/fs; % 采样间隔,采样间隔可以理解为采样信号的周期,周期 = 1/频率
% T = (0:N-1)*dt; % 定义采样的每个时间点 一个周期采样时间
T = 0:dt:t(end); % 整个信号时间范围内采样
x1 = cos(2*pi*f*T); % 对信号进行采样
subplot(311);
plot(t,x); %原始信号
title('原始信号');
ylim([-1 1]);
subplot(312);
plot(t,x,'b',T,x1,'rp'); % 采样点
title('采样过程');
ylim([-1 1]);
subplot(313)
plot(T,x1) %采样信号
title('采样后的信号')
ylim([-1 1])
xlabel('时间/s')
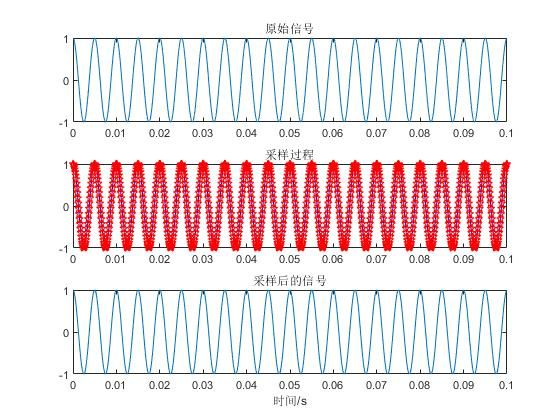
采样点数为50.jpg
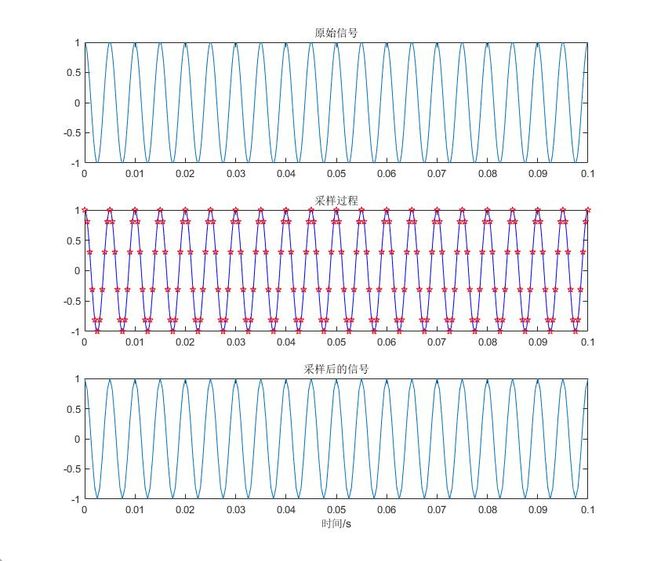
采样点数为10.jpg
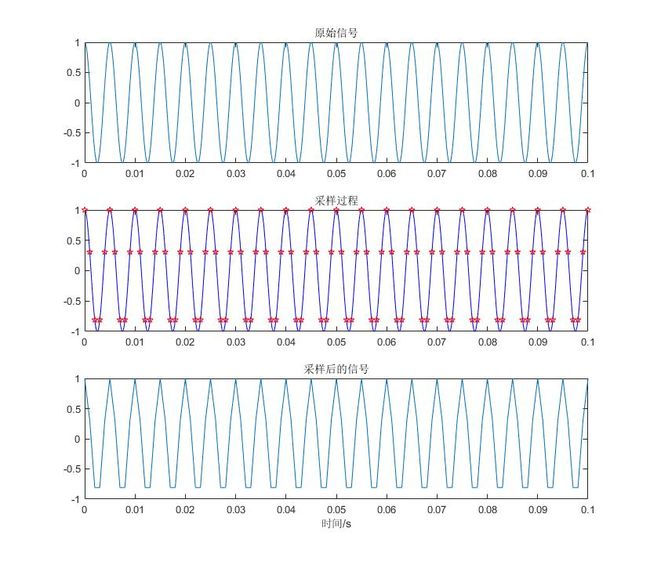
采样点数为5.jpg
从图中可以看出,采样点数越多,采样频率越大,采样后的信号与原信号越精确,否则会出现波形失真。
转载参考链接
信号频率、采样频率、采样点数 - 简书 (jianshu.com)
(18条消息) 频谱分析-FFT之后的那些事情_尘中远的程序开发记录-CSDN博客_fft之后的频谱图
采样频率、时间分辨率、频率分辨率、样本长度与采样点数之间关系_Bridgette_Yang的博客-CSDN博客_采样频率和分辨率
matlab图像频谱分析代码_频谱分析中的小插曲1——频率分辨率_weixin_39638014的博客-CSDN博客