强化学习之Policy Gradient及代码是实现
导读
强化学习的目标是学习到一个策略 π θ ( s ) \pi_{\theta}(\mathrm{s}) πθ(s)来最大化期望回报,一种直接的方法就是在策略空间直接搜出最佳的策略,称为搜索策略。策略搜索的本质是一个优化问题,可以分为基于梯度的优化和无梯度优化。策略搜索与基于价值函数的方法相比,策略搜索不需要值函数,可以直接优化策略。参数化的策略能够处理连续状态和动作,可以直接学出随机性策略。
策略梯度(Policy Gradient)是一种基于梯度的强化学习方法.假设 π θ ( a ∣ s ) \pi_{\theta}(a|\mathrm{s}) πθ(a∣s)是一个关于 的连续可微函数(神经网络),我们可以用梯度上升的方法来优化参数 使得目标函数()最大。
模型构建
我们构建是的关于 的连续可微函数为神经网络。
神经网络的输入:以向量或矩阵表示的机器Observation(state)
神经网络的输出:每个动作对应输出层的一个神经元。
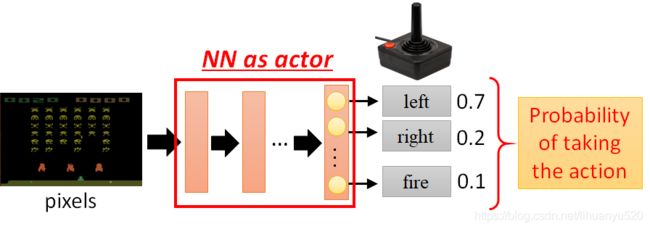
使用策略 π θ ( s ) \pi_{\theta}(\mathrm{s}) πθ(s)我们完成一次游戏,轨迹如下所示 τ = s 0 , a 0 , s 1 , r 1 , a 1 , ⋯ , s T − 1 , a T − 1 , s T , r T \tau=s_{0}, a_{0}, s_{1}, r_{1}, a_{1}, \cdots, s_{T-1}, a_{T-1}, s_{T}, r_{T} τ=s0,a0,s1,r1,a1,⋯,sT−1,aT−1,sT,rT这个轨迹的全部回报为 R θ = ∑ t = 1 T r t R_{\theta}=\sum_{t=1}^{T} r_{t} Rθ=∑t=1Trt。因为输出为每个行动的概率,所以同一个神经网络,每次 R θ R_{\theta} Rθ都是不同的。因此我们定义 R ˉ θ \bar{R}_{\theta} Rˉθ为 R θ R_{\theta} Rθ的期望, R ˉ θ \bar{R}_{\theta} Rˉθ的大小可以评价策略 π θ ( s ) \pi_{\theta}(\mathrm{s}) πθ(s)的好坏,我们希望这个期望值越大越好。
一个Episode的轨迹 τ = s 0 , a 0 , s 1 , r 1 , a 1 , ⋯ , s T − 1 , a T − 1 , s T , r T \tau=s_{0}, a_{0}, s_{1}, r_{1}, a_{1}, \cdots, s_{T-1}, a_{T-1}, s_{T}, r_{T} τ=s0,a0,s1,r1,a1,⋯,sT−1,aT−1,sT,rT则每个 τ \tau τ出现的概率 P ( τ ∣ θ ) = p ( s 1 ) p ( a 1 ∣ s 1 , θ ) p ( r 1 , s 2 ∣ s 1 , a 1 ) p ( a 2 ∣ s 2 , θ ) p ( r 2 , s 3 ∣ s 2 , a 2 ) ⋯ = p ( s 1 ) ∏ t = 1 T p ( a t ∣ s t , θ ) p ( r t , s t + 1 ∣ s t , a t ) \begin{array}{l} P(\tau \mid \theta)= p\left(s_{1}\right) p\left(a_{1} \mid s_{1}, \theta\right) p\left(r_{1}, s_{2} \mid s_{1}, a_{1}\right) p\left(a_{2} \mid s_{2}, \theta\right) p\left(r_{2}, s_{3} \mid s_{2}, a_{2}\right) \cdots \end{array}\\=p\left(s_{1}\right) \prod_{t=1}^{T} p\left(a_{t} \mid s_{t}, \theta\right) p\left(r_{t}, s_{t+1} \mid s_{t}, a_{t}\right) P(τ∣θ)=p(s1)p(a1∣s1,θ)p(r1,s2∣s1,a1)p(a2∣s2,θ)p(r2,s3∣s2,a2)⋯=p(s1)t=1∏Tp(at∣st,θ)p(rt,st+1∣st,at)
其中
因为每进行一次Episode,每一个轨迹 τ \tau τ都有可能被采样。我们将在神经网络参数 θ θ θ固定条件下,选择轨迹 τ \tau τ的概率为(|)。所以有 R ˉ θ ⋅ = ∑ τ R ( τ ) P ( τ ∣ θ ) ≈ 1 N ∑ n = 1 N R ( τ n ) \bar{R}_{\theta}^{\cdot}=\sum_{\tau} R(\tau) P(\tau \mid \theta) \approx \frac{1}{N} \sum_{n=1}^{N} R\left(\tau^{n}\right) Rˉθ⋅=τ∑R(τ)P(τ∣θ)≈N1n=1∑NR(τn)穷举所有的轨迹不可能的,这里的近似采用了蒙特卡洛采样的方法,我们使用策略 π θ ( s ) \pi_{\theta}(\mathrm{s}) πθ(s),完成 N N N次Episode,会得到 N N N个轨迹,即 { τ 1 , τ 2 , ⋯ , τ N } \left\{\tau^{1}, \tau^{2}, \cdots, \tau^{N}\right\} {τ1,τ2,⋯,τN},将将这N次得到回报取平均,当N趋向于无穷时候,两者近似。
我们的目标是最大化期望回报 θ ∗ = arg max θ R ˉ θ \theta^{*}=\arg \max _{\theta} \bar{R}_{\theta} θ∗=argθmaxRˉθ我们可以采用梯度上升的方法进行求解,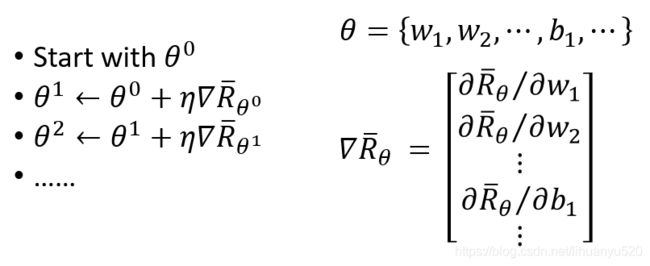 (1) 已知条件 R ˉ θ ⋅ = ∑ τ R ( τ ) P ( τ ∣ θ ) \bar{R}_{\theta}^{\cdot}=\sum_{\tau} R(\tau) P(\tau \mid \theta) Rˉθ⋅=∑τR(τ)P(τ∣θ),我们求 ∇ R ˉ θ \nabla \bar{R}_{\theta} ∇Rˉθ?
(1) 已知条件 R ˉ θ ⋅ = ∑ τ R ( τ ) P ( τ ∣ θ ) \bar{R}_{\theta}^{\cdot}=\sum_{\tau} R(\tau) P(\tau \mid \theta) Rˉθ⋅=∑τR(τ)P(τ∣θ),我们求 ∇ R ˉ θ \nabla \bar{R}_{\theta} ∇Rˉθ?
∇ R ˉ θ = ∑ τ R ( τ ) ∇ P ( τ ∣ θ ) = ∑ τ R ( τ ) P ( τ ∣ θ ) ∇ P ( τ ∣ θ ) P ( τ ∣ θ ) = ∑ τ R ( τ ) P ( τ ∣ θ ) ∇ log P ( τ ∣ θ ) ≈ 1 N ∑ n = 1 N R ( τ n ) ∇ log P ( τ n ∣ θ ) \nabla \bar{R}_{\theta}=\sum_{\tau} R(\tau) \nabla P(\tau \mid \theta)=\sum_{\tau} R(\tau) P(\tau \mid \theta) \frac{\nabla P(\tau \mid \theta)}{P(\tau \mid \theta)} \\\\ \begin{array}{l} =\sum_{\tau} R(\tau) P(\tau \mid \theta) \nabla \log P(\tau \mid \theta) \\\\ \approx \frac{1}{N} \sum_{n=1}^{N} R\left(\tau^{n}\right) \nabla \log P\left(\tau^{n} \mid \theta\right) \end{array} ∇Rˉθ=τ∑R(τ)∇P(τ∣θ)=τ∑R(τ)P(τ∣θ)P(τ∣θ)∇P(τ∣θ)=∑τR(τ)P(τ∣θ)∇logP(τ∣θ)≈N1∑n=1NR(τn)∇logP(τn∣θ)注意 dlog ( f ( x ) ) d x = 1 f ( x ) d f ( x ) d x \frac{\operatorname{dlog}(f(x))}{d x}=\frac{1}{f(x)} \frac{d f(x)}{d x} dxdlog(f(x))=f(x)1dxdf(x)。
(2)接下来我们对 ∇ log P ( τ ∣ θ ) \nabla \log P\left(\tau \mid \theta\right) ∇logP(τ∣θ)进行推导式求解?
有上文 P ( τ ∣ θ ) = p ( s 1 ) ∏ t = 1 T p ( a t ∣ s t , θ ) p ( r t , s t + 1 ∣ s t , a t ) P\left(\tau \mid \theta\right) = p\left(s_{1}\right) \prod_{t=1}^{T} p\left(a_{t} \mid s_{t}, \theta\right) p\left(r_{t}, s_{t+1} \mid s_{t}, a_{t}\right) P(τ∣θ)=p(s1)∏t=1Tp(at∣st,θ)p(rt,st+1∣st,at),所以有
log P ( τ ∣ θ ) = log p ( s 1 ) + ∑ t = 1 T log p ( a t ∣ s t , θ ) + log p ( r t , s t + 1 ∣ s t , a t ) ∇ log P ( τ ∣ θ ) = ∑ t = 1 T ∇ log p ( a t ∣ s t , θ ) \begin{array}{l} \log P(\tau \mid \theta) =\log p\left(s_{1}\right)+\sum_{t=1}^{T} \log p\left(a_{t} \mid s_{t}, \theta\right)+\log p\left(r_{t}, s_{t+1} \mid s_{t}, a_{t}\right) \\\\ \nabla \log P(\tau \mid \theta)=\sum_{t=1}^{T} \nabla \log p\left(a_{t} \mid s_{t}, \theta\right) \end{array} logP(τ∣θ)=logp(s1)+∑t=1Tlogp(at∣st,θ)+logp(rt,st+1∣st,at)∇logP(τ∣θ)=∑t=1T∇logp(at∣st,θ)
(3)我们对参数 θ θ θ进行更新,由 θ new ← θ old + η ∇ R ˉ θ old \theta^{\text {new}} \leftarrow \theta^{\text {old}}+\eta \nabla \bar{R}_{\theta^{\text {old}}} θnew←θold+η∇Rˉθold
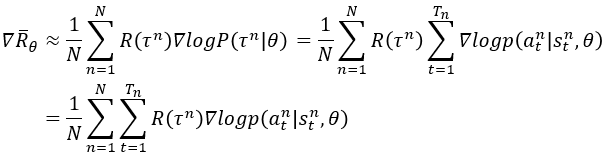
更新过程如下图所示:

总结下来就是:增加带来正激励的概率;减少带来负激励的概率,并且我们考虑的是整个轨迹的回报。
Reinforce算法
因为 R θ = ∑ t = 1 T r t R_{\theta}=\sum_{t=1}^{T} r_{t} Rθ=∑t=1Trt,所以 ∇ R ˉ θ = 1 N ∑ n = 1 N ∑ t = 1 T n ∇ log p ( a t n ∣ s t n , θ ) ( ∑ t = 1 T r t ) \nabla \bar{R}_{\theta}=\frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}} \nabla \log p\left(a_{t}^{n} \mid s_{t}^{n}, \theta\right)(\sum_{t=1}^{T} r_{t}) ∇Rˉθ=N1n=1∑Nt=1∑Tn∇logp(atn∣stn,θ)(t=1∑Trt)结合随机梯度上升算法,我们可以每次采集一条轨迹,计算每个时刻的梯度并更新参数,这称为REINFORCE算法[Williams, 1992],此时
代码实现
import argparse
import gym
import numpy as np
from itertools import count
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.distributions import Categorical
parser = argparse.ArgumentParser(description='PyTorch REINFORCE example')
parser.add_argument('--gamma', type=float, default=0.99, metavar='G',
help='discount factor (default: 0.99)')
parser.add_argument('--seed', type=int, default=543, metavar='N',
help='random seed (default: 543)')
parser.add_argument('--render', action='store_true',
help='render the environment')
parser.add_argument('--log-interval', type=int, default=10, metavar='N',
help='interval between training status logs (default: 10)')
args = parser.parse_args()
env = gym.make('CartPole-v1')
env.seed(args.seed)
torch.manual_seed(args.seed)
class Policy(nn.Module):
#[1,4]-->[1,128]-->[1,2]-->softmax
def __init__(self):
super(Policy, self).__init__()
self.affine1 = nn.Linear(4, 128)
self.dropout = nn.Dropout(p=0.6)
self.affine2 = nn.Linear(128, 2)
self.saved_log_probs = []
self.rewards = []
def forward(self, x):
x = self.affine1(x)
x = self.dropout(x)
x = F.relu(x)
action_scores = self.affine2(x)
return F.softmax(action_scores, dim=1)
policy = Policy()
optimizer = optim.Adam(policy.parameters(), lr=1e-2)
eps = np.finfo(np.float32).eps.item()
def select_action(state):
state = torch.from_numpy(state).float().unsqueeze(0) #将observation转换成tensor
probs = policy(state)
m = Categorical(probs)
action = m.sample() #按照概率进行采样
policy.saved_log_probs.append(m.log_prob(action))#m.log_prob(value)函数则是公式中的log部分
return action.item()
def finish_episode():
R = 0
policy_loss = []
returns = []
#计算的每个动作时刻收到的回报
for r in policy.rewards[::-1]:
R = r + args.gamma * R
returns.insert(0, R)
returns = torch.tensor(returns)
returns = (returns - returns.mean()) / (returns.std() + eps) #标准化
for log_prob, R in zip(policy.saved_log_probs, returns):
policy_loss.append(-log_prob * R)
optimizer.zero_grad()
policy_loss = torch.cat(policy_loss).sum()
policy_loss.backward()
optimizer.step()
del policy.rewards[:]
del policy.saved_log_probs[:]
def main():
running_reward = 10
for i_episode in count(1):
state, ep_reward = env.reset(), 0
for t in range(1, 10000): # Don't infinite loop while learning
action = select_action(state)
state, reward, done, _ = env.step(action)
if args.render:
env.render()
policy.rewards.append(reward) #记录每一步的奖励
ep_reward += reward #回报相加
if done: #如果为True,这个eposid结束
break
#平均reward奖励
running_reward = 0.05 * ep_reward + (1 - 0.05) * running_reward
finish_episode()
if i_episode % args.log_interval == 0:
print('Episode {}\tLast reward: {:.2f}\tAverage reward: {:.2f}'.format(
i_episode, ep_reward, running_reward))
if running_reward > env.spec.reward_threshold:
print("Solved! Running reward is now {} and "
"the last episode runs to {} time steps!".format(running_reward, t))
break
if __name__ == '__main__':
main()
$ python temp.py
Episode 10 Last reward: 26.00 Average reward: 16.00
Episode 20 Last reward: 16.00 Average reward: 14.85
Episode 30 Last reward: 49.00 Average reward: 20.77
Episode 40 Last reward: 45.00 Average reward: 27.37
Episode 50 Last reward: 44.00 Average reward: 30.80
Episode 60 Last reward: 111.00 Average reward: 42.69
Episode 70 Last reward: 141.00 Average reward: 70.65
Episode 80 Last reward: 138.00 Average reward: 100.27
Episode 90 Last reward: 30.00 Average reward: 86.27
Episode 100 Last reward: 114.00 Average reward: 108.18
Episode 110 Last reward: 175.00 Average reward: 156.48
Episode 120 Last reward: 141.00 Average reward: 143.86
Episode 130 Last reward: 101.00 Average reward: 132.91
Episode 140 Last reward: 19.00 Average reward: 89.99
Episode 150 Last reward: 30.00 Average reward: 63.52
Episode 160 Last reward: 27.00 Average reward: 49.30
Episode 170 Last reward: 79.00 Average reward: 47.18
Episode 180 Last reward: 77.00 Average reward: 51.38
Episode 190 Last reward: 80.00 Average reward: 63.45
Episode 200 Last reward: 55.00 Average reward: 62.21
Episode 210 Last reward: 38.00 Average reward: 57.16
Episode 220 Last reward: 50.00 Average reward: 54.56
Episode 230 Last reward: 31.00 Average reward: 53.13
Episode 240 Last reward: 115.00 Average reward: 67.47
Episode 250 Last reward: 204.00 Average reward: 137.96
Episode 260 Last reward: 195.00 Average reward: 191.86
Episode 270 Last reward: 214.00 Average reward: 218.05
Episode 280 Last reward: 500.00 Average reward: 294.96
Episode 290 Last reward: 358.00 Average reward: 350.75
Episode 300 Last reward: 327.00 Average reward: 319.03
Episode 310 Last reward: 93.00 Average reward: 260.24
Episode 320 Last reward: 500.00 Average reward: 258.35
Episode 330 Last reward: 83.00 Average reward: 290.17
Episode 340 Last reward: 201.00 Average reward: 259.37
Episode 350 Last reward: 482.00 Average reward: 270.48
Episode 360 Last reward: 500.00 Average reward: 337.46
Episode 370 Last reward: 91.00 Average reward: 375.76
Episode 380 Last reward: 500.00 Average reward: 402.21
Episode 390 Last reward: 260.00 Average reward: 377.44
Episode 400 Last reward: 242.00 Average reward: 327.93
Episode 410 Last reward: 500.00 Average reward: 318.99
Episode 420 Last reward: 390.00 Average reward: 339.36
Episode 430 Last reward: 476.00 Average reward: 364.77
Episode 440 Last reward: 500.00 Average reward: 368.53
Episode 450 Last reward: 82.00 Average reward: 370.17
Episode 460 Last reward: 500.00 Average reward: 404.95
Episode 470 Last reward: 500.00 Average reward: 443.09
Episode 480 Last reward: 500.00 Average reward: 465.92
Solved! Running reward is now 476.20365101578085 and the last episode runs to 500 time steps!
参考
李宏毅强化学习
邱锡鹏《神经网络与深度学习》
