寿险精算实验一——编制生命表换算表
寿险精算实验一——编制生命表换算表
- 一、生命表介绍
- 二、编制换算表
-
- 2.1基本概念
- 2.2基本公式
- 2.3编制换算函数表
- 三、可视化
- 参考
一、生命表介绍
1997年4月1日我国颁布了第一张中国寿险业生命表,即中国人寿保险业经验生命表(1990一1993),差不多10年后,2006年1月1日,《中国人寿保险业经验生命表(2000一2003)》开始施行,简称: C L ( 2000 一 2003 ) CL(2000一2003) CL(2000一2003),再次经过10年,中国保监会开始颁布第三版中国人身保险业经验生命表,命名为《中国人身保险业经验生命表(2010-2013)》,英文名称为“China Life Insurance Mortality Table(2010-2013)”,简称: C L ( 2010 一 2013 ) CL(2010一2013) CL(2010一2013),其中:非养老类业务一表两张,非养老类业务二表两张,养老类业务表两张,分别是:
1.CL1(2010-2013):非养老类业务一表(男);
2.CL2(2010-2013):非养老类业务一表(女);
3.CL3(2010-2013):非养老类业务二表(男);
4.CL4(2010-2013):非养老类业务二表(女);
5.CL5(2010-2013):养老类业务表(男);
6.CL6(2010-2013):养老类业务表(女)。
根据《中国保监会关于使用《中国人身保险业经验生命表(2010-2013)》有关事项的通知》,保险公司选择适用的生命表时,应按照审慎性原则整体考虑同一产品或产品组合的全部保单:(一)定期寿险、终身寿险、健康保险应采用非养老类业务一表。(二)保险期间内(不含满期)没有生存金给付责任的两全保险或含有生存金给付责任但生存责任较低的两全保险、长寿风险较低的年金保险应采用非养老类业务二表。(三)保险期间内(不含满期)含有生存金给付责任且生存责任较高的两全保险、长寿风险较高的年金保险应采用养老类业务表。
(四)保险公司应根据产品特征综合分析,按照精算原理和审慎性原则判断生存责任和长寿风险的高低。新生命表政策将于2017年1月1日起实施。
二、编制换算表
2.1基本概念
换算表将一些计算寿险的保险费、现金价值和准备金时有规律的数值预先编制换算表,从而简化计算,提高效率。换算表有连续换算表和离散换算表,通常包含下述七项:
① x x x表示年龄;
② D x D_x Dx表示 x x x岁的生存人数与 x x x年贴现因子数值的乘积;
③ N x N_x Nx表示从 D x D_x Dx开始,并将以后各年直到 D w ( 终 极 数 ) D_w(终极数) Dw(终极数)的数值加总,其中 w w w为极限年龄;
④ C x C_x Cx表示 x x x岁的死亡人数与 x + 1 x+1 x+1年贴现因子数值的乘积;
⑤ M x M_x Mx表示从 C x C_x Cx开始直到 C w ( 终 极 数 ) C_w(终极数) Cw(终极数)的数值加总之和;
⑥ R x R_x Rx表示从 M x M_x Mx开始直到 M w ( 终 极 数 ) M_w(终极数) Mw(终极数)的数值加总之和;
⑦ S x S_x Sx表示从 N x N_x Nx开始直到 N w ( 终 极 数 ) N_w(终极数) Nw(终极数)的数值加总之和;
其中, C x , M x , R x , D x , N x , S x C_x,M_x,R_x,D_x,N_x,S_x Cx,Mx,Rx,Dx,Nx,Sx称为换算符号或换算函数。
由 C x , M x , R x C_x,M_x,R_x Cx,Mx,Rx和年龄 x x x或 D x , N x , S x D_x,N_x,S_x Dx,Nx,Sx和年龄 x x x组成的列阵称为换算函数表,简称换算表。
如果假设死亡在一年中是均匀分布的,连续模型可以用离散模型近似,即定义 C x = v x + 1 2 d x C_x=v^{x+\frac{1}{2}}d_x Cx=vx+21dx
2.2基本公式
D x = v x l x , C x = v x + 1 2 d x D_x=v^{x}l_x,C_x=v^{x+\frac{1}{2}}d_x Dx=vxlx,Cx=vx+21dx
M x = ∑ k = 0 w − x C x + k , N x = ∑ k = 0 w − x D x + k M_x=\sum_{k=0}^{w-x} C_{x+k},N_x=\sum_{k=0}^{w-x} D_{x+k} Mx=k=0∑w−xCx+k,Nx=k=0∑w−xDx+k
R x = ∑ k = 0 w − x M x + k , S x = ∑ k = 0 w − x N x + k R_x=\sum_{k=0}^{w-x} M_{x+k},S_x=\sum_{k=0}^{w-x} N_{x+k} Rx=k=0∑w−xMx+k,Sx=k=0∑w−xNx+k
2.3编制换算函数表
如果生命表和换算公式已知,且给定利率,那么就可以计算换算表了。
下面将以非养老类业务一表为例结合Python来进行实战——编制生命表换算表。
(1)Python环境准备
import pandas as pd
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', None)
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
(2)数据导入
data = pd.read_excel('LifeTable.xlsx',sheet_name=0) # 第0个表是非养老类业务一表,第1个表是非养老类业务二表,第2个表是养老类业务表
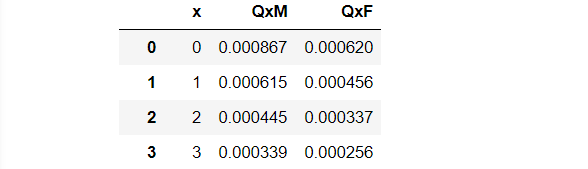
data
其中 Q x M QxM QxM表示男性死亡率, Q x F QxF QxF表示女性死亡率
部分数据如下所示:
(3)计算中间变量
接下来计算中间变量:生存概率 p x p_x px、生存人数 l x l_x lx、死亡人数 d x d_x dx和平均余命 e ˚ x \mathring e_x e˚x。
假设初始人口为10万 l 0 = 100000 l_0=100000 l0=100000,那么有:
p x = 1 − q x , l x = l x − 1 ⋅ p x − 1 , d x = l x − l x + 1 , e ˚ x = ∑ i = x + 1 w l i l x + 0.5 p_x=1-q_x,l_x=l_{x-1} \cdot p_{x-1},d_x=l_{x}-l_{x+1},\mathring e_x=\frac{\sum_{i=x+1}^{w} l_i}{l_x} +0.5 px=1−qx,lx=lx−1⋅px−1,dx=lx−lx+1,e˚x=lx∑i=x+1wli+0.5
i = 0.025 # 定价利率
v = 1 / (1+i)
w = data['QxM'].count() -1 # 极限年龄
data['PxM'] = 1- data['QxM'] # 计算生存概率
data['PxF'] = 1- data['QxF']
############# 计算中间变量
data['lxM'] = None
data['lxF'] = None
data['dxM'] = None
data['dxF'] = None
data['exM'] = None
data['exF'] = None
## 计算生存人数
for k in range(w+1):
if k == 0:
data['lxM'][0] = 100000
data['lxF'][0] = 100000
else:
data['lxM'][k] = data['lxM'][k-1] * data['PxM'][k-1]
data['lxF'][k] = data['lxF'][k-1] * data['PxF'][k-1]
## 计算死亡人数
for k in range(w+1):
if k < w:
data['dxM'][k] = data['lxM'][k] - data['lxM'][k+1]
data['dxF'][k] = data['lxF'][k] - data['lxF'][k+1]
else:
data['dxM'][k] = data['lxM'][k]
data['dxF'][k] = data['lxF'][k]
# 计算平均余命
for k in range(w+1):
if k < w:
exM =0
exF =0
for t in range(k+1,w+1):
exM = exM + data['lxM'][t]
exF = exF + data['lxF'][t]
data['exM'][k] = exM / data['lxM'][k] + 0.5
data['exF'][k] = exF / data['lxF'][k] + 0.5
else:
data['exM'][k] = 0.5
data['exF'][k] = 0.5
部分数据如下所示:

(4)计算换算表其余变量
假设利率 i = 2.5 i=2.5% i=2.5,那么:
D x = v x l x = ( 1 + i ) − x l x , C x = v x + 1 2 d x = ( 1 + i ) − ( x + 1 2 ) d x D_x=v^{x}l_x=(1+i)^{-x}l_x,C_x=v^{x+\frac{1}{2}}d_x=(1+i)^{-(x+\frac{1}{2})}d_x Dx=vxlx=(1+i)−xlx,Cx=vx+21dx=(1+i)−(x+21)dx
另外, M x , N x , R x , S x M_x,N_x,R_x,S_x Mx,Nx,Rx,Sx都可以根据公式加总得到。
data['DxM'] = (v ** data['x']) * data['lxM'] # 计算Dx
data['DxF'] = (v ** data['x']) * data['lxF']
data['CxM'] = (v ** (data['x']+0.5)) * data['dxM'] # 计算Cx
data['CxF'] = (v ** (data['x']+0.5)) * data['dxF']
# 计算Mx
data['MxM'] = None
data['MxF'] = None
for k in range(w+1):
mxM=0
mxF=0
for t in range(k,w+1):
mxM = mxM + data['CxM'][t]
mxF = mxF + data['CxF'][t]
data['MxM'][k] = mxM
data['MxF'][k] = mxF
# 计算Nx
data['NxM'] = None
data['NxF'] = None
for k in range(w+1):
nxM=0
nxF=0
for t in range(k,w+1):
nxM = nxM + data['DxM'][t]
nxF = nxF + data['DxF'][t]
data['NxM'][k] = nxM
data['NxF'][k] = nxF
# 计算Rx
data['RxM'] = None
data['RxF'] = None
for k in range(w+1):
rxM=0
rxF=0
for t in range(k,w+1):
rxM = rxM + data['MxM'][t]
rxF = rxF + data['MxF'][t]
data['RxM'][k] = rxM
data['RxF'][k] = rxF
# 计算Sx
data['SxM'] = None
data['SxF'] = None
for k in range(w+1):
sxM=0
sxF=0
for t in range(k,w+1):
sxM = sxM + data['NxM'][t]
sxF = sxF + data['NxF'][t]
data['SxM'][k] = sxM
data['SxF'][k] = sxF
data
三、可视化
下面将对新生命表死亡率进行可视化展示:
(1)Python环境与数据准备
import matplotlib.pyplot as plt
dt = pd.read_excel('LifeTable.xlsx',sheet_name=3)
dt
# 1.CL1(2010-2013):非养老类业务一表(男);
# 2.CL2(2010-2013):非养老类业务一表(女);
# 3.CL3(2010-2013):非养老类业务二表(男);
# 4.CL4(2010-2013):非养老类业务二表(女);
# 5.CL5(2010-2013):养老类业务表(男);
# 6.CL6(2010-2013):养老类业务表(女)。
(2)绘制散点图
plt.figure(figsize=(10,5))
plt.plot(dt['x'],dt['CL1'],color='red',linewidth=2.0,linestyle='--')
plt.plot(dt['x'],dt['CL2'],color='blue',linewidth=2.0,linestyle='--')
plt.plot(dt['x'],dt['CL3'],color='green',linewidth=2.0,linestyle=':')
plt.plot(dt['x'],dt['CL4'],color='gray',linewidth=2.0,linestyle=':')
plt.plot(dt['x'],dt['CL5'],color='gold',linewidth=2.0,linestyle='-.')
plt.plot(dt['x'],dt['CL6'],color='orange',linewidth=2.0,linestyle='-.')
plt.legend()
plt.show()

整体来看,由上图可知,死亡率随着年龄的增加而提高,60岁之前,死亡率变化基本不大,基本在“年龄”轴附近,随后逐渐升高,并且在105岁有个人为的截断,死亡率都变为1。
plt.figure(figsize=(10,10))
plt.plot(dt['x'][0:20],dt['CL1'][0:20],color='red',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][0:20],dt['CL2'][0:20],color='blue',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][0:20],dt['CL3'][0:20],color='darkturquoise',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][0:20],dt['CL4'][0:20],color='darkgreen',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][0:20],dt['CL5'][0:20],color='deeppink',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][0:20],dt['CL6'][0:20],color='orange',linewidth=2.0,linestyle='--')
plt.legend()
plt.show()

此外,由上图可知,5-6岁有死亡率拐点,,在此拐点之前,死亡率逐渐下降,随后又开始上升,这是因为婴幼儿不仅对疾病抵抗力较差,而且对于各种意外事故的应对和保护能力不足,导致死亡率相对较高。
plt.figure(figsize=(10,10))
plt.plot(dt['x'][20:50],dt['CL1'][20:50],color='red',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][20:50],dt['CL2'][20:50],color='blue',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][20:50],dt['CL3'][20:50],color='darkturquoise',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][20:50],dt['CL4'][20:50],color='darkgreen',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][20:50],dt['CL5'][20:50],color='deeppink',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][20:50],dt['CL6'][20:50],color='orange',linewidth=2.0,linestyle='--')
plt.legend()
plt.show()
plt.figure(figsize=(10,10))
plt.plot(dt['x'][50:80],dt['CL1'][50:80],color='red',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][50:80],dt['CL2'][50:80],color='blue',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][50:80],dt['CL3'][50:80],color='darkturquoise',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][50:80],dt['CL4'][50:80],color='darkgreen',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][50:80],dt['CL5'][50:80],color='deeppink',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][50:80],dt['CL6'][50:80],color='orange',linewidth=2.0,linestyle='--')
plt.legend()
plt.show()
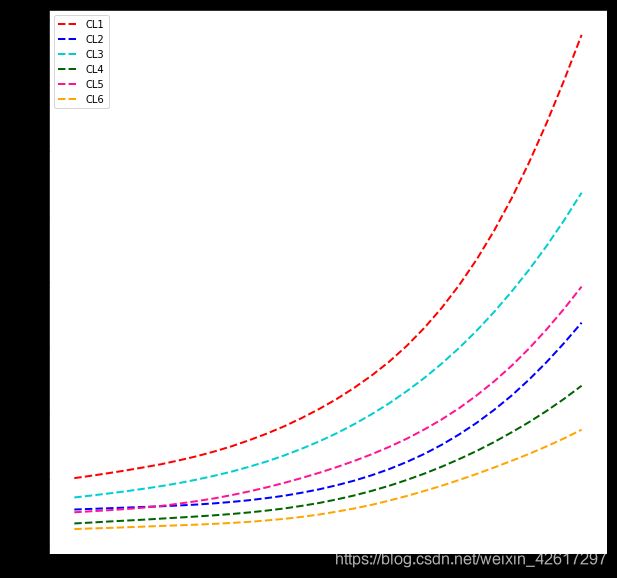
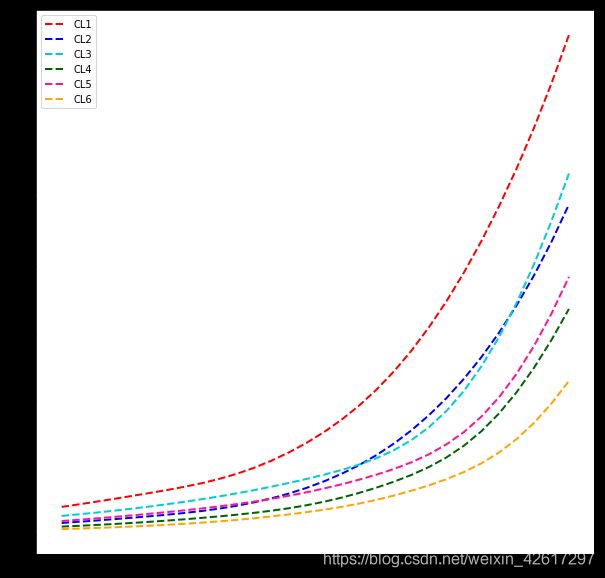
由上两张图可知,在20-70岁区间,CL2的变化趋势值得关注,可能是该时期女性面临生育、女性特有癌症等风险因素,导致死亡率偏高,但还是低于CL1的死亡率,男同胞们更要关心爱护自己的身体健康呀,烟少抽,酒少喝。。。
plt.figure(figsize=(10,10))
plt.plot(dt['x'][80:105],dt['CL1'][80:105],color='red',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][80:105],dt['CL2'][80:105],color='blue',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][80:105],dt['CL3'][80:105],color='darkturquoise',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][80:105],dt['CL4'][80:105],color='darkgreen',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][80:105],dt['CL5'][80:105],color='deeppink',linewidth=2.0,linestyle='--')
plt.plot(dt['x'][80:105],dt['CL6'][80:105],color='orange',linewidth=2.0,linestyle='--')
plt.legend()
plt.show()
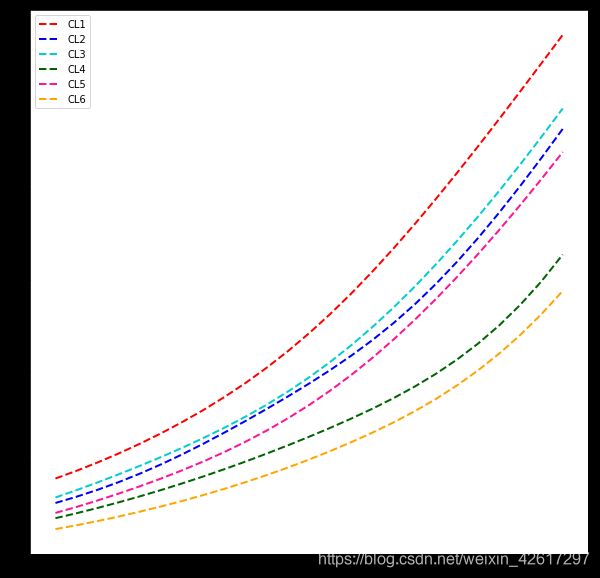
根据上图,80-104岁区间内,各个群体的死亡率基本上是上升的,基本上是 C L 1 > C L 3 > C L 2 > C L 5 > C L 4 > C L 6 CL_1>CL_3>CL_2>CL_5>CL_4>CL_6 CL1>CL3>CL2>CL5>CL4>CL6,并且死亡率都比较高,可能是因为人随着年龄的增长,健康状况越来越不乐观,各种慢性疾病发病率增高,治疗难度越来越大,导致死亡率随着年龄的增长越来越高。
参考
[1] 李秀芳 编著:寿险精算实务实验教程[M],中国财政经济出版社2008年版
