数字信号处理第三次试验：用FFT对信号作频谱分析

前言

为了帮助同学们完成痛苦的实验课程设计，本作者将其作出的实验结果及代码贴至CSDN中，供同学们学习参考。如有不足或描述不完善之处，敬请各位指出，欢迎各位的斧正！

一、实验目的

学习用FFT对连续信号和时域离散信号进行谱分析的方法，了解可能出现的分析误差及其原因，以便正确应用FFT。

二、实验原理与方法

用FFT对信号作频谱分析是学习数字信号处理的重要内容。经常需要进行谱分析的信号是模拟信号和时域离散信号。对信号进行谱分析的重要问题是频谱分辨率D和分析误差。频谱分辨率直接和FFT的变换区间N有关，因为FFT能够实现的频率分辨率是2π/N，因此要求2π/N≤N。可以根据此式选择FFT的变换区间 N。误差主要来自于用FFT作频谱分析时，得到的是离散谱，而信号（周期信号除外）是连续谱，只有当 N 较大时离散谱的包络才能逼近于连续谱，因此 N 要适当选择大一些。
周期信号的频谱是离散谱，只有用整数倍周期的长度作FFT，得到的离散谱才能代表周期信号的频谱。如果不知道信号周期，可以尽量选择信号的观察时间长一些。
对模拟信号进行谱分析时，首先要按照采样定理将其变成时域离散信号。如果是模拟周期信号，也应该选取整数倍周期的长度，经过采样后形成周期序列，按照周期序列的谱分析进行。

三、实验环境

Matlab 7.0及Matlab 2018b

四、实验内容及步骤

（1）对以下序列进行谱分析。



选择FFT的变换区间N为8和16两种情况进行频谱分析。分别打印其幅频特性曲线。并进行对比、分析和讨论。
（2）对以下周期序列进行谱分析。


选择FFT的变换区间N为8和16两种情况分别对以上序列进行频谱分析。分别打印其幅频特性曲线。并进行对比、分析和讨论。
（3）对模拟周期信号进行谱分析

选择采样频率$F_s=64Hz$，变换区间N=16,32,64三种情况进行谱分析。分别打印其幅频特性，并进行分析和讨论。

五、实验结果截图（含分析）

实验程序清单

%实验3程序exp3.m
%用FFT对信号作频谱分析
clear;close all
%===实验内容(1)===
x1n=ones(1,4);%产生序列向量x1(n)=R4(n)
M=8;xa=1:(M/2);xb=(M/2):-1:1;x2n=[xa,xb];%产生长度为8的三角波序列x2(m)
x3n=[xb,xa];
X1k8=fft(x1n,8);%计算x1n的8点DFT
X1k16=fft(x1n,16);%计算x1n的16点DFT
X2k8=fft(x2n,8);%计算x2n的8点DFT
X2k16=fft(x2n,16);%计算x2n的16点DFT
X3k8=fft(x3n,8);%计算x3n的8点DFT
X3k16=fft(x3n,16);%计算x3n的16点DFT
%以下绘制幅频特性曲线
subplot(2,2,1);mstem(X1k8);%绘制8点DFT的幅频特性图
title('(1a)8点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度');
axis([0,2,0,1.2*max(abs(X1k8))])
subplot(2,2,3);mstem(X1k16);%绘制16点DFT的幅频特性图
title('(1b)16点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度');
axis([0,2,0,1.2*max(abs(X1k16))])
figure(2)
subplot(2,2,1);mstem(X2k8);%绘制8点DFT的幅频特性图
title('(2a)8点DFT[x_2(n)]');xlabel('ω/π');ylabel('幅度');
axis([0,2,0,1.2*max(abs(X2k8))])
subplot(2,2,2);mstem(X2k16);%绘制16点DFT的幅频特性图
title('(2b)16点DFT[x_2(n)]');xlabel('ω/π');ylabel('幅度');
axis([0,2,0,1.2*max(abs(X2k16))])
subplot(2,2,3);mstem(X3k8);%绘制8点DFT的幅频特性图
title('(3a)8点DFT[x_3(n)]');xlabel('ω/π');ylabel('幅度');
axis([0,2,0,1.2*max(abs(X3k8))])
subplot(2,2,4);mstem(X3k16);%绘制16点DFT的幅频特性图
title('(3b)16点DFT[x_3(n)]');xlabel('ω/π');ylabel('幅度');
axis([0,2,0,1.2*max(abs(X3k16))])
%实验内容(2)周期序列谱分析=================
N=8;n=0:N-1;%FFT的变换区间N=8
x4n=cos(pi*n/4);
x5n=cos(pi*n/4)+cos(pi*n/8);
X4k8=fft(x4n);%计算x4n的8点DFT
X5k8=fft(x5n);%计算x5n的8点DFT
N=16;n=0:N-1;%FFT的变换区间N=16
x4n=cos(pi*n/4);
x5n=cos(pi*n/4)+cos(pi*n/8);
X4k16=fft(x4n);%计算x4n的16点DFT
X5k16=fft(x5n);%计算x5n的16点DFT
figure(3)
subplot(2,2,1);mstem(X4k8);%绘制8点DFT的幅频特性图
title('(4a)8点DFT[x_4(n)]');xlabel('ω/π');ylabel('幅度');
axis([0,2,0,1.2*max(abs(X4k8))])
subplot(2,2,3);mstem(X4k16);%绘制16点DFT的幅频特性图
title('(4b)16点DFT[x_4(n)]');xlabel('ω/π');ylabel('幅度');
axis([0,2,0,1.2*max(abs(X4k16))])
subplot(2,2,2);mstem(X5k8);%绘制8点DFT的幅频特性图
title('(5a)8点DFT[x_5(n)]');xlabel('ω/π');ylabel('幅度');
axis([0,2,0,1.2*max(abs(X5k8))])
subplot(2,2,4);mstem(X5k16);%绘制16点DFT的幅频特性图
title('(5b)16点DFT[x_5(m)]');xlabel('ω/π');ylabel('幅度');
axis([0,2,0,1.2*max(abs(X5k16))])
%实验内容(3)模拟周期信号谱分析==========
figure(4)
Fs=64;T=1/Fs;
N=16;n=0:N-1;%FFT的变换区间N=16
x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T);%对x6(t)16点采样
X6k16=fft(x6nT);%计算x6nT的16点DFT
X6k16=fftshift(X6k16);%将零频率移到频谱中心
Tp=N*T;F=1/Tp;%频率分辨率F
k=-N/2:N/2-1;fk=k*F;%产生16点DFT对应的采样点频率(以零频率为中心)
subplot(3,1,1);stem(fk,abs(X6k16),'.');box on%绘制8点DFT的幅频特性图
title('(6a)16 点|DFT[x_6(nT)]|');xlabel('f(Hz)');ylabel('幅度');
axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k16))])
N=32;n=0:N-1;%FFT的变换区间N=16
x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T);%对x6(t)32点采样
X6k32=fft(x6nT);%计算x6nT的32点DFT
X6k32=fftshift(X6k32);%将零频率移到频谱中心
Tp=N*T;F=1/Tp;%频率分辨率F
k=-N/2:N/2-1;fk=k*F;%产生16点DFT对应的采样点频率(以零频率为中心)
subplot(3,1,2);stem(fk,abs(X6k32),'.');box on %绘制8点DFT的幅频特性图
title('(6b)32点|DFT[x_6(nT)]|');xlabel('f(Hz)');ylabel('幅度');
axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k32))])
N=64;n=0:N-1;%FFT的变换区间N=16
x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T);%对x6(t)64点采样
X6k64=fft(x6nT);%计算x6nT的64点DFT
X6k64=fftshift(X6k64);%将零频率移到频谱中心
Tp=N*T;F=1/Tp;%频率分辨率F
k=-N/2:N/2-1;fk=k*F;%产生16点DFT对应的采样点频率(以零频率为中心)
subplot(3,1,3);stem(fk,abs(X6k64),'.');box on%绘制8点DFT的幅频特性图
title('(6a)64点|DFT[x_6(nT)]|');xlabel('f(Hz)');ylabel('幅度');
axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k64))])

function mstem(Xk)
M=length(Xk);
k=0:M-1;
wk=2*k/M;
stem(wk,abs(Xk),'.');
box on;%绘制M点DFT的幅频特性图
xlabel('ω/π');
ylabel('幅度');
axis([0,2,0,1.2*max(abs(Xk))]);

实验程序运行结果及分析讨论




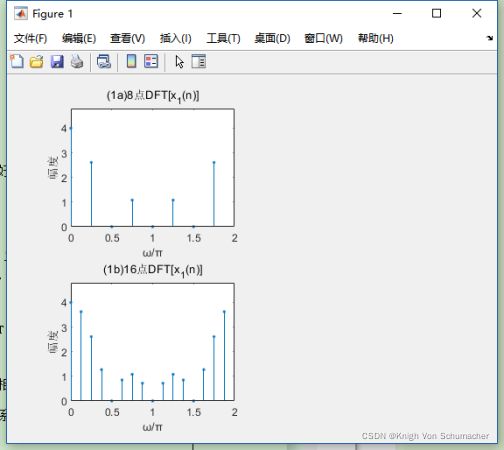
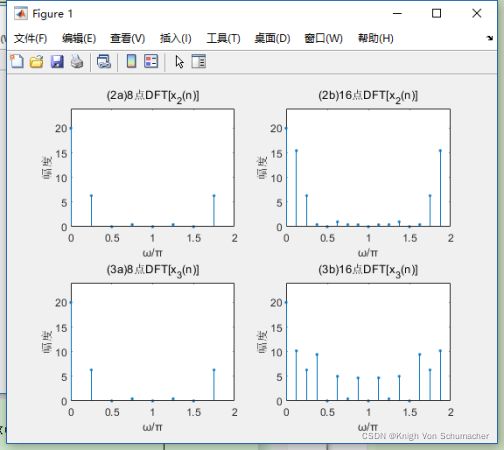
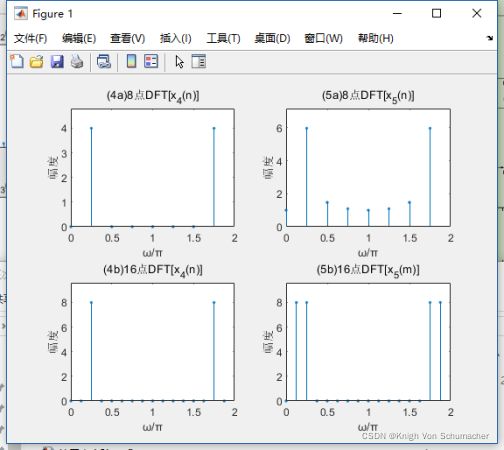
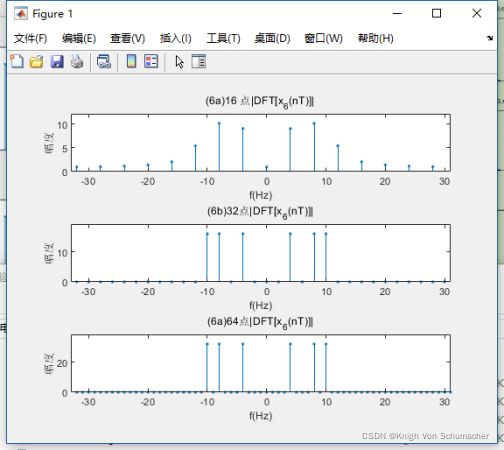
用DFT（或FFT）分析频谱，绘制频谱图时，最好将X(k)的自变量k换算成对应的频率，作为横坐标便于观察频谱。
${\omega }_k=\frac{2\pi }{N}k,k=0,1,2,\cdots ,N-1$
为了便于读取频率值，最好关于π归一化，即以$\frac{\omega }{\pi }$作为横坐标。
1、实验内容（1）
图（1a）和（1b）说明$x_1(n)=R_4(n)$的8点DFT和16点DFT分别是$x_1(n)$的频谱
函数的8点和16点采样：
因为$x_3(n)=x_2(n+3{)}_8{R}_8(n)$的8点DFT的模相等，如图（2a）和（3a）。但是，当 N=16 时，$x_3(n)$与$x_2(n)$不满足循环移位关系，所以图（2b）和（3b）的模不同。
2、实验内容（2），对周期序列谱分析
$x_4(n)=cos\frac{\pi }{4}n$的周期为8，所以N=8和N=16均是其周期的整数倍，得到正确的单一频率正弦波的频谱，仅在0.25π处有1根单一谱线。如图（4b）和（4b）所示。
$x_5(n)=cos\frac{\pi }{4}n+cos\frac{\pi }{8}n$的周期为16，所以N=8不是其周期的整数倍，得到的频谱不正确，如图（5a）所示。N=16 是其一个周期，得到正确的频谱，仅在0.25π和0.125π处有2根单一谱线, 如图（5b）所示。
3、实验内容（3），对模拟周期信号谱分析
$$x_6(n)=cos8\pi t+cos16\pi t+cos20\pi t$$
$x_6(t)$有 3 个频率成分，$f_1=4Hz,f_2=8Hz,f_3=10Hz$。所以$x_6(t)$的周期为0.5s。采样频率$F_s=64Hz=16f_1=8f_2=6.4f_3$。变换区间N=16时，观察时间$T_p=16T=0.25s$，不是$x_6(t)$的整数倍周期，所以所得频谱不正确，如图（6a）所示。变换区间N=32,64时，观察时间Tp=0.5s，1s，是$x_6(t)$的整数周期，所以所得频谱正确，如图（6b）和（6c）所示。图中3根谱线正好位于4Hz,8Hz,10Hz处。变换区间N=64时频谱幅度是变换区间N=32时2倍，这种结果正好验证了用DFT对中期序列谱分析的理论。
注意：
（1）用DFT（或FFT）对模拟信号分析频谱时，最好将X(k)的自变量 k 换算成对应的模拟频率fk，作为横坐标绘图，便于观察频谱。这样，不管变换区间N取信号周期的几倍，画出的频谱图中有效离散谐波谱线所在的频率值不变，如图（6b）和（6c）所示。
$$f_k=\frac{F_s}{N}k=\frac{1}{NT}k=\frac{1}{T_p}k,k=0,1,2,\cdots ,N-1$$
（2）本程序直接画出采样序列N点DFT的模值，实际上分析频谱时最好画出归一化幅度谱，这样就避免了幅度值随变换区间N变化的缺点。本实验程序这样绘图只要是为了验证了用DFT对中期序列谱分析的理论。

六、思考题

（1）对于周期序列，如果周期不知道，如何用FFT进行谱分析？
（2）如何选择FFT的变换区间？（包括非周期信号和周期信号）
（3）当N=8时，$x_2(n)$和$x_3(n)$的幅频特性会相同吗？为什么？N=16呢？
答：（1）如果$x(n)$的周期预先不知道，可截取M点进行DFT，即

再将截取长度扩大1倍，截取

比较$x_M(k)$和$x_{2}M(k)$，如果两者的主谱差别满足分析误差需求，则以$x_M(k)$或$x_{2}M(k)$近似表示$x(n)$，否则，继续将截取长度加倍，直至前后两次分析所得主谱频率差别满足误差要求。设最后截取长度为iM，则$X_{iM}(k_0)$表示$\omega =\frac{2\pi }{iM}{k}_0$点的谱线强度。
（2）频谱分辨率直接D和FFT的变换区间N有关，因为FFT能够实现的频率分辨率是$\frac{2\pi }{N}$，因此要求$\frac{2\pi }{N}\le D$。可以根据此式选择FFT的变换区间N。
（3）当N=8时，$x_3(n)$与$x_2(n)$的幅频特性会相同
当N=16时，$x_3(n)$与$x_2(n)$的幅频特性会不同