机器学习（聚类十）——谱聚类及代码实现

谱聚类是基于谱图理论基础上的一种聚类方法，与传统的聚类方法相比：具有在任意形状的样本空间上聚类并且收敛于全局最优解的优点。（但效率不高，实际工作中用的比较少）

谱聚类

通过对样本数据的拉普拉斯矩阵的特征向量进行聚类，从而达到对样本数据进行聚类的目的；其本质是将聚类问题转换为图的最优划分问题，是一种点对聚类算法。

谱聚类算法将数据集中的每个对象看做图的顶点 V，将顶点间的相似度量化为相应顶点连接边E的权值 w，这样就构成了一个基于相似度的无向加权图 G(V,E)，于是聚类问题就转换为图的划分问题。基于图的最优划分规则就是子图内的相似度最大，子图间的相似度最小。

步骤
谱聚类的构建过程主要包含以下几个步骤

• 构建表示对象相似度的矩阵 W
• 构建度矩阵 D(对角矩阵)
• 构建拉普拉斯矩阵 L（有个特点：行累加=0）
• 计算矩阵L的前 k 个特征值的特征向量(k 个列向量)
• 将k个列向量组成矩阵 U $\left(U_{n\times k}\right)$
• 对矩阵 U 中的 n 行数据利用 K-means 或其它经典聚类算法进行聚类得出最终结果

拉普拉斯矩阵及变形
$$W=(w_{ij})i,j=1,...,n$$

$$D=\left(\begin{array}{cccc}{\sum }_{i=1}^n{w}_{1j}& 0& 0& 0\\ ⋮& \ddots & ⋮& ⋮\\ 0& 0& {\sum }_{i=1}^n{w}_{ij}& 0\\ 0& 0& 0& {\sum }_{i=1}^n{w}_{nj}\end{array}\right)$$

$$L=D-W$$

• 拉普拉斯矩阵（算法默认使用的是拉普拉斯矩阵）
  $$L=D-W$$
• 对称拉普拉斯矩阵
  $$L_{sym}=D^{-\frac{1}{2}}(D-W)D^{-\frac{1}{2}}=I-D^{-\frac{1}{2}}W{D}^{-\frac{1}{2}}$$
• 随机游走拉普拉斯矩阵
  $$L_{r}w=D^{-1}(D-W)$$

应用场景
图形聚类、计算机视觉、非凸球形数据聚类等

面临的问题

• 相似度矩阵的构建问题（比较难）：业界一般使用高斯相似函数或者k近邻来作为相似度量，一般建议 使用k近邻的方式来计算相似度权值
• 聚类数目的给定
• 如何选择特征向量（矩阵一大，求特征向量的难度会比较高）
• 如何提高谱聚类的执行效率

代码实现

使用scikit的相关API创建模拟数据，然后使用谱聚类算法进行数据聚类操作，并比较算法在不同参数情况下的聚类效果。

API

sklearn.cluster.spectral_clustering(affinity, n_clusters=8, n_components=None, eigen_solver=None, random_state=None, n_init=10, eigen_tol=0.0, assign_labels=‘kmeans’)

参数

• affinity：相似度矩阵构建方式
• assign_labels：上面说的U的构建方式

代码

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
import warnings
from sklearn.cluster import spectral_clustering#引入谱聚类
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import euclidean_distances

## 设置属性防止中文乱码及拦截异常信息
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

warnings.filterwarnings('ignore', category=FutureWarning)

### 创建模拟数据
N = 1000
centers = [[1, 2], [-1, -1], [1, -1], [-1, 1]]
#符合高斯分布的数据集
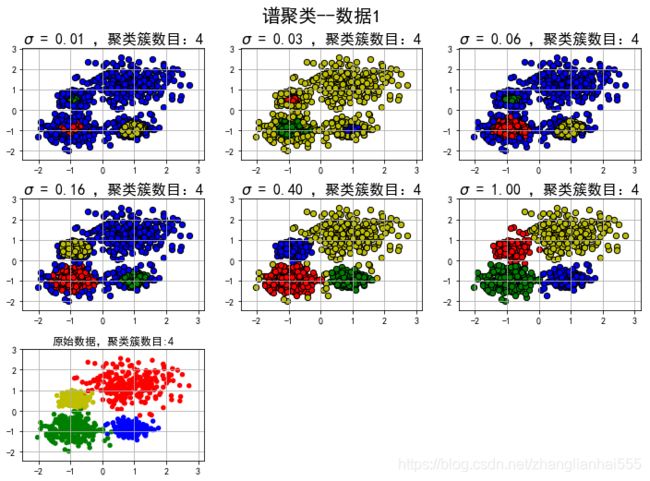
data1, y1 = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=(0.75,0.5,0.3,0.25), random_state=0)
data1 = StandardScaler().fit_transform(data1)
dist1 = euclidean_distances(data1, squared=True)
# 权重计算公式
affinity_params1 = map(lambda x: (x,np.exp(-dist1 ** 2 / (x ** 2)) + 1e-6), np.logspace(-2,0,6))

# 数据2
#圆形数据集
t = np.arange(0, 2 * np.pi, 0.1)
data2_1 = np.vstack((np.cos(t), np.sin(t))).T
data2_2 = np.vstack((2*np.cos(t), 2*np.sin(t))).T
data2_3 = np.vstack((3*np.cos(t), 3*np.sin(t))).T
data2 = np.vstack((data2_1, data2_2, data2_3))
y2 = np.vstack(([0] * len(data2_1), [1] * len(data2_2), [2] * len(data2_3)))
## 数据2的参数
dist2 = euclidean_distances(data2, squared=True)
affinity_params2 = map(lambda x: (x, np.exp(-dist2 ** 2 / (x ** 2)) + 1e-6), np.logspace(-2,0,6))

datasets = [(data1, y1, affinity_params1), (data2, y2, affinity_params2)]

def expandBorder(a, b):
    d = (b - a) * 0.1
    return a-d, b+d
colors = ['r', 'g', 'b', 'y']
cm = mpl.colors.ListedColormap(colors)

for i,(X, y, params) in enumerate(datasets):
    x1_min, x2_min = np.min(X, axis=0)
    x1_max, x2_max = np.max(X, axis=0)
    x1_min, x1_max = expandBorder(x1_min, x1_max)
    x2_min, x2_max = expandBorder(x2_min, x2_max)
    n_clusters = len(np.unique(y))
    plt.figure(figsize=(12, 8), facecolor='w')
    plt.suptitle(u'谱聚类--数据%d' % (i+1), fontsize=20)
    plt.subplots_adjust(top=0.9,hspace=0.35)
    
    for j,param in enumerate(params):
        sigma,af = param
        #谱聚类的建模
        ## af: 指定相似度矩阵构造方式(就是相似度矩阵)
        y_hat = spectral_clustering(af, n_clusters=n_clusters, assign_labels='kmeans', random_state=28)
        unique_y_hat = np.unique(y_hat)
        n_clusters = len(unique_y_hat) - (1 if -1 in y_hat else 0)
        print ("类别:",unique_y_hat,"；聚类簇数目:",n_clusters)
        
        ## 开始画图
        plt.subplot(3,3,j+1)
        for k, col in zip(unique_y_hat, colors):
            cur = (y_hat == k)
            plt.scatter(X[cur, 0], X[cur, 1], s=40, c=col, edgecolors='k')
        plt.xlim((x1_min, x1_max))
        plt.ylim((x2_min, x2_max))
        plt.grid(True)
        plt.title('$\sigma$ = %.2f ，聚类簇数目：%d' % (sigma, n_clusters), fontsize=16)

    plt.subplot(3,3,7)
    plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=cm, edgecolors='none')
    plt.xlim((x1_min, x1_max))
    plt.ylim((x2_min, x2_max))
    plt.title('原始数据，聚类簇数目:%d' % len(np.unique(y)))
    plt.grid(True)
    plt.show()  

类别: [0 1 2 3] ；聚类簇数目: 4
类别: [0 1 2 3] ；聚类簇数目: 4
类别: [0 1 2 3] ；聚类簇数目: 4
类别: [0 1 2 3] ；聚类簇数目: 4
类别: [0 1 2 3] ；聚类簇数目: 4
类别: [0 1 2 3] ；聚类簇数目: 4

类别: [0 1 2] ；聚类簇数目: 3
类别: [0 1 2] ；聚类簇数目: 3
类别: [0 1 2] ；聚类簇数目: 3
类别: [0 1 2] ；聚类簇数目: 3
类别: [0 1 2] ；聚类簇数目: 3
类别: [0 1 2] ；聚类簇数目: 3

上面提到“affinity：相似度矩阵构建方式”，可以使用高斯（相似度矩阵的构建问题，业界一般使用高斯相似函数或者k近邻来作为相似度量。）σ是高斯相似函数中的值