som神经网络聚类简单例子_机器学习算法推导&手写实现07——SOM网络
自组织特征映射神经网络(Self-Organizing Feature Map, 也称Kohonen网络),简称SOM网络。SOM网络是一种无监督学习算法,不同于一般神经网络基于损失函数的优化训练,SOM运用竞争学习策略逐步优化网络。其聚类的基本思想和KMeans算法相似,都是将距离小的个体集合划分为同一类别,将距离大的个体集合划分为不同的类别。
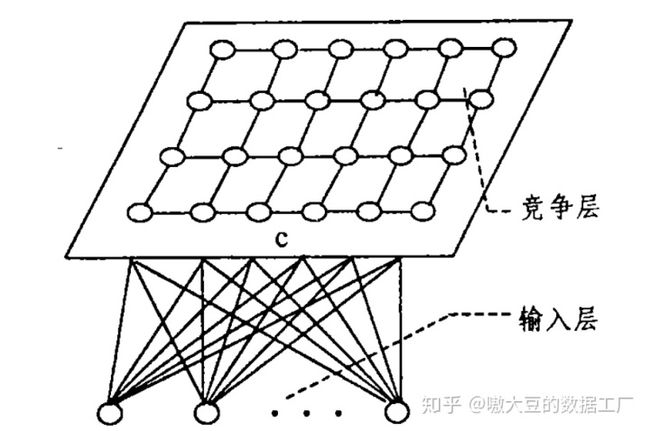
SOM网络结构比较简单,只有输入层和输出层(输出层我们通常也称为竞争层),在竞争层,神经元可以排列形成多种形式。每个样本都可以映射到与其距离最小的竞争层神经元上,最终在竞争层生成一个低维、离散的映射。结构如下图所示:
SOM网络推导
- SOM网络有一个特点在于竞争层的映射保留了原数据的拓扑结构。其样本之间的相对距离保持不变,举例来说原数据距离最近或者最远的,在新的映射下的距离还是最近或者最远的。具体我们也会在下面的代码画图给大家看下。
- 总的来说,SOM网络包含初始化、竞争、迭代三块内容。
首先是初始化过程。
1、归一化数据集。
2、设计竞争层结构。一般根据预估的聚类簇数进行设置。比如要分成4类,那我可以将竞争层设计为2*2,1*4,4*1。
3、预设竞争层神经元的权重节点。一般我们会根据输入数据的维度和竞争层预估的分类数来设置权重节点,若输入为二维数据,最终聚类为4类,则权重矩阵就是2*4。
4、初始化邻域半径、学习率。
其次是竞争过程。
1、随机选择样本,根据权重节点计算到竞争层每个神经元节点的距离。一般我们选择欧式距离公式求距离。
2、选择优胜节点。通过竞争,选择距离最小的神经元节点作为优胜节点。
然后是迭代过程。
1、圈定出优胜邻域内的所有节点。根据邻域半径,圈定出距离小于邻域半径的节点,形成优胜邻域。
圈定优胜邻域在这里需要注意的是,邻域半径影响着聚类效果,可以定义一个动态收缩的半径函数,随着迭代次数增加而不断收缩半径。具体函数我们定义如下:优胜半径的迭代公式
2、对优胜邻域内的节点权重进行迭代更新。更新的思想是越靠近优胜节点,更新幅度越大;越远离优胜节点,更新幅度越小,故我们需要对不同的节点增加一个更新约束,一般可以高斯函数求得。另外我们更新节点的目的是为了使得优胜节点更加逼近样本点,故在节点权重的更新上,我们采用以下公式:
神经元节点权重迭代公式在这里同样需要注意的是,学习率影响着收敛速度和收敛结果,所以也可以定义一个动态收缩的学习率函数,随着迭代次数增加而不断减小学习率。其函数与领域半径函数类似,在此就不再赘述。
最后重复竞争、迭代步骤,直至迭代结束。
以上是SOM网络的推导部分。
Python实现SOM网络
在代码这部分中,有以下几项内容:
- 1、Python手写实现SOM网络。
- 2、利用自己手写的类对一个二维数据集进行聚类分析。
- 3、利用自己手写的类和第三方库minisom,分别对鸢尾花的数据进行映射,并查看映射后的拓扑关系。
首先是手写SOM网络部分。
- 我们先来构造一个SOM类。
import numpy as np
import os
#os.chdir(r"D:myworktest")
class SOMnetwork(object):
"""
Self-Organizing Feature Map
"""
def __init__(self, maxRound, minRound, maxRate, minRate, Iters):
self.maxRound = maxRound
self.minRound = minRound
self.maxRate = maxRate
self.minRate = minRate
self.steps = Iters
self.RateList = [] #存放每轮迭代学习率的容器
self.RoundList = [] #存放每轮迭代优胜半径的容器
self.X = 0 #训练数据集
self.normX = 0 #归一化后的数据集
self.gridLocation = 0 #竞争层的神经元节点位置坐标
self.w = 0 #神经元节点权重
self.gridDist = 0 #神经元节点之间的距离- 然后我们设置了一些函数,包括:归一化原始数据函数、计算欧式距离函数、计算各个神经元节点之间距离的函数、初始化竞争层节点权重函数。
#归一化函数
def normalize(self,X):
return (X-X.min(axis=0))/(X.max(axis=0)-X.min(axis=0))
#计算欧式距离函数
def edist(self,X1,X2):
return (np.linalg.norm(X1-X2))
#计算各个节点之间的距离
def calGdist(self, grid):
m = len(grid)
Gdist = np.zeros((m,m))
for i in range(m):
for j in range(m):
if i != j:
Gdist[i,j] = self.edist(grid[i], grid[j])
return Gdist
#初始化竞争层
def init_grid(self,M,N):
grid = np.zeros((M*N,2)) #分成M*N类,两个维度
k = 0
for i in range(M):
for j in range(N):
grid[k,:] = np.array([i,j])
k += 1
return grid- 在这里我们还设置了学习率和优胜半径的递减函数。
#学习率和优胜半径的递减函数
def changeRate(self,i):
Rate = self.maxRate - (self.maxRate-self.minRate)*(i+1)/self.steps
Round = self.maxRound - (self.maxRound-self.minRound)*(i+1)/self.steps
return Rate, Round- 接着是模型训练的主体部分,用来训练得出最终的竞争层的神经元节点的权重。在这里为了简化计算这里暂不考虑节点的更新约束。
#开始训练
def train(self, X, M, N):
self.X = X
##标准化数据集
X = self.normalize(X)
n_samples, n_features = X.shape
##1 初始化
###各个节点位置,以及各节点之间的位置
self.gridLocation = self.init_grid(M,N)
self.gridDist = self.calGdist(self.gridLocation)
###初始化各个节点对应的权值
w = np.random.random((M*N, n_features))
###确定迭代次数,不小于样本数的5倍
if self.steps<5*n_samples:
self.steps = 5*n_samples
for i in range(self.steps):
##2 竞争
###随机选取样本计算距离
data = X[np.random.randint(0, n_samples, 1)[0], :]
Xdist = [self.edist(data,w[row]) for row in range(len(w))]
###找到优胜节点
winnerPointIdx = Xdist.index(min(Xdist))
##3 迭代
###确定学习率和节点优胜半径,并保存
Rate, Round = self.changeRate(i)
self.RateList.append(Rate)
self.RoundList.append(Round)
###圈定优胜邻域内的所有节点
winnerRoundIdx = np.nonzero(self.gridDist[winnerPointIdx]- 最后少不了聚类的函数,根据训练出来的权重,将数据集进行聚类。
#聚类标签
def cluster(self, X):
X = self.normalize(X)
m = X.shape[0]
cluster_labels = []
for i in range(m):
yi = np.linalg.norm((X[i] - self.w), axis=1)
cluster_labels.append(yi.argmin())
return np.array(cluster_labels)其次我们利用手写的SOM网络类来对数据集进行聚类测试。
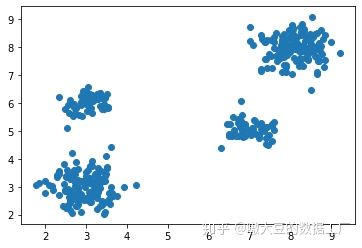
- 我们先导入数据,看下分布。我们发现这样的数据做出来的结果好坏应该很好分辨。
if __name__ == "__main__":
#####################################################
# #
# 自编的SOM网络对二维数据进行聚类测试 #
# #
#####################################################
#用于聚类的数据准备
with open("somSet.txt") as f:
trainSet = f.readlines()
trainSet = np.array([line.split("t") for line in trainSet]).astype(float)
#查看下数据分布
import matplotlib.pyplot as plt
plt.scatter(trainSet[:,0], trainSet[:,1])
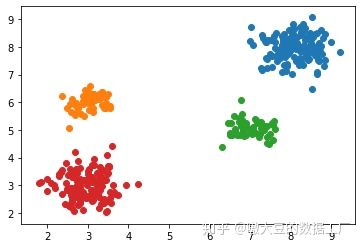
plt.show()- 接着我们进行训练,并再次画图验证聚类结果。我们发现聚类结果正确无误。
#正式SOM聚类
som_self = SOMnetwork(5, 0.1, 0.5, 0.01, 1000)
som_self.train(trainSet, 2, 2)
som_self_cluster = som_self.cluster(trainSet)
#再次画图验证聚类结果
for cc in set(som_self_cluster):
plt.scatter(trainSet[som_self_cluster==cc,0], trainSet[som_self_cluster==cc,1])
plt.show()最后我们需要通过自编的SOM网络和minisom第三方库中的SOM网络分别对鸢尾花数据集(IRIS)进行聚类映射,并查看其映射后结果在二维平面上的拓扑结构。
- 先是自编的SOM网络,我们都选择将数据集映射到6*6的平面中,也就是说最多可以聚成36类。
#####################################################
# #
# 自编的SOM网络和minisom第三方库测试iris数据集 #
# #
#####################################################
#导入Iris数据集
from sklearn.datasets import load_iris
X, y = load_iris(True)
#自编的SOM网络对Iris进行6*6的映射
n = 6
som_self = SOMnetwork(5, 0.1, 0.5, 0.01, 1000)
som_self.train(X, n, n)
som_self_cluster = som_self.cluster(X)
som_grid = som_self.gridLocation
som_grid_Idx = [(som_grid[i,0], som_grid[i,1]) for i in range(som_grid.shape[0])]- 我们看下映射后的拓扑结构图。
import matplotlib.pyplot as plt
def draw(y, cluster, m, n, gridLocation):
yset = np.unique(y)
fig = plt.figure(dpi=100)
for i in range(gridLocation.shape[0]):
labelisi = sum(cluster==i)
if labelisi > 0:
#统计映射后的每个真实标签的个数
yi = y[cluster==i]
yiCount = np.bincount(yi)
#统计比率
if yiCount.size < yset.size:
yiCount = yiCount.tolist() + [0]*(yset.size-yiCount.size)
yiRatio = yiCount/labelisi
plt.subplot(n, n, i+1)
plt.pie(yiRatio)
plt.text(x=0, y=0, s=str(labelisi), fontsize=15, horizontalalignment='center', verticalalignment='center')
fig.legend(yset)
plt.show()
#自编的SOM网络结果画平面的拓扑图
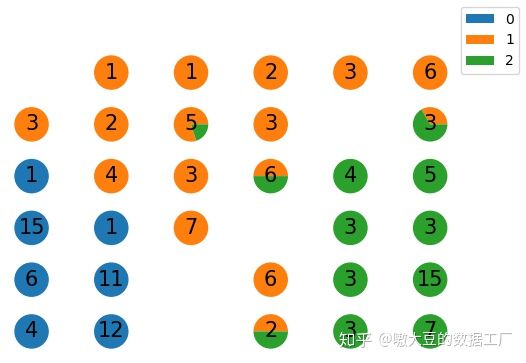
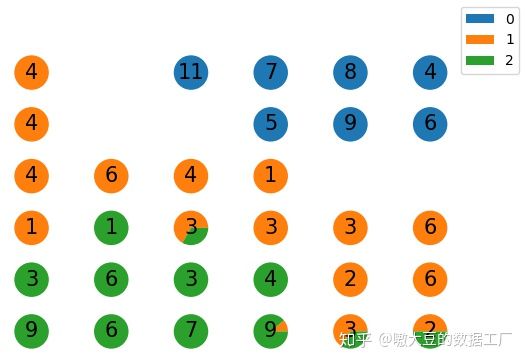
draw(y, som_self_cluster, n, n, som_grid)- 我们对图片解释下,便于大家理解SOM网络中的知识点。首先这里的【0,1,2】表示的是鸢尾花数据集自身的真实分类标签;然后图里的饼图代表着不同的神经元节点类型(聚类类型);上面的数字代表着在这一个节点上的样本数量(被聚为一类的数量)。
通过图,我们可以发现2点:
第一点是,虽然我们预设了6*6,共36类,但是我们可以发现,有几个节点是没有样本的,这就是SOM网络特殊的地方,在Kmeans中一般我们指定了K类,最终大概率会有K类聚类的返还,但在SOM网络中由于其自身的适应性,会自动调整聚类结果。
第二点是,映射后的新的数据的确会保留数据原有的拓扑结构,虽然没有完全映射到一个节点中,但是其最终映射的多个节点任然是紧凑的挨在一起。
- 最后我们也看下第三方库minisom的聚类结果。
#minisom第三方库的结果
from minisom import MiniSom
som_minisom = MiniSom(n, n, X.shape[1])
som_minisom.train_random(X, 1000)
som_minisom_cluster = np.array([som_grid_Idx.index(list(som_minisom.win_map(np.expand_dims(X[i],0)).keys())[0]) for i in range(X.shape[0])])
#minisom第三方库的SOM网络结果画平面的拓扑图
draw(y, som_minisom_cluster, n, n, som_grid)以上就是本次SOM网络的全部内容,谢谢阅读。
全部代码可前往以下地址下载:
shoucangjia1qu/ML_gzhgithub.com往期回顾:
机器学习算法推导&手写实现06——RBF网络
机器学习算法推导&手写实现05——BP神经网络
机器学习算法推导&手写实现04——感知机
机器学习算法推导&手写实现03——线性判别分析
机器学习算法推导&手写实现02——逻辑斯蒂回归
机器学习算法推导&手写实现01——线性回归
优化算法推导&手写实现——牛顿法和拟牛顿法2
优化算法推导&手写实现——牛顿法和拟牛顿法1
学无止境,欢迎关注笔者公众号(嗷大豆的数据工厂),互相学习。
http://weixin.qq.com/r/VylAWMbEx5u4rYI793xF (二维码自动识别)