3.2 图像分类
文章目录
- LeNet(小图像)
-
- LeNet在手写数字识别上的应用
- LeNet在眼疾识别数据集iChallenge-PM上的应用
-
- 数据集准备
- 查看数据集图片
- 定义数据读取器
-
- 启动训练
- AlexNet(大图像)
- VGG(深度)
- GoogLeNet(深度兼广度)
- ResNet
-
- 使用飞桨高层API直接调用图像分类网络
- 小结
**图像分类是根据图像的语义信息对不同类别图像进行区分,是计算机视觉的核心,是物体检测、图像分割、物体跟踪、行为分析、人脸识别等其他高层次视觉任务的基础。**图像分类在许多领域都有着广泛的应用,如:安防领域的人脸识别和智能视频分析等,交通领域的交通场景识别,互联网领域基于内容的图像检索和相册自动归类,医学领域的图像识别等。
上一节主要介绍了卷积神经网络常用的一些基本模块,**本节将基于眼疾分类数据集iChallenge-PM,对图像分类领域的经典卷积神经网络进行剖析,介绍如何应用这些基础模块构建卷积神经网络,解决图像分类问题。**按照被提出的时间顺序,涵盖如下卷积神经网络:
-
LeNet:Yan LeCun等人于1998年第一次将卷积神经网络应用到图像分类任务上[1],在手写数字识别任务上取得了巨大成功。
-
AlexNet:Alex Krizhevsky等人在2012年提出了AlexNet[2], 并应用在大尺寸图片数据集ImageNet上,获得了2012年ImageNet比赛冠军(ImageNet Large Scale Visual Recognition Challenge,ILSVRC)。
-
VGG:Simonyan和Zisserman于2014年提出了VGG网络结构[3],是当前最流行的卷积神经网络之一,由于其结构简单、应用性极强而深受广大研究者欢迎。
-
GoogLeNet:Christian Szegedy等人在2014提出了GoogLeNet[4],并取得了2014年ImageNet比赛冠军。
-
ResNet:Kaiming He等人在2015年提出了ResNet[5],通过引入残差模块加深网络层数,在ImagNet数据集上的错误率降低到3.6%,超越了人眼识别水平。ResNet的设计思想深刻地影响了后来的深度神经网络的设计。
LeNet(小图像)
LeNet是最早的卷积神经网络之一[1]。1998年,Yann LeCun第一次将LeNet卷积神经网络应用到图像分类上,在手写数字识别任务中取得了巨大成功。LeNet通过连续使用卷积和池化层的组合提取图像特征,其架构如 图1 所示,这里展示的是用于MNIST手写体数字识别任务中的LeNet-5模型:
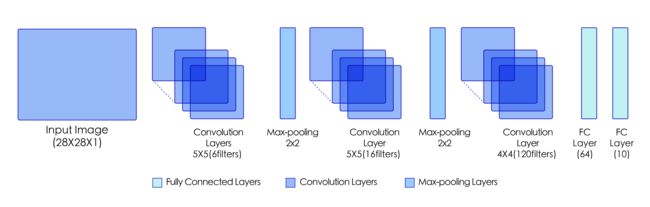
图1:LeNet模型网络结构示意图
-
第一模块:包含5×5的6通道卷积和2×2的池化。卷积提取图像中包含的特征模式(激活函数使用Sigmoid),图像尺寸从28减小到24。经过池化层可以降低输出特征图对空间位置的敏感性,图像尺寸减到12。
-
第二模块:和第一模块尺寸相同,通道数由6增加为16。卷积操作使图像尺寸减小到8,经过池化后变成4。
-
第三模块:包含4×4的120通道卷积。卷积之后的图像尺寸减小到1,但是通道数增加为120。将经过第3次卷积提取到的特征图输入到全连接层。第一个全连接层的输出神经元的个数是64,第二个全连接层的输出神经元个数是分类标签的类别数,对于手写数字识别的类别数是10。然后使用Softmax激活函数即可计算出每个类别的预测概率。
【提示】:
卷积层的输出特征图如何当作全连接层的输入使用呢?
卷积层的输出数据格式是 [ N , C , H , W ] [N, C, H, W] [N,C,H,W],在输入全连接层的时候,会自动将数据拉平,也就是对每个样本,自动将其转化为长度为 K K K的向量,其中 K = C × H × W K = C \times H \times W K=C×H×W,一个mini-batch的数据维度变成了 N × K N\times K N×K的二维向量。
LeNet在手写数字识别上的应用
LeNet网络的实现代码如下:
# 导入需要的包
import paddle
import numpy as np
from paddle.nn import Conv2D, MaxPool2D, Linear
## 组网
import paddle.nn.functional as F
# 定义 LeNet 网络结构
class LeNet(paddle.nn.Layer):
def __init__(self, num_classes=1):
super(LeNet, self).__init__()
# 创建卷积和池化层
# 创建第1个卷积层
self.conv1 = Conv2D(in_channels=1, out_channels=6, kernel_size=5)
self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)
# 尺寸的逻辑:池化层未改变通道数;当前通道数为6
# 创建第2个卷积层
self.conv2 = Conv2D(in_channels=6, out_channels=16, kernel_size=5)
self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)
# 创建第3个卷积层
self.conv3 = Conv2D(in_channels=16, out_channels=120, kernel_size=4)
# 尺寸的逻辑:输入层将数据拉平[B,C,H,W] -> [B,C*H*W]
# 输入size是[28,28],经过三次卷积和两次池化之后,C*H*W等于120
self.fc1 = Linear(in_features=120, out_features=64)
# 创建全连接层,第一个全连接层的输出神经元个数为64, 第二个全连接层输出神经元个数为分类标签的类别数
self.fc2 = Linear(in_features=64, out_features=num_classes)
# 网络的前向计算过程
def forward(self, x):
x = self.conv1(x)
# 每个卷积层使用Sigmoid激活函数,后面跟着一个2x2的池化
x = F.sigmoid(x)
x = self.max_pool1(x)
x = F.sigmoid(x)
x = self.conv2(x)
x = self.max_pool2(x)
x = self.conv3(x)
# 尺寸的逻辑:输入层将数据拉平[B,C,H,W] -> [B,C*H*W]
x = paddle.reshape(x, [x.shape[0], -1])
x = self.fc1(x)
x = F.sigmoid(x)
x = self.fc2(x)
return x
**飞桨会根据实际图像数据的尺寸和卷积核参数自动推断中间层数据的W和H等,只需要用户表达通道数即可。**下面的程序使用随机数作为输入,查看经过LeNet-5的每一层作用之后,输出数据的形状。
# 输入数据形状是 [N, 1, H, W]
# 这里用np.random创建一个随机数组作为输入数据
x = np.random.randn(*[3,1,28,28])
x = x.astype('float32')
# 创建LeNet类的实例,指定模型名称和分类的类别数目
model = LeNet(num_classes=10)
# 通过调用LeNet从基类继承的sublayers()函数,
# 查看LeNet中所包含的子层
print(model.sublayers())
x = paddle.to_tensor(x)
for item in model.sublayers():
# item是LeNet类中的一个子层
# 查看经过子层之后的输出数据形状
try:
x = item(x)
except:
x = paddle.reshape(x, [x.shape[0], -1])
x = item(x)
if len(item.parameters())==2:
# 查看卷积和全连接层的数据和参数的形状,
# 其中item.parameters()[0]是权重参数w,item.parameters()[1]是偏置参数b
print(item.full_name(), x.shape, item.parameters()[0].shape, item.parameters()[1].shape)
else:
# 池化层没有参数
print(item.full_name(), x.shape)
[Conv2D(1, 6, kernel_size=[5, 5], data_format=NCHW), MaxPool2D(kernel_size=2, stride=2, padding=0), Conv2D(6, 16, kernel_size=[5, 5], data_format=NCHW), MaxPool2D(kernel_size=2, stride=2, padding=0), Conv2D(16, 120, kernel_size=[4, 4], data_format=NCHW), Linear(in_features=120, out_features=64, dtype=float32), Linear(in_features=64, out_features=10, dtype=float32)]
conv2d_0 [3, 6, 24, 24] [6, 1, 5, 5] [6]
max_pool2d_0 [3, 6, 12, 12]
conv2d_1 [3, 16, 8, 8] [16, 6, 5, 5] [16]
max_pool2d_1 [3, 16, 4, 4]
conv2d_2 [3, 120, 1, 1] [120, 16, 4, 4] [120]
linear_0 [3, 64] [120, 64] [64]
linear_1 [3, 10] [64, 10] [10]
卷积Conv2D的padding参数默认为0,stride参数默认为1,当输入形状为[Bx1x28x28]时,B是batch_size,经过第一层卷积(kernel_size=5, out_channels=6)和maxpool之后,得到形状为[Bx6x12x12]的特征图;经过第二层卷积(kernel_size=5, out_channels=16)和maxpool之后,得到形状为[Bx16x4x4]的特征图;经过第三层卷积(out_channels=120, kernel_size=4)之后,得到形状为[Bx120x1x1]的特征图,在FC层计算之前,将输入特征从卷积得到的四维特征reshape到格式为[B, 120x1x1]的特征,这也是LeNet中第一层全连接层输入shape为120的原因。
# -*- coding: utf-8 -*-
# LeNet 识别手写数字
import os
import random
import paddle
import numpy as np
import paddle
from paddle.vision.transforms import ToTensor
from paddle.vision.datasets import MNIST
# 定义训练过程
def train(model, opt, train_loader, valid_loader):
# 开启0号GPU训练
use_gpu = True
paddle.device.set_device('gpu:0') if use_gpu else paddle.device.set_device('cpu')
print('start training ... ')
model.train()
for epoch in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
img = data[0]
label = data[1]
# 计算模型输出
logits = model(img)
# 计算损失函数
loss_func = paddle.nn.CrossEntropyLoss(reduction='none')
loss = loss_func(logits, label)
avg_loss = paddle.mean(loss)
if batch_id % 2000 == 0:
print("epoch: {}, batch_id: {}, loss is: {:.4f}".format(epoch, batch_id, float(avg_loss.numpy())))
avg_loss.backward()
opt.step()
opt.clear_grad()
model.eval()
accuracies = []
losses = []
for batch_id, data in enumerate(valid_loader()):
img = data[0]
label = data[1]
# 计算模型输出
logits = model(img)
pred = F.softmax(logits)
# 计算损失函数
loss_func = paddle.nn.CrossEntropyLoss(reduction='none')
loss = loss_func(logits, label)
acc = paddle.metric.accuracy(pred, label)
accuracies.append(acc.numpy())
losses.append(loss.numpy())
print("[validation] accuracy/loss: {:.4f}/{:.4f}".format(np.mean(accuracies), np.mean(losses)))
model.train()
# 保存模型参数
paddle.save(model.state_dict(), 'mnist.pdparams')
# 创建模型
model = LeNet(num_classes=10)
# 设置迭代轮数
EPOCH_NUM = 5
# 设置优化器为Momentum,学习率为0.001
opt = paddle.optimizer.Momentum(learning_rate=0.001, momentum=0.9, parameters=model.parameters())
# 定义数据读取器
train_loader = paddle.io.DataLoader(MNIST(mode='train', transform=ToTensor()), batch_size=10, shuffle=True)
valid_loader = paddle.io.DataLoader(MNIST(mode='test', transform=ToTensor()), batch_size=10)
# 启动训练过程
train(model, opt, train_loader, valid_loader)
start training ...
epoch: 0, batch_id: 0, loss is: 2.5242
epoch: 0, batch_id: 2000, loss is: 2.2943
epoch: 0, batch_id: 4000, loss is: 1.8200
[validation] accuracy/loss: 0.8411/0.6527
epoch: 1, batch_id: 0, loss is: 0.6084
epoch: 1, batch_id: 2000, loss is: 0.4534
epoch: 1, batch_id: 4000, loss is: 0.1083
[validation] accuracy/loss: 0.9098/0.3208
epoch: 2, batch_id: 0, loss is: 0.3667
epoch: 2, batch_id: 2000, loss is: 0.1954
epoch: 2, batch_id: 4000, loss is: 0.3011
[validation] accuracy/loss: 0.9275/0.2395
epoch: 3, batch_id: 0, loss is: 0.1407
epoch: 3, batch_id: 2000, loss is: 0.7692
epoch: 3, batch_id: 4000, loss is: 0.1613
[validation] accuracy/loss: 0.9470/0.1795
epoch: 4, batch_id: 0, loss is: 0.0142
epoch: 4, batch_id: 2000, loss is: 0.0407
epoch: 4, batch_id: 4000, loss is: 0.0497
[validation] accuracy/loss: 0.9577/0.1487
通过运行结果可以看出,LeNet在手写数字识别MNIST验证数据集上的准确率高达92%以上。那么对于其它数据集效果如何呢?我们通过眼疾识别数据集iChallenge-PM验证一下。
LeNet在眼疾识别数据集iChallenge-PM上的应用
iChallenge-PM是百度大脑和中山大学中山眼科中心联合举办的iChallenge比赛中,提供的关于病理性近视(Pathologic Myopia,PM)的医疗类数据集,包含1200个受试者的眼底视网膜图片,训练、验证和测试数据集各400张。下面我们详细介绍LeNet在iChallenge-PM上的训练过程。
说明:
如今近视已经成为困扰人们健康的一项全球性负担,在近视人群中,有超过35%的人患有重度近视。近视会拉长眼睛的光轴,也可能引起视网膜或者络网膜的病变。随着近视度数的不断加深,高度近视有可能引发病理性病变,这将会导致以下几种症状:视网膜或者络网膜发生退化、视盘区域萎缩、漆裂样纹损害、Fuchs斑等。因此,及早发现近视患者眼睛的病变并采取治疗,显得非常重要。
数据可以从AI Studio下载
数据集准备
/home/aistudio/data/data19065 目录包括如下三个文件,解压缩后存放在/home/aistudio/work/palm目录下。
- training.zip:包含训练中的图片和标签
- validation.zip:包含验证集的图片
- valid_gt.zip:包含验证集的标签
注意:
valid_gt.zip文件解压缩之后,需要将“/home/aistudio/work/palm/PALM-Validation-GT/”目录下的“PM_Label_and_Fovea_Location.xlsx”文件转存成.csv格式,本节代码示例中已经提前转成文件labels.csv。
# 初次运行时将注释取消,以便解压文件
# 如果已经解压过,不需要运行此段代码,否则由于文件已经存在,解压时会报错
!unzip -o -q -d /home/aistudio/work/palm /home/aistudio/data/data19065/training.zip
%cd /home/aistudio/work/palm/PALM-Training400/
!unzip -o -q PALM-Training400.zip
!unzip -o -q -d /home/aistudio/work/palm /home/aistudio/data/data19065/validation.zip
!unzip -o -q -d /home/aistudio/work/palm /home/aistudio/data/data19065/valid_gt.zip
#返回家目录,生成模型文件位于/home/aistudio/
%cd /home/aistudio/
查看数据集图片
iChallenge-PM中既有病理性近视患者的眼底图片,也有非病理性近视患者的图片,命名规则如下:
-
病理性近视(PM):文件名以P开头
-
非病理性近视(non-PM):
-
高度近视(high myopia):文件名以H开头
-
正常眼睛(normal):文件名以N开头
-
**我们将病理性患者的图片作为正样本,标签为1; 非病理性患者的图片作为负样本,标签为0。**从数据集中选取两张图片,通过LeNet提取特征,构建分类器,对正负样本进行分类,并将图片显示出来。代码如下所示:
import os
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from PIL import Image
DATADIR = '/home/aistudio/work/palm/PALM-Training400/PALM-Training400'
# 文件名以N开头的是正常眼底图片,以P开头的是病变眼底图片
file1 = 'N0012.jpg'
file2 = 'P0095.jpg'
# 读取图片
img1 = Image.open(os.path.join(DATADIR, file1))
img1 = np.array(img1)
img2 = Image.open(os.path.join(DATADIR, file2))
img2 = np.array(img2)
# 画出读取的图片
plt.figure(figsize=(8, 3))
f = plt.subplot(121)
f.set_title('Normal', fontsize=20)
plt.imshow(img1)
f = plt.subplot(122)
f.set_title('PM', fontsize=20)
plt.imshow(img2)
plt.show()
# 查看图片形状
img1.shape, img2.shape
((2056, 2124, 3), (2056, 2124, 3))
定义数据读取器
使用OpenCV从磁盘读入图片,将每张图缩放到 224 × 224 224\times224 224×224大小,并且将像素值调整到 [ − 1 , 1 ] [-1, 1] [−1,1]之间,代码如下所示:
import cv2
import random
import numpy as np
import os
# 对读入的图像数据进行预处理
def transform_img(img):
# 将图片尺寸缩放道 224x224
img = cv2.resize(img, (224, 224))
# 读入的图像数据格式是[H, W, C]
# 使用转置操作将其变成[C, H, W]
img = np.transpose(img, (2,0,1))
img = img.astype('float32')
# 将数据范围调整到[-1.0, 1.0]之间
img = img / 255.
img = img * 2.0 - 1.0
return img
# 定义训练集数据读取器
def data_loader(datadir, batch_size=10, mode = 'train'):
# 将datadir目录下的文件列出来,每条文件都要读入
filenames = os.listdir(datadir)
def reader():
if mode == 'train':
# 训练时随机打乱数据顺序
random.shuffle(filenames)
batch_imgs = []
batch_labels = []
for name in filenames:
filepath = os.path.join(datadir, name)
img = cv2.imread(filepath)
img = y'yyy(img)
if name[0] == 'H' or name[0] == 'N':
# H开头的文件名表示高度近似,N开头的文件名表示正常视力
# 高度近视和正常视力的样本,都不是病理性的,属于负样本,标签为0
label = 0
elif name[0] == 'P':
# P开头的是病理性近视,属于正样本,标签为1
label = 1
else:
raise('Not excepted file name')
# 每读取一个样本的数据,就将其放入数据列表中
batch_imgs.append(img)
batch_labels.append(label)
if len(batch_imgs) == batch_size:
# 当数据列表的长度等于batch_size的时候,
# 把这些数据当作一个mini-batch,并作为数据生成器的一个输出
imgs_array = np.array(batch_imgs).astype('float32')
labels_array = np.array(batch_labels).astype('float32').reshape(-1, 1)
yield imgs_array, labels_array
batch_imgs = []
batch_labels = []
if len(batch_imgs) > 0:
# 剩余样本数目不足一个batch_size的数据,一起打包成一个mini-batch
imgs_array = np.array(batch_imgs).astype('float32')
labels_array = np.array(batch_labels).astype('float32').reshape(-1, 1)
yield imgs_array, labels_array
return reader
# 定义验证集数据读取器
def valid_data_loader(datadir, csvfile, batch_size=10, mode='valid'):
# 训练集读取时通过文件名来确定样本标签,验证集则通过csvfile来读取每个图片对应的标签
# 请查看解压后的验证集标签数据,观察csvfile文件里面所包含的内容
# csvfile文件所包含的内容格式如下,每一行代表一个样本,
# 其中第一列是图片id,第二列是文件名,第三列是图片标签,
# 第四列和第五列是Fovea的坐标,与分类任务无关
# ID,imgName,Label,Fovea_X,Fovea_Y
# 1,V0001.jpg,0,1157.74,1019.87
# 2,V0002.jpg,1,1285.82,1080.47
# 打开包含验证集标签的csvfile,并读入其中的内容
filelists = open(csvfile).readlines()
def reader():
batch_imgs = []
batch_labels = []
for line in filelists[1:]:
line = line.strip().split(',')
name = line[1]
label = int(line[2])
# 根据图片文件名加载图片,并对图像数据作预处理
filepath = os.path.join(datadir, name)
img = cv2.imread(filepath)
img = transform_img(img)
# 每读取一个样本的数据,就将其放入数据列表中
batch_imgs.append(img)
batch_labels.append(label)
if len(batch_imgs) == batch_size:
# 当数据列表的长度等于batch_size的时候,
# 把这些数据当作一个mini-batch,并作为数据生成器的一个输出
imgs_array = np.array(batch_imgs).astype('float32')
labels_array = np.array(batch_labels).astype('float32').reshape(-1, 1)
yield imgs_array, labels_array
batch_imgs = []
batch_labels = []
if len(batch_imgs) > 0:
# 剩余样本数目不足一个batch_size的数据,一起打包成一个mini-batch
imgs_array = np.array(batch_imgs).astype('float32')
labels_array = np.array(batch_labels).astype('float32').reshape(-1, 1)
yield imgs_array, labels_array
return reader
# 查看数据形状
DATADIR = '/home/aistudio/work/palm/PALM-Training400/PALM-Training400'
train_loader = data_loader(DATADIR,
batch_size=10, mode='train')
data_reader = train_loader()
data = next(data_reader)
data[0].shape, data[1].shape
eval_loader = data_loader(DATADIR,
batch_size=10, mode='eval')
data_reader = eval_loader()
data = next(data_reader)
data[0].shape, data[1].shape
((10, 3, 224, 224), (10, 1))
启动训练
# -*- coding: utf-8 -*-
# LeNet 识别眼疾图片
import os
import random
import paddle
import numpy as np
DATADIR = '/home/aistudio/work/palm/PALM-Training400/PALM-Training400'
DATADIR2 = '/home/aistudio/work/palm/PALM-Validation400'
CSVFILE = '/home/aistudio/labels.csv'
# 设置迭代轮数
EPOCH_NUM = 5
# 定义训练过程
def train_pm(model, optimizer):
# 开启0号GPU训练
use_gpu = True
paddle.device.set_device('gpu:0') if use_gpu else paddle.device.set_device('cpu')
print('start training ... ')
model.train()
# 定义数据读取器,训练数据读取器和验证数据读取器
train_loader = data_loader(DATADIR, batch_size=10, mode='train')
valid_loader = valid_data_loader(DATADIR2, CSVFILE)
for epoch in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
x_data, y_data = data
img = paddle.to_tensor(x_data)
label = paddle.to_tensor(y_data)
# 运行模型前向计算,得到预测值
logits = model(img)
loss = F.binary_cross_entropy_with_logits(logits, label)
avg_loss = paddle.mean(loss)
if batch_id % 20 == 0:
print("epoch: {}, batch_id: {}, loss is: {:.4f}".format(epoch, batch_id, float(avg_loss.numpy())))
# 反向传播,更新权重,清除梯度
avg_loss.backward()
optimizer.step()
optimizer.clear_grad()
model.eval()
accuracies = []
losses = []
for batch_id, data in enumerate(valid_loader()):
x_data, y_data = data
img = paddle.to_tensor(x_data)
label = paddle.to_tensor(y_data)
# 运行模型前向计算,得到预测值
logits = model(img)
# 二分类,sigmoid计算后的结果以0.5为阈值分两个类别
# 计算sigmoid后的预测概率,进行loss计算
pred = F.sigmoid(logits)
loss = F.binary_cross_entropy_with_logits(logits, label)
# 计算预测概率小于0.5的类别
pred2 = pred * (-1.0) + 1.0
# 得到两个类别的预测概率,并沿第一个维度级联
pred = paddle.concat([pred2, pred], axis=1)
acc = paddle.metric.accuracy(pred, paddle.cast(label, dtype='int64'))
accuracies.append(acc.numpy())
losses.append(loss.numpy())
print("[validation] accuracy/loss: {:.4f}/{:.4f}".format(np.mean(accuracies), np.mean(losses)))
model.train()
paddle.save(model.state_dict(), 'palm.pdparams')
paddle.save(optimizer.state_dict(), 'palm.pdopt')
# 定义评估过程
def evaluation(model, params_file_path):
# 开启0号GPU预估
use_gpu = True
paddle.device.set_device('gpu:0') if use_gpu else paddle.device.set_device('cpu')
print('start evaluation .......')
#加载模型参数
model_state_dict = paddle.load(params_file_path)
model.load_dict(model_state_dict)
model.eval()
eval_loader = data_loader(DATADIR,
batch_size=10, mode='eval')
acc_set = []
avg_loss_set = []
for batch_id, data in enumerate(eval_loader()):
x_data, y_data = data
img = paddle.to_tensor(x_data)
label = paddle.to_tensor(y_data)
y_data = y_data.astype(np.int64)
label_64 = paddle.to_tensor(y_data)
# 计算预测和精度
prediction, acc = model(img, label_64)
# 计算损失函数值
loss = F.binary_cross_entropy_with_logits(prediction, label)
avg_loss = paddle.mean(loss)
acc_set.append(float(acc.numpy()))
avg_loss_set.append(float(avg_loss.numpy()))
# 求平均精度
acc_val_mean = np.array(acc_set).mean()
avg_loss_val_mean = np.array(avg_loss_set).mean()
print('loss={:.4f}, acc={:.4f}'.format(avg_loss_val_mean, acc_val_mean))
# -*- coding:utf-8 -*-
# 导入需要的包
import paddle
import numpy as np
from paddle.nn import Conv2D, MaxPool2D, Linear, Dropout
import paddle.nn.functional as F
# 定义 LeNet 网络结构
class LeNet(paddle.nn.Layer):
def __init__(self, num_classes=1):
super(LeNet, self).__init__()
# 创建卷积和池化层块,每个卷积层使用Sigmoid激活函数,后面跟着一个2x2的池化
self.conv1 = Conv2D(in_channels=3, out_channels=6, kernel_size=5)
self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)
self.conv2 = Conv2D(in_channels=6, out_channels=16, kernel_size=5)
self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)
# 创建第3个卷积层
self.conv3 = Conv2D(in_channels=16, out_channels=120, kernel_size=4)
# 创建全连接层,第一个全连接层的输出神经元个数为64
self.fc1 = Linear(in_features=300000, out_features=64)
# 第二个全连接层输出神经元个数为分类标签的类别数
self.fc2 = Linear(in_features=64, out_features=num_classes)
# 网络的前向计算过程
def forward(self, x, label=None):
x = self.conv1(x)
x = F.sigmoid(x)
x = self.max_pool1(x)
x = self.conv2(x)
x = F.sigmoid(x)
x = self.max_pool2(x)
x = self.conv3(x)
x = F.sigmoid(x)
x = paddle.reshape(x, [x.shape[0], -1])
x = self.fc1(x)
x = F.sigmoid(x)
x = self.fc2(x)
if label is not None:
acc = paddle.metric.accuracy(input=x, label=label)
return x, acc
else:
return x
**对比本章最初定义的LeNet,发现两个LeNet的第一层全连接层的输入特征维度不同,一个是120,一个是30000。**这个不同是输入数据的形状不同引起的,手写字符识别的图像输入形状比较小,第三层卷积之前的特征维度是[B, 120x1x1],但是PALM数据的输入数据形状较大,形状为[B, 120x50x50],120x50x50等于300000,所以不同的输入大小,会影响卷积后全连接层的形状。
# 创建模型
model = LeNet(num_classes=1)
# 启动训练过程
opt = paddle.optimizer.Momentum(learning_rate=0.001, momentum=0.9, parameters=model.parameters())
train_pm(model, optimizer=opt)
evaluation(model, params_file_path="palm.pdparams")
start training ...
epoch: 0, batch_id: 0, loss is: 0.7090
epoch: 0, batch_id: 20, loss is: 0.6811
[validation] accuracy/loss: 0.5275/0.6917
epoch: 1, batch_id: 0, loss is: 0.6771
epoch: 1, batch_id: 20, loss is: 0.6913
[validation] accuracy/loss: 0.5275/0.6917
epoch: 2, batch_id: 0, loss is: 0.6952
epoch: 2, batch_id: 20, loss is: 0.7442
[validation] accuracy/loss: 0.5275/0.6918
epoch: 3, batch_id: 0, loss is: 0.6938
epoch: 3, batch_id: 20, loss is: 0.7144
[validation] accuracy/loss: 0.5275/0.6916
epoch: 4, batch_id: 0, loss is: 0.6509
epoch: 4, batch_id: 20, loss is: 0.6125
[validation] accuracy/loss: 0.5275/0.6923
start evaluation .......
loss=0.6921, acc=0.4675
通过运行结果可以看出,在眼疾筛查数据集iChallenge-PM上,LeNet的loss很难下降,模型没有收敛。这是因为MNIST数据集的图片尺寸比较小( 28 × 28 28\times28 28×28),但是眼疾筛查数据集图片尺寸比较大(原始图片尺寸约为 2000 × 2000 2000 \times 2000 2000×2000,经过缩放之后变成 224 × 224 224 \times 224 224×224),LeNet模型很难进行有效分类。这说明在图片尺寸比较大时,LeNet在图像分类任务上存在局限性。
AlexNet(大图像)
通过上面的实际训练可以看到,虽然LeNet在手写数字识别数据集上取得了很好的结果,但在更大的数据集上表现却并不好。自从1998年LeNet问世以来,接下来十几年的时间里,神经网络并没有在计算机视觉领域取得很好的结果,反而一度被其它算法所超越。原因主要有两方面,一是神经网络的计算比较复杂,对当时计算机的算力来说,训练神经网络是件非常耗时的事情;另一方面,当时还没有专门针对神经网络做算法和训练技巧的优化,神经网络的收敛是件非常困难的事情。
随着技术的进步和发展,计算机的算力越来越强大,尤其是在GPU并行计算能力的推动下,复杂神经网络的计算也变得更加容易实施。另一方面,互联网上涌现出越来越多的数据,极大的丰富了数据库。同时也有越来越多的研究人员开始专门针对神经网络做算法和模型的优化,Alex Krizhevsky等人提出的AlexNet以很大优势获得了2012年ImageNet比赛的冠军。这一成果极大的激发了产业界对神经网络的兴趣,开创了使用深度神经网络解决图像问题的途径,随后也在这一领域涌现出越来越多的优秀成果。
AlexNet与LeNet相比,具有更深的网络结构,包含5层卷积和3层全连接,同时使用了如下三种方法改进模型的训练过程:
-
数据增广:深度学习中常用的一种处理方式,通过对训练随机加一些变化,比如平移、缩放、裁剪、旋转、翻转或者增减亮度等,产生一系列跟原始图片相似但又不完全相同的样本,从而扩大训练数据集。通过这种方式,可以随机改变训练样本,避免模型过度依赖于某些属性,能从一定程度上抑制过拟合。
-
使用Dropout抑制过拟合。
-
使用ReLU激活函数减少梯度消失现象。
说明:
下一节详细介绍数据增广的具体实现方式。
AlexNet的具体结构如 图2 所示:
图2:AlexNet模型网络结构示意图
AlexNet在眼疾筛查数据集iChallenge-PM上具体实现的代码如下所示:
# -*- coding:utf-8 -*-
# 导入需要的包
import paddle
import numpy as np
from paddle.nn import Conv2D, MaxPool2D, Linear, Dropout
## 组网
import paddle.nn.functional as F
# 定义 AlexNet 网络结构
class AlexNet(paddle.nn.Layer):
def __init__(self, num_classes=1):
super(AlexNet, self).__init__()
# AlexNet与LeNet一样也会同时使用卷积和池化层提取图像特征
# 与LeNet不同的是激活函数换成了‘relu’
self.conv1 = Conv2D(in_channels=3, out_channels=96, kernel_size=11, stride=4, padding=5)
self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)
self.conv2 = Conv2D(in_channels=96, out_channels=256, kernel_size=5, stride=1, padding=2)
self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)
self.conv3 = Conv2D(in_channels=256, out_channels=384, kernel_size=3, stride=1, padding=1)
self.conv4 = Conv2D(in_channels=384, out_channels=384, kernel_size=3, stride=1, padding=1)
self.conv5 = Conv2D(in_channels=384, out_channels=256, kernel_size=3, stride=1, padding=1)
self.max_pool5 = MaxPool2D(kernel_size=2, stride=2)
self.fc1 = Linear(in_features=12544, out_features=4096)
self.drop_ratio1 = 0.5
self.drop1 = Dropout(self.drop_ratio1)
self.fc2 = Linear(in_features=4096, out_features=4096)
self.drop_ratio2 = 0.5
self.drop2 = Dropout(self.drop_ratio2)
self.fc3 = Linear(in_features=4096, out_features=num_classes)
def forward(self, x):
x = self.conv1(x)
x = F.relu(x)
x = self.max_pool1(x)
x = self.conv2(x)
x = F.relu(x)
x = self.max_pool2(x)
x = self.conv3(x)
x = F.relu(x)
x = self.conv4(x)
x = F.relu(x)
x = self.conv5(x)
x = F.relu(x)
x = self.max_pool5(x)
x = paddle.reshape(x, [x.shape[0], -1])
x = self.fc1(x)
x = F.relu(x)
# 在全连接之后使用dropout抑制过拟合
x = self.drop1(x)
x = self.fc2(x)
x = F.relu(x)
# 在全连接之后使用dropout抑制过拟合
x = self.drop2(x)
x = self.fc3(x)
return x
# 创建模型
model = AlexNet()
# 启动训练过程
opt = paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters())
train_pm(model, optimizer=opt)
start training ...
epoch: 0, batch_id: 0, loss is: 1.0760
epoch: 0, batch_id: 20, loss is: 0.6632
[validation] accuracy/loss: 0.7500/0.6040
epoch: 1, batch_id: 0, loss is: 0.4665
epoch: 1, batch_id: 20, loss is: 0.7852
[validation] accuracy/loss: 0.9200/0.2427
epoch: 2, batch_id: 0, loss is: 0.5441
epoch: 2, batch_id: 20, loss is: 0.0318
[validation] accuracy/loss: 0.9225/0.2153
epoch: 3, batch_id: 0, loss is: 0.5850
epoch: 3, batch_id: 20, loss is: 0.4100
[validation] accuracy/loss: 0.9150/0.3211
epoch: 4, batch_id: 0, loss is: 0.0401
epoch: 4, batch_id: 20, loss is: 0.0620
[validation] accuracy/loss: 0.9125/0.2570
通过运行结果可以发现,在眼疾筛查数据集iChallenge-PM上使用AlexNet,loss能有效下降,经过5个epoch的训练,在验证集上的准确率可以达到94%左右。
VGG(深度)
VGG是当前最流行的CNN模型之一,2014年由Simonyan和Zisserman提出,其命名来源于论文作者所在的实验室Visual Geometry Group。AlexNet模型通过构造多层网络,取得了较好的效果,但是并没有给出深度神经网络设计的方向。VGG通过使用一系列大小为3x3的小尺寸卷积核和池化层构造深度卷积神经网络,并取得了较好的效果。VGG模型因为结构简单、应用性极强而广受研究者欢迎,尤其是它的网络结构设计方法,为构建深度神经网络提供了方向。
图3 是VGG-16的网络结构示意图,有13层卷积和3层全连接层。VGG网络的设计严格使用 3 × 3 3\times 3 3×3的卷积层和池化层来提取特征,并在网络的最后面使用三层全连接层,将最后一层全连接层的输出作为分类的预测。
**在VGG中每层卷积将使用ReLU作为激活函数,在全连接层之后添加dropout来抑制过拟合。使用小的卷积核能够有效地减少参数的个数,使得训练和测试变得更加有效。**比如使用两层 3 × 3 3\times 3 3×3卷积层,可以得到感受野为5的特征图,而比使用 5 × 5 5 \times 5 5×5的卷积层需要更少的参数。由于卷积核比较小,可以堆叠更多的卷积层,加深网络的深度,这对于图像分类任务来说是有利的。VGG模型的成功证明了增加网络的深度,可以更好的学习图像中的特征模式。

图3:VGG模型网络结构示意图
VGG在眼疾识别数据集iChallenge-PM上的具体实现如下代码所示:
# -*- coding:utf-8 -*-
# VGG模型代码
import numpy as np
import paddle
# from paddle.nn import Conv2D, MaxPool2D, BatchNorm, Linear
from paddle.nn import Conv2D, MaxPool2D, BatchNorm2D, Linear
# 定义vgg网络
class VGG(paddle.nn.Layer):
def __init__(self):
super(VGG, self).__init__()
in_channels = [3, 64, 128, 256, 512, 512]
# 定义第一个block,包含两个卷积
self.conv1_1 = Conv2D(in_channels=in_channels[0], out_channels=in_channels[1], kernel_size=3, padding=1, stride=1)
self.conv1_2 = Conv2D(in_channels=in_channels[1], out_channels=in_channels[1], kernel_size=3, padding=1, stride=1)
# 定义第二个block,包含两个卷积
self.conv2_1 = Conv2D(in_channels=in_channels[1], out_channels=in_channels[2], kernel_size=3, padding=1, stride=1)
self.conv2_2 = Conv2D(in_channels=in_channels[2], out_channels=in_channels[2], kernel_size=3, padding=1, stride=1)
# 定义第三个block,包含三个卷积
self.conv3_1 = Conv2D(in_channels=in_channels[2], out_channels=in_channels[3], kernel_size=3, padding=1, stride=1)
self.conv3_2 = Conv2D(in_channels=in_channels[3], out_channels=in_channels[3], kernel_size=3, padding=1, stride=1)
self.conv3_3 = Conv2D(in_channels=in_channels[3], out_channels=in_channels[3], kernel_size=3, padding=1, stride=1)
# 定义第四个block,包含三个卷积
self.conv4_1 = Conv2D(in_channels=in_channels[3], out_channels=in_channels[4], kernel_size=3, padding=1, stride=1)
self.conv4_2 = Conv2D(in_channels=in_channels[4], out_channels=in_channels[4], kernel_size=3, padding=1, stride=1)
self.conv4_3 = Conv2D(in_channels=in_channels[4], out_channels=in_channels[4], kernel_size=3, padding=1, stride=1)
# 定义第五个block,包含三个卷积
self.conv5_1 = Conv2D(in_channels=in_channels[4], out_channels=in_channels[5], kernel_size=3, padding=1, stride=1)
self.conv5_2 = Conv2D(in_channels=in_channels[5], out_channels=in_channels[5], kernel_size=3, padding=1, stride=1)
self.conv5_3 = Conv2D(in_channels=in_channels[5], out_channels=in_channels[5], kernel_size=3, padding=1, stride=1)
# 使用Sequential 将全连接层和relu组成一个线性结构(fc + relu)
# 当输入为224x224时,经过五个卷积块和池化层后,特征维度变为[512x7x7]
self.fc1 = paddle.nn.Sequential(paddle.nn.Linear(512 * 7 * 7, 4096), paddle.nn.ReLU())
self.drop1_ratio = 0.5
self.dropout1 = paddle.nn.Dropout(self.drop1_ratio, mode='upscale_in_train')
# 使用Sequential 将全连接层和relu组成一个线性结构(fc + relu)
self.fc2 = paddle.nn.Sequential(paddle.nn.Linear(4096, 4096), paddle.nn.ReLU())
self.drop2_ratio = 0.5
self.dropout2 = paddle.nn.Dropout(self.drop2_ratio, mode='upscale_in_train')
self.fc3 = paddle.nn.Linear(4096, 1)
self.relu = paddle.nn.ReLU()
self.pool = MaxPool2D(stride=2, kernel_size=2)
def forward(self, x):
x = self.relu(self.conv1_1(x))
x = self.relu(self.conv1_2(x))
x = self.pool(x)
x = self.relu(self.conv2_1(x))
x = self.relu(self.conv2_2(x))
x = self.pool(x)
x = self.relu(self.conv3_1(x))
x = self.relu(self.conv3_2(x))
x = self.relu(self.conv3_3(x))
x = self.pool(x)
x = self.relu(self.conv4_1(x))
x = self.relu(self.conv4_2(x))
x = self.relu(self.conv4_3(x))
x = self.pool(x)
x = self.relu(self.conv5_1(x))
x = self.relu(self.conv5_2(x))
x = self.relu(self.conv5_3(x))
x = self.pool(x)
x = paddle.flatten(x, 1, -1)
x = self.dropout1(self.relu(self.fc1(x)))
x = self.dropout2(self.relu(self.fc2(x)))
x = self.fc3(x)
return x
# 创建模型
model = VGG()
# opt = paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters())
opt = paddle.optimizer.Momentum(learning_rate=0.001, momentum=0.9, parameters=model.parameters())
# 启动训练过程
train_pm(model, opt)
start training ...
epoch: 0, batch_id: 0, loss is: 1.8103
epoch: 0, batch_id: 20, loss is: 0.4915
[validation] accuracy/loss: 0.9125/0.2522
epoch: 1, batch_id: 0, loss is: 0.4258
epoch: 1, batch_id: 20, loss is: 0.7584
[validation] accuracy/loss: 0.9250/0.2216
epoch: 2, batch_id: 0, loss is: 0.2460
epoch: 2, batch_id: 20, loss is: 0.6798
[validation] accuracy/loss: 0.9475/0.2030
epoch: 3, batch_id: 0, loss is: 0.1671
epoch: 3, batch_id: 20, loss is: 0.1788
[validation] accuracy/loss: 0.9325/0.2176
epoch: 4, batch_id: 0, loss is: 0.1720
epoch: 4, batch_id: 20, loss is: 0.3922
[validation] accuracy/loss: 0.9275/0.1792
通过运行结果可以发现,在眼疾筛查数据集iChallenge-PM上使用VGG,loss能有效的下降,经过5个epoch的训练,在验证集上的准确率可以达到94%左右。
GoogLeNet(深度兼广度)
**GoogLeNet是2014年ImageNet比赛的冠军,它的主要特点是网络不仅有深度,还在横向上具有“宽度”。**由于图像信息在空间尺寸上的巨大差异,如何选择合适的卷积核来提取特征就显得比较困难了。空间分布范围更广的图像信息适合用较大的卷积核来提取其特征;而空间分布范围较小的图像信息则适合用较小的卷积核来提取其特征。为了解决这个问题,GoogLeNet提出了一种被称为Inception模块的方案。如 图4 所示:
说明:
- Google的研究人员为了向LeNet致敬,特地将模型命名为GoogLeNet。
- Inception一词来源于电影《盗梦空间》(Inception)。
图4:Inception模块结构示意图
**图4(a)是Inception模块的设计思想,使用3个不同大小的卷积核对输入图片进行卷积操作,并附加最大池化,将这4个操作的输出沿着通道这一维度进行拼接,构成的输出特征图将会包含经过不同大小的卷积核提取出来的特征,从而达到捕捉不同尺度信息的效果。Inception模块采用多通路(multi-path)的设计形式,每个支路使用不同大小的卷积核,最终输出特征图的通道数是每个支路输出通道数的总和,这将会导致输出通道数变得很大,尤其是使用多个Inception模块串联操作的时候,模型参数量会变得非常大。为了减小参数量,Inception模块使用了图(b)中的设计方式,在每个3x3和5x5的卷积层之前,增加1x1的卷积层来控制输出通道数;在最大池化层后面增加1x1卷积层减小输出通道数。**基于这一设计思想,形成了上图(b)中所示的结构。下面这段程序是Inception块的具体实现方式,可以对照图(b)和代码一起阅读。
提示:
可能有读者会问,经过3x3的最大池化之后图像尺寸不会减小吗,为什么还能跟另外3个卷积输出的特征图进行拼接?这是因为池化操作可以指定窗口大小 k h = k w = 3 k_h = k_w = 3 kh=kw=3,stride=1和padding=1,输出特征图尺寸可以保持不变。
Inception模块的具体实现如下代码所示:
# GoogLeNet模型代码
import numpy as np
import paddle
from paddle.nn import Conv2D, MaxPool2D, AdaptiveAvgPool2D, Linear
## 组网
import paddle.nn.functional as F
# 定义Inception块
class Inception(paddle.nn.Layer):
def __init__(self, c0, c1, c2, c3, c4, **kwargs):
'''
Inception模块的实现代码,
c1,图(b)中第一条支路1x1卷积的输出通道数,数据类型是整数
c2,图(b)中第二条支路卷积的输出通道数,数据类型是tuple或list,
其中c2[0]是1x1卷积的输出通道数,c2[1]是3x3
c3,图(b)中第三条支路卷积的输出通道数,数据类型是tuple或list,
其中c3[0]是1x1卷积的输出通道数,c3[1]是3x3
c4,图(b)中第一条支路1x1卷积的输出通道数,数据类型是整数
'''
super(Inception, self).__init__()
# 依次创建Inception块每条支路上使用到的操作
self.p1_1 = Conv2D(in_channels=c0,out_channels=c1, kernel_size=1)
self.p2_1 = Conv2D(in_channels=c0,out_channels=c2[0], kernel_size=1)
self.p2_2 = Conv2D(in_channels=c2[0],out_channels=c2[1], kernel_size=3, padding=1)
self.p3_1 = Conv2D(in_channels=c0,out_channels=c3[0], kernel_size=1)
self.p3_2 = Conv2D(in_channels=c3[0],out_channels=c3[1], kernel_size=5, padding=2)
self.p4_1 = MaxPool2D(kernel_size=3, stride=1, padding=1)
self.p4_2 = Conv2D(in_channels=c0,out_channels=c4, kernel_size=1)
def forward(self, x):
# 支路1只包含一个1x1卷积
p1 = F.relu(self.p1_1(x))
# 支路2包含 1x1卷积 + 3x3卷积
p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
# 支路3包含 1x1卷积 + 5x5卷积
p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
# 支路4包含 最大池化和1x1卷积
p4 = F.relu(self.p4_2(self.p4_1(x)))
# 将每个支路的输出特征图拼接在一起作为最终的输出结果
return paddle.concat([p1, p2, p3, p4], axis=1)
GoogLeNet的架构如 图5 所示,在主体卷积部分中使用5个模块(block),每个模块之间使用步幅为2的3 ×3最大池化层来减小输出高宽。
- 第一模块使用一个64通道的7 × 7卷积层。
- 第二模块使用2个卷积层:首先是64通道的1 × 1卷积层,然后是将通道增大3倍的3 × 3卷积层。
- 第三模块串联2个完整的Inception块。
- 第四模块串联了5个Inception块。
- 第五模块串联了2 个Inception块。
- 第五模块的后面紧跟输出层,使用全局平均池化层来将每个通道的高和宽变成1,最后接上一个输出个数为标签类别数的全连接层。
说明:
在原作者的论文中添加了图中所示的softmax1和softmax2两个辅助分类器,如下图所示,训练时将三个分类器的损失函数进行加权求和,以缓解梯度消失现象。这里的程序作了简化,没有加入辅助分类器。
图5:GoogLeNet模型网络结构示意图
GoogLeNet的具体实现如下代码所示:
# GoogLeNet模型代码
import numpy as np
import paddle
from paddle.nn import Conv2D, MaxPool2D, AdaptiveAvgPool2D, Linear
## 组网
import paddle.nn.functional as F
# 定义Inception块
class Inception(paddle.nn.Layer):
def __init__(self, c0, c1, c2, c3, c4, **kwargs):
super(Inception, self).__init__()
# 依次创建Inception块每条支路上使用到的操作
self.p1_1 = Conv2D(in_channels=c0,out_channels=c1, kernel_size=1, stride=1)
self.p2_1 = Conv2D(in_channels=c0,out_channels=c2[0], kernel_size=1, stride=1)
self.p2_2 = Conv2D(in_channels=c2[0],out_channels=c2[1], kernel_size=3, padding=1, stride=1)
self.p3_1 = Conv2D(in_channels=c0,out_channels=c3[0], kernel_size=1, stride=1)
self.p3_2 = Conv2D(in_channels=c3[0],out_channels=c3[1], kernel_size=5, padding=2, stride=1)
self.p4_1 = MaxPool2D(kernel_size=3, stride=1, padding=1)
self.p4_2 = Conv2D(in_channels=c0,out_channels=c4, kernel_size=1, stride=1)
# # 新加一层batchnorm稳定收敛
# self.batchnorm = paddle.nn.BatchNorm2D(c1+c2[1]+c3[1]+c4)
def forward(self, x):
# 支路1只包含一个1x1卷积
p1 = F.relu(self.p1_1(x))
# 支路2包含 1x1卷积 + 3x3卷积
p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
# 支路3包含 1x1卷积 + 5x5卷积
p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
# 支路4包含 最大池化和1x1卷积
p4 = F.relu(self.p4_2(self.p4_1(x)))
# 将每个支路的输出特征图拼接在一起作为最终的输出结果
return paddle.concat([p1, p2, p3, p4], axis=1)
# return self.batchnorm()
class GoogLeNet(paddle.nn.Layer):
def __init__(self):
super(GoogLeNet, self).__init__()
# GoogLeNet包含五个模块,每个模块后面紧跟一个池化层
# 第一个模块包含1个卷积层
self.conv1 = Conv2D(in_channels=3,out_channels=64, kernel_size=7, padding=3, stride=1)
# 3x3最大池化
self.pool1 = MaxPool2D(kernel_size=3, stride=2, padding=1)
# 第二个模块包含2个卷积层
self.conv2_1 = Conv2D(in_channels=64,out_channels=64, kernel_size=1, stride=1)
self.conv2_2 = Conv2D(in_channels=64,out_channels=192, kernel_size=3, padding=1, stride=1)
# 3x3最大池化
self.pool2 = MaxPool2D(kernel_size=3, stride=2, padding=1)
# 第三个模块包含2个Inception块
self.block3_1 = Inception(192, 64, (96, 128), (16, 32), 32)
self.block3_2 = Inception(256, 128, (128, 192), (32, 96), 64)
# 3x3最大池化
self.pool3 = MaxPool2D(kernel_size=3, stride=2, padding=1)
# 第四个模块包含5个Inception块
self.block4_1 = Inception(480, 192, (96, 208), (16, 48), 64)
self.block4_2 = Inception(512, 160, (112, 224), (24, 64), 64)
self.block4_3 = Inception(512, 128, (128, 256), (24, 64), 64)
self.block4_4 = Inception(512, 112, (144, 288), (32, 64), 64)
self.block4_5 = Inception(528, 256, (160, 320), (32, 128), 128)
# 3x3最大池化
self.pool4 = MaxPool2D(kernel_size=3, stride=2, padding=1)
# 第五个模块包含2个Inception块
self.block5_1 = Inception(832, 256, (160, 320), (32, 128), 128)
self.block5_2 = Inception(832, 384, (192, 384), (48, 128), 128)
# 全局池化,用的是global_pooling,不需要设置pool_stride
self.pool5 = AdaptiveAvgPool2D(output_size=1)
self.fc = Linear(in_features=1024, out_features=1)
def forward(self, x):
x = self.pool1(F.relu(self.conv1(x)))
x = self.pool2(F.relu(self.conv2_2(F.relu(self.conv2_1(x)))))
x = self.pool3(self.block3_2(self.block3_1(x)))
x = self.block4_3(self.block4_2(self.block4_1(x)))
x = self.pool4(self.block4_5(self.block4_4(x)))
x = self.pool5(self.block5_2(self.block5_1(x)))
x = paddle.reshape(x, [x.shape[0], -1])
x = self.fc(x)
return x
# 创建模型
model = GoogLeNet()
print(len(model.parameters()))
opt = paddle.optimizer.Momentum(learning_rate=0.001, momentum=0.9, parameters=model.parameters(), weight_decay=0.001)
# 启动训练过程
train_pm(model, opt)
116
start training ...
epoch: 0, batch_id: 0, loss is: 0.9782
epoch: 0, batch_id: 20, loss is: 0.6759
[validation] accuracy/loss: 0.8650/0.5639
epoch: 1, batch_id: 0, loss is: 0.5216
epoch: 1, batch_id: 20, loss is: 0.8567
[validation] accuracy/loss: 0.7950/0.5170
epoch: 2, batch_id: 0, loss is: 0.5647
epoch: 2, batch_id: 20, loss is: 0.5026
[validation] accuracy/loss: 0.9000/0.2836
epoch: 3, batch_id: 0, loss is: 0.3838
epoch: 3, batch_id: 20, loss is: 0.3546
[validation] accuracy/loss: 0.9500/0.2316
epoch: 4, batch_id: 0, loss is: 0.2640
epoch: 4, batch_id: 20, loss is: 0.4684
[validation] accuracy/loss: 0.9425/0.1538
通过运行结果可以发现,使用GoogLeNet在眼疾筛查数据集iChallenge-PM上,loss能有效的下降,经过5个epoch的训练,在验证集上的准确率可以达到95%左右。
ResNet
ResNet是2015年ImageNet比赛的冠军,将识别错误率降低到了3.6%,这个结果甚至超出了正常人眼识别的精度。
通过前面几个经典模型学习,我们可以发现随着深度学习的不断发展,模型的层数越来越多,网络结构也越来越复杂。那么是否加深网络结构,就一定会得到更好的效果呢?从理论上来说,假设新增加的层都是恒等映射,只要原有的层学出跟原模型一样的参数,那么深模型结构就能达到原模型结构的效果。换句话说,原模型的解只是新模型的解的子空间,在新模型解的空间里应该能找到比原模型解对应的子空间更好的结果。但是实践表明,增加网络的层数之后,训练误差往往不降反升。
Kaiming He等人提出了残差网络ResNet来解决上述问题,其基本思想如 图6所示。
- 图6(a):表示增加网络的时候,将 x x x映射成 y = F ( x ) y=F(x) y=F(x)输出。
- 图6(b):对图6(a)作了改进,输出 y = F ( x ) + x y=F(x) + x y=F(x)+x。这时不是直接学习输出特征 y y y的表示,而是学习 y − x y-x y−x。
- 如果想学习出原模型的表示,只需将 F ( x ) F(x) F(x)的参数全部设置为0,则 y = x y=x y=x是恒等映射。
- F ( x ) = y − x F(x) = y - x F(x)=y−x也叫做残差项,如果 x → y x\rightarrow y x→y的映射接近恒等映射,图6(b)中通过学习残差项也比图6(a)学习完整映射形式更加容易。
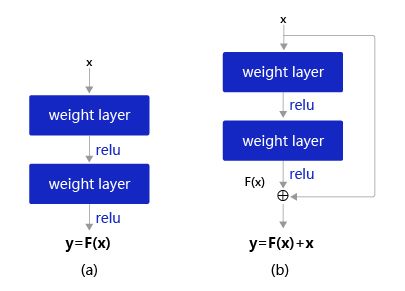
图6:残差块设计思想
图6(b)的结构是残差网络的基础,这种结构也叫做残差块(Residual block)。输入 x x x通过跨层连接,能更快的向前传播数据,或者向后传播梯度。通俗的比喻,在火热的电视节目《王牌对王牌》上有一个“传声筒”的游戏,排在队首的嘉宾把看到的影视片段表演给后面一个嘉宾看,经过四五个嘉宾后,最后一个嘉宾如果能表演出更多原剧的内容,就能取得高分。我们常常会发现刚开始的嘉宾往往表演出最多的信息(类似于Loss),而随着表演的传递,有效的表演信息越来越少(类似于梯度弥散)。如果每个嘉宾都能看到原始的影视片段,那么相信传声筒的效果会好很多。类似的,由于ResNet每层都存在直连的旁路,相当于每一层都和最终的损失有“直接对话”的机会,自然可以更好的解决梯度弥散的问题。残差块的具体设计方案如 图7 所示,这种设计方案也常称作瓶颈结构(BottleNeck)。1*1的卷积核可以非常方便的调整中间层的通道数,在进入3*3的卷积层之前减少通道数(256->64),经过该卷积层后再恢复通道数(64->256),可以显著减少网络的参数量。这个结构(256->64->256)像一个中间细,两头粗的瓶颈,所以被称为“BottleNeck”。
图7:残差块结构示意图
下图表示出了ResNet-50的结构,一共包含49层卷积和1层全连接,所以被称为ResNet-50。

图8:ResNet-50模型网络结构示意图
ResNet-50的具体实现如下代码所示:
# ResNet模型代码
import numpy as np
import paddle
import paddle.nn as nn
import paddle.nn.functional as F
# ResNet中使用了BatchNorm层,在卷积层的后面加上BatchNorm以提升数值稳定性
# 定义卷积批归一化块
class ConvBNLayer(paddle.nn.Layer):
def __init__(self,
num_channels,
num_filters,
filter_size,
stride=1,
groups=1,
act=None):
"""
num_channels, 卷积层的输入通道数
num_filters, 卷积层的输出通道数
stride, 卷积层的步幅
groups, 分组卷积的组数,默认groups=1不使用分组卷积
"""
super(ConvBNLayer, self).__init__()
# 创建卷积层
self._conv = nn.Conv2D(
in_channels=num_channels,
out_channels=num_filters,
kernel_size=filter_size,
stride=stride,
padding=(filter_size - 1) // 2,
groups=groups,
bias_attr=False)
# 创建BatchNorm层
self._batch_norm = paddle.nn.BatchNorm2D(num_filters)
self.act = act
def forward(self, inputs):
y = self._conv(inputs)
y = self._batch_norm(y)
if self.act == 'leaky':
y = F.leaky_relu(x=y, negative_slope=0.1)
elif self.act == 'relu':
y = F.relu(x=y)
return y
# 定义残差块
# 每个残差块会对输入图片做三次卷积,然后跟输入图片进行短接
# 如果残差块中第三次卷积输出特征图的形状与输入不一致,则对输入图片做1x1卷积,将其输出形状调整成一致
class BottleneckBlock(paddle.nn.Layer):
def __init__(self,
num_channels,
num_filters,
stride,
shortcut=True):
super(BottleneckBlock, self).__init__()
# 创建第一个卷积层 1x1
self.conv0 = ConvBNLayer(
num_channels=num_channels,
num_filters=num_filters,
filter_size=1,
act='relu')
# 创建第二个卷积层 3x3
self.conv1 = ConvBNLayer(
num_channels=num_filters,
num_filters=num_filters,
filter_size=3,
stride=stride,
act='relu')
# 创建第三个卷积 1x1,但输出通道数乘以4
self.conv2 = ConvBNLayer(
num_channels=num_filters,
num_filters=num_filters * 4,
filter_size=1,
act=None)
# 如果conv2的输出跟此残差块的输入数据形状一致,则shortcut=True
# 否则shortcut = False,添加1个1x1的卷积作用在输入数据上,使其形状变成跟conv2一致
if not shortcut:
self.short = ConvBNLayer(
num_channels=num_channels,
num_filters=num_filters * 4,
filter_size=1,
stride=stride)
self.shortcut = shortcut
self._num_channels_out = num_filters * 4
def forward(self, inputs):
y = self.conv0(inputs)
conv1 = self.conv1(y)
conv2 = self.conv2(conv1)
# 如果shortcut=True,直接将inputs跟conv2的输出相加
# 否则需要对inputs进行一次卷积,将形状调整成跟conv2输出一致
if self.shortcut:
short = inputs
else:
short = self.short(inputs)
y = paddle.add(x=short, y=conv2)
y = F.relu(y)
return y
# 定义ResNet模型
class ResNet(paddle.nn.Layer):
def __init__(self, layers=50, class_dim=1):
"""
layers, 网络层数,可以是50, 101或者152
class_dim,分类标签的类别数
"""
super(ResNet, self).__init__()
self.layers = layers
supported_layers = [50, 101, 152]
assert layers in supported_layers, \
"supported layers are {} but input layer is {}".format(supported_layers, layers)
if layers == 50:
#ResNet50包含多个模块,其中第2到第5个模块分别包含3、4、6、3个残差块
depth = [3, 4, 6, 3]
elif layers == 101:
#ResNet101包含多个模块,其中第2到第5个模块分别包含3、4、23、3个残差块
depth = [3, 4, 23, 3]
elif layers == 152:
#ResNet152包含多个模块,其中第2到第5个模块分别包含3、8、36、3个残差块
depth = [3, 8, 36, 3]
# 残差块中使用到的卷积的输出通道数
num_filters = [64, 128, 256, 512]
# ResNet的第一个模块,包含1个7x7卷积,后面跟着1个最大池化层
self.conv = ConvBNLayer(
num_channels=3,
num_filters=64,
filter_size=7,
stride=2,
act='relu')
self.pool2d_max = nn.MaxPool2D(
kernel_size=3,
stride=2,
padding=1)
# ResNet的第二到第五个模块c2、c3、c4、c5
self.bottleneck_block_list = []
num_channels = 64
for block in range(len(depth)):
shortcut = False
for i in range(depth[block]):
# c3、c4、c5将会在第一个残差块使用stride=2;其余所有残差块stride=1
bottleneck_block = self.add_sublayer(
'bb_%d_%d' % (block, i),
BottleneckBlock(
num_channels=num_channels,
num_filters=num_filters[block],
stride=2 if i == 0 and block != 0 else 1,
shortcut=shortcut))
num_channels = bottleneck_block._num_channels_out
self.bottleneck_block_list.append(bottleneck_block)
shortcut = True
# 在c5的输出特征图上使用全局池化
self.pool2d_avg = paddle.nn.AdaptiveAvgPool2D(output_size=1)
# stdv用来作为全连接层随机初始化参数的方差
import math
stdv = 1.0 / math.sqrt(2048 * 1.0)
# 创建全连接层,输出大小为类别数目,经过残差网络的卷积和全局池化后,
# 卷积特征的维度是[B,2048,1,1],故最后一层全连接的输入维度是2048
self.out = nn.Linear(in_features=2048, out_features=class_dim,
weight_attr=paddle.ParamAttr(
initializer=paddle.nn.initializer.Uniform(-stdv, stdv)))
def forward(self, inputs):
y = self.conv(inputs)
y = self.pool2d_max(y)
for bottleneck_block in self.bottleneck_block_list:
y = bottleneck_block(y)
y = self.pool2d_avg(y)
y = paddle.reshape(y, [y.shape[0], -1])
y = self.out(y)
return y
# 创建模型
model = ResNet()
# 定义优化器
opt = paddle.optimizer.Momentum(learning_rate=0.001, momentum=0.9, parameters=model.parameters(), weight_decay=0.001)
# 启动训练过程
train_pm(model, opt)
epoch: 0, batch_id: 0, loss is: 0.7637
epoch: 0, batch_id: 20, loss is: 0.6747
[validation] accuracy/loss: 0.7450/0.5256
epoch: 1, batch_id: 0, loss is: 0.4384
epoch: 1, batch_id: 20, loss is: 0.3936
[validation] accuracy/loss: 0.8475/0.3881
epoch: 2, batch_id: 0, loss is: 0.3581
epoch: 2, batch_id: 20, loss is: 0.3425
[validation] accuracy/loss: 0.9350/0.1978
epoch: 3, batch_id: 0, loss is: 0.9602
epoch: 3, batch_id: 20, loss is: 0.2040
[validation] accuracy/loss: 0.9425/0.1826
epoch: 4, batch_id: 0, loss is: 0.2021
epoch: 4, batch_id: 20, loss is: 0.3348
[validation] accuracy/loss: 0.9350/0.1805
通过运行结果可以发现,使用ResNet在眼疾筛查数据集iChallenge-PM上,loss能有效的下降,经过5个epoch的训练,在验证集上的准确率可以达到96%左右。
使用飞桨高层API直接调用图像分类网络
飞桨开源框架2.0版本支持全新升级的API体系,除了基础API外,还支持了高层API。通过高低融合实现灵活组网,让飞桨API更简洁、更易用、更强大。高层API支持paddle.vision.models接口,实现了对常用模型的封装,包括ResNet、VGG、MobileNet、LeNet等。使用高层API调用这些网络,可以快速完成神经网络的训练和Fine-tune。
代码示例如下:
import paddle
from paddle.vision.models import resnet50
# 调用高层API的resnet50模型
model = resnet50()
# 设置pretrained参数为True,可以加载resnet50在imagenet数据集上的预训练模型
# model = resnet50(pretrained=True)
# 随机生成一个输入
x = paddle.rand([1, 3, 224, 224])
# 得到残差50的计算结果
out = model(x)
# 打印输出的形状,由于resnet50默认的是1000分类
# 所以输出shape是[1x1000]
print(out.shape)
[1, 1000]
使用paddle.vision中的模型可以简单快速的构建一个深度学习任务,如下示例,仅14行代码即可实现resnet在Cifar10数据集上的训练。
# 从paddle.vision.models 模块中import 残差网络,VGG网络,LeNet网络
from paddle.vision.models import resnet50, vgg16, LeNet
from paddle.vision.datasets import Cifar10 # 数据集 Cifar10
from paddle.optimizer import Momentum # 优化算法 Momentum
from paddle.regularizer import L2Decay # 正则化 L2Decay
from paddle.nn import CrossEntropyLoss # 评估算法 CrossEntropyLoss
from paddle.metric import Accuracy # 计算预测准确率 Accuracy
from paddle.vision.transforms import Transpose # 矩阵转置 Transpose
# 确保从paddle.vision.datasets.Cifar10中加载的图像数据是np.ndarray类型
paddle.vision.set_image_backend('cv2')
# 调用 resnet50 模型来;
model = paddle.Model(resnet50(pretrained=False, num_classes=10))
# 使用Cifar10数据集
train_dataset = Cifar10(mode='train', transform=Transpose())
val_dataset = Cifar10(mode='test', transform=Transpose())
# 定义优化器
optimizer = Momentum(learning_rate=0.01,
momentum=0.9,
weight_decay=L2Decay(1e-4),
parameters=model.parameters())
# 进行训练前准备
model.prepare(optimizer, CrossEntropyLoss(), Accuracy(topk=(1, 5)))
# 启动训练
model.fit(train_dataset,
val_dataset,
epochs=50,
batch_size=64,
save_dir="./output",
num_workers=8)
小结
在这一节里,给读者介绍了几种经典的图像分类模型,分别是LeNet, AlexNet, VGG, GoogLeNet和ResNet,并将它们应用到眼疾筛查数据集上。除了LeNet不适合大尺寸的图像分类问题之外,其它几个模型在此数据集上损失函数都能显著下降,在验证集上的预测精度在95%左右。如果读者有兴趣的话,可以进一步调整学习率和训练轮数等超参数,观察是否能够得到更高的精度。除此之外,还介绍了高层API直接调用常用深度神经网络的方法,方便开发者们快速完成深度学习网络迭代。