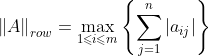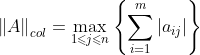矩阵分析与应用

矩阵的范数与内积

实矩阵的范数记作，它是矩阵A的实值函数，必须具有以下性质：

1. 对于任何非零矩阵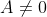，其范数大于零，即，并且。
2. 对于任何复数c有。
3. 矩阵范数满足三角不等式
4. 两个矩阵乘积的范数小于或等于两个矩阵范数的乘积，即。

实函数是一种矩阵范数。

举例：，则有

容易验证：

（1），且当即时。

（2）

（3）

（4）对于两个矩阵的乘积，有：

以下是几种典型的矩阵范数

Frobenius范数

这一定义可以视为向量的Euclidean范数按照矩阵各行排列的“长向量”

的推广。矩阵的Frobenius范数也称Euclidean范数或者范数

举例：,则有

范数

式中，是向量x的范数，范数也称p范数。

行和范数

举例：,则

列和范数

举例：，则

若A，B是m*n的矩阵，则矩阵的范数有以下性质。

与矩阵的范数密切相关的量是矩阵的内积。对于任意m*n的复矩阵A和B，矩阵的内积记作，定义为：

以下是矩阵的内积和范数之间的关系。

1.Cauchy-Schwartz不等式

当且仅当A=cB时（其中c为某个复常数），等号成立。

2.Pathagoras定理

3.极化恒等式

其中Re（）表示取复数的实部。