数字图像处理知识点复习(上)
数字图像处理
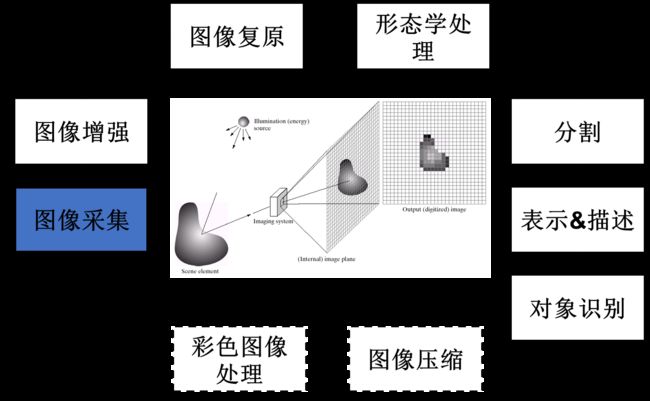
- 绪论(一些基本概念)
-
- 图像(Image)
- 数字图像
- 图像表示
-
- 矩阵表示
- 向量表示
- 数字图像处理
-
- 概念
- 特点
- 目的
- 高级图像编辑
- 数字图像处理基础
-
- 视觉过程
- 采样量化
- 图像类型
-
- 二值图像
- 灰度图像
- 真彩色图像
- 伪彩色图像
- 图像存储(自学)
- 像素间的关系(重点)
-
- 邻域
- 邻接
- 连接
- 像素间的通路
- 像素的连通
- 像素集合间的邻接、连接、连通
- 像素间的距离
授课教师:Yuwei Wu 武玉伟
https://sites.google.com/site/wuyuweibit/
绪论(一些基本概念)
图像(Image)
对物体或场景的一种表现形式。
信息载体
抽象定义: 二 维 函 数 f ( x , y ) ( x , y ) : 点 的 空 间 坐 标 ( 实 数 ) f : 点 ( x , y ) 的 幅 度 ( 亮 度 、 强 度 或 灰 度 ) 二维函数f(x,y) (x,y):点的空间坐标(实数) f:点(x,y)的幅度(亮度、强度或灰度) 二维函数f(x,y)(x,y):点的空间坐标(实数)f:点(x,y)的幅度(亮度、强度或灰度)
数字图像
数 字 化 : 对 x , y 和 f 进 行 离 散 化 , 其 中 每 个 点 称 为 图 像 元 素 , 即 像 素 。 数字化:对x,y和f进行离散化,其中每个点称为图像元素,即像素。 数字化:对x,y和f进行离散化,其中每个点称为图像元素,即像素。
图像表示
矩阵表示
F = ( f 11 f 12 . . . f 1 c f 21 f 22 . . . f 2 c . . . . . . . . . . . . f r 1 f r 2 . . . f r c ) F=\begin{pmatrix} f_{11} & f_{12} & ... &f_{1c} \\ f_{21} & f_{22} & ... &f_{2c} \\ ... & ... & ... & ...\\ f_{r1} & f_{r2} & ... &f_{rc} \end{pmatrix} F=⎝⎜⎜⎛f11f21...fr1f12f22...fr2............f1cf2c...frc⎠⎟⎟⎞

向量表示
F = [ f 1 f 2 . . . f N ] f i = [ f 1 i f 2 i . . . f M i ] T i = 1 , 2 , . . . , N F=[ f_1 f_2 ... f_N] f_i=[f_{1i} f_{2i} ... f_{Mi}]^T i=1,2,...,N F=[f1f2...fN]fi=[f1if2i...fMi]Ti=1,2,...,N

图像表示所用坐标系:
屏幕显示:左上角为原点
图像计算:左下角为原点
数字图像处理
概念
广义:与图像相关的处理
- 图像分析、理解
- 计算机视觉
- …
| 类型 | 输入 | 输出 |
|---|---|---|
| 低层处理 | 图像 | 图像 |
| 中层处理 | 图像分割及图像的描述 | 目标的特征数据 |
| 高层处理 | 目标物体及相互关系的理解 | 更抽象的数据 |
图像处理主要是底层处理及部分中层处理
狭义(从输入输出内容):对图像进行各种加工,以改善图像的视觉效果或突出目标,强调图像之间进行的变换,是一个从图像到图像的过程
特点
- 图像信息量大、数据量也大
- 图像处理技术综合性强
- 图像信息理论与通信理论密切相关
高空间频率波决定图像的细节,低空间频率波决定图像的背景和动态范围。
目的
- 提高图像的视觉质量。
如,去除图像中的噪声,改变图像的亮度、颜色,增强图像中的某些成份、抑制另一些成份,对图像进行几何变换等,从而改善图像的质量,以达到或真实的、或清晰的、或色彩丰富的、或意想不到的视觉效果。 - 提取图像中所包含的某些特征或特殊信息,以便于计算机分析与处理。
这些特征包括很多方面,如频域特性、灰度/颜色特性、边界/区域特性、纹理特性、形状/拓扑特性以及关系结构等 - 对图像数据进行变换、编码和压缩,以便于图像的存储和传输。

高级图像编辑
图像修补
图像重定向
图像重排
图像组合
数字图像处理基础
视觉过程
”视“过程: 图像采集
“觉”过程:图像感知
生物视觉:
晶状体(lens)----相机镜头
瞳孔(pupil)----光圈
视网膜(retina)—胶片
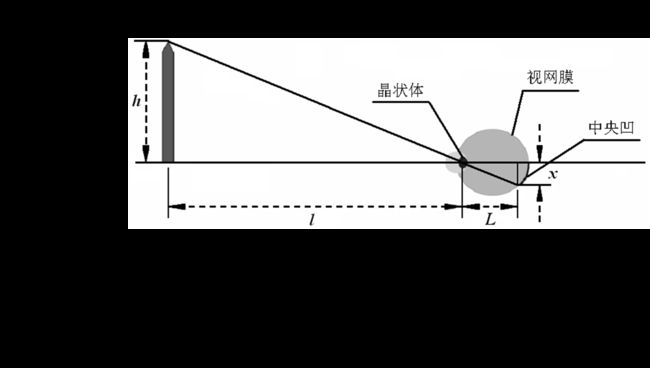
晶状体的屈光能力从最小变到最大时,晶状体聚焦中心和视网膜间的距离可以从约17mm变到约14mm。故L的取值范围为: 14 m m ≤ L ≤ 17 m m 14mm \leq L \leq 17mm 14mm≤L≤17mm
注意:当眼睛聚焦在一个3m以外的物体时,晶状体具有最小的屈光能力,即晶状体聚焦中心和视网膜间的距离为约17mm。当眼睛聚焦在一个3m以内的物体时,晶状体具有最大的屈光能力,即晶状体聚焦中心和视网膜间的距离L约为14mm。
视觉特性:
视觉感知的外在表现,包括视觉对光强,对各种波长、色彩的光谱响应,对物体边缘等空间频率变化的响应,以及视觉对时间瞬时变化运动的响应等
- 亮度对比度: 图 像 中 亮 度 最 大 值 和 最 小 值 的 比 值 C = I m a x I m i n 图像中亮度最大值和最小值的比值 C=\frac{I_{max}}{I_{min}} 图像中亮度最大值和最小值的比值C=IminImax
- 相对对比度: 物 体 亮 度 I T 和 背 景 亮 度 I B 差 值 与 背 景 亮 度 I B 的 比 值 物体亮度I_T和背景亮度I_B差值与背景亮度I_B的比值 物体亮度IT和背景亮度IB差值与背景亮度IB的比值
C = I T − I B I B C=\frac{I_T-I_B}{I_B} C=IBIT−IB
亮度视觉范围:
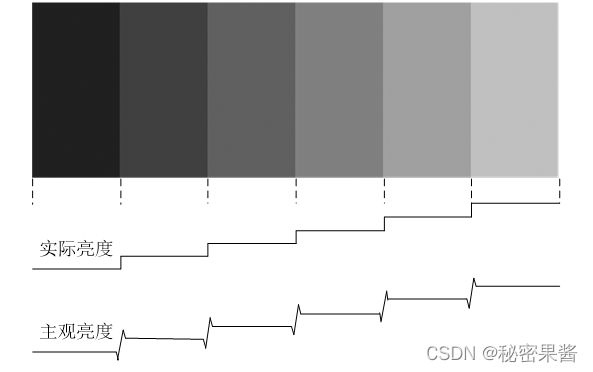
人的视觉系统感受到的物体亮度是主观亮度,亮度视觉范围是人眼能感觉到的亮度范围。 - 同时对比度
大小一样且亮度相同的目标物处于不同的亮度背景中,人眼感受到的主观亮度不同。
采样量化
现实生活:见到的图像一般是连续形式的模拟图像,可由f(x,y)描述
f(x,y)是点(x,y)颜色的深浅
数字图像处理:将连续图像静采样、量化(离散),转换为数字图像
空间采样:空间坐标的离散化----确定图像的空间分辨率
灰度量化:灰度值(颜色深浅幅度)的离散化----确定图像的幅度分辨率
量化过程:给点(x,y)(x,y均取整数)赋予灰度值f,f取整数
数 字 图 像 处 理 中 : 一 幅 图 像 尺 寸 ( 空 间 分 辨 率 为 M ∗ N , 表 明 成 像 时 采 样 M ∗ N 个 , 包 含 M ∗ N 个 像 素 数字图像处理中: 一幅图像尺寸(空间分辨率为M*N,表明成像时采样M*N个,包含M*N个像素 数字图像处理中:一幅图像尺寸(空间分辨率为M∗N,表明成像时采样M∗N个,包含M∗N个像素
如 果 每 个 像 素 都 用 G 个 灰 度 值 中 的 一 个 来 赋 值 , 表 明 成 像 时 量 化 成 了 G 个 灰 度 级 ( 幅 度 分 辨 率 ) 如果每个像素都用G个灰度值中的一个来赋值,表明成像时量化成了G个灰度级(幅度分辨率) 如果每个像素都用G个灰度值中的一个来赋值,表明成像时量化成了G个灰度级(幅度分辨率)
一 般 将 这 些 量 取 为 2 的 整 数 次 幂 图 像 水 平 尺 寸 M : M = 2 m 图 像 垂 直 尺 寸 N : N = 2 n 图 像 灰 度 级 数 L : L = 2 k , 即 k 位 图 像 图 像 所 需 比 特 数 b : b = M ∗ N ∗ k 一般将这些量取为2的整数次幂 \\ 图像水平尺寸M:M=2^m \\ 图像垂直尺寸N: N=2^n \\ 图像灰度级数L:L=2^k ,即k位图像 \\ 图像所需比特数b:b=M*N*k 一般将这些量取为2的整数次幂图像水平尺寸M:M=2m图像垂直尺寸N:N=2n图像灰度级数L:L=2k,即k位图像图像所需比特数b:b=M∗N∗k
图像分辨率和灰度级对图像大小的影响
试求一段采用PAL制式、分辨率为1024×768、长度为1分钟的高清彩色视频所占用的存储空间的大小( PAL制式为25帧/秒,即每秒播放25副24位图像)。
1 分 钟 的 视 频 共 需 存 储 25 × 60 = 1500 副 图 像 ; 由 彩 色 图 像 每 个 像 素 需 要 用 3 个 字 节 ( B y t e ) 存 储 , 因 此 , 一 副 分 辨 率 为 1024 × 768 的 图 像 需 要 占 用 1024 × 768 × 3 ( B y t e s ) = 2359296 ( B y t e s ) = 2303 ( K B y t e s ) = 2.25 ( M B y t e s ) ; 因 此 , 该 段 视 频 所 占 用 的 存 储 空 间 为 : 1500 × 2.25 ( M B y t e s ) = 3375 ( M B y t e s ) = 3.30 ( G B y t e s ) 。 1分钟的视频共需存储25×60=1500副图像;\\由彩色图像每个像素需要用3个字节(Byte)存储,因此,一副分辨率为1024×768的图像需要占用\\1024×768×3(Bytes)=2359296(Bytes)=2303(KBytes)=2.25(MBytes);\\因此,该段视频所占用的存储空间为:\\1500×2.25(MBytes)=3375(MBytes)=3.30(GBytes)。 1分钟的视频共需存储25×60=1500副图像;由彩色图像每个像素需要用3个字节(Byte)存储,因此,一副分辨率为1024×768的图像需要占用1024×768×3(Bytes)=2359296(Bytes)=2303(KBytes)=2.25(MBytes);因此,该段视频所占用的存储空间为:1500×2.25(MBytes)=3375(MBytes)=3.30(GBytes)。
空间分辨率和幅度分辨率的变化对图像质量的影响
空间分辨率减小、幅度分辨率不变时,图像质量由精细变得粗糙。
空间分辨率不变、幅度分辨率减小时,图像质量由精细变得粗糙。
空间分辨率减小、同时幅度分辨率减小时,图像质量由精细变得粗糙,且变化的速度加快。
图像类型
指图像的颜色深度与像素颜色之间的关系
颜色深度:
每一个像素的颜色值所占的二进制位数
例如:颜色深度为8,表示每一个像素的颜色值占8个二进制位,即1个字节
颜色数:每个像素所有可能的颜色值的个数,即图像颜色表的表项数
颜色深度为8的图像的颜色数为28=256。
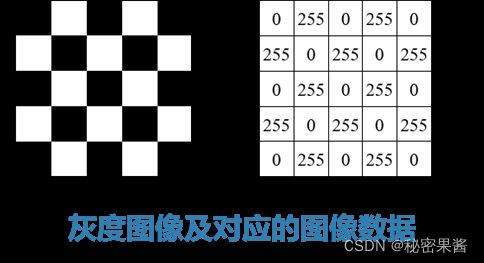
二值图像
也叫单色图像或一位图像,及颜色深度为1的图像
颜色深度为1表示每个像素点仅占1位,一般0表示黑1表示白

灰度图像
包含灰度级(亮度)的图像
特点:
- 灰度图像的存储文件包含图像颜色表,有256项,一项由红、绿、蓝颜色分量组成,且红绿蓝颜色分量的之都相等
f G ( x , y ) = f R ( x , y ) = f B ( x , y ) f_G(x,y)=f_R(x,y)=f_B(x,y) fG(x,y)=fR(x,y)=fB(x,y) - 每个像素由8位组成,值范围0~255,表示256种不同的灰度级
- 像素值f(x,y)是图像颜色表的表项入口地址
真彩色图像
特点:
- 真彩色图像的图像文件中不包含图像颜色表
- 每个像素由R,G,B三个分量组成,每个分量各占8位,每个像素共战24位
- 每个分量取值范围0~255
伪彩色图像
- 特点:
- 存储文件包含图像颜色表,有256项,每一项由红绿蓝颜色分量组成,且分量值不全相等
f G ( x , y ) ≠ f R ( x , y ) ≠ f B ( x , y ) f_G(x,y)\neq f_R(x,y)\neq f_B(x,y) fG(x,y)=fR(x,y)=fB(x,y) - 像素值f(x,y)是图像颜色表的入口地址
图像存储(自学)
数字图像根据其不同特性,可分为两类:点阵图(又称光栅图)和矢量图。
数字图像文件格式有很多种,不同的操作系统和应用软件常使用不同的图像文件格式。
BMP文件格式
JPEG文件格式
TIFF文件格式
GIF文件格式
PNG文件格式
像素间的关系(重点)
邻域
一个像素的邻近像素组成该像素的邻域
- 4 − 邻 域 N 4 ( p ) 4-邻域N_4(p) 4−邻域N4(p)
- 对 角 邻 域 N D ( p ) 对角邻域N_D(p) 对角邻域ND(p)
- 8 邻 域 N 8 ( p ) 8邻域N_8(p) 8邻域N8(p)
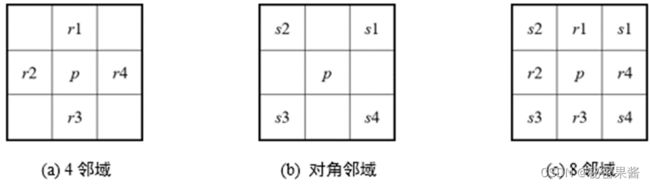
如 果 像 素 p 本 身 在 图 像 边 缘 , 则 它 的 N 4 ( p ) , N D ( p ) 和 N 8 ( p ) 中 的 若 干 个 像 素 降 落 在 图 像 外 如果像素p本身在图像边缘,则它的N_4(p),N_D(p)和N_8(p)中的若干个像素降落在图像外 如果像素p本身在图像边缘,则它的N4(p),ND(p)和N8(p)中的若干个像素降落在图像外
邻接
一个像素与在它邻域中的像素是接触的,称为邻接(adjacency)的。
像素邻接的类型
- 4-邻接
一个像素与在它4-邻域中的像素接触。 - 对角邻接
一个像素与在它对角邻域中的像素接触。 - 8-邻接
一个像素与在它8-邻域中的像素接触。
邻接仅考虑了像素间的空间关系
连接
需要考虑两点:
(1)是否邻接(即是否接触);
(2)灰度值是否满足某个特定的相似准则。
“灰度值”也可以是其它属性值。
“相似准则”可以是灰度值相等,或同在一个灰度值集合中取值。
例如:设V表示定义连接的灰度值集合,则有:
在一幅二值图像中,考虑两个灰度值为1的像素之间的连接,取V={1}。
在一幅有32个灰度级的灰度图中,考虑灰度值在8到15间的两个像素的连接时,取V={8,9,…,15}。
像素连接的类型
- 4-连接
两个像素p和r在V中取值且r在N4(p)中。
r在N4(p)中意味着p也在N4(r)中。 - 8-连接
两个像素p和r在V中取值且r在N8 ( p)中。
r在N8 (p )中意味着p也在N8( r)中。 - m-连接(混合连接)
两个像素p和r在V中取值且满足下列两个条件之一:
(1) r在N4( p)中。即两个像素p和r是4-连接。
(2) r在ND( p)中且N4( p)∩N4(r )在V的意义下是空集。
即N4( p)∩N4( r)不包含V中取值的像素。
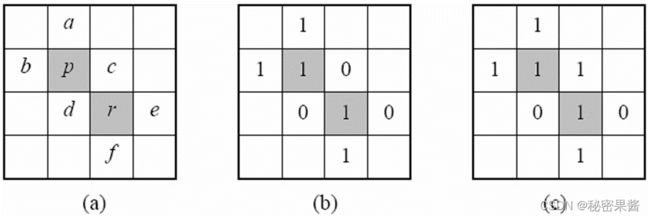
例:混合连接的判定。一副4×4的二值图像模板如(a)所示,相似准则V={1},当图像数据如 (b)和 ©取值时,判定像素p和r是否满足混合连接的条件。
(a):r∈ND§且N4§∩N4®={c,d}。
(b):设V={1},该图满足混合连接条件。 pr像素值均为1,p和r不是4连接,不满足条件一;N4( p)∩N4(r )={0},在V的意义下,N4( p)∩N4(r )=空集,满足条件二
©:设V={1},该图不满足混合连接条件。在V的意义下,N4( p)∩N4(r )={1}
像素间的通路
从具有坐标(x, y)的像素p到具有坐标(s, t)的像素q的一条通路由一系列具有坐标(x0, y0),(x1, y1),…,(xn, yn)的独立像素组成。
(1)(x0, y0) = (x, y),(xn, yn) = (s, t)。
(2)(xi, yi)与(xi-1, yi-1)邻接。
(3)1≤i≤ n,n为通路长度。
根据不同的邻接定义,可以得到不同的通路。
如: 4-邻接=>4-通路,8-邻接=>8-通路。
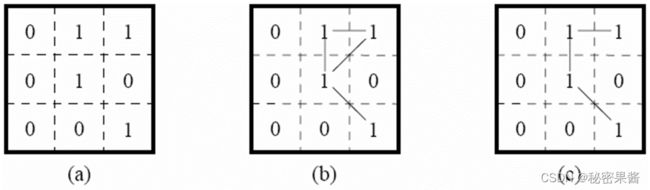
例:多路问题。一副3×3的二值图像模板如图(a)所示,相似准则V={1},像素a、b、c、d的灰度值均取1,像素e的灰度值取0。试分析采用8连接和混合连接时像素a、b、c、d的连接情况。
(a):原始图像。
(b):当V={1}时的8-连接图像。歧义性:中心像素和右上角像素间存在连线。
©:用m-连接消除歧义性后的图像。
中心像素和右上角像素间的m-连接不能成立。
像素的连通
像素间通路上所有像素的灰度值均满足某个特定的相似准则,则像素p和q是连通的。
根据不同的连接定义,可以得到不同的连通。
如:4-连接=>4-连通,8-连接=>8-连通。
连接可以看作是像素连通的一种特例。
两个连通的像素也是连接的,n=1时。
像素集合间的邻接、连接、连通
对两个图像子集 S 和 T 来说,如果S中的一个或一些像素与 T 中的一个或一些像素邻接,则可以说两个图像子集S 和 T 是邻接的。
可以说,两个图像子集是4-邻接、8-邻接的
对两个图像子集 S 和 T 来说,如果S中的一个或一些像素与 T 中的一个或一些像素连接,则可以说两个图像子集S 和 T 是连接的。
设p和q是一个图像子集S中的两个像素,如果存在一条完全由在S中的像素组成的从p到q的通路,则称p在S中与q 连通
对S中任一个像素p,所有与p相连通且又在S中的像素的集合(包括p)合起来称为S中的一个连通组元。
像素间的距离
指像素在空间的接近程度
设3个像素为p、q和r,坐标分别为(x,y)、(s,t)和(u,v),则距离量度函数D必须满足下列三个条件:
(1) D(p,q)≥0
(2) D(p,q)=D(q,p)
(3) D(p,r)≤D(p,q)+D(q,r)
条件(1)表明两个像素之间的距离总是为正值,若D(p,q)=0当且仅当p=q;
条件(2)表明像素之间的距离与起点和终点的选择无关;
条件(3)表明像素之间的最短距离是沿直线的。
常见的距离度量方法包括欧式距离、城区距离、棋盘距离和混合距离。
-
D_E距离即欧氏(Euclidean)距离 是范数为2的距离。
点p和q之间的欧氏距离定义为:
D E ( p , q ) = [ ( x − s ) 2 + ( y − t ) 2 ] 1 2 D_E(p,q)=[(x-s)^2+(y-t)^2]^{\frac{1}{2}} DE(p,q)=[(x−s)2+(y−t)2]21
几何意义
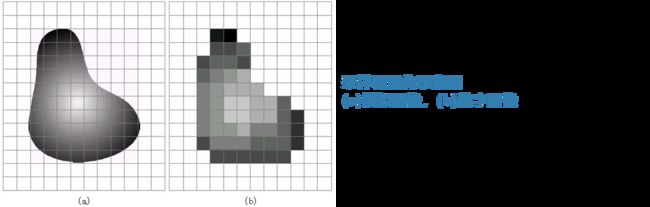
与坐标为(x,y)的像素的DE距离小于或等于某个值d的像素都包括在以**(x,y)为中心以d为半径的圆中**。如(a),对应的3-D透视图如(b) 。
图(a):与(x,y)的DE距离小于或等于3的像素构成的圆形区域。在数字图像中,圆只能近似地表示。图中距离值已四舍五入到保留一位小数。

-
D_4距离即城区(city-block)距离,是范数为1的距离。
点p和q之间的城区距离定义为: D 4 ( p , q ) = ︱ x − s ︱ + ︱ y − t ︱ D_4(p,q)=︱x-s︱+︱y-t︱ D4(p,q)=︱x−s︱+︱y−t︱
几何意义
与坐标为(x,y)的像素的D4距离小于或等于某个值d的像素都包括在以(x,y)为中心的菱形中。如图(a),对应的3-D透视图如图(b) 。
与(x,y)的D4距离小于或等于3的像素构成的菱形区域。D4=1的像素就是(x,y)的4-邻域像素,因此,像素p的4-邻域可以通过城区距离来定义(r表示某个像素。) N 4 ( p ) = r ︱ D 4 ( p , r ) = 1 N_4(p)={r︱D_4(p,r)=1} N4(p)=r︱D4(p,r)=1

-
D_8距离即棋盘(chessboard)距离,是范数为∞的距离。
点p和q之间的棋盘距离定义为: D 8 ( p , q ) = m a x ( ︱ x − s ︱ , ︱ y − t ︱ ) D_8(p,q)=_{max}(︱x-s︱,︱y-t︱) D8(p,q)=max(︱x−s︱,︱y−t︱)
几何意义
与坐标为(x,y)的像素的D8距离小于或等于某个值d的像素都包括在以(x,y)为中心的正方形中。如图(a),对应的3-D透视图如图(b) 。
与(x,y)的D8距离小于或等于3的像素构成的正方形区域。D8=1的像素就是(x,y)的8-邻域像素,因此,像素p的8-邻域可以通过棋盘距离来定义(r表示某个像素。) N 8 ( p ) = r ︱ D 8 ( p , r ) = 1 N_8 (p)={r︱D_8(p,r)=1} N8(p)=r︱D8(p,r)=1

像素点之间的混合距离(Dm)同样刻画了像素在空间的接近程度,其大小不仅与像素的坐标有关,还与像素本身及其邻近像素的属性值有关。两个像素点p和q之间的混合距离Dm (p,q)等于它们之间满足混合连通的通路的长度。
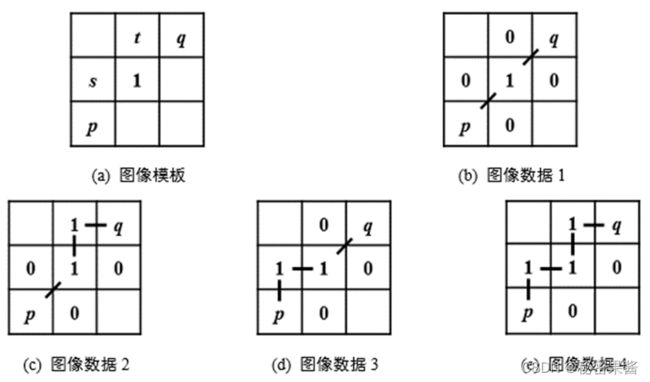
混合距离示例。一副3×3的二值图像模板如图(a)所示,相似准则V={1},像素p和q的灰度值均取1。试求:当像素s和t的灰度值如图(b)、图©、图(d)和图(e)取值时,像素p和q之间的混合距离Dm(p,q)。
先判定是否混合连接
当像素s和t的灰度值如图(b)取值时,满足混合连通的通路如图所示,Dm(p,q)=2。
当像素s和t的灰度值如图©取值时,满足混合连通的通路如图所示,Dm(p,q)=3。
当像素s和t的灰度值如图(d)取值时,满足混合连通的通路如图所示,Dm(p,q)=3。
当像素s和t的灰度值如图(e)取值时,满足混合连通的通路如图所示,Dm(p,q)=4。