波束形成算法：LCMV实现（MATLAB）

---

前言

在这里记录阵列信号处理的学习过程。

---

一、波束形成原理

  利用阵元直接相干叠加而获得输出，其缺点在于只有垂直于阵列平面方向的入射波在阵列输出端才能同相叠加，从而形成方向图中主瓣的极大值。反过来说，如果阵列可以围绕它的中心轴旋转，那么当阵列输出为最大时，空间波必然由垂直于阵列平面的方向入射而来。但有些天线阵列是很庞大的，且是不能转动的。因此，设法设计一种相控阵天线法(或称常规波束形成法)，这是最早出现的阵列信号处理方法。在这种方法中，阵列输出选取一个适当的加权向量以补偿各个阵元的传播延时，从而使在某一期望方向上阵列输出可以同相叠加，进而使阵列在该方向上产生一个主瓣波束，而对其他方向上产生较小的响应，用这种方法对整个空间进行波束扫描就可确定空中待测信号的方位。
  以一维M元等距线阵为例，如下图所示，设空间信号为窄带信号，每个通道用一个复加权系数来调整该通道的幅度和相位。

这时阵列的输出可表示为
$$y(t)=\sum _{i=1}^M{w}_i^{\ast }(\theta )x_i(t)$$
采用向量形式表达，可得到以下公式
$$y(t)=w^H(\theta )x(t)$$
其中，$x(t)=[x_1(t)x_2(t)\dots x_M(t){]}^T,w(\theta )=[w_1(\theta )w_2(\theta )\dots w_M(\theta ){]}^T$

二、波束形成的最佳权向量

  实际上波束形成就是通过调整权系数$w$，使得天线阵列在某一个方向上增益最大，也就是指向了某个方向。
  对不同的权向量，上式对来自不同方向的电波便有不同的响应，从而形成不同方向的空间波束。一般用移相器进行加权处理，即只调整信号相位，不改变信号幅度，因为信号在任一瞬间各阵元上的幅度是相同的。不难看出，若空间只有一个来自方向$\theta$的电波，其方向向量为$\alpha ({\theta }_k)$ ，则当权向量$w$取$\alpha ({\theta }_k)$时，输出$y(n)=\alpha ({\theta }_k{)}^H\alpha ({\theta }_k)=M$最大，实现导相定位作用。这时，各路的加权信号为相干叠加，称这一结果为空域匹配滤波。
  假设空间远场有一个期望信号$d(t)$(到达方向为${\theta }_d$)和$J$个不感兴趣的信号$i_j(t),j=1,\dots ,J$(称为干扰信号，其到达方向为${\theta }_{ij}$),令每个阵元都加上了高斯白噪声$n_k(t)$，它们具有相同的方差${\sigma }^2$。在这些假设下，第$k$个阵元上的接受信号可以表示为
$$x_k(t)=a_k({\theta }_d)d(t)+\sum _{j=1}^J{a}_k({\theta }_{ij})i_j(t)+n_k(t)$$$$\left(\begin{array}{c}{x}_1(t)\\ x_2(t)\\ ⋮\\ x_M(t)\end{array}\right)=\left(\begin{array}{c}a({\theta }_d),a({\theta }_{i1}),a({\theta }_{i2}),\dots ,a({\theta }_{ij})\end{array}\right)\left(\begin{array}{c}d(t)\\ i_1(t)\\ ⋮\\ i_J(t)\end{array}\right)+\left(\begin{array}{c}{n}_1(t)\\ n_2(t)\\ ⋮\\ n_M(t)\end{array}\right)$$

写成矩阵形式
$$x(t)=As(t)+n(t)=a({\theta }_d)d(t)+\sum _{j=1)}^{J}a({\theta }_{ij})i_j(t)+n(t)$$
$N$个快拍的波束形成器输出$t(t)=w^{H}x(t)(t=1,\dots ,N)的平均功率为$
$$P(w)=\frac{1}{N}\sum _{t=1}^N|y(t){|}^2=\frac{1}{N}\sum _{t=1}^N|w^{H}x(t){|}^2$$
化简得到
$P(w)=|w^{H}a({\theta }_d){|}^2\frac{1}{N}{\sum }_{t=1}^N|d(t){|}^2+{\sum }_{j=1}^N[\frac{1}{N}{\sum }_{i=1}^N|i_j(t){|}^2]|w_{H}a(\theta {)}_{ij}{|}^2+\frac{1}{N}||w|{|}^2{\sum }_{t=1}^N||n(t)|{|}^2$
当$N\to \infty$时，上式可以表示为
$$P(w)=E[|d(t){|}^2]|w^{H}a({\theta }_d){|}^2+\sum _{j=1}^{J}E[|i_j(t){|}^2]|w^{H}a({\theta }_{ij})|+\sigma ||w|{|}^2$$
  为了保证方向${\theta }_d$期望信号的正确接收，并完全抑制其他$J$个干扰，很容易根据上式得到关于权矢量的约束条件。
$$w^{H}a({\theta }_d)=1,w^{H}a({\theta }_{ij})=0$$
  这称为波束的迫零条件，因为它强迫接收阵列的波束方向图的“零点”指向所有的$J$个干扰信号。在以上两个约束条件下,$P(w)=E[|d(t){|}^2]+\sigma ||w|{|}^2$
实际上我们需要同时降低P(w)的后两项，一项是${\sum }_{j=1}^{J}E[|i_j(t){|}^2]|w^{H}a({\theta }_{ij})|$，这是来自其他方向的波信号，还有一项是我们引入的噪声$\sigma ||w|{|}^2$，当我们把前面一项强制置零时，会导致后面一项变大，所以我们要保证两者之和最小，所以我们只固定$$w^{H}a({\theta }_d)=1$$从而问题变成了在约束条件的约束下，求满足约束条件的权向量，有$$\underset{w}{\min }P(w)$$
实际上$P(w)=E[|y(t){|}^2]=w^{H}E[x(t)x^H(t)]w=w_{H}Rw$
式中，$R$为$x(t)$的协方差矩阵，实际上这个$P(w)$是总体的特征，而之前的是样本的特征，两个是差不多的意思。
所以我们把问题归结于，求满足约束条件的权矢量，有$$\underset{w}{\min }E[|y(t)|]=\underset{w}{\min }{w}^H\tilde{R}w$$这个问题可以利用Lagrange乘数法求解，令目标函数为
$$L(w)=w^H\tilde{R}w+\lambda [w^{H}a({\theta }_d)-1]$$方程两边对$w$求导，涉及到矩阵求导，本质上是对每个元素求导。
得到结果
$$\frac{\partial L}{\partial w}=2\tilde{R}w+\lambda a({\theta }_d)=0$$得到最优权矢量
$$w_{opt}=u{R}^{-1}a({\theta }_d)$$式中，$u$为一比例常数；${\theta }_d$是期望信号的波达方向。这样就可以决定$J+1$个发射信号的波束形成的最佳权向量。此时，波束形成器将只接收来自${\theta }_d$的信号，并一直其他波达方向的信号。
下面求$u$,注意到$w^{H}a({\theta }_d)=1$等价于$a^H({\theta }_d)\ast w=1$,上式两边乘$a^H({\theta }_d)$，可以求出$$u=\frac{1}{a^H({\theta }_d)R^{-1}a({\theta }_d)}$$故得到$$w_{opt}=\frac{R^{-1}a({\theta }_d)}{a^H({\theta }_d)R^{-1}a({\theta }_d)}$$
这样所有的公式的推导已经结束，我们得到了这个最优的权向量，我们抛开前面推导的公式不开，仅仅看最后的结果，可以发现，波束形成期的最佳权向量$w$取决于阵列方向向量$a({\theta }_k)$，也就是我们需要提前知道我们期望的信号到达的方向，即$a({\theta }_d)$，而在移动通信里这个方面一般是不知道的，这也是一个研究的方面，我下一篇再写，称为DoA估计，也就是估计信号的来向角度。

三、代码思路

推导了这么多，实际上我们需要的只是一个期望信号的角度方向，我们根据这个方向可以求出最优权矢量，使得天线方向图指向该角度。
代码其实也很简单。
假设我们本次仿真线性阵列，天线个数$M=18$,$\lambda =10$，间距$d=\lambda \ast 0.5$,期望信号从10°射入，有两个干扰信号从-30,30度射入。
代码流程如下：
1.最终接收到信号Xt的协方差矩阵
2.根据公式算出最优w
3.画出方向图

四、代码（MATLAB）

clc;
clear;
M = 18; % 天线数
lambda = 10;
d = lambda / 2;
L = 100;  %快拍数
thetas = [10];    % 期望信号入射角度
thetai = [-30 30]; % 干扰入射角度
n = [0:M-1]';
vs = exp(-1j * 2 * pi * n * d * sind(thetas) / lambda); % 信号方向向量
vn = exp(-1j * 2 * pi * n * d * sind(thetai) / lambda); % 干扰方向向量
f = 1600; % 载波频率
t = [0:L-1];
di = sin(2*pi*f*t/(8*f));    % 期望信号
vn1 = sin(2*pi*2 * f*t/(8*f));  % 干扰信号1 
vn2 = sin(2*pi*4 * f*t/(8*f));  % 干扰信号2 
A = [vs vn];
St = [di;vn1;vn2];
Xt = A*St + randn(M,L);   % 矩阵形式的公式
R_x = 1/L * (Xt * Xt');
R_x_inv = inv(R_x);
W_opt = R_x_inv * vs / (vs' * R_x_inv * vs);
% 测试此时的方向图
sita = 90 * [-1:0.001:1];
% 得到不同角度的方向矢量
v = exp(-1i*2*pi*n* d*sind(sita)/lambda);
B = abs(W_opt' * v);
plot(sita,20*log10(B/max(B)),'k')
title('波束图')
xlabel('角度/degree')
ylabel('波束图/dB')
grid on

结果如下：

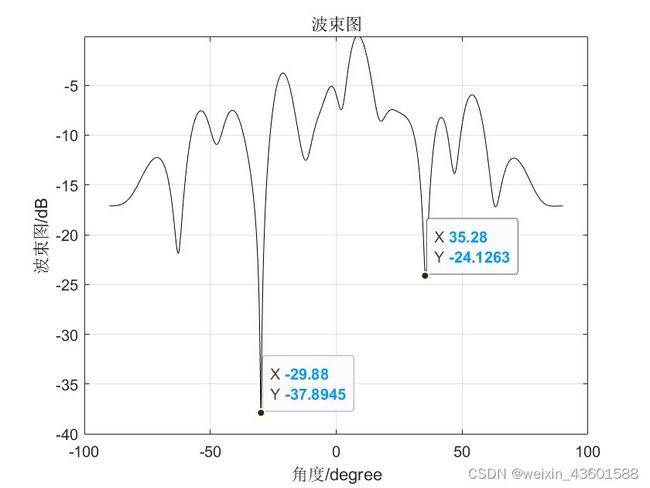
结果方向图，可以看出方向图指向了期望信号10度方向，干扰信号-30，30度都得到了相应的抑制。
本人也正在进行阵列信号处理的学习，欢迎大家交流。

主要参考：张小飞.阵列信号处理及MATLAB实现[M].电子工业出版社