最优控制理论 五、极大值原理→控制不等式约束

庞特里亚金提出的“极大值原理”（Pontryagin Maximum Principle,PMP）是最优控制理论的三大基石之一。与哈密尔顿函数法的异同是，两者都旨在解决非线性常微分方程组下的最优控制问题，都是性能指标取极值的必要条件。Hamiltonian解决分段连续可导的控制$u(t)$，而PMP可以求解不连续可导的控制，特别是不等式约束下的最优控制问题。

前面，最优控制理论 二、哈密尔顿函数法已经列举了各种类型的等式约束，采用Hamiltonian求解的方法，如：

• 终端等式约束$\psi (x(t_f),t_f)=0$
• 积分方程约束${\int }_0^{t_f}N(x(t),u(t),t)\text{d}t=\beta$
• 控制方程的非线性等式约束$N(u(t),t)=0$
• 状态变量的非线性等式约束$N(x(t),t)=0$

可是常见的不等式约束，Hamiltonian是难以解决的，如

• 控制输入受限$C(u(t),t)\le 0$
• 状态变量的路径约束$S(x(t),t)\le 0$，如火箭上升的过载约束
• 终端状态的不等式约束$S(x(t_f),t_f)\le 0$，如导弹命中脱靶量要求等

对于这些问题，采用PMP是很有必要的。解决另外两种形式的不等式约束下的OCP问题，在后续章节我会写出来。本篇博客限于篇幅，仅讨论控制输入受限的极大值原理方法，即$C(u(t),t)\le 0$。

1. 控制$u(t)$受约束的极小值原理

由于PMP的推导过程很复杂，所以这里只给出结论。文献[1]的2.4节应该有证明。
对于控制系统：
$$\begin{gathered} \dot{x}=f[x(t),u(t),t];x\left(t_o\right)=x_0{t}_o\le t\le t_f \\ \underset{u(t)\in U}{\min }J=\phi \left[x\left(t_f\right),t_f\right]+{\int }_{t_o}^{t_f}L[x(t),u(t),t]dt \end{gathered}$$

$t_f$给定或自由，问题要求受约束的最优控制$u(t)\in U\subset {\mathbb{R}}^q$，$U$为闭集，（简单理解闭集和开集，举例，闭集是$\{u|\Vert u\Vert \le 1\}$,开集是$\{u|\Vert u\Vert <1\}$。）实际上就是要满足形如下列形式的约束：
$$C(u(t),t)\le 0$$

对于这个问题，构造Hamilton函数如
$$H[x(t),u(t),\lambda (t),t]\triangleq L[x(t),u(t),t]+{\lambda }^{\mathrm{T}}(t)f[x(t),u(t),t]$$

沿最优轨线的状态方程、协态方程成立，表达为如下形式的Euler-Lagrange方程：
$$\begin{array}{rlr}\dot{\lambda }& =-\frac{\partial H}{\partial x}& \text{(协态方程)}\\ \dot{x}& =\frac{\partial H}{\partial \lambda }& \text{(状态方程)}\end{array}$$

而控制方程有新的形式
$$H(x^{\ast }(t),u^{\ast }(t),{\lambda }^{\ast }(t),t)=\underset{u\in U}{\min }H(x^{\ast }(t),u(t),{\lambda }^{\ast }(t),t)\text{\hspace{1em}(PMP)}$$

上式$(\text{PMP})$称为庞特里亚金的极小值原理，该式表明最优控制$u^{\ast }(t)$是所有容许的控制$u(t)\in U$当中使Hamilton函数取最小值的那个，即$u^{\ast }(t)=\{u|{\min }_{u(t)}H(x^{\ast },{\lambda }^{\ast },u,t),u\in U\}$。这个控制方程和无约束问题的$\frac{\partial H}{\partial u^{\ast }}=0$相比而言，将控制的集合推广到分段函数上，不必在整个区间内连续可导；相应地，在求解上需要分段求解$u^{\ast }(t)$。

上面协态方程、状态方程、控制方程(PMP)、边界条件等公式，共同组成性能指标取极值的必要条件。

注：若Hamiltonian取
$$H[x(t),u(t),\lambda (t),t]\triangleq -L+{\lambda }^{\mathrm{T}}f$$

则沿最优控制的必要条件为
$$H(x^{\ast }(t),u^{\ast }(t),{\lambda }^{\ast }(t),t)=\underset{u\in U}{\max }H(x^{\ast }(t),u(t),{\lambda }^{\ast }(t),t)$$

这个形式被称为极大值原理，也是庞特里亚金最早提出来的形式。这个方程在求解时和$\text{PMP}$等价，但是为了和前面章节的Hamiltonian保持一致，我们用极小值原理。$\square$

1.1 边界条件和横截条件

不同问题有不同的边界条件和横截条件，只有考虑全了，常微分方程组和两点边值问题才有可能定解。方程中$x(t),\lambda (t)\in {\mathbb{R}}^n,u(t)\in {\mathbb{R}}^q$总共有$2n+q$个未知的时变参数。协态方程和状态方程$x(t),\lambda (t)$是一阶常微分方程组，需要知道$2n$个边界条件才能求解；控制方程$u(t)$是代数方程，由$x(t)$和$\lambda (t)$分段求解得到。时间自由问题&最小时间问题的终端时刻$t_f$是未知数，需要多加一个边界条件。终端约束问题若有m个等式方程，则在$t_f$时刻多了m个未知的Lagrange乘数$\mu \in {\mathbb{R}}^m$.

下面直接把第二章的表格粘贴过来，利用PMP仍然需要套用这些条件，或者说Hamilton函数法和庞特里亚金极小值原理的边界条件、横截条件相同。

问题描述	未知变量个数（不包含$u(t)$）	边界条件	横截条件
$t_f,x_f$均给定	$2n$	$x(t_0)=x_0,x(t_f)=x_f$	\
$t_f$给定，$x_f$自由	$2n$	$x(t_0)=x_0$	$\lambda (t_f)=\frac{\partial \phi ({\cdot }^{\ast },t_f)}{\partial x}$
$t_f$自由，$x_f$给定	$2n+1$	$x(t_0)=x_0,x(t_f)=x_f$	$H({\cdot }^{\ast },t_f)+\frac{\partial \phi ({\cdot }^{\ast },t_f)}{\partial t}=0$
$t_f，x_f$均自由	$2n+1$	$x(t_0)=x_0$	$$\begin{gathered} \lambda (t_f)=\frac{\partial \phi }{\partial x}; \\ H({\cdot }^{\ast },t_f)+\frac{\partial \phi ({\cdot }^{\ast },t_f)}{\partial t}=0 \end{gathered}$$
$t_f$给定，$x_f$自由，且有终端约束$\psi (x_f,t_f)=0$	$2n+m$	$$\begin{gathered} x(t_0)=x_0 \\ \psi (x_f,t_f)=0 \end{gathered}$$	$\lambda (t_f)=\frac{\partial \phi }{\partial x}+{\mu }^{\mathrm{T}}\frac{\partial \psi }{\partial x}$
$t_f$给定，$x_f$自由，且有终端约束$\psi (x_f,t_f)=0$,(Lagrange型性能指标)	$2n+m$	$$\begin{gathered} x(t_0)=x_0 \\ \psi (x_f,t_f)=0 \end{gathered}$$	$\lambda (t_f)={\mu }^{\mathrm{T}}\frac{\partial \psi }{\partial x}$
$t_f，x_f$均自由，且有终端约束$\psi (x_f,t_f)=0$	$2n+m+1$	$$\begin{gathered} x(t_0)=x_0 \\ \psi (x_f,t_f)=0 \end{gathered}$$	$$\begin{gathered} \lambda (t_f)=\frac{\partial \phi }{\partial x}+{\mu }^{\mathrm{T}}\frac{\partial \psi }{\partial x}; \\ \frac{\partial \phi }{\partial t}+{\mu }^{\mathrm{T}}\frac{\partial \psi }{\partial t}+\left(\frac{\partial \phi }{\partial x}+{\mu }^{\mathrm{T}}\frac{\partial \psi }{\partial x}\right)f+L=0,(t=t_f) \end{gathered}$$
$t_f，x_f$均自由，且有终端约束$\psi (x_f,t_f)=0$,(Lagrange型性能指标)	$2n+m+1$	$$\begin{gathered} x(t_0)=x_0 \\ \psi (x_f,t_f)=0 \end{gathered}$$	$$\begin{gathered} \lambda (t_f)=\frac{\partial \phi }{\partial x}+{\mu }^{\mathrm{T}}\frac{\partial \psi }{\partial x}; \\ {\mu }^{\mathrm{T}}[\frac{\partial \psi }{\partial t}+\frac{\partial \psi }{\partial x}f]+L=0,(t=t_f) \end{gathered}$$

1.2 例1. 一维Riccati方程的PMP推导

对下面这个问题
$$\begin{gathered} \dot{x}(t)=x(t)+u(t),x(0)=x_0,0<t<t_f \\ \underset{u\in \mathbb{R}}{\min }J(x,u,t)={\int }_0^{t_f}{x}^2(t)+u^2(t)\text{d}t \end{gathered}$$

这个问题不考虑控制约束，即控制在开集$U\in \mathbb{R}$中且不受约束；$t_f$自由。这个问题可以看做无限时域线性二次型调节器问题的一种一维形式。下面采用极小值原理进行求解
$$H(x(t),\lambda (t),u(t),t)=x^2+u^2+\lambda (x+u)$$

写出协态方程
$$\begin{array}{rl}{\lambda }^{\prime }& =-\frac{\partial H}{\partial x}=-(2x+\lambda )\end{array}$$

按照庞特里亚金极大值原理写出控制方程并变形：
$$\begin{array}{rl}H(\ast ,u^{\ast }(t),t)& \le H(\ast ,u(t),t)\\ \Rightarrow x^{\ast 2}+u^{\ast 2}+{\lambda }^{\ast }(x^{\ast }+u^{\ast })& \le x^{\ast 2}+u^2+{\lambda }^{\ast }(x^{\ast }+u)\\ u^{\ast 2}+{\lambda }^{\ast }{u}^{\ast }& \le u^2+{\lambda }^{\ast }+u=g(u)\end{array}$$

等式左边小于等于右边的极小值，而右边的极小值，在极值点应有
$$\frac{\partial g(u)}{\partial u}=0\Rightarrow u_{min}=-{\lambda }^{\ast }/2$$

在无约束情况下，上式就是按照极小值条件求出的最优控制，即$u^{\ast }(t)=-{\lambda }^{\ast }(t)/2$. 将最优控制代入状态方程，
$$\{\begin{array}{c}{x}^{\prime }=x-\lambda /2\\ {\lambda }^{\prime }=-2x-\lambda \\ x(0)=x_0,\lambda (t_f)=0\end{array}$$

求解这个两点边值问题即可得到结果。如果进一步假设控制是反馈控制，即
$$u(t)=-k(t)x(t)$$

再考虑控制方程，并且定义一个变量$s(t)$
$$\lambda (t)=2k(t)x(t)\equiv s(t)x(t)\Rightarrow s(t)=\frac{\lambda (t)}{x(t)}$$

为了获得$s(t)$对时间的微分方程以便求解它，把$s(t)$对时间求全导数$$s^{\prime }=\frac{{\lambda }^{\prime }}{x}-\frac{\lambda x^{\prime }}{x^2}$$然后代入协态方程${\lambda }^{\prime }=-2x-\lambda$和状态方程$x^{\prime }=x-\lambda /2$得到：$$-s^{\prime }=2+2s-\frac{s^2}{2},s(t_f)=\lambda (t_f)/x=0$$

上式就是Riccati方程，高等数学中有求解初值问题$s(t)$的方法。它的矩阵形式为
$$-\dot{S}(t)=A^{\mathrm{T}}S+SA-SB{R}^{-1}{B}^{\mathrm{T}}S+Q,S(t_f)=S_f$$

事实上，利用PMP不仅可以解决控制受限的最优控制问题，而且也可以解决控制不受约束的问题，此时按照PMP推导出的结果和Hamilton函数方法的控制方程是完全等价的。

2. 最短时间控制问题

2.1 问题描述

设最短时间、终端约束的最优控制问题如下
$$\begin{gathered} \dot{x}(t)=f(x(t),t)+B(x(t),t)u(t) \\ u\in {\mathbb{R}}^q,|u_j(t)|<1,j=1,2,\cdots ,q \\ x(t_0)=x_0,\psi (x(t_f),t_f)=0,\psi \in {\mathbb{R}}^m \\ \underset{u(t)}{\min }J=t_f \end{gathered}$$

此问题的性能指标仅由一个到达时刻$t_f$构成。写出Hamilton函数
$$\begin{array}{rl}H& =1+{\lambda }^{\mathrm{T}}(f+Bu)=1+{\lambda }^{\mathrm{T}}f+u^{\mathrm{T}}(B^{\mathrm{T}}\lambda )\\ & =1+{\lambda }^{\mathrm{T}}f+\sum _{j=1}^q{u}_j({\lambda }^{\mathrm{T}}B(:,j))\end{array}$$

其中$B(:,j)$代表矩阵$B$的第$j$列所有元素，${\lambda }^{\mathrm{T}}B(:,j)=(n\ast 1{)}^{\mathrm{T}}\cdot (n\ast 1)\in \mathbb{R}$。这个系统的协态方程
$$\begin{gathered} \dot{\lambda }=-\frac{\partial H}{\partial x}=-\frac{\partial f^{\mathrm{T}}}{\partial x}\lambda -\sum _{j=1}^q{u}_j(\frac{\partial B(:,j{)}^{\mathrm{T}}}{\partial x}\lambda ) \\ =-[\frac{\partial f^{\mathrm{T}}}{\partial x}+\sum _{j=1}^q{u}_j(\frac{\partial B(:,j{)}^{\mathrm{T}}}{\partial x})]\lambda \end{gathered}$$

下面考察极小值原理，则对每个$u_j,j=1,2,\cdots ,q$，它的开关函数如下
$$u_j^{\ast }=\{\begin{array}{cc}-1,& {\lambda }^{\mathrm{T}}B(:,j)>0\\ 1,& {\lambda }^{\mathrm{T}}B(:,j)<0\\ others,& {\lambda }^{\mathrm{T}}B(:,j)=0\end{array}$$

需要注意的是，最小时间控制问题，若开关函数对$\forall t\in [0,t_f],{\lambda }^{\mathrm{T}}B(:,j)\ne 0$. 那么上面的第三项$\text{others}$就没有了，用正负号符号函数$\text{sign}$来表示这种形式的式子
$$u_j^{\ast }=-\text{sign}\{{\lambda }^{\mathrm{T}}B(:,j)\}$$

这种形式的控制要么是最大值，要么是最小值，称为Bang-Bang控制。可证明在最大与最小之间的切换次数是有限的。

2.2 例2. 二次积分时间最优控制

对于二次积分系统，若初始和终端条件给定，控制幅值受限，最小到达时间。问题如下
$$\begin{gathered} {\dot{x}}_1(t)=x_2(t),{\dot{x}}_2(t)=u(t) \\ \mathbf{x}(0)=[x_1,x_2],\mathbf{x}(t_f)=[0,0] \\ \underset{|u(t)|\le 1}{\min }J={\int }_0^{t_f}1\text{d}t=t_f \end{gathered}$$

这个问题可以看做最小时间控制问题的一维形式。首先构建Hamilton函数
$$H(x(t),\lambda (t),u(t),t)=1+{\lambda }_1{x}_2+{\lambda }_{2}u$$

由极小值原理

3. 燃料最优控制

3.1 最小燃料消耗问题

设最小燃料消耗问题如下
$$\begin{gathered} \dot{x}(t)=f(x(t),t)+B(x(t),t)u(t) \\ u\in {\mathbb{R}}^q,|u_j(t)|<1,j=1,2,\cdots ,q \\ x(t_0)=x_0,\psi (x(t_f),t_f)=0,\psi \in {\mathbb{R}}^m \\ \underset{u(t)}{\min }J={\int }_0^{t_f}\sum _{j=1}^q{w}_j|u_j(t)|\text{d}t \end{gathered}$$

此问题的性能指标当中，各个控制分量的权重$w_i>0$为常数；终端时刻$t_f$自由或固定。写出Hamilton函数
$$\begin{array}{rl}H& =\sum _{j=1}^q{w}_j|u_j(t)|+{\lambda }^{\mathrm{T}}(f+Bu)\\ & ={\lambda }^{\mathrm{T}}f+\sum _{j=1}^q{w}_j|u_j(t)|+u_j[{\lambda }^{\mathrm{T}}B(:,j)]\end{array}$$

这个系统的协态方程与上面的问题一样
$$\begin{gathered} \dot{\lambda }=-\frac{\partial H}{\partial x} \\ =-\frac{\partial f^{\mathrm{T}}}{\partial x}\lambda -\sum _{j=1}^q{u}_j(\frac{\partial B(:,j{)}^{\mathrm{T}}}{\partial x}\lambda )=-[\frac{\partial f^{\mathrm{T}}}{\partial x}+\sum _{j=1}^q{u}_j(\frac{\partial B(:,j{)}^{\mathrm{T}}}{\partial x})]\lambda \end{gathered}$$

下面考察极小值原理，则对每个$u_j,j=1,2,\cdots ,q$，需要考虑
$$\sum _{j=1}^q{w}_j|u_j^{\ast }(t)|+u_j^{\ast }[{\lambda }^{\mathrm{T}}B(:,j)]\le \sum _{j=1}^q{w}_j|u_j(t)|+u_j[{\lambda }^{\mathrm{T}}B(:,j)]$$

为了具体知道参数对于最优控制的影响，定义
$$g(u_j)\triangleq |u_j(t)|+\frac{{\lambda }^{\mathrm{T}}B(:,j)}{w_j}{u}_j=|u_j(t)|+p_j\cdot u_j$$

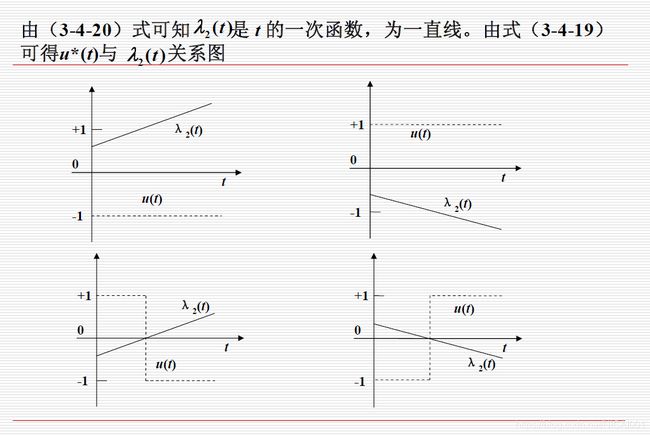
上式定义的函数$g(u_j)$的函数曲线是分段线性的，而且它分两段，具体的取值可以看下面的图

$p_j<-1$	$p_j\in (-1,0)$	$p_j\in (0,1)$	$p_j>1$
图1	图2	图3	图4
$u_j^{\ast }=1$	$u_j^{\ast }=0$	$u_j^{\ast }=0$	$u_j^{\ast }=-1$

考虑到控制受限$|u_j(t)|\le 1$，于是最优控制的取值如下
$$u_j^{\ast }=\{\begin{array}{cc}1,& p_j<-1\\ \exists u_j\in [0,1],& p_j=-1\\ 0,& p_j\in (-1,1)\\ \exists u_j\in [-1,0],& p_j=1\\ -1,& p_j>1\end{array}$$
其中的$p_j={\lambda }^{\mathrm{T}}B(:,j)/w_j$.控制方程中的$\exists u_j\in [0,1]$代表控制处在这个区间，具体的求解方法属于奇异最优控制理论的范畴。在此暂时不给出。

注2： 若控制的约束为$u_j(t)\in [0,1]$，看图可得最小的Hamiltonian在这些点取得
$$u_j^{\ast }=\{\begin{array}{cc}1,& p_j<-1\\ \exists u_j\in [0,1],& p_j=-1\\ 0,& p_j>-1\end{array}$$

3.2 例3. 二次积分燃料最优控制

系统模型不变，性能指标改变
$$\begin{gathered} {\dot{x}}_1(t)=x_2(t),{\dot{x}}_2(t)=u(t) \\ \mathbf{x}(0)=[x_{10},x_{20}],\mathbf{x}(t_f)=[0,0],t_f\text{ free} \\ \underset{|u(t)|\le 1}{\min }J={\int }_0^{t_f}|u|\text{d}t \end{gathered}$$

这个问题可以看做最优燃料问题的一维形式。构建Hamilton函数、
$$H(x(t),\lambda (t),u(t),t)=|u|+{\lambda }_1{x}_2+{\lambda }_{2}u$$

其协态方程和边界条件很容易写出，在此略去。根据极小值原理，控制方程有：
$$|u^{\ast }|+{\lambda }_2{u}^{\ast }\le |u|+{\lambda }_{2}u=g(u)$$

$u^{\ast }$取函数$g(u)$的最小值，而函数$g(u)$只受${\lambda }_2$影响，不同取值有不同的形态，而这结果与多维问题的图一样。

${\lambda }_2<-1$	${\lambda }_2\in (-1,0)$	${\lambda }_2\in (0,1)$	${\lambda }_2>1$
如图1	如图2	如图3	如图4
$u^{\ast }=1$	$u^{\ast }=0$	$u^{\ast }=0$	$u^{\ast }=-1$

最优控制律为
$$u^{\ast }=\{\begin{array}{cc}-\text{sign}({\lambda }_2),& |{\lambda }_2|>1\\ 0,& |{\lambda }_2|<1\\ \exists u\in [0,1],& {\lambda }_2=-1\\ \exists u\in [-1,0],& {\lambda }_2=1\end{array}$$
在${\lambda }_2=\pm 1$时，控制并不是任意的，而是有进一步的判定条件。有关奇异弧段最优控制的相关方法，请参考具体文献。

4. 数值求解

极大值原理求解最优控制问题属于间接法，它的数值求解基本思路仍然是求解Hamilton系统，也就是包含状态$x(t)$,协态$\lambda (t)$的变化。它与Hamilton函数法求解的主要区别是，状态方程和协态方程是间断性的，也就是在开关开2种系统方程之间切换，这样构成的问题属于多点边值问题。类似于前面最优控制理论 三、两点边值问题求解这一节的思路，主要求解步骤是猜测协态变量的初始值$\lambda (t_0)$，然后代入求解Bang-Bang控制的哈密尔顿系统，通过非线性方程求根方法得到准确的协态初值，积分这个ODE系统自然能得到最优控制的解析解$u(x,\lambda )$。

参考文献

[1] 邢继祥. 最优控制应用基础 Sec 2.4~Sec 2.8 [M]. 科学出版社, 2003.
[2] Bryson A E , Ho Y C ,Applied optimal control : optimization, estimation, and control Sec 3.8~Sec 3.12 [J]. IEEE Transactions on Systems Man & Cybernetics, 1975
[3] MIT OpenCourseWare 16.323 Principles of Optimal Control - Lecture 9: Constrained Optimal Control
[4] 百度文库-3. 极大值原理
[5] CSDN - An Introduction to Mathematical Optimal Control Theory-Notes v2.0.pdf- Ch.4 The Pontryagin Maximum Principle [M] Lawrence C. Evans (American Math Society, 2013) 原文链接