量化投资学习——A股H股套利年化100%
一、交易对象选取
首先是选取数据,选取数据的来源是wind:
从wind中的交易数据-AH比较 里面可以看到历史收盘价和A/H溢价率, 考虑到在2008年金融危机之后,全球市场发生了较大的变化,我们从2009年取,一共取到了13年的数据如下所示,其中表1是AH溢折数据,价格数据和volume数据
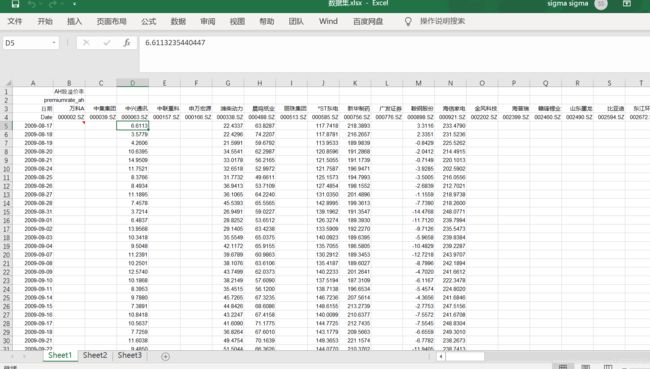
接下来进行数据分析:根据十三年的数据,我们观察得到,每年由于新上市的股票数目由于上市退市等变动,存在着较大的变化,考虑到题目要求,我们对于股票数据进行滚动设定,即每一个月进行判断股票的协整情况,选择合适的协整股票,在下一个月进行统计配对交易,并且根据股票的交易情况,不断更新股票,去掉ST和停牌情况
首先读取股票数据,我们读取的数据集为三部分,AH股溢折价数据,价格数据和volume数据,其中对于AH股
AH溢折价数据 = (指定日A股股价 x 汇率/H股股价)-1)x 100
以2009年的数据为例,我们首先对数据进行一个可视化的分析,如下所示:
import pandas as pd
import numpy as np
由于要展示的股票数目过多,所以使用以下语句来展示所有的数据
pd.options.display.max_columns = None
pd.options.display.max_rows = None
由于要画图,为了防止汉字没有办法正常显示,所以要进行一个设置
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
隐藏警告
import warnings
warnings.filterwarnings('ignore')
data_AH = pd.read_excel('data/'+'数据集.xlsx',sheet_name=0,skiprows=2,index_col=0) #AH溢折
data_price = pd.read_excel('data/'+'数据集.xlsx',sheet_name=1,skiprows=2,index_col=0)#价格
data_AH.head()
| 万科A | 中集集团 | 中兴通讯 | 中联重科 | 申万宏源 | 潍柴动力 | 晨鸣纸业 | 丽珠集团 | *ST东电 | 新华制药 | ... | *ST拉夏 | 药明康德 | 洛阳钼业 | 德利股份 | 中国通号 | 君实生物-U | 康希诺-U | 昊海生科 | 复旦微电 | 复旦张江 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 日期 | |||||||||||||||||||||
| Date | 000002.SZ | 000039.SZ | 000063.SZ | 000157.SZ | 000166.SZ | 000338.SZ | 000488.SZ | 000513.SZ | 000585.SZ | 000756.SZ | ... | 603157.SH | 603259.SH | 603993.SH | 605198.SH | 688009.SH | 688180.SH | 688185.SH | 688366.SH | 688385.SH | 688505.SH |
| 2009-08-17 00:00:00 | NaN | NaN | 6.61132 | NaN | NaN | 22.4337 | 63.8287 | NaN | 117.742 | 218.389 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2009-08-18 00:00:00 | NaN | NaN | 3.57788 | NaN | NaN | 22.4296 | 74.2207 | NaN | 117.878 | 216.266 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2009-08-19 00:00:00 | NaN | NaN | 4.26058 | NaN | NaN | 21.5991 | 59.6792 | NaN | 113.953 | 189.984 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2009-08-20 00:00:00 | NaN | NaN | 10.6395 | NaN | NaN | 34.5541 | 62.2987 | NaN | 120.86 | 191.287 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
5 rows × 133 columns
从上图观察到,一些公司由于未上市原因,出现了NaN的情况,然后一些公司出现了ST标识,因此我们把ST股票去掉,另一个比较有趣的现象是,在早期时候可以发现很多股票AH溢折很大
data_AH = data_AH[[i for i in data_AH.columns if i.find('*ST')==-1]]
data_price = data_price[[i for i in data_price.columns if i.find('*ST')==-1]]
data_AH.head()
| 万科A | 中集集团 | 中兴通讯 | 中联重科 | 申万宏源 | 潍柴动力 | 晨鸣纸业 | 丽珠集团 | 新华制药 | 广发证券 | ... | 昭衍新药 | 药明康德 | 洛阳钼业 | 德利股份 | 中国通号 | 君实生物-U | 康希诺-U | 昊海生科 | 复旦微电 | 复旦张江 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 日期 | |||||||||||||||||||||
| Date | 000002.SZ | 000039.SZ | 000063.SZ | 000157.SZ | 000166.SZ | 000338.SZ | 000488.SZ | 000513.SZ | 000756.SZ | 000776.SZ | ... | 603127.SH | 603259.SH | 603993.SH | 605198.SH | 688009.SH | 688180.SH | 688185.SH | 688366.SH | 688385.SH | 688505.SH |
| 2009-08-17 00:00:00 | NaN | NaN | 6.61132 | NaN | NaN | 22.4337 | 63.8287 | NaN | 218.389 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2009-08-18 00:00:00 | NaN | NaN | 3.57788 | NaN | NaN | 22.4296 | 74.2207 | NaN | 216.266 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2009-08-19 00:00:00 | NaN | NaN | 4.26058 | NaN | NaN | 21.5991 | 59.6792 | NaN | 189.984 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2009-08-20 00:00:00 | NaN | NaN | 10.6395 | NaN | NaN | 34.5541 | 62.2987 | NaN | 191.287 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
5 rows × 131 columns
我们发现第一行数据和表头重复,为了后续处理方便,把第一行数据删除
data_AH = data_AH.iloc[1:,:]
data_price = data_price.iloc[1:,:]
data_AH.head()
| 万科A | 中集集团 | 中兴通讯 | 中联重科 | 申万宏源 | 潍柴动力 | 晨鸣纸业 | 丽珠集团 | 新华制药 | 广发证券 | ... | 昭衍新药 | 药明康德 | 洛阳钼业 | 德利股份 | 中国通号 | 君实生物-U | 康希诺-U | 昊海生科 | 复旦微电 | 复旦张江 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 日期 | |||||||||||||||||||||
| 2009-08-17 00:00:00 | NaN | NaN | 6.61132 | NaN | NaN | 22.4337 | 63.8287 | NaN | 218.389 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2009-08-18 00:00:00 | NaN | NaN | 3.57788 | NaN | NaN | 22.4296 | 74.2207 | NaN | 216.266 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2009-08-19 00:00:00 | NaN | NaN | 4.26058 | NaN | NaN | 21.5991 | 59.6792 | NaN | 189.984 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2009-08-20 00:00:00 | NaN | NaN | 10.6395 | NaN | NaN | 34.5541 | 62.2987 | NaN | 191.287 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2009-08-21 00:00:00 | NaN | NaN | 14.9509 | NaN | NaN | 33.0178 | 56.2165 | NaN | 191.174 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
5 rows × 131 columns
data_AH = data_AH.astype(float)
data_price = data_price.astype(float)
对价格的处理,由于我们进行AH套利,是对AH股价差进行建模,需要对股票的H股价格数据进行复原
根据公式 AH溢折价数据 = (指定日A股股价 x 汇率/H股股价)-1)x 100,故有:
汇率调整的H价格 = 指定日A股股价/(AH溢折价数据/100+1)
故:
data_Hprice = data_price/(data_AH/100+1)
为了方便处理数据,我们把上述的两份数据按照日期进行遍历,对于股票数据进行滚动设定,即每六个月进行判断股票的协整情况,选择合适的协整股票,在下一个月进行统计配对交易,并且根据股票的交易情况,不断更新股票
date_range = pd.date_range(start='2009-08-01', end='2021-08-01', freq='MS')+ pd.DateOffset(days=14)
date_range
DatetimeIndex(['2009-08-15', '2009-09-15', '2009-10-15', '2009-11-15',
'2009-12-15', '2010-01-15', '2010-02-15', '2010-03-15',
'2010-04-15', '2010-05-15',
...
'2020-11-15', '2020-12-15', '2021-01-15', '2021-02-15',
'2021-03-15', '2021-04-15', '2021-05-15', '2021-06-15',
'2021-07-15', '2021-08-15'],
dtype='datetime64[ns]', length=145, freq=None)
这里取出2009年8月到2010年2月之间为一个样例,分析这七个月的情况
首先读取的是用于计算指标的数据,如下所示:
#港股价格
data_Htrain = data_Hprice.loc[date_range[0]:date_range[6]] #取2009年8月到2010年1月,计算股票之间的相关性
data_Htrain = data_Htrain.fillna(method='ffill') #在计算相关性的时间段,对于其中有少部分缺失(停牌)的数据进行向上填充,即使用前一天的数据来填补
data_Htrain = data_Htrain.dropna(how='any',axis=1) #去除未上市或者仍有缺失的数据
#A股价格
data_Atrain = data_price.loc[date_range[0]:date_range[6]]
data_Atrain = data_Atrain.fillna(method='ffill').dropna(how='any',axis=1)
#AH溢折价
data_AHtrain = data_AH.loc[date_range[0]:date_range[6]] #取这段时间的AH溢折价
data_AHtrain = data_AHtrain.fillna(method='ffill').dropna(how='any',axis=1)
其次是用于交易的数据,如下所示:
#港股价格
data_Htest = data_Hprice.loc[date_range[6]:date_range[7]] #取2009年8月到2010年1月,计算股票之间的相关性
data_Htest = data_Htest.fillna(method='ffill') #在计算相关性的时间段,对于其中有少部分缺失(停牌)的数据进行向上填充,即使用前一天的数据来填补
data_Htest = data_Htest.dropna(how='any',axis=1) #去除未上市或者仍有缺失的数据
#A股价格
data_Atest = data_price.loc[date_range[6]:date_range[7]]
data_Atest = data_Atest.fillna(method='ffill').dropna(how='any',axis=1)
#AH溢折价
data_AHtest = data_AH.loc[date_range[6]:date_range[7]] #取这段时间的AH溢折价
data_AHtest = data_AHtest.fillna(method='ffill').dropna(how='any',axis=1)
计算股票之间的相关性,由于股票数据分布不是正态分布,故在此处使用斯皮尔曼相关性进行计算
data_corr = data_Htrain.corrwith(data_Atrain, method='spearman')
data_corr
中兴通讯 0.733974
潍柴动力 0.778756
晨鸣纸业 0.706747
新华制药 0.930001
鞍钢股份 0.832888
海信家电 0.884199
华能国际 0.013937
皖通高速 0.836945
中远海能 0.687462
华电国际 0.159516
中国石化 0.343717
南方航空 0.719657
招商银行 0.919855
中国东航 0.737950
兖州煤业 0.914340
白云山 0.787349
江西铜业 0.911707
宁沪高速 0.765715
深高速 -0.054893
海螺水泥 0.307993
青岛啤酒 0.924166
中船防务 0.468789
上海石化 0.478368
南京熊猫 0.870209
马钢股份 0.845260
京城股份 0.938941
石化油服 0.806187
创业环保 0.902609
东方电气 0.607466
洛阳玻璃 0.578598
重庆钢铁 0.417819
中国神华 0.725900
四川成渝 0.680802
中国国航 0.915117
中国铁建 0.310747
中国平安 0.895591
交通银行 0.513391
广深铁路 -0.117188
中国中铁 0.129269
工商银行 0.914482
北辰实业 0.612741
中国铝业 0.448600
中国人寿 0.920370
上海电气 0.396375
中国中车 0.852950
中海油服 0.681948
中国石油 0.569487
中远海发 0.489644
中煤能源 0.718966
紫金矿业 0.857401
中远海控 0.705750
建设银行 0.799872
中国银行 0.388159
大唐发电 0.571597
中信银行 0.714665
万科A NaN
上海医药 NaN
中信证券 NaN
中国太保 NaN
中联重科 NaN
中集集团 NaN
丽珠集团 NaN
复星医药 NaN
大众公用 NaN
山东黄金 NaN
广发证券 NaN
民生银行 NaN
海尔智家 NaN
海通证券 NaN
福耀玻璃 NaN
金风科技 NaN
dtype: float64
由上可以看出,在2009年8月到9月之间,有若干只股票的A股和H股相关性比较大,其中,出现NaN的股票可能是由于其A(H)股未上市,所以导致数据无法显示,为了进一步使策略可以自适应选择合适的股票对,对于上述存在关联的股票中,我们选取相关性大于75%分位数进行操作,如下所示
data_corr_used = data_corr[data_corr>data_corr.quantile(0.75)]
data_corr_used
新华制药 0.930001
海信家电 0.884199
招商银行 0.919855
兖州煤业 0.914340
江西铜业 0.911707
青岛啤酒 0.924166
南京熊猫 0.870209
京城股份 0.938941
创业环保 0.902609
中国国航 0.915117
中国平安 0.895591
工商银行 0.914482
中国人寿 0.920370
紫金矿业 0.857401
dtype: float64
以新华制药为例,在上述股票中,它的A股和H股股价的相关性是最高的,接下来我们利用协整理论来分析新华制药A股和H股是否满足配对交易的条件
ADF检验
下面对这两组数据进行平稳性检验。
from statsmodels.tsa.stattools import adfuller
result_A = adfuller(data_Atrain['新华制药'])
result_H = adfuller(data_Htrain['新华制药'])
print(result_A)
print(result_H)
(-1.4431310213630189, 0.5614329499694334, 4, 118, {'1%': -3.4870216863700767, '5%': -2.8863625166643136, '10%': -2.580009026141913}, -87.58482797037456)
(-1.503622297562152, 0.5317186850955914, 0, 122, {'1%': -3.4851223522012855, '5%': -2.88553750045158, '10%': -2.5795685622144586}, -352.8340635801403)
从结果可以看出 t-statistic 的值要大于10%,所以说无法拒绝原假设,也就是原数据都是非平稳的。
下面进行一阶差分之后检查一下:
from statsmodels.tsa.stattools import adfuller
result_A = adfuller(np.diff(data_Atrain['新华制药']))
result_H = adfuller(np.diff(data_Htrain['新华制药']))
print(result_A)
print(result_H)
(-6.79882907947638, 2.264371725491006e-09, 3, 118, {'1%': -3.4870216863700767, '5%': -2.8863625166643136, '10%': -2.580009026141913}, -85.47530269642459)
(-6.175010014868815, 6.663231093369651e-08, 5, 116, {'1%': -3.4880216384691867, '5%': -2.8867966864160075, '10%': -2.5802408234244947}, -349.6414355474592)
结果可以看出,一阶差分之后的数据是平稳的,也就是说原数据是一阶单整的,满足协整关系的前提,所以下一步我们对这两组数据进行协整检验,来探究两者是否是协整的。
协整检验
from statsmodels.tsa.stattools import coint
print(coint(np.diff(data_Atrain['新华制药']), np.diff(data_Htrain['新华制药'])))
(-11.816452883662702, 1.0013043392750406e-20, array([-3.98924151, -3.38709271, -3.07968702]))
结果看出 t-statistic 小于5%,所以说有95%的把握说两者具有协整关系。
基于以上条件,在进行后续的策略构造的时候,同样的,对于以上根据相关性方法挑选出来的数据,也要进行以上两步的筛选,只有当满足筛选条件的股票,才纳入到股票池中
考虑到我们的数据中有AH溢折价数据,所以直接使用溢折价数据进行策略构建,还是以新华制药为例,我们计算出该序列的均值,差价围绕着均值上下波动,再计算出方差,并画图如下所示:
sigma = np.std(data_AHtrain['新华制药'])
miu = np.mean(data_AHtrain['新华制药'])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(len(data_AHtrain['新华制药'])), data_AHtrain['新华制药'])
ax.hlines(miu, 0, len(data_AHtrain['新华制药']))
ax.hlines(1.5 * sigma+miu, 0, len(data_AHtrain['新华制药']), colors='b')
ax.hlines(-1.5 * sigma+miu, 0, len(data_AHtrain['新华制药']), colors='b')
ax.hlines(2.5 * sigma+miu, 0, len(data_AHtrain['新华制药']), colors='r')
ax.hlines(-2.5 * sigma+miu, 0, len(data_AHtrain['新华制药']), colors='r')
我们计算出该序列的均值,差价围绕着均值上下波动,再计算出方差:
当差价大于均值加1.5个方差时,看空差价,即差价向上偏离均值太多了,操作上做多H股做空A股
当差价大于均值减1.5个方差时,看多差价,即差价向下偏离均值太多了,操作上做多A股做空H股
止损设置为二点五倍标准差
主体策略
下面将构建配对交易的策略,统计套利的关键是要保证策略的市场中性,也就是说无论市场的趋势是上升还是下降,都要使策略或者预期的收益为正。
投资组合的构建
配对交易主要分析的对象是两个品种价格之间的偏离,由均值回归理论知,在股票、期货或者其他金融衍生品的交易市场中,无论高于或低于价值中枢(或均值)都有很高的概率向价值中枢回归的趋势。所以说,在具有协整关系的这两组数据中,当它们两者的价差高与均值时则会有向低走的趋势,价差低于均值时则会有向高走的趋势。
注意这里直接研究的是 A、B 价格差值,统计套利策略中通常会将 B 价格乘以一个协整系数,研究的对象是它们的残差,由于协整检验后可以知道它们的残差具有平稳性,所以更好的应用均值回归的理论。
设置开仓和止损的阈值
为了使开仓和止损的阈值更好地比较,所以就将开仓阈值设置为窗口内数据的两倍标准差,止损设置为三倍标准差。这个标准差的倍数可以通过调参来不断调优,标准差的设置也可以通过 GARCH 等模型拟合的自回归条件异方差类似的时变标准差来代替。
def strategy(price_A,price_H,data_AH):
spread = data_AH # 读取AH溢折数据
mspread = spread - np.mean(spread)
sigma = np.std(mspread)
open = 1.5 * sigma
stop = 2.5 * sigma
profit_list = []
hold = False
hold_price_A = 0
hold_price_H = 0
hold_state = 0 # 1 (A:long H:short) -1 (A:short H:long)
profit = 0
for i in range(len(price_A)):
if hold == False:
if mspread[i] >= open:
hold_price_A = price_A[i]
hold_price_H = price_H[i]
hold_state = -1
hold = True
elif mspread[i] <= -open:
hold_price_A = price_A[i]
hold_price_H = price_H[i]
hold_state = 1
hold = True
else:
# print('hold_price_A:',hold_price_A)
# print('hold_price_H:',hold_price_H)
if mspread[i] >= stop and hold_state == -1 :
profit = (hold_price_A - price_A[i])/hold_price_A + (price_H[i] - hold_price_H)/hold_price_H
# print('冲破止损线,A:long H:short',profit)
hold_state = 0
hold = False
if mspread[i] <= -stop and hold_state == 1 :
profit = (price_A[i] - hold_price_A)/hold_price_A + (hold_price_H - price_H[i])/hold_price_H
# print('冲破止损线,A:short H:long',profit)
hold_state = 0
hold = False
if mspread[i] <= 0 and hold_state == -1:
profit = (hold_price_A - price_A[i])/hold_price_A + (price_H[i] - hold_price_H)/hold_price_H
# print('开仓,A:short H:long',profit)
hold_state = 0
hold = False
if mspread[i] >= 0 and hold_state == 1:
profit = (price_A[i] - hold_price_A)/hold_price_A + (hold_price_H - price_H[i])/hold_price_H
# print('开仓,A:long H:short',profit)
hold_state = 0
hold = False
profit_list.append(profit)
profit = 0
# print(profit_list)
return profit_list
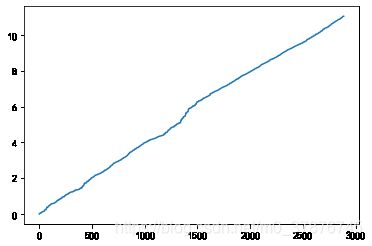
最终我们绘制出新华制药AH股差价套利策略的净值走势图:
profit_list = strategy(data_Atest['海信家电'],data_Htest['海信家电'],data_AHtest['海信家电'])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(len(profit_list)), np.cumsum(profit_list))
plt.show()
开仓,A:short H:long 0.0921522222621323
[0, 0, 0, 0, 0.0921522222621323, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
可以看出回测结果看似是比较让人满意的,而且我们并没有对参数进行调优,从上图可以知道统计套利单次的收益是比较薄弱的,主要原因不仅仅是价差带来的这种相对收益本来就比较低,还有就是止损阈值设置的问题,有时一次止损就会cover掉之前所有的收益。所以说在统计套利中,阈值的设置是非常重要的。
此外,在日后的更新中,还要考虑以下的问题:
1、在选择配对数据的品种时,除了要考虑配对品种的相关性之外,还要考虑品种的市场流动性等因素。
2、历史回测时,还需要将手续费、滑点等因素考虑进去。
接下来,我们考虑对多个股票进行操作,首先为了更接近真实条件,我们根据真实的佣金费率进行了设置:
# 股票类交易手续费是:买入时佣金万分之三,卖出时佣金万分之三加千分之一印花税, 每笔交易佣金最低扣5块钱
open_tax=0
close_tax=0.001
open_commission=0.00015
close_commission=0.00015
根据前面的介绍,我们在12年间,进行滚动向前的进行测试
根据前面选择股票的方法,我们构造了如下的函数进行股票选择,并进行测试如下所示:
np.array([1,2])+np.array([3,4])
array([4, 6])
def select_stock(price_A,price_H):
selected_stock_list = []
data_corr_selected = price_H.corrwith(price_A, method='spearman')
data_corr_selected = data_corr_selected[data_corr_selected>data_corr_selected.quantile(0.75)]
for selected_stock in data_corr_selected.index:
coint_value = float(coint(np.diff(price_A[selected_stock]), np.diff(price_H[selected_stock]))[0])
if coint_value<-3.98924151:
selected_stock_list.append(selected_stock)
return selected_stock_list
select_stock(data_Atest,data_Htest)
['民生银行', '四川成渝', '中国铁建', '中国平安', '中国人寿']
import pandas as pd
profit_list = []
#把股票根据日期进行分组,一次读取七个月的数据,进行轮动,前六个月的数据用来测试,第七个月用来交易
for i in range(len(date_range[:-7])):
data_sub_Hprice = data_Hprice.loc[date_range[i]:date_range[i+7]].fillna(method='ffill').dropna(how='any',axis=1) #去除这七个月中存在停牌的股票
data_sub_Aprice = data_price.loc[date_range[i]:date_range[i+7]].fillna(method='ffill').dropna(how='any',axis=1) #去除这七个月中存在停牌的股票
data_sub_AH = data_AH.loc[date_range[i]:date_range[i+7]].fillna(method='ffill').dropna(how='any',axis=1)
return_array = np.array([0.0]*len(data_sub_Aprice.loc[date_range[i+6]:date_range[i+7]]))
stock_list_used = select_stock(data_sub_Aprice.loc[:date_range[i+6]],data_sub_Hprice.loc[:date_range[i+6]])
for stock in stock_list_used:
# print(stock)
return_array +=np.array(strategy(data_sub_Aprice.loc[date_range[i+6]:date_range[i+7],stock],data_sub_Hprice.loc[date_range[i+6]:date_range[i+7],stock],data_sub_AH.loc[date_range[i+6]:date_range[i+7],stock]))
# print(return_array)
profit_list+=list((return_array)/len(stock_list_used))
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(len(profit_list)), np.cumsum(profit_list))
plt.show()
一些感觉有用的文献还是要写在最后的:
Is pairs trading profitable on China AH-share markets?