深度学习系列 | 解读LeNet及PyTorch实现
论文原文:Gradient-Based Learning Applied to Document Recognition
LeNet的整体结构
- 0. Input
- 1. C1:input_size = 32×32 ,output_size = 6@28×28
- 2. S2:input_size = 6@28×28 ,output_size = 6@14×14
- 3. C3:input_size = 6@14×14,output_size = 16@10×10
- 4. S4:input_size = 16@10×10 ,output_size = 16@5×5
- 5. C5:input_size = 16@5×5 ,output_size = 120@1×1
- 6. F6:input_size = 120 ,output_size = 84
- 7. OUTPUT:input_size = 84 ,output_size = 10
Fig 1展示的是LeNet的整体结构:
LeNet包括7个layers(不包括Input),Fig 1中的C、S和F分别指卷积层、下采样层(池化层)和全连接层,其后所跟随的数字1-6指所在层的索引位置。例如,S2意为在网络结构中索引为2的位置的下采样层。
0. Input
LeNet是设计用于识别手写数字,其Input为32×32的灰度图像(即通道数channels为1),可视作一个二维的matrix。如有兴趣,也可以自行将Input改为彩色图像,只需在LeNet代码中将channels改为3即可,此时是一个三维的tensor。
1. C1:input_size = 32×32 ,output_size = 6@28×28
C1层存在6个卷积核,卷积核大小为5×5,步长stride=1。
Fig 1中展示了经过C1层输出的feature map(特征图)为6@28×28,意为经C1层输出6个28×28大小的特征图。
2. S2:input_size = 6@28×28 ,output_size = 6@14×14
S2层为下采样层(也可称为池化层),这里使用的不是Max Pooling(很多文章将此处写为Max Pooling,可参见原文的叙述Fig 2),其实比较类似Average Pooling。
池化层大小为2×2,该2×2区域内的元素加总后乘以一个系数,再加上一个偏置后,送入Sigmoid激活函数,得到的值即为该2×2区域Subsampling后的值,因此经过S2层后,特征图大小的尺寸缩小一半,即为6@14×14(池化不改变通道数)。
ps. 由于原论文篇幅过长(46页),我没有找到这个trainable coefficient和trainable bias的值具体取了多少,所以我说的是S2层的操作类似于平均池化。
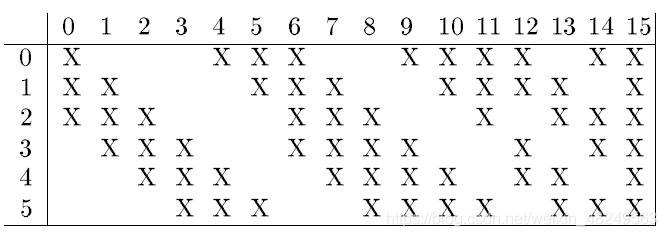
3. C3:input_size = 6@14×14,output_size = 16@10×10
C3层为16个5×5大小的卷积核(步长依旧为1),但是卷积时并没有一次性使用S2输出的6个特征图,而是对6个特征图进行了组合使用,组合方式见Fig 3。
例如,经C3层输出的第0个特征图,是由S2输出的6个特征图中的第0、1和2个特征图卷积得到的;经C3层输出的第1个特征图,是由S2输出的6个特征图中的第1、2和3个特征图卷积得到的,依次类推······
为什么要对S2输出的特征图进行组合使用?——对不同的卷积核给予不同的输入,可以增强而后输出的特征图间的互补性,也就是让C3输出的特征图语义能够各有含义又相互补充。
4. S4:input_size = 16@10×10 ,output_size = 16@5×5
S4层池化层大小为2×2,池化过程同S2层。
5. C5:input_size = 16@5×5 ,output_size = 120@1×1
C5层的卷积核数目为120,大小同C3层(为5×5),但卷积操作不同于C3,C5层卷积时同时使用了S4输出的16个特征图。
那么,你可能会有疑惑——卷积核大小和input进来的特征图大小一样,这不就等价于全连接操作吗?那为什么要叫卷积层?
确实,在这里看来,C5的操作就是全连接操作。那么,为什么还要叫其卷积层呢?原因在于如果此时网络的输入图像input要比32×32大的话,S4层得到的特征图就不是5×5大小,自然C5层输出的特征图也不再是1×1大小了,可能是2×2大小、3×3大小······那么,此时自然不可称其为全连接层。
6. F6:input_size = 120 ,output_size = 84
F6层是全连接层,用84个神经元去进行全连接操作,得到size为84的vector。
7. OUTPUT:input_size = 84 ,output_size = 10
OUTPUT层,即输出层,经由RBF函数输出分类结果(手写数字为0-9,共10个数字,所以最后输出的类别数目是10),RBF函数输出的值越大,表示input是该类别的可能性越小。也就是说,input经LeNet分类后,得到的分类结果是RBF函数最小输出值所对应的类别(这和Softmax正好相反)。
- RBF函数:
y i = ∑ j ( x j − w i j ) 2 y_i=\sum\limits_{j}(x_j-w_{ij})^2 yi=j∑(xj−wij)2
以上就是LeNet的核心内容,更细节的知识可点击文章顶部的原论文链接作进一步了解。
模型部分代码:
import torch
import torch.nn as nn
class LeModel(nn.Module):
def __init__(self, num_class=10):
super(LeModel, self).__init__()
self.conv1 = nn.Conv2d(1, 6, 5) # 1x28x28 -> 6x24x24
self.pool1 = nn.AvgPool2d(2) # 6x24x24 -> 6x12x12
self.conv2 = nn.Conv2d(6, 16, 5) # 6x12x12 -> 16x8x8
self.pool2 = nn.AvgPool2d(2) # 16x8x8 -> 16x4x4
self.conv3 = nn.Conv2d(16, 120, 4) # LeNet的input是32x32,MNIST为28x28,对此修改卷积核尺寸为4x4
self.FC1 = nn.Linear(120*1*1, 84)
self.Classifier = nn.Linear(84, num_class)
def forward(self, x):
x = torch.tanh(self.conv1(x))
x = self.pool1(x)
x = torch.tanh(self.conv2(x))
x = self.pool2(x)
x = torch.tanh(self.conv3(x))
x = x.view(-1, 120*1*1)
x = self.FC1(x)
x = torch.tanh(x)
x = self.Classifier(x)
return x
module name input shape output shape params memory(MB) MAdd Flops MemRead(B) MemWrite(B) duration[%] MemR+W(B)
0 conv1 1 28 28 6 24 24 156.0 0.01 172,800.0 89,856.0 3760.0 13824.0 66.68% 17584.0
1 pool1 6 24 24 6 12 12 0.0 0.00 3,456.0 3,456.0 13824.0 3456.0 0.00% 17280.0
2 conv2 6 12 12 16 8 8 2416.0 0.00 307,200.0 154,624.0 13120.0 4096.0 0.00% 17216.0
3 pool2 16 8 8 16 4 4 0.0 0.00 1,024.0 1,024.0 4096.0 1024.0 0.00% 5120.0
4 conv3 16 4 4 120 1 1 30840.0 0.00 61,440.0 30,840.0 124384.0 480.0 16.66% 124864.0
5 FC1 120 84 10164.0 0.00 20,076.0 10,080.0 41136.0 336.0 16.66% 41472.0
6 Classifier 84 10 850.0 0.00 1,670.0 840.0 3736.0 40.0 0.00% 3776.0
total 44426.0 0.02 567,666.0 290,720.0 3736.0 40.0 100.00% 227312.0
=====================================================================================================================================
Total params: 44,426
-------------------------------------------------------------------------------------------------------------------------------------
Total memory: 0.02MB
Total MAdd: 567.67KMAdd
Total Flops: 290.72KFlops
Total MemR+W: 221.98KB
实现部分:
import torch
import torch.optim as optim
from LeNet import LeModel
import torchvision.transforms as transforms
from torchvision.datasets import MNIST
import torch.utils.data
import torch.nn as nn
def main():
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(f'device is {device}')
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize(0.5, 0.5)])
train_data = MNIST(root='./data', train=True,
transform=transform, download=False)
train_loader = torch.utils.data.DataLoader(train_data, batch_size=16, shuffle=True)
test_data = MNIST(root='./data', train=False,
transform=transform, download=False)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=16, shuffle=True)
net = LeModel()
net.to(device)
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.5)
loss_function = nn.CrossEntropyLoss()
net.train()
for epoch in range(10):
running_loss = 0.0
for step, (images, labels) in enumerate(train_loader, start=0):
optimizer.zero_grad()
images, labels = images.to(device), labels.to(device)
output = net(images)
loss = loss_function(output, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if step % 500 == 499:
print('epoch: %d | step: %5d | train_loss: %.5f |' % (epoch+1, step+1, running_loss/500))
running_loss = 0.0
print('Finished Training !')
net.eval()
correct = 0
total = 0
with torch.no_grad():
for images, labels in test_loader:
images, labels = images.to(device), labels.to(device)
output = net(images)
_, predict = torch.max(output.data, 1)
total += labels.size(0)
correct += (predict == labels).sum().item()
print('Accuracy of the network on the 10000 test images: %d %%' % (
100 * correct / total))
if __name__ == "__main__":
main()
实现结果:
device is cuda
epoch: 1 | step: 500 | train_loss: 2.28888 |
epoch: 1 | step: 1000 | train_loss: 2.23163 |
epoch: 1 | step: 1500 | train_loss: 2.11627 |
epoch: 1 | step: 2000 | train_loss: 1.86734 |
epoch: 1 | step: 2500 | train_loss: 1.52226 |
epoch: 1 | step: 3000 | train_loss: 1.23563 |
epoch: 1 | step: 3500 | train_loss: 1.01717 |
epoch: 2 | step: 500 | train_loss: 0.83994 |
epoch: 2 | step: 1000 | train_loss: 0.74169 |
epoch: 2 | step: 1500 | train_loss: 0.67354 |
epoch: 2 | step: 2000 | train_loss: 0.61439 |
epoch: 2 | step: 2500 | train_loss: 0.56078 |
epoch: 2 | step: 3000 | train_loss: 0.53076 |
epoch: 2 | step: 3500 | train_loss: 0.50286 |
epoch: 3 | step: 500 | train_loss: 0.48683 |
epoch: 3 | step: 1000 | train_loss: 0.44536 |
epoch: 3 | step: 1500 | train_loss: 0.43714 |
epoch: 3 | step: 2000 | train_loss: 0.43089 |
epoch: 3 | step: 2500 | train_loss: 0.39770 |
epoch: 3 | step: 3000 | train_loss: 0.38524 |
epoch: 3 | step: 3500 | train_loss: 0.38559 |
epoch: 4 | step: 500 | train_loss: 0.36031 |
epoch: 4 | step: 1000 | train_loss: 0.35656 |
epoch: 4 | step: 1500 | train_loss: 0.35450 |
epoch: 4 | step: 2000 | train_loss: 0.33272 |
epoch: 4 | step: 2500 | train_loss: 0.33033 |
epoch: 4 | step: 3000 | train_loss: 0.33187 |
epoch: 4 | step: 3500 | train_loss: 0.32718 |
epoch: 5 | step: 500 | train_loss: 0.31304 |
epoch: 5 | step: 1000 | train_loss: 0.29062 |
epoch: 5 | step: 1500 | train_loss: 0.29978 |
epoch: 5 | step: 2000 | train_loss: 0.28638 |
epoch: 5 | step: 2500 | train_loss: 0.29343 |
epoch: 5 | step: 3000 | train_loss: 0.28156 |
epoch: 5 | step: 3500 | train_loss: 0.26574 |
epoch: 6 | step: 500 | train_loss: 0.25187 |
epoch: 6 | step: 1000 | train_loss: 0.25617 |
epoch: 6 | step: 1500 | train_loss: 0.25704 |
epoch: 6 | step: 2000 | train_loss: 0.25702 |
epoch: 6 | step: 2500 | train_loss: 0.25900 |
epoch: 6 | step: 3000 | train_loss: 0.23853 |
epoch: 6 | step: 3500 | train_loss: 0.23782 |
epoch: 7 | step: 500 | train_loss: 0.24016 |
epoch: 7 | step: 1000 | train_loss: 0.22873 |
epoch: 7 | step: 1500 | train_loss: 0.21722 |
epoch: 7 | step: 2000 | train_loss: 0.21353 |
epoch: 7 | step: 2500 | train_loss: 0.21186 |
epoch: 7 | step: 3000 | train_loss: 0.22035 |
epoch: 7 | step: 3500 | train_loss: 0.20373 |
epoch: 8 | step: 500 | train_loss: 0.20141 |
epoch: 8 | step: 1000 | train_loss: 0.18840 |
epoch: 8 | step: 1500 | train_loss: 0.19219 |
epoch: 8 | step: 2000 | train_loss: 0.19408 |
epoch: 8 | step: 2500 | train_loss: 0.19582 |
epoch: 8 | step: 3000 | train_loss: 0.18561 |
epoch: 8 | step: 3500 | train_loss: 0.19368 |
epoch: 9 | step: 500 | train_loss: 0.17709 |
epoch: 9 | step: 1000 | train_loss: 0.16726 |
epoch: 9 | step: 1500 | train_loss: 0.18412 |
epoch: 9 | step: 2000 | train_loss: 0.16990 |
epoch: 9 | step: 2500 | train_loss: 0.16549 |
epoch: 9 | step: 3000 | train_loss: 0.17277 |
epoch: 9 | step: 3500 | train_loss: 0.16431 |
epoch: 10 | step: 500 | train_loss: 0.16025 |
epoch: 10 | step: 1000 | train_loss: 0.16447 |
epoch: 10 | step: 1500 | train_loss: 0.15842 |
epoch: 10 | step: 2000 | train_loss: 0.14480 |
epoch: 10 | step: 2500 | train_loss: 0.15598 |
epoch: 10 | step: 3000 | train_loss: 0.14052 |
epoch: 10 | step: 3500 | train_loss: 0.15464 |
Finished Training !
Accuracy of the network on the 10000 test images: 96 %