GCN图卷积神经网络总结笔记
参考文章：一文读懂图卷积GCN - 知乎
Graph Neural Network（GNN）
图神经网络(Graph Neural Network, GNN)是指神经网络在图上应用的模型的统称。根据采用的技术不同和分类方法的不同，又可以分为不同种类，例如从传播的方式来看，图神经网络可以分为图卷积神经网络（GCN），图注意力网络（GAT，缩写为了跟GAN区分），Graph LSTM等等，本质上还是把文本图像的那一套网络结构技巧借鉴过来做了新的尝试。着重理解最经典和最有意义的基础模型GCN，这也是理解其他模型的基础。
Graph Convolutional Network（GCN）
图卷积神经网络GCN属于图神经网络GNN的一类，是采用卷积操作的图神经网络。图上的卷积网络从卷积方式上可以分为两种：1.谱（spectral）卷积，2.空间域卷积。GCN属于谱卷积，即将卷积网络的滤波器与图信号同时搬移到傅里叶域以后进行处理。
GCN，实际上跟CNN的作用一样，就是一个特征提取器，只不过它的对象是图数据。GCN精妙地设计了一种从图数据中提取特征的方法，从而让我们可以使用这些特征去对图数据进行节点分类、图分类、边预测，还可以顺便得到图的嵌入表示，用途广泛。
卷积VS图卷积
卷积：用随机的共享的卷积核得到像素点的加权和从而提取到某种特定的特征，然后用反向传播来优化卷积核参数就可以自动的提取特征，是CNN特征提取的基石。但是，存在很多CNN、RNN无法解决或者效果不好的问题——图结构的数据。
图卷积：现实中更多重要的数据集都是用图的形式存储的，这些图网络的形式并不像图像，是排列整齐的矩阵形式，而是非结构化的信息，那有没有类似图像领域的卷积一样，有一个通用的范式来进行图特征的抽取呢？这就是图卷积在图卷积网络中的意义。对于大多数图模型，有一种类似通式的存在，这些模型统称GCNs。因此可以说，图卷积是处理非结构化数据的大利器。
理解图卷积
图中的每个结点无时无刻不因为邻居和更远的点的影响而在改变着自己的状态直到最终的平衡，关系越亲近的邻居影响越大。
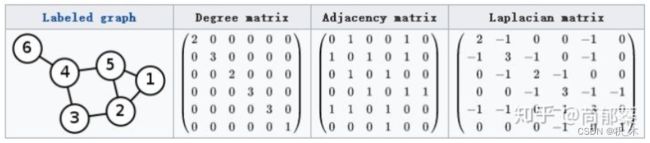
图相关矩阵：度矩阵(D)、邻接矩阵(A)、拉普拉斯矩阵(L) 【此处L为 D - A 】
图卷积通式：
图卷积通式实现
几种具体的实现，但是每一种实现的参数大家都统称拉普拉斯矩阵。
实现一
思路：基于节点特征与其所有邻居节点有关的思想。邻接矩阵A与特征H相乘，等价于，某节点的邻居节点的特征相加。这样多层隐含层叠加，能利用多层邻居的信息。
存在问题：
- 没有考虑节点自身对自己的影响；
- 邻接矩阵A没有被规范化，这在提取图特征时可能存在问题，比如邻居节点多的节点倾向于有更大的影响力。
实现二（针对问题一改进）
拉普拉斯矩阵 L= D - A ，引入了度矩阵，从而解决了没有考虑自身节点信息自传递的问题
实现三（主流）
- 引入自身度矩阵，解决自传递问题；
- 对邻接矩阵的归一化操作，通过对邻接矩阵两边乘以节点的度开方然后取逆得到。
具体到每一个节点对 i，j ，矩阵中的元素由下面的式子给出（对于无向无权图）
【提示：对于单个节点运算来说，做归一化就是除以它节点的度，这样每一条邻接边信息传递的值就被规范化了，不会因为某一个节点有10条边而另一个只有1条边导致前者的影响力比后者大，因为做完归一化前者的权重只有0.1了，从单个节点上升到二维矩阵的运算，就是对矩阵求逆了，乘以矩阵的逆的本质，就是做矩阵除法完成归一化。左右分别乘以节点i,j度的开方，就是考虑一条边的两边的点的度。】
从思考角度不同，可以这样理解：对于单个节点就是除法，对于矩阵就是乘以度矩阵的逆。
GCN具体形式
模型输入：特征矩阵X、邻接矩阵A (变形过的
)
模型深入：上一层的输出、邻接矩阵A (变形过的
)
特征矩阵：图数据中有N个节点（node），每个节点都有自己的特征，我们设这些节点的特征组成一个N×D维的矩阵X。
邻接矩阵：图数据中有N个节点之间的关系形成一个的N×N维矩阵A。
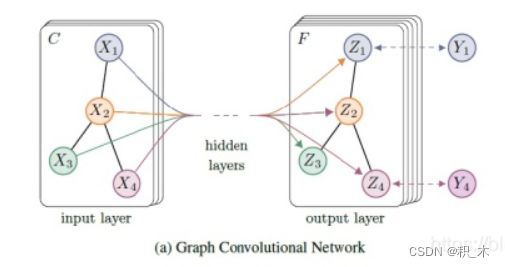
上图中的GCN输入一个图，通过若干层GCN每个node的特征从X变成了Z，但是，无论中间有多少层，node之间的连接关系，即A，都是共享的。（公式中，每层变换都有不变的A）
示例：训练一个node classification模型
1.假设构造两层的GCN，激活函数分别采用ReLU和Softmax，则整体的正向传播的公式为：
2.针对所有带标签的节点计算cross entropy损失函数
即使只有很少的node有标签也能训练，作者称他们的方法为半监督分类。
基于numpy设计的GCN网络参考代码
参考文章： 图卷积神经网络(GCN)_lamusique的博客-CSDN博客_图卷积神经网络