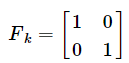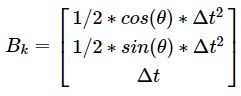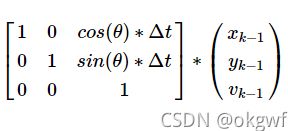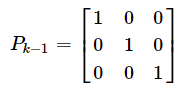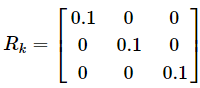一. 卡尔曼滤波器开发实践之一: 五大公式详解

       既然标题名称是开发实践,本系列文章将主要介绍如何在工程实践中使用卡尔曼滤波器,至于卡尔曼滤波器的五大公式如何推导而来,网上有很多大拿们写的都很精彩,这里不再叙述.可以参考了下面两篇博文:

1. 卡尔曼滤波器推导与解析 - 案例与图片

2. 扩展卡尔曼滤波新手教程

3. 代码参考: The Extended Kalman Filter: An Interactive Tutorial for Non-Experts 的作者放在github上的TinyEKF

这个系列计划分七小节介绍:

一.卡尔曼滤波器开发实践之一: 五大公式    也就是本文

二.卡尔曼滤波器开发实践之二:  一个简单的位置估计卡尔曼滤波器    

三.卡尔曼滤波器(EKF)开发实践之三:  基于三个传感器的海拔高度数据融合

四.卡尔曼滤波器(EKF)开发实践之四:  ROS系统位姿估计包robot_pose_ekf详解

五.卡尔曼滤波器(EKF)开发实践之五:  编写自己的EKF替换robot_pose_ekf中EKF滤波器

六.卡尔曼滤波器(UKF)开发实践之六: 无损卡尔曼滤波器(UKF)进阶-白话讲解篇

七.卡尔曼滤波器(UKF)开发实践之七: 无损卡尔曼滤波器(UKF)进阶-实例篇

-------------------------------------------正文开始---------------------------

一. 卡尔曼滤波器的两大步骤和五大公式

预测步骤:

<1>  

<2>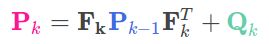   

更新步骤:

<3>     

<4>   

<5>   

 二. 公式<1>:

 1. 和

     和数据类型相同, 均表示系统状态值向量,一般就是你的系统想要的输出结果集或中间值集. 系统状态值是个n维列向量(你称它为nx1矩阵也可),形式如:

 或

向量的维数n就是系统状态值个数(n>=1).  确定好并记住的这个维数n,后面公式很多矩阵会用到.

        举例说明, 你要用卡尔曼滤波器估计一个圆点跟随鼠标在屏幕上的移动位置,这个状态向量就要定义为一个2维列向量(x   y). 再比如你要融合3路传感器读数为一个最优读数,状态向量就是个1维列向量( x ).

         表示系统初始状态值(滤波器初始化时设置)或上一时刻状态值, 当表示上一时刻状态值时,它一般就是上一次执行预测和更新步骤后,公式<4>的结果,即上次预测和更新的最优估计值: .

        是一次完整的预测和更新步骤的系统中间状态值,是基于做公式<1>运算后的结果向量值,当然类型也同.   

        记住,如果要设置系统初始状态,我们设置的是,不是.  程序运行周期执行预测和更新公式时,最后的最优估计值,会再次设置到进行新一轮预测更新计算. 

2. 

       这是一个根据你的系统状态变换方程得到的状态转移矩阵,也叫预测矩阵.  之所以叫状态转移矩阵,是因为它反应的是: 当测量值未介入计算时,前后两个时刻的状态值变化情况. 之所以又叫预测矩阵, 可以理解为在预测公式<1>中根据上一时刻系统状态预测(计算)出当前时刻系统状态.

        那么,系统状态变换方程又是什么?怎么求? 

      预测矩阵一定是一个nxn的矩阵,只有这样才能保证矩阵和列向量乘法:  F_k(nxn) * X_k-1(n*1) = X_k(nx1) 结果还是个n维列向量,即: ,  后边同理,它非必须有,取决于你的系统状态如何变化,如果有,需要保证其结果是一个n维列向量,这个后面再说.

        那么(nxn)矩阵如何设置呢?  取决于你的系系统状态变换方程. 还是直接举例. 

        (1) 假如用卡尔曼滤波器估计一个圆点跟随鼠标在屏幕上的位置Point(x,y),系统状态值是一个2维向量(x  y). 如果当前鼠标位置Point(x,y)作为测量值还未参与计算时(公式<4>才参与), 前后时刻系统状态向量(x  y)保持不变,即=,即:  x_k = x_k-1 + 0,   y_k = 0 + y_k-1.  这个就是系统状态变换方程.  而反应这种系统状态变换方程的状态转移矩阵(2x2)就是:

  进一步: (暂不考虑)

  此时:  = 

        (2) 假如一个把3路传感器读数融合为一个最优读数的系统,系统状态值是一个1维向量(x),  在新的3路传感器读数参与到公式<4>之前,前后时刻系统状态变换方程也是恒等关系,不会变化.

(1x1)就是: 

             ,  是个1x1矩阵. 进一步:  

        (3) 再一个复杂点的例子. 你的系统要评估一个直线匀速运动的小车在平面地图上的位置Position(x,y), 匀速速度为v=2 pixel/s.也就是系统状态为3维列向量(x  y  v )或写作[x  y  v]. 直线运动方向固定为θ=30°. 我们看看这个系统状态变换方程:

根据初中物理运动学公式:  St = S0 + v * t  有:

x轴方向新位置x:  x_k = x_k-1    +       0         +    cos(θ) * v_k-1 * Δt

y轴方向新位置y:  y_k =    0        +    y_k-1     +   sin(θ) * v_k-1 * Δt

直线运动速度v:    v_k =    0        +       0         +    v_k-1

 Δt为每次预测和更新调用时间周期T.

用矩阵表示就是(3x3):      进一步: 

 Note: 这里要注意一点时. 我们固定了小车运动方向θ=30°, cos(θ)和sin(θ)计算结果是固定值. 所以小车的系统状态变化符合线性计算,符合高斯分布计算.   假如小车运动方向θ非固定随时可变化.  小车可以左右随意转向, 小车的系统状态变化呈非线性,不再符合高斯分布, 那么现在的定义形式就不再适用了.  这种情况应该是一个3x3雅各比矩阵形式.  这个后面几个小节会详细说明,可以先理解下雅各比矩阵概念.

        另外,这里讲的线性和非线性,不是表面上小车是否沿直线运动,  而是因为cos(θ)和sin(θ)两个三角函数,当θ变化时,其图形是曲线,变化率不固定.

3.  

        : 系统控制矩阵,具体结构和取值由实际系统控制逻辑决定.

          : 系统控制向量, 由外部对系统控制信号决定. 可以是单变量(1维向量)或n维向量.

         大多数卡尔曼滤波系统中 并不是必须的,这由你的具体系统决定. 如果需要用到, 从公式<1>的形式上可以看出,的结果也必定是一个和,结构一样的n维列向量,以保证和前面的结果向量相加.  这也就决定了和的结构形式.一般组合为(矩阵和向量乘法): 

[nxn] * (nx1)  = (nx1)  或  [nx1] * u = (nx1)

        我们继续以上面例子(3)来介绍. 在上面列子基础上, 我们加入加速速(踩提速油门))和减速(刹车)控制, 也就是物理运动学中的加速度a, a > 0 是加速,a < 0时减速, a = 0时匀速或静止.  那具体怎么放入呢? 

        同样需要做运动学方程分析, 根据初中物理运动公式: 

        v_t = v_0 + a * Δt 

        S_t = S_0  +  v_0* Δt +  1/2 * a *    

于是上面例子(3)的状态方程改为:

x轴方向新位置x:  x_k = x_k-1    +       0         +    cos(θ) * v_k-1 * Δt      +    1/2 * cos(θ) * a *   

y轴方向新位置y:  y_k =    0        +    y_k-1     +   sin(θ) * v_k-1 * Δt        +    1/2  * sin(θ) * a *   

直线运动速度v:    v_k =    0        +       0         +    v_k-1                          +     a * Δt 

这三个式子中,前4部分保持不变,最后1项,从列方向单列出就是:

 ​​      

至此,完整的公式<1>就是:

 三. 公式<2>: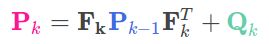  

         有了公式<1>的预测公式实现,  公式<2>的实现就简单了. 至于公式<2>的理论依据,不是本文重点,请参考五大公式理论推导. 本文只关注开发实践.

         : 前面有了的实现,只是的转置矩阵. 

        和 : 一般定义是: 针对系统状态列向量或的系统不确定性协方差矩阵. 由此可以确定和的结构为nxn的矩阵(方阵).   结构有了,可怎么设置该矩阵各元素的取值? 

        我们先回忆下协方差的概念和用途:   

        在概率论和统计学中协方差用于衡量两个变量(x和y)的总体误差。协方差表示的是两个变量的总体的误差，如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

        从数值上来看,协方差数值越大,两个变量同向的程度越大,反之亦然.

        而方差是协方差的一种特殊情况，即当两个变量是同一变量(x和x)。我们知道方差它反映的是数据序列与均值的关系。 

        所以,对于nxn的协方差矩阵,把系统状态列向量的各个元素看做均值, 对角线(左上到右下)上的元素就是各个元素的方差, 这个对角线方差(i,i)表示偏离均值的大小关系. 比如针对上面小车直线运动例子:(1,1)表方差Variance(x),(2,2)表方差Variance(y),(3,3)表方差Variance(v).  除对角线以外的元素表示系统状态列向量各元素除自身对自身之外,相互之间的协方差. 如: Cov(x,y)表x坐标分量和y坐标分量的协方差.Cov(x,v)表x坐标分量和速度v之间的协方差.Cov(x,y)的意义不明显. 但Cov(x,v)和Cov(y,v)则表示速度v分量对x坐标分量或y坐标分量的影响. 因为v的大小,会直接影响x坐标或y坐标的状态变化尺度. 讲这些,就是为了说明协方差矩阵是如何表示和影响系统状态变化的.   

        好了. 现在我们来设置(同系统状态向量,设置协方差矩阵初始值,我们设置,而不是,只是公式计算过程中间值.),其实主要是设置对角线上的元素值. 如果你认为系统状态初始值的值很准确, 很可靠,可信赖,那么对应的(i,i)就应该是比较小的值(因为对角线是方差,方差越小表示越准确);  如果系统状态初始值的无法确定,你初始设置了一个自己都感觉很不靠谱的值,  那么对应的(i,i)就应该是比较大的值(因为对角线是方差,方差越大表示误差越大);   注:  这里是开发实践中的个人理解,如有更好的解释,欢迎提出建议.

        同样用上面例子(3)小车直线运动的例子,系统初始状态值一般通过小车的传感器都能轻松获取到,而且误差不会太大,较可信.  我们可以设置为: 

      是计算过程中间值,我们可以不用管. 程序运行周期执行预测和更新公式时,最后的最优估计协方差矩阵,会再次设置到进行新一轮预测更新计算.

        : 称为噪声协方差矩阵. 再精密的硬件设计和系统软件设计,都无法做到100%精准,终会有误差,甚至无法用数学表达,我们把这些系统或世界中无法表达且会对系统状态变量带来不确定性的影响视作噪声.

        同上面一样,也是个nxn矩阵, 有效元素一般为对角线元素, 这种噪声一般都很小,所以对角线元素一般设置很小的值即可,比如小数点后4位以后的浮点数. 一个例子:

四. 公式<3> : 

        : 称为卡尔曼增益. 它的来历是卡尔曼滤波器公式推导过程中, 两个高斯曲线方程相乘后,求得一个新的高斯曲线方程, 得到的新的均值和新的方差,并经过合并同类项,提取公因式等操作,提取到的一个公共因数. 

        所以,开发实践中, 这个公式除了和外, 我们不必过多关注,只要要找公式定义编写代码即可.

         : 即的转置矩阵, 这个我们放到公式<4>中讲解.

        : 传感器噪声协方差矩阵, 其矩阵尺寸要注意.  因为是针对各个传感器的测量值的,所以其矩阵尺寸是传感器测量值个数m. 即mxm方阵.  同样其有效值一般也是设置对角线元素, 具体设置需要参考传感器手册,一般都有说明.  实在不行,自己依据经验主观设置逐渐尝试也可以.

        以上面例子(3)小车直线运动的例子,测量值和状态值一样,都是3维列向量(    ),则有:

五. 公式<4> : 

         :  本次预测更新的系统状态向量的最优估计值, 作为程序输出结果使用, 并作为下一次预测的估计初始值赋值给.

         : 系统传感器观测值或测量值m维列向量(m)或矩阵(mxm).  m为输入系统的传感器变量个数. m>0,因为总要有个测量值.

        针对上面例子(1): m=2,

        例子(2):m=3,

        例子(3): m=3  

        :   这个很重要,和一样重要!!!!!!!!

        其名称各个版本说法不一.  我的理解是:  是把当前预测阶段输出的先验估计值列向量(nx1)的各个状态值转换为和传感器测量列向量(mx1)的对应测量值同一尺度,同一单位,或同一度量的转换函数或映射关系.    读起来多少有点绕口. 

        Note: 有效值一般也为对角线元素.

        当这个映射关系为恒等关系时,   对应元素取值为1;

        当这个映射关系为线性变换关系时,   对应元素取值类似于ax+b的直线方程式;

        但当这个映射关系为非线性关系时,  应该是个雅各比矩阵. 不错! 又是它, 这个货再次出现. 这个雅各比矩阵的对应元素,将完成非线性到线性的转换.

        在Note一下:  如果和处理的都是线性关系,那么就是卡尔曼滤波器;  如果和有至少一个处理了非线性转线性关系,也就是说用到了雅各比矩阵,那么就升级为扩展的卡尔曼滤波器,即:EKF.

       说了一大堆究竟如何设置呢?  我们先说它的矩阵结构.从公式<4>中可以看出

的计算结果要从做减法.  是m维列向量,所以结果也应该是个m维列向量.  我们已知是个n维列向量.  由:

  可知: 为mxn矩阵.

        为mxn矩阵. 为mxn矩阵. 为mxn矩阵.  重要的事情讲3遍.

        下面介绍下的元素怎么设置取值.:

        对于明显的线性转换关系, 的设置比较简单, 1比1恒等,对角线就设置为1,这种情况比较多,大多数都是恒等关系直接置1即可,比如: n=3,m=3时;

,    为一个固定值矩阵.

        对于非恒等关系的线性关系,如:z=ax+b,比如: n=3,m=3时,假如所有状态量均为同一线性关系:

可见这里为一个动态值矩阵,需要每次根据的各个状态分量去动态设置.

        对于非线性关系,需要做线性化处理.  这就用到高中导数和导函数知识.复习一下

 

这里插播一下.   我们回想前面二. 公式<1>中讲解时,举例3中匀速直线运动的小车,因为小车运动方向θ=30°是个固定值.  它的设置直接使用了cos(θ)和sin(θ)形式.  如果小车运动方向θ随时可变,呈非线性. 我们就要使用cos函数的导函数: -sin(θ), sin函数的导函数: cos(θ),分别代替中的cos(θ)和sin(θ)  此时就成为了一个雅各比矩阵.

         如果对于一个非线性关系,你不会或无法求出其导函数或偏导函数. 可以直接按照导数的物理意义或几何意义所描述那样, 直接使用其有限差分或连续差分代替. 公式就是上面引用的导数的几何意义,曲线的任一点切线斜率公式:

 用这个公式,设置中非线性关系元素.可见这里是一个动态的雅各比矩阵,需要根据本次和上次的各个状态分量以及其对应本次和上次计算出的经连续差分公式计算后,去动态设置:

六. 公式<5> : 

        终于到最后一个公式:  

其实它还可以进一步提取公因式后,精简为: 

这个在编写程序时可以使用.

        : 同类似, 为本次预测更新后获得的最优协方差矩阵.  作为程序输出结果使用, 并作为下一次预测的协方差矩阵赋值给. 做下一次预测和更新.

        这个公式<5>,没有其他可说的, 按照公式编写代码即可.

七. 总结: 

        本来想介绍下卡尔曼滤波器五大公式在开发实践中的用法,没想到竟然写这么多.   开始有点担心会不会有人认真看完了.