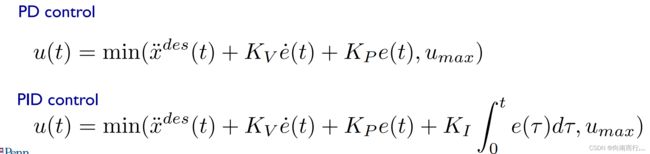Robotics: Aerial Robotics（空中机器人）笔记（二）:如何设计一架四旋翼无人机
在这一章里，我们将探索四旋翼如何飞行的。 这章将会讲一些基本的力学原理以及如何设计无人机。
上一章链接：
Robotics: Aerial Robotics（空中机器人）笔记（一）： Introduction
基本的力学原理（Basic Mechanics）
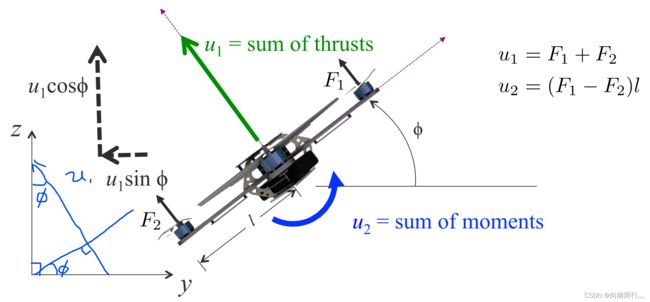
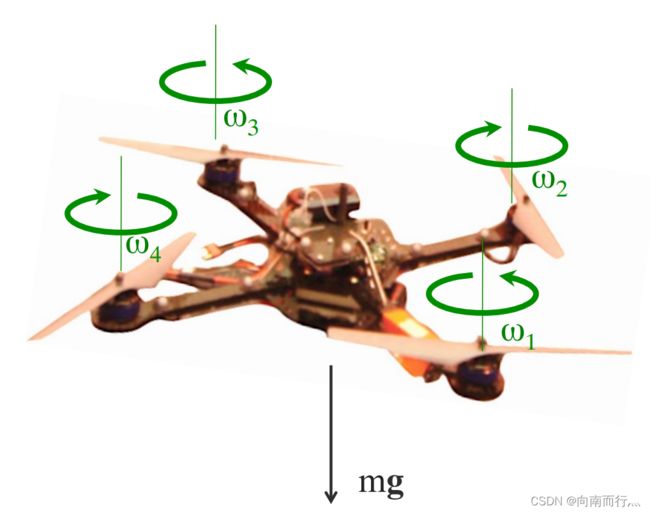
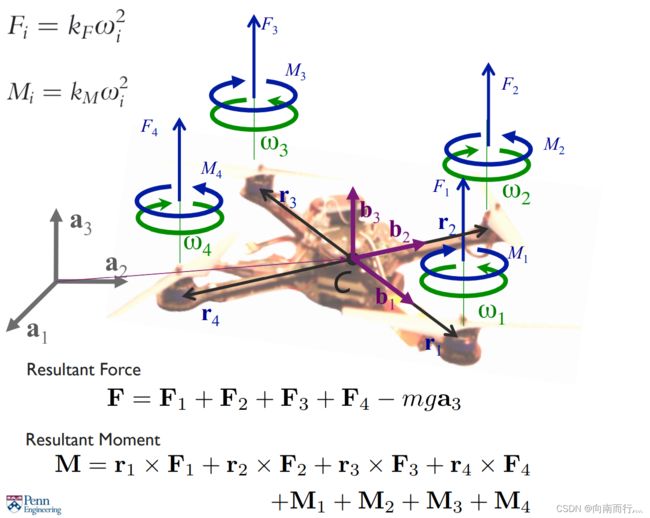
一个四旋翼有四个电机来支持飞行器的重量
，每个电机会旋转并产生一个向上推力，与此同时，电机的旋转需要克服阻力矩，所以我们需要观察推力和阻力矩这两个量与电机转速的关系。
这里不太清楚力矩的概念的话可以看下这里：
作者：一根儿芦苇
链接：https://www.zhihu.com/question/20260034/answer/287592720
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
研究一种物理现象的时候，我们希望能找出来影响它的因素，然后再将这些因素量化，进而总结出规律，得出它们和现象之间的关系。
比如我们推地面上的一箱东西，到底用多大的力才能推动呢？
通过实验观察我们发现箱子越重，越难推动。还有就是地面越粗糙，越难推动。也就是所，对于推箱子这件事儿，影响的因素有两个，一个是箱子本身的重量M，一个是地面的粗糙程度。这里遇到一个问题，就是粗糙程度该怎么表示，我们就想办法将它量化成一个系数k，叫做摩擦系数，地面越粗糙，k越大。那么推动箱子需要的力：
F=kM
这样就找到了推箱子需要的力。以后对于任何重量的箱子，在任何地面上，只要知道摩擦系数k，我们都可以用这个公式来计算出来推动它所需的力。
力矩类似。我们在转动一个东西时，比如用扳手拧螺丝。通过实验我们发现，要想拧动螺丝，一个是用的力越大越好，另一个就是扳手越长越好。也就是影响螺丝是否能被拧动的因素有两个，一个是扭力F，一个是力臂长度L，也就是扳手长度。如何来表示这种拧的作用的效果呢？也就是如何来量化这种作用？于是就有了扭矩，用公式表示为：
M = F X L
这里三个量都是向量，之所以用叉乘表示，是因为叉乘的这种运算正好和这种物理现象相吻合了。也就是力矩大小不仅和力F、力臂L的大小有关，还和二者的夹角有关。力矩的方向垂直于力和力臂所在的平面。
如果我们绘制出推力与电机转速的关系图：
我们可以看到， 推力
和阻力矩
与转速的关系都可以看作一个二次方程，这里的k是一个系数，相当于我们求平推一个物体产生的摩擦力时地面的摩擦系数。
通过观察推力与转速的关系曲线，可以确定要求产生等于四分之一重量推力的转速
，同时这需要克服相应的阻力矩，那么我们怎么克服呢？通过调整电机的尺寸，电机可产生扭矩来克服前述的阻力矩，也就是图中这个
(描述电机扭矩与转速的关系曲线)。
所以说，如果我们要使四旋翼无人机处于悬停状态的话，产生的推力和扭矩就要满足以下公式：
当我们知道相应的系数
和
以及无人机的质心位置时，就能求出对应的合力以及合力矩了，其中r是质心到每个转子的距离。
在平衡状态时，合力明显为零，而合力矩也是零。
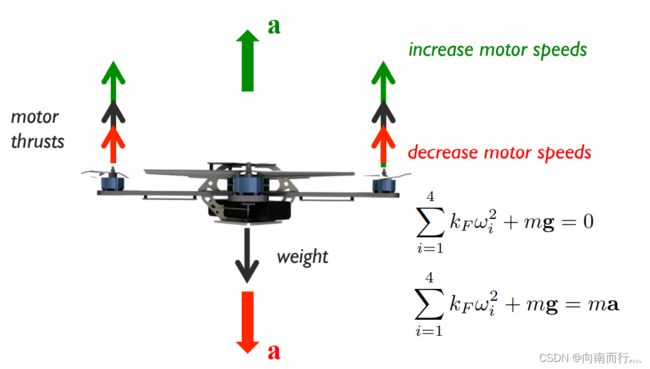
但是当合力在瞬时非零时， 会发生什么呢？ 其会得到加速度。简单起见我们先说垂直方向的加速度，当转子的推力之和（主要是转子的转速决定）大于四旋翼的重量时，会产生向上的加速度，反之则产生向下的加速度，式子如下所示：
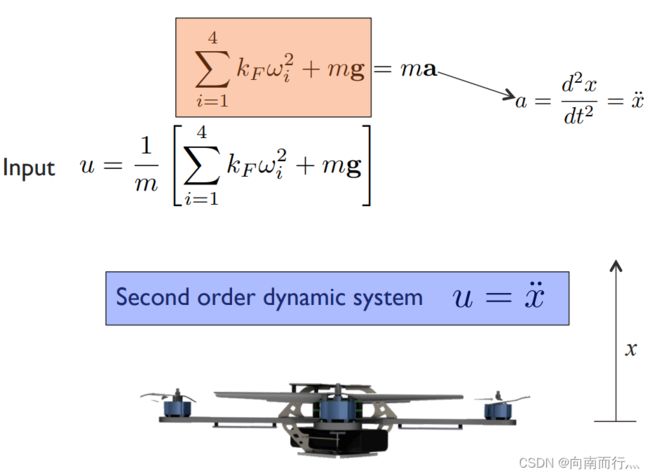
动力学与一维线性控制（Dynamics and 1-D Linear Control）
这一部分主要还是讨论在垂直方向上的运动，我们的目的就是让控制四旋翼机器人达到一个要求的垂直高度，也就是需要往上或往下位移一段距离 
。
显然，我们可以通过位移的二阶导数来求出加速度：
我们用 u 来表示合力除以质量:
![u=\frac{1}{m}[\sum_{i=1}^{4}k_fw_{i}^2+m\textbf{g}]](http://img.e-com-net.com/image/info8/563b6ee957104d49a81b6ff65f6b4fd4.gif)
就能得到一个二阶微分方程:
我们控制这台四旋翼的目标其实就是确定函数 
进而四旋翼到达期望位置 。
正如上文所述，这是非常简单的一个二阶线性系统，我们找到输入 关于时间 
的函数
可以驱动 到达预期的位置 
。
为此定义了一个误差函数
，表示期望轨迹和实际的轨迹之间的误差量，
很明显误差越大 （系统）对实际轨迹的偏差就越大，我们要做的就是要消除误差至零，并且是指数地收敛到零（更快且更平稳），也就是找到 满足：
其中第一个式子就是让误差指数地收敛到零，具体怎么来的可以看下面的链接：
PD控制器的另一解释与应用
第二个式子的推导：
其中，
为微分增益（derivative gain），
为比例增益（proportional gain），
称为前馈项（feedforward term）。当 和 都为正时，就能保证误差项能以指数的速度趋向于零。
比例增益其越高， 系统变得更有弹性和更有可能超调。 比如说当前状态是2，期望状态是4，误差是2，当前比例增益的话可能调节量是+1，那么状态就变成3，误差为1，如果增加比例增益，那么调节量可能变成+2，误差就为0，如果再增加比例增益，调节量可能变成+3，误差就变-1，也就是超调了。
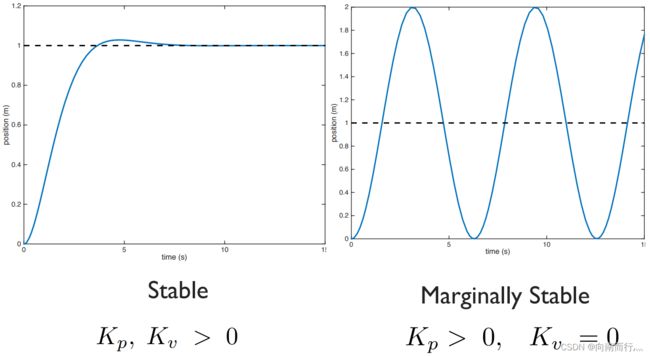
微分增益越高，系统本质上是加大了缓冲。 我们可以粗略理解这一项为能量衰减率，如果为0， > 0，系统就处于不断振荡的状态。通过增加微分增益，我们可以让系统收敛得更平稳。但如果微分增益过大，那么系统就处于欠阻尼的状态，系统会收敛地比较慢，但不会振动得厉害。
在特殊情况下， 你可以考虑使用更复杂的版本的PD控制，也就是PID控制。比如在不知道系统的具体模型或存在某些未知的干扰因素时，可以引入一个额外的正比于误差积分的项：
虽然引入这一项会使微分方程变成三阶，使得求解变得困难，但是这会使误差项最终变成零。
设计考量（Design Considerations）
推重比
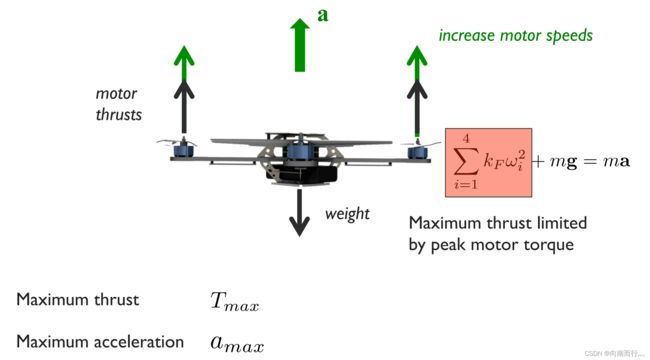
我们在之前的分析中总是假设电机能够产生控制器需要的推力，但是电机的推力是有限的，因为电机的转速会有一个峰值，这个峰值会导致四旋翼有一个最大的推力 
和最大的加速度 
。
我们在前面的式子就知道，控制输入 其实是由推力T和四旋翼的重力决定的，
假设你知道，通过简单地把最大推力和重量加起来，就可以得到 
：
所以现在当我们做 PD 控制和PID控制时, 还要由最大推力决定：
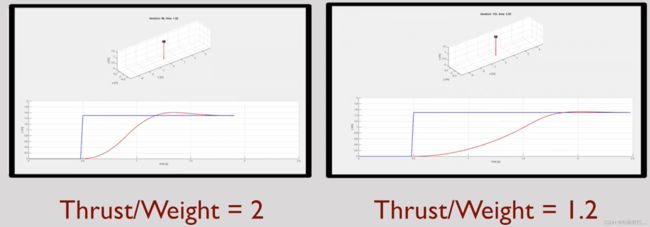
这个最大推力和重量的比例就是推重比 （thrust to weight ratio），我们可以通过调节推重比来调节四旋翼的控制性能。
能耗
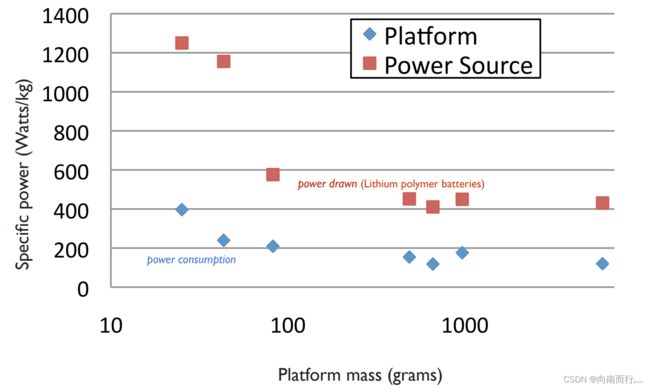
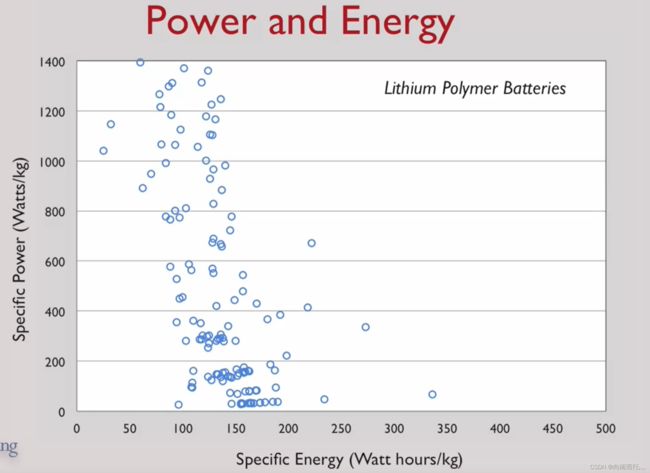
我们要让四旋翼飞起来，就要使得推力能产生足够的推力来抵抗重力。这就会产生基本功耗，四旋翼的基本功耗为：200 W/kg， 而所幸的是锂电池提供的能量基本 > 200 W/kg，所以实际上都能满足。
除了考虑功率消耗， 还需要考虑电池所携带的总能量，大多数的锂电池产生大约200 Whr/kg的电力：
现在用的最多的就是锂电池，但是现在锂电池并不携带大量的能量，那么我们如何让无人机飞得更久，通常就是减少重量。一般来说电池占总重的约35%， 电机加上螺旋桨占总质量的25%左右就可以了。
四旋翼携带的传感器也会消耗能量，通常来说它们因增加重量所消耗的能耗会比它们运作起来所消耗的能耗会大一些。
灵活性和可操作性（Agility and Maneuverability）
这一部分主要探讨如何使四旋翼能够灵活地移动。
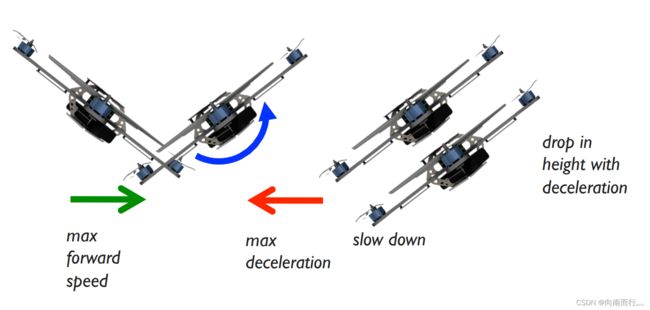
以最大速度停下（Maximum velocity to rest）
当四旋翼以最大速度向前飞行, 当你决定让它停到某个位置的时候， 你必须让它向后倾， 扭转推力方向， 这样才得以减速。但其结果是， 这会导致四旋翼的高度在垂直方向上降低， 因为垂直方向上的推力是小于现在的重量的。
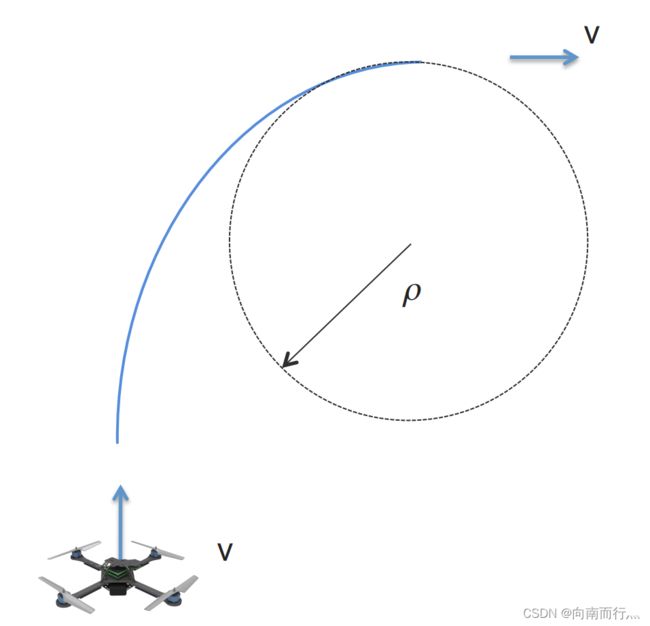
快速转弯且不减速 （Turn quickly without slowing down）
另一件是就是让四旋翼具备快速转弯的能力，目的是让四旋翼以最大速度向前飞行， 然后尽可能快速地转弯，主要通过减少转弯半径来实现。
运动分析
我们首先进行四旋翼以最大速度停下时的运动分析，以下图为例我们可以看到，此时四旋翼是倾斜的，而四旋翼转子所产生的推力是垂直于四旋翼的，所以我们将其合力与合力矩拆分成z轴和y轴两个方向，设四旋翼与y轴之间的夹角为 
, 就可以得到 
（注意它是有方向的）在z轴和y轴的分量分别是 
和 
（方向与运动方向相反，所以此时在减速）。
那么我们就能求得四旋翼在y轴，z轴的加速度以及角加速度：
同理 
（角加速度等于力矩除以转动惯量）
写成线性代数的形式就是：
我们想要更快地加减速，更快地旋转。就要：
最大化线性加速度 
：Maximize 
最大化角度加速度 
: Maximize 
部件选择（Component Selection）
由于我们想让无人机能够灵活地飞行，同时又要能实现一些功能（比如说自主飞行），那么我们就要搭载一些设备来完成这些功能。为此就要十分关注这些设备的重量（由上面的分析可知，重量也会影响飞行的灵活性），和功耗（功耗太大的话，就得考虑大电池，也会影响重量）。
尺寸的影响（Effects of Size）
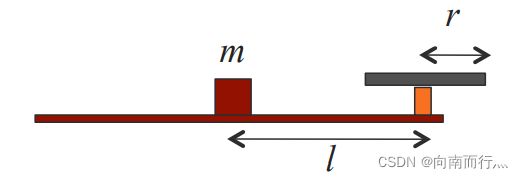
四旋翼的尺寸大小也会影响其灵活性，我们来看一个四旋翼的平面图，
是这个四旋翼的特征长度 （特征长度通常是指该物体长度中有代表意义的长度，是抽象出来的，这里可以粗略认为是四旋翼的尺寸），四旋翼的质量是 
，螺旋桨的半径是 
：
质量 正比于 的三次方（质量与体积相关，体积相当于长度乘三次），转动惯量正比于 的五次方（转动惯量等于质量乘以长度的平方）：
推力 
正比于螺旋桨转动的面积乘以转子叶尖线速度的平方：
力矩 
正比于推力乘以长度：
现在，假设桨叶大小与特征长度特征长度成正比 
，这个假设是满足几何约束的，所以有：
就有：
所以最大线加速度和最大角加速度会随着 和 
的变化而变化。
而其实 也是与 有关系的，在空气动力学中有两种缩放（scaling）。
Froude scaling ：
Mach scaling ：
所以基于这两种假设我们可以得到，四旋翼的尺寸越小，其能获得的最大角加速度就越大，也就越灵活。
下一章链接：
Robotics: Aerial Robotics（空中机器人）笔记（三）:无人机运动学