信息安全基础综合实验-基于中国剩余定理的秘密共享方案

最近没有什么事情，打算把之前的作业整理一下发出来，有需要的学弟学妹们可以参考一下。
相关：某电的密码学实验，信安专业必选实验

---

实验题目：基于中国剩余定理的秘密共享方案

实验目的

（包括实验环境、实现目标等等）
实验环境：
Windows 10
Visual studio 2017
Miracl库

实验目标：
1.通过算法编程，熟悉使用miracl库的基本函数操作
2.通过编程实现基于中国剩余定理的秘密共享方案，加深对于中国剩余定理的理解与运用
3.体会密码学与数论的紧密联系,将数论的知识运用于密码学的方案设计中
4.提高逻辑思维能力与实践能力

方案设计

2.1背景

2.2原理

2.3 算法步骤

方案实现

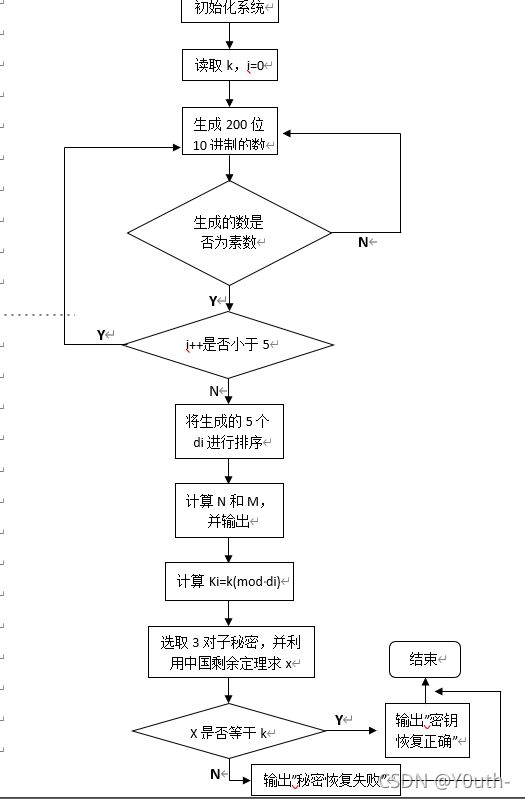
3.1 算法流程图

3.2 主要函数
（1）egcd()
函数原型：int egcd(x,y,z)
参数类型：big x,y,z;
功能：用来计算两个大数的最大公约数， 即z=gcd(x,y)。
（2）mr_compare()
函数原型：int mr_compare(x,y)
参数类型：big x; big y
函数功能：比较两个大数的大小
返回值：x>y时返回+1, x=y时返回0, x （3）multiply()
函数原型：void multiply(x,y,z)
参数类型：big x,y,z
功能：计算两个大数的乘积，即z=x*y。
（4）xgcd()
函数原型：int xgcd(x,y,xd,yd,z)
参数类型： big x,y,xd,yd,z;
功能： 计算两个大数的扩展最大公约数，也可以用来计算模逆，这个函数比mad函数运算速度稍慢。z=gcd(x,y)=x.xd+y.yd，在此算法实现中，我选择此函数来进行模逆运算。
（5）add()
函数原型：void add(x,y,z)
参数类型：big x,y,z
功能：计算两个大数的和，即z=x+y。
（6）powmod()
函数原型：void powmod(x,y,z,w)
参数类型：big x,y,z,w;
功能：用来进行模幂运算，用表达式表示为w=x^y mod z。
（7）bigdig（）
函数原型：void bigdig(n,b,x)
参数类型：int n,b； big x
功能：产生一个指定长度的进制的随机数，该函数使用内置的随机数发生器，初始化种子调用irand函数
（8）isprime（）
函数原型：BOOL isprime(x)
参数类型：big x;
功能：判断一个大数是否为素数，使用概率测试算法
返回值：x为素数返回TRUE，否则返回FALSE

3.3算法实现的代码

/*1  3,5）门限秘密共享  t=3,n=5
2    500位左右的大整数，作为秘密，验收时给，每个放到一个txt文件中
3    随机生成5个d值
4    中间数据显示在屏幕上，包括5个d值，N值，M值，以及最后恢复了的秘密值
5    最后恢复秘密k，利用compare()函数，验证是否跟给的秘密相同*/
#include
#include"miracl.h"
#include
#define t 3
#define n 5
big d[n], ki[n];
int  CTR;

int main()
{
	miracl *mip = mirsys(5000, 10); //初始化miracl系统
	mip->IOBASE = 10;
	FILE *fp;
	char fname[100];
	printf("please input the name of the file of key: ");
	scanf("%s", fname);
	//读入文件里的key
	
	
		if ((fp = fopen(fname, "r+") )== NULL)
		{
			printf("file name error");
			return 0;
		}
		
	
	big k, temp;
	k = mirvar(0);
	temp = mirvar(0);
	/*随机创建一个秘密，这个秘密有500位
	bigdig(500, 10, k);
	printf("随机的秘密为:\n");
	*/
	cinnum(k, fp);
	printf("The key from file is ");
	cotnum(k, stdout);
	int i, j,m;
	for ( i = 0; i < n; i++)
	{
		d[i] = mirvar(0);
		ki[i] = mirvar(0);
	}
	//寻找合适的d1-d5
	//由于N=di*dj*dk>k>M=dm*dn因此生成的d可以都为200位的素数
	irand(time(NULL));
	for (i = 0; i < n; i++)
	{

		bigdig(200,10, d[i]);
		while (!(isprime(d[i])))//如果随机生成的di不为素数
		{
			bigdig(200,10, d[i]);
		}
	/*	printf("d%d :", i);
		cotnum(d[i], stdout);*/
	}
	//将随机生成符合条件的d进行排序
	printf("\n");
	for ( i = 0; i < n-1; i++)
	{
		for ( j = 0; j <n-1-i ; j++)
		{
			if (mr_compare(d[j], d[j + 1])==1)//d[j]>d[j+1]
			{
				temp = d[j];
				d[j] = d[j + 1];
				d[j + 1] = temp;
			}
		}

	}
	//输出排过序的d[]
	for ( i = 0; i < n; i++)
	{
		printf("d%d: ",i);
		cotnum(d[i], stdout);
		printf("\n");
	}
	big N, M, one;
	//计算N并输出
	N = mirvar(1);
	for ( i = 0; i < t; i++)
	{
		multiply(d[i], N, N);
	}
	printf("N = ");
	cotnum(N, stdout);

	//计算M并输出
	M = mirvar(1);
	one = mirvar(1);
	for ( i =n-t+2 ; i < n; i++)
	{
		multiply(d[i], M, M);
	}
	printf("M = ");
	cotnum(M, stdout);

	//根据密钥k和d[]计算ki[]
	for ( i = 0; i < n; i++)
	{
		powmod(k, one, d[i], ki[i]);//ki[i]=k mod di
	}
	/*for (i = 0; i < n; i++)
	{
		printf("k%d: ", i);
		cotnum(ki[i], stdout);
		printf("\n");
	}
	*/
	/******************密钥分割完毕******************/

	//密钥恢复
	big x;
	CRT( k);
	return 0;
}

int CRT(big k)
{
	miracl *mip = mirsys(5000, 10); //初始化miracl系统,注意进制
	mip->IOBASE = 10;
	big a1, a2, a3, m1, m2, m3, e1, e2, e3, one, Ma, Mb, Mc, Ma1, Mb1, Mc1, fu, x, m;
	a1 = mirvar(0);//初始化参数
	a2 = mirvar(0);
	a3 = mirvar(0);
	m1 = mirvar(0);
	m2 = mirvar(0);
	m3 = mirvar(0);
	e1 = mirvar(0);
	e2 = mirvar(0);
	e3 = mirvar(0);
	one = mirvar(1);
	fu = mirvar(-1);
	x = mirvar(0);
	m = mirvar(0);
	Ma = mirvar(0);
	Mb = mirvar(0);
	Mc = mirvar(0);
	Ma1 = mirvar(0);
	Mb1 = mirvar(0);
	Mc1 = mirvar(0);

	int num[t];
	printf("\n请选择三个子密钥 输入序列为0-4：");
	for (int i = 0; i < t; i++)
	{
		scanf("%d", &num[i]);
	}
	a1 = ki[num[0]];
	a2 = ki[num[1]];
	a3 = ki[num[2]];
	m1 = d[num[0]];
	m2 = d[num[1]];
	m3 = d[num[2]];
	//数字读取完毕,输出到屏幕上
	printf("a1 = ");
	cotnum(a1, stdout);
	printf("a2 = ");
	cotnum(a2, stdout);
	printf("a3 = ");
	cotnum(a3, stdout);
	printf("m1 = ");
	cotnum(m1, stdout);
	printf("m2 = ");
	cotnum(m2, stdout);
	printf("m3 = ");
	cotnum(m3, stdout);
	//判断mi是否互素
	egcd(m1, m2, e1);//e1=gcd(m1,m2)
	egcd(m1, m3, e2);
	egcd(m2, m3, e3);
	if (mr_compare(e1, one) == 0 && mr_compare(e2, one) == 0 && mr_compare(e3, one) == 0)
	{
		//计算M1 M2 M3
		multiply(m2, m3, Ma);//Ma=m2*m3
		multiply(m1, m3, Mb);
		multiply(m1, m2, Mc);

		//计算M1^-1  M2^-1 M3^-1
		xgcd(Ma, m1, Ma1, Ma1, Ma1);
		xgcd(Mb, m2, Mb1, Mb1, Mb1);
		xgcd(Mc, m3, Mc1, Mc1, Mc1);

		//计算X=M1M1^-1a1+M2M2^-1a2+M3^-1a3
		multiply(Ma, Ma1, e1);//e1=Ma*Ma^-1
		multiply(e1, a1, e1);//e1=Ma*Ma^-1*a1

		multiply(Mb, Mb1, e2);//e1=Mb*Mb^-1
		multiply(e2, a2, e2);//e1=Mb*Mb^-1*a2

		multiply(Mc, Mc1, e3);//e1=Mc*Mc^-1
		multiply(e3, a3, e3);//e1=Mc*Mc^-1*a3

		add(e1, e2, x);//x=e1+e2
		add(x, e3, x);//x=e1+e2+e3

		multiply(m1, m2, m);
		multiply(m, m3, m);//m=m1*m2*m3
		powmod(x, one, m, x);//x = x的一次方 mod m

		printf("\n恢复的密钥为 ： ");
		cotnum(x, stdout);
		//printf("\nmod ");
		//cotnum(m, stdout);
		if (mr_compare(k, x) == 0)
		{
			printf("\n密钥恢复正确！！");
		}
	}
	else
	{
		printf("\n(由于mi不互素)不能直接利用中国剩余定理！");
	}
	mirexit();// 清除MIRACL系统,释放所有内部变量
	return 0;
}

数据分析

通过测试老师验收时所给的多组数据，来验证编写算法代码的正确性
当秘密为secret0.txt时

当秘密为secret7.txt时

通过多组实验数据验证，可以确定程序的正确性没有问题，能够将秘密成功划分为多个子秘密，并且在t个子秘密下可以恢复秘密，而在t-1个子秘密下无法恢复。