2.Spatial Transformer Layer(李宏毅)
1.1简介
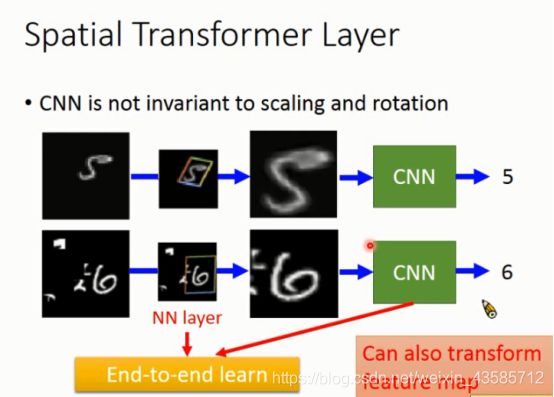
CNN并不存在几个特性:
1.Scaling的特性,filter size尺寸固定的情况下,大只狗与小只狗的形状并没有办法自动缩放辨识。
2.Rotation的特性,『3』转过来看起来对机器而言就是『m』。
3.也许仅有些许的Translation,但移动过多情况下对CNN来说也是不一样的。
上图范例,也许照片上有着缩小的『5』、『6』,但对机器而言两个数字应该就是很大,即使是单纯的缩放,对CNN而言也是不一样的东西。
因此Spatial Transformer Layer想做的事就是将图片做旋转缩放,让特征可以符合机器识别。
Spatial Transformer Layer本身也是一个NN layer,可以跟CNN并在一起直接训练,不仅可以Transform输入,所有的feature map都可以。
1.2 核心理论
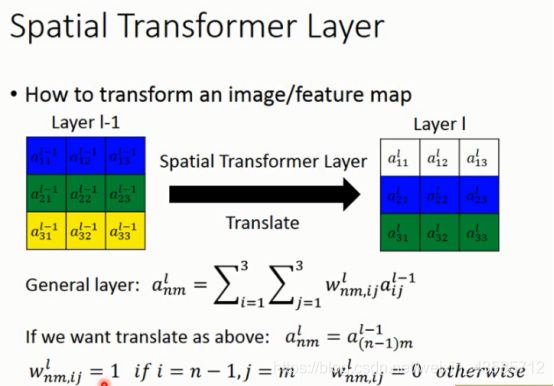
上图左是transform之前的照片 L a y e r l − 1 Layer^{l-1} Layerl−1,上图右是transform之后的照片 L a y e r l Layer^{l} Layerl,明显的发现到这个transform是将照片做了平移。
一般fully connect layer来说可以将Output视为Input与Weight的计算加总而得,它也可以做的到Transformation,只要对Weight做一些适当的调整。
上图为例,只要让 a n m l = a ( n − 1 ) m l − 1 a_{nm}^{l}=a_{(n-1)m}^{l-1} anml=a(n−1)ml−1,就是让这一层 n n n的值等于上一层的上一 n n n的值。
Weight设计成索引于 m n mn mn米且 i = n − 1 , = m i = n − 1 , = m i=n−1,=m的时候,那Weight=1,其余为0,这样就可以达成平移的目的。换句话说,如果要对照片做缩放或旋转的话,只需要对Weight做不同的设计就可以。
![]()
只需要对Weight做调整就可以达成平移(左)与旋转(右)的效果,要做到这种调整可以利用NN来控制。
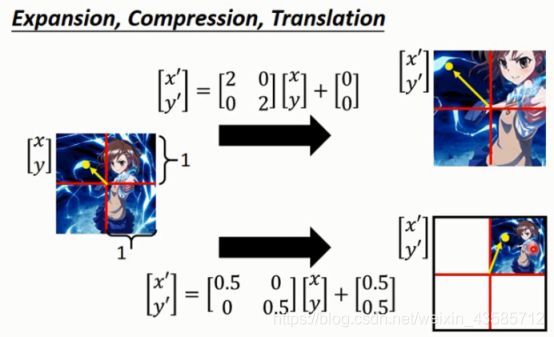
1.3Image Transformation
图上范例为放大两倍,因此乘上参数2,不做平移,因此最后加0。
图下范例为缩小两倍并且移至右上,因此乘上参数0.5最后加上平移值0.5。
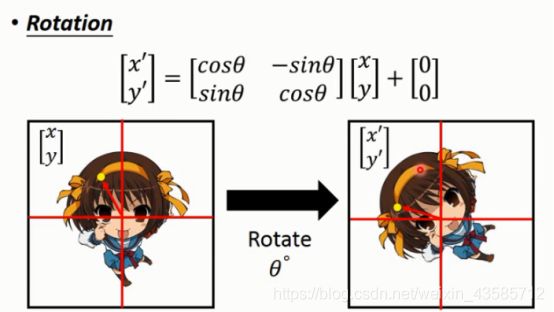
如果要将凉宫春日旋转,可以利用Sin, Cos来做调整。
1.4Spatial Transformer Layer
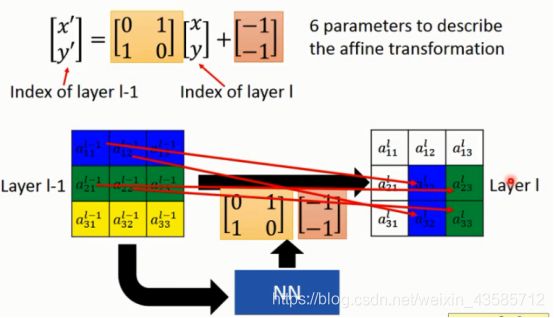
( x , y ) , ( x ′ , y ′ ) (x,y),(x^{'},y^{'}) (x,y),(x′,y′)是图像的索引,当 ( x ′ , y ′ ) (x^{'},y^{'}) (x′,y′)=(2,3),带入上面公式,可
( x , y ) (x,y) (x,y)=(1,2),其他的变换类似,结果如上图的箭头。
![]()
刚才说的是很刚好的得到的解都是整数,但如果不是的话就会有上图的结果, a 22 l a_{22}^{l} a22l接到小数点的索引,但这种索引是不存在的,因此我们可以将计算所得的索引取四舍五入 ( 1.6 , 2.4 ) ≈ ( 2 , 2 ) (1.6,2.4)\approx(2,2) (1.6,2.4)≈(2,2),得到 a 22 l − 1 a_{22}^{l-1} a22l−1,怪怪的对吧,不能这么做。
注意到,这种情况下是无法利用梯度下降来求解的,梯度是一种将参数做小小的变化,它对Output会有多少影响,对Spatial Transformer Layer的NN参数做小小的改变,也许 x ′ , y ′ x^{'},y^{'} x′,y′变为1.61,2.39,但四舍五入之后它接到的位置还是一样,代表Output没有任何变化,因此微分是『0』
1.41解决上面出现微分为0的方法
方案:插值
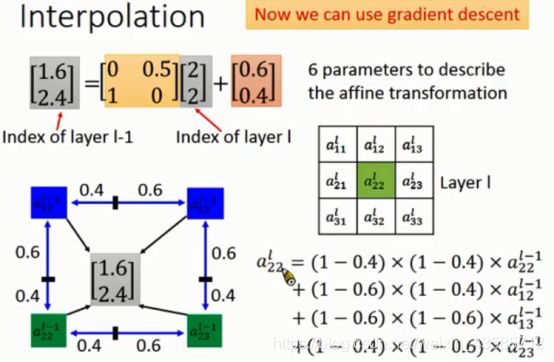
要处理小数点问题,就需要利用Interpolation,求出来的数值是有小数的,而这个小数索引实际上是在四个点 a ( 12 ) l − 1 , a ( 13 ) l − 1 , a ( 22 ) l − 1 , a ( 23 ) l − 1 a_{(12)}^{l-1},a_{(13)}^{l-1},a_{(22)}^{l-1},a_{(23)}^{l-1} a(12)l−1,a(13)l−1,a(22)l−1,a(23)l−1的区间内,我们不单纯的参考它跟距离最近的那个点 a ( 22 ) l − 1 a_{(22)}^{l-1} a(22)l−1,而是四个点的数值都参考。
这种情况下NN参数有些微的变化的时候Output也会有些微的变化,就可以利用梯度下降来优化求解了。
1.5 完整STN网络结构
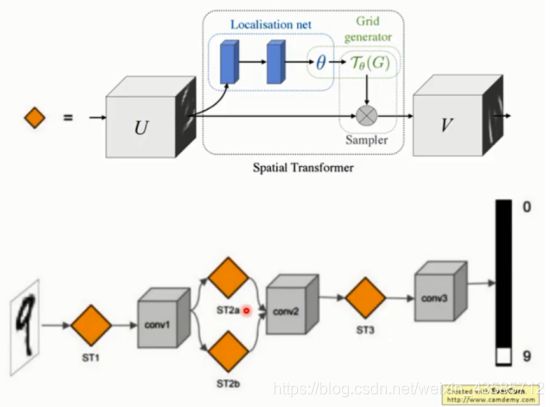
这个网络可以加入到CNN的任意位置,而且相应的计算量也很少。
将 spatial transformers 模块集成到 cnn 网络中,允许网络自动地学习如何进行 featuremap 的转变,从而有助于降低网络训练中整体的代价。定位网络中输出的值,指明了如何对每个训练数据进行转化。
2. 应用
1.翻译杂乱的MNIST: 应用于MINIS上,不论数值如何的平移、旋转,对Output都没有影响。
2.街景门牌号
3.鸟类的辨识案例
参考链接