清风数学建模学习笔记——逻辑回归的二分类模型

二分类模型

  对于二分类模型，本文将介绍逻辑回归 (logistic regression) 的分类算法。后文还将介绍应用 SPSS 进行回归的案例分析。

---

---

一、逻辑回归 logistic regression 介绍

  对于因变量为分类变量的情况，我们可以使用逻辑回归进行处理。把 $y$ 看成事件发生的概率，$y$ > 0.5 表示发生；$y$ < 0.5 表示不发生。

  如：是否违约、是否得病…

---

二、模型推导

线性概率模型 LPM：

  针对以上的思路可以用线性概率回归模型进行回归。

$$\begin{gathered} y_i={\beta }_0+{\beta }_1{x}_{1i}+{\beta }_2{x}_{2i}+\cdots +{\beta }_k{x}_{ki}+{\mu }_i \\ 写成向量乘积形式：y_i=x_i^{{}^{\prime }}\beta +u_i(i=1,2,...,n) \end{gathered}$$

线性概率模型存在一定的问题：

问题1：
  应用线性概率模型必然会讨论扰动项 ui 与其他自变量是否存相关，如果存在那么就会产生 内生性问题，即回归系数估计出来不一致且有偏。
  因为二分类估计出来的 $y_i$ 只能是 0 或者 1。因此扰动项可以转换成以下形式：
$$u_i=\{\begin{array}{l}1-x_i^{{}^{\prime }}\beta ,y_i=1\\ -x_i^{{}^{\prime }}\beta ,y_i=0\end{array}$$

  那么很显然 $u_i$ 与 自变量 $x_i$ 必然会存在关系，即相关系数或协方差不为零，$cov(x_i,u_i)\ne 0$。因此模型存在内生性问题。

问题2：
$${\hat{y}}_i={\hat{\beta }}_0+{\hat{\beta }}_1{x}_{1i}+{\hat{\beta }}_2{x}_{2i}+\cdots +{\hat{\beta }}_k{x}_{ki}$$

  预测值可能会出现 $y_i$>1 或者 $y_i$<0，因为 yi 代表的是概率，因此这种预测值不现实。

---

两点分布对于线性模型的修正：

事件	1	0
概率	p	1-p

  在给定 $x$ 的情况下，考虑 $y$ 的两点分布概率。
$$\begin{gathered} \{\begin{array}{l}P(y=1|x)=F(x,\beta )\\ P(y=0|x)=1-F(x,\beta )\end{array}注：一般F(x,\beta )=F(x_i^{{}^{\prime }}\beta ) \\ F(x,\beta )实际上取：y_i={\beta }_0+{\beta }_1{x}_{1i}+{\beta }_2{x}_{2i}+\cdots +{\beta }_k{x}_{ki}+{\mu }_i \end{gathered}$$

  $F(x,\beta )$ 成为连接函数，它将解释变量 $x$ 与被解释变量 $y$ 连接起来。那么需要保证 $F(x,\beta )$ 是定义在区间 [0, 1] 之间，即可保证: 0 ≤ $\hat{y}$ ≤ 1。

  此外，上文的定义是值域，理解为 $F(x,\beta )$ 的值域 [0, 1]，因为对 $y$ 求期望等于 $y$ 的概率：$E(y|x)=1\times P(y=1|x)+0\times P(y=0|x)=P(y=1|x)$，因此我们可以将 $y$ 的预测值 $\hat{y}$ 理解为 $y=1$ 发生的概率。

---

连接函数的取法：

取法1：取标准正态分布的累计密度函数(cdf)   $⟹$  probit回归

$$F(x,\beta )=\Phi (x_i^{{}^{\prime }}\beta )={\int }_{-\infty }^{x_i^{{}^{\prime }}\beta }\frac{1}{\sqrt{2\pi }}{e}^{-\frac{t^2}{2}}dt$$

取法2：取 Sigmoid 函数  $⟹$ logistic回归

$$F(x,\beta )=S(x_i^{{}^{\prime }}\beta )=\frac{exp(x_i^{{}^{\prime }}\beta )}{1+exp(x_i^{{}^{\prime }}\beta )}$$

  由于后者有解析表达式（而标准正态分布的cdf没有），所以计算 logistic 模型比 probit 模型更为方便。

---

求解：

  因为 Sigmoid 是一个非线性的模型，因此使用极大似然估计（MLE） 进行估计。

$$\{\begin{array}{l}P(y=1|x)=S(x_i^{{}^{\prime }}\beta )\\ P(y=0|x)=1-S(x_i^{{}^{\prime }}\beta )\end{array}\Rightarrow f(y_i|x_i,\beta )=\{\begin{array}{l}P(y=1|x)=S(x_i^{{}^{\prime }}\beta ),y_i=1\\ P(y=0|x)=1-S(x_i^{{}^{\prime }}\beta ),y_i=0\end{array}$$

  写成更加紧凑的形式：

$$\begin{gathered} f(y_i|x_i,\beta )=[S(x_i^{{}^{\prime }}\beta ){]}^{y_i}[1-S(x_i^{{}^{\prime }}\beta ){]}^{1-y_i} \\ 取对数：\ln (y_i|x_i,\beta )=y_i\ln [S(x_i^{{}^{\prime }}\beta )]+(1-y_i)\ln [1-S(x_i^{{}^{\prime }}\beta )] \\ 样本得对数似然函数：\ln L(\beta |y,x)=\sum _{i=1}^n{y}_i\ln [S(x_i^{{}^{\prime }}\beta )]+\sum _{i=1}^n(1-y_i)\ln [1-S(x_i^{{}^{\prime }}\beta )] \end{gathered}$$

  最终可以使用数值方法（梯度下降）求解这个非线性最大化的问题。
$${\hat{y}}_i=P(y_i=1|x)=S(x_i^{{}^{\prime }}\hat{\beta })=\frac{exp(x_i^{{}^{\prime }}\hat{\beta })}{1+exp(x_i^{{}^{\prime }}\hat{\beta })}=\frac{e^{{\hat{\beta }}_0+{\hat{\beta }}_1{x}_{1i}+{\hat{\beta }}_2{x}_{2i}+\cdots +{\hat{\beta }}_k{x}_{ki}}}{1+e^{{\hat{\beta }}_0+{\hat{\beta }}_1{x}_{1i}+{\hat{\beta }}_2{x}_{2i}+\cdots +{\hat{\beta }}_k{x}_{ki}}}$$

  如果 $y$ ≥0.5，则认为其预测的 $y$ =1;否则则认为其预测的 $y$ =0

---

三、应用 Spss 求解逻辑回归

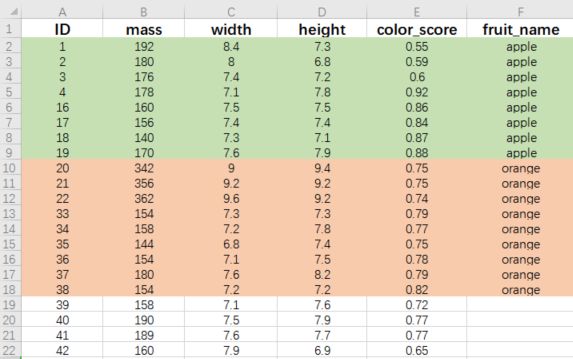
例：题目中给出了部分水果的相应属性与结果，根据已知水果的属性特征对未知水果进行分类。（题目截取了部分数据，实际数据苹果橙子各19条）

• mass: 水果重量
• width: 水果的宽度
• height: 水果的高度
• color_score: 水果的颜色数值，范围0‐1
• fruit_name：水果类别
  

---

数据预处理：定性变量转换成定量变量

  定性变量就是取值不是数值，是指定字符串的。如：生病、未生病。那么对数据进行分析就要将定性变量转换成定量变量。转换的方法就是生成虚拟变量，这个虚拟值就代表着样本属性的一种状态。如：生病为1，未生病为0。

生成虚拟变量的方式有如下两种：

第一种：Spss生成虚拟变量
    
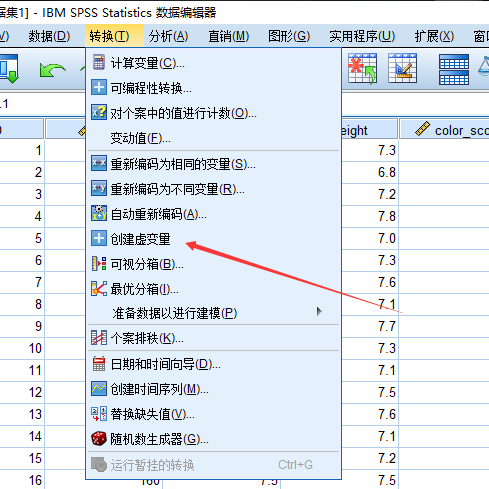
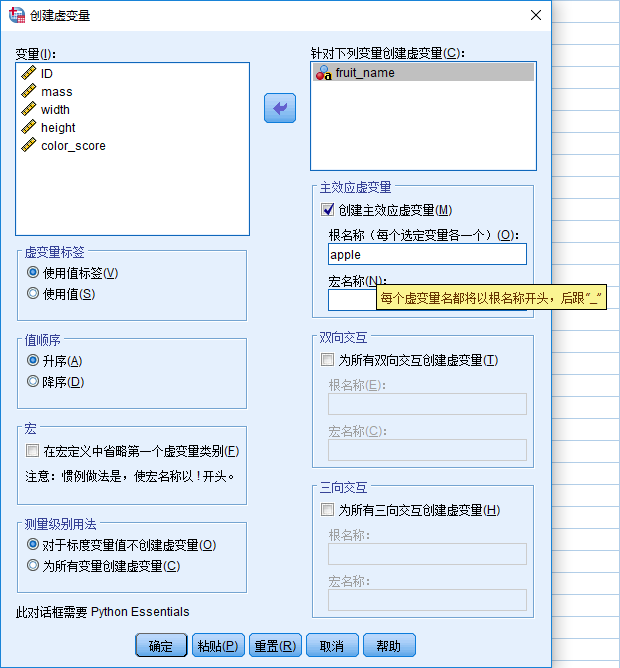
  当然这会根据定性变量属性值的数量生成对应的列数，如：本题判断水果是苹果还是橙子，那么设置虚拟变量苹果为 1，橙子为 0，反过来也可以，因此 Spss 会生成两列数据，只需留一列就可以。

  若 Spss 中没有可以去扩展中心扩展，如果扩展不了可以用第二种方法进行手动生成虚拟变量。

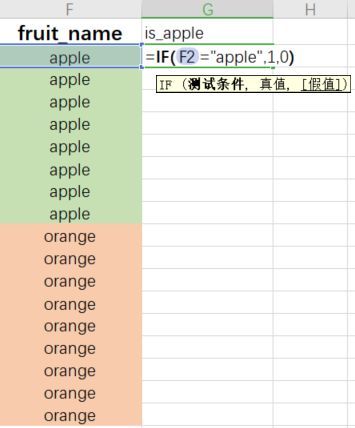
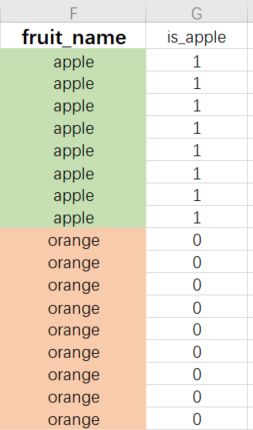
第二种：Excel生成虚拟变量

  最终生成的结果如右图:
      

---

求解逻辑回归：

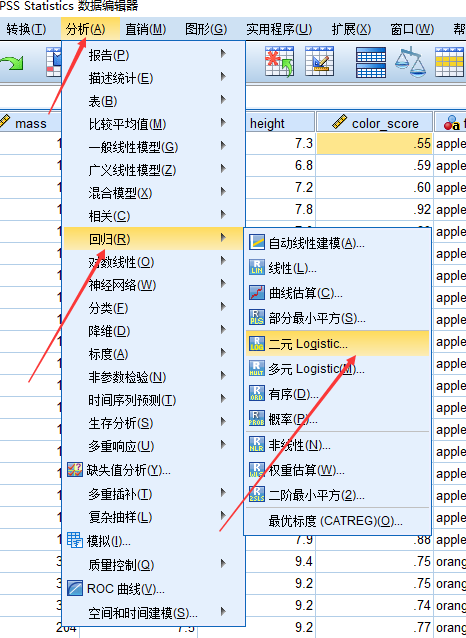
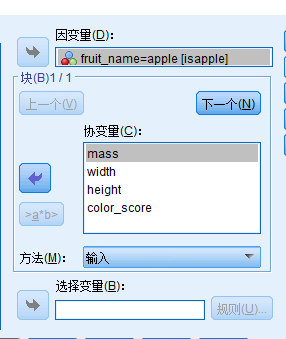
分析 => 回归 => 二元Logistic => 选择因变量与自变量（这里如果是定性变量，那么就需要选择对应的虚拟变量）=> 选择保存，并勾选概率与组成员
     

---

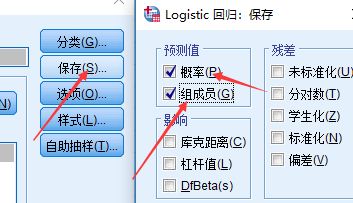
结果分析：

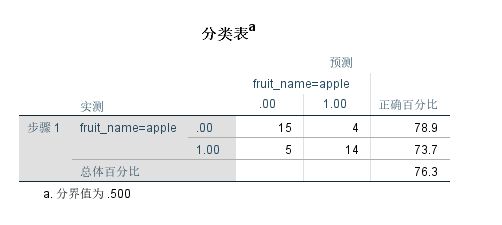
• 19个苹果样本中，预测出来为苹果的有14个，预测出来的正确率为73.7%;
• 19个橙子样本中，预测出来为橙子的有15个，预测出来的正确率为78.9%;
• 对于整个样本，逻辑回归的预测成功率为76.3%.
  
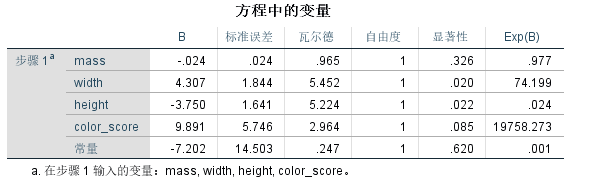
• B 代表着估计出来的相关系数，显著性实际对应着 P 值。
• 在 95% 的置信水平下，P值小于0.05的属性，就代表着该属性显著。
• 对显著性水平进行解释：对一个回归结果的好坏需要进行假设检验。设置联合显著性检验 $H_0：{\beta }_1={\beta }_2=...={\beta }_k=0$，检验 $k$ 个自变量的系数是否为 0。假如没有拒绝 $H_0$，即 P 值求出值＞0.05，就是说无法拒绝$H_0$（95%的置信水平下这种假设存在概率超过5%），因此最终下结论，这个联合性检验无法拒绝原假设，此时回归无任何意义。当然这是评判整体回归的结果的标准，也可以设置90%的置信水平。如果要查看单个自变量的显著程度只需要查看显著性小于0.05即可（95%置信水平）。
• 从表中可以看出 width、height 在95%的置信水平下显著。如果是90%的置信水平显著变量还要添加 color_score。
  
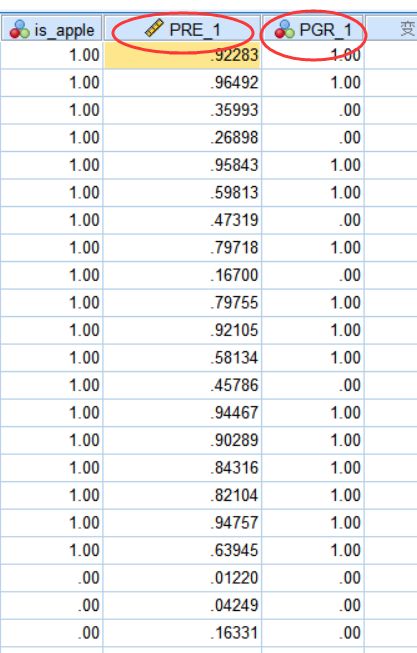
• 第一列代表的是 $\hat{y}$ 即预测值，说明有多大的概率为苹果。
• 第二列代表的是回归的结果，1代表是苹果，0代表是橙子。当然这里 y^ 对应的概率分别是大于0.5，小于0.5。
  

  ---

  
  扩展：
    如果回归结果不是很满意，那么可以加入自变量的平方或者加入交互项等
       
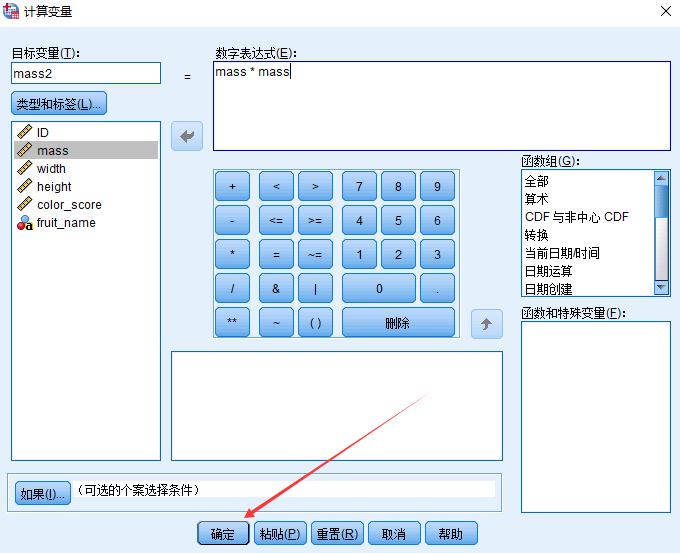
    结果会比原来好很多，甚至会出现100%的正确比，但是会出现 过拟合 的现象，对于样本数据的预测非常好，但是对于样本外的数据的预测效果可能会很差。

  对于以上情况，可以使用 交叉验证 的方法进行反复多次，最终取平均准确率。把数据分为训练组和测试组，比例为80%和20%。那么已知分类结果的水果ID为1‐38，前19个为苹果，后19个为橙子。每类水果中随机抽出3个ID作为测试组，剩下的16个ID作为训练组。（比如：17‐19、36‐38这六个样本作为测试组）比较设置不同的自变量后的模型对于测试组的预测效果。

---

  本文借鉴了数学建模清风老师的课件与思路，如果大家发现文章中有不正确的地方，欢迎大家在评论区留言，也可以点击查看下方链接查看清风老师的视频讲解~

原文链接：https://www.bilibili.com/video/BV1DW411s7wi