matlab——非线性规划
matlab——非线性规划
- 非线性规划的定义
- 非线性规划的Matlab解法
- 无约束问题的Matlab解法
-
- 无约束问题的符号解
- 无约束极值问题的数值解
- 约束极值问题
-
- 二次规划
- 罚函数法
- Matlab求约束极值问题
非线性规划的定义
如果目标函数或约束条件中包含非线性函数,就称这种规划问题为非线性规划问题。
非线性规划目前还没有适于各种问题的一般算法,各个方法都有自己特定的适用范围。
除了常数项每项的次数都是一次的就是线性函数,如果出现平方和开方就是非线性函数。
非线性规划的Matlab解法
Matlab中非线性规划的数学模型写成以下形式:
m i n f ( x ) , s . t . { A ⋅ x ≤ b , A e q ⋅ x = b e q , c ( x ) ≤ 0 , c e q ( x ) = 0 , l b ≤ x ≤ u b 。 \qquad\qquad\qquad\qquad\qquad minf(x),\\ \qquad\qquad\qquad\qquad s.t.\begin{cases}A\cdot x\leq b,\\ Aeq\cdot x=beq,\\ c(x)\leq 0,\\ ceq(x)=0,\\ lb\leq x\leq ub。\end{cases} minf(x),s.t.⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧A⋅x≤b,Aeq⋅x=beq,c(x)≤0,ceq(x)=0,lb≤x≤ub。
式中: c ( x ) , c e q ( x ) c(x),ceq(x) c(x),ceq(x)为非线性向量函数。
Matlab中的命令是
[ x , f v a l ] = f m i n c o n ( f u n , x 0 , A , b , A e q , b e q , l b , u b , n o n l c o n , o p t i o n s ) [x,fval]=fmincon(fun,x_0,A,b,Aeq,beq,lb,ub,nonlcon,options) [x,fval]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
如果没有线性约束,则填入"[ ]"就行。
f u n fun fun是用M文件定义的函数 f ( x ) ; f(x); f(x); n o n l c o n nonlcon nonlcon是用M文件定义的非线性向量函数 c ( x ) , c e q ( x ) ; o p t i o n s c(x),ceq(x);options c(x),ceq(x);options定义了优化参数,可以使用Matlab默认的参数设置。
例 求下列非线性规划:
m i n f ( x ) = x 1 2 + x 2 2 + x 3 2 + 8 , s . t . { x 1 2 − x 2 + x 3 2 ≥ 0 , x 1 + x 2 2 + x 3 3 ≤ 20 , − x 1 − x 2 2 + 2 = 0 , x 2 + 2 x 3 2 = 3 , x 1 , x 2 , x 3 ≥ 0 。 \qquad\qquad\qquad\qquad\qquad minf(x)=x_1^2+x_2^2+x_3^2+8,\\ \qquad\qquad\qquad\qquad\qquad \\ \qquad\qquad\qquad\qquad\qquad s.t.\begin{cases} x_1^2-x_2+x_3^2\geq0,\\ x_1+x_2^2+x_3^3\leq20,\\ -x_1-x_2^2+2=0,\\ x_2+2x_3^2=3,\\ x_1,x_2,x_3\geq0。\end{cases} minf(x)=x12+x22+x32+8,s.t.⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧x12−x2+x32≥0,x1+x22+x33≤20,−x1−x22+2=0,x2+2x32=3,x1,x2,x3≥0。
解 (1)编写M函数fun1.m定义目标函数:
function f=fun1(x);
f=sum(x.^2)+8;%x是向量,里面已经包含了x1,x2,x3,矩阵用.^是将各元素平方。
(2)编写M函数fun2.m定义非线性约束条件:
function [g,h]=fun2(x);
g=[-x(1)^2+x(2)-x(3)^2
x(1)+x(2)^2+x(3)^3-20];%非线性不等式约束 这里第一个式子变号了,因为Matlab标准型要用≤的不等式
h=[-x(1)-x(2)^2+2
x(2)+2*x(3)^2-3];%非线性等式约束
(3)编写主程序文件如下:
[x,y]=fmincon('fun1',rand(3,1),[],[],[],[],zeros(3,1),[],'fun2')
求得当 x 1 x_1 x1=0.5522, x 2 x_2 x2=1.2033, x 3 x_3 x3=0.9478时,最小值 y y y=10.6511。
(rand函数的问题后面一起说)
无约束问题的Matlab解法
无约束问题的符号解
例 求多元函数 f ( x , y ) = x 3 − y 3 + 3 x 2 + 3 y 2 − 9 x f(x,y)=x^3-y^3+3x^2+3y^2-9x f(x,y)=x3−y3+3x2+3y2−9x的极值。
解 先解方程组
{ f x ( x , y ) = 3 x 2 + 6 x − 9 = 0 , f y ( x , y ) = − 3 y 2 + 6 y = 0 。 \qquad\qquad\qquad\qquad\qquad\begin{cases} f_x(x,y)=3x^2+6x-9=0,\\ f_y(x,y)=-3y^2+6y=0。 \end{cases} {fx(x,y)=3x2+6x−9=0,fy(x,y)=−3y2+6y=0。
上式是对多元函数求偏导,求得驻点为 ( 1 , 0 ) , ( 1 , 2 ) , ( − 3 , 0 ) , ( − 3 , 2 ) 。 (1,0),(1,2),(-3,0),(-3,2)。 (1,0),(1,2),(−3,0),(−3,2)。
再求出Hessian阵
[ ∂ 2 f ∂ x 2 ∂ 2 f ∂ x ∂ y ∂ 2 f ∂ x ∂ y ∂ 2 f ∂ y 2 ] = [ 6 + 6 x 0 0 6 − 6 y ] , \qquad\qquad\qquad\qquad\qquad\begin{bmatrix} \dfrac{\partial ^2f}{\partial x^2}& \dfrac{\partial ^2f}{\partial x\partial y}\\\\ \dfrac{\partial ^2f}{\partial x\partial y}& \dfrac{\partial ^2f}{\partial y^2}\end{bmatrix} = \begin{bmatrix}6+6x&0 \\ 0&6-6y\end{bmatrix}, ⎣⎢⎢⎢⎢⎡∂x2∂2f∂x∂y∂2f∂x∂y∂2f∂y2∂2f⎦⎥⎥⎥⎥⎤=[6+6x006−6y],
如果在驻点处Hessian阵为正定阵,则在该点取极小值;如果在驻点处Hessian阵为负定阵,则在该点取极大值;如果在驻点处Hessian阵为不定阵,则该驻点不是极值点。
(我先解释Hessian阵)
其实Hessian阵就是求二阶偏导数,比如 f ( x , y ) f(x,y) f(x,y)求一阶偏导得出 ∂ f ∂ x \dfrac{\partial f}{\partial x} ∂x∂f和 ∂ f ∂ y \dfrac{\partial f}{\partial y} ∂y∂f。而Hessian阵中第一行就是在 ∂ f ∂ x \dfrac{\partial f}{\partial x} ∂x∂f的基础上再对每一个变量求二阶偏导,第二行就是在 ∂ f ∂ y \dfrac{\partial f}{\partial y} ∂y∂f的基础上再对每个变量求二阶偏导,3个变量的多元函数以此类推。
(下面解释正定阵、负定阵以及不定阵)
求出矩阵的所有特征值,如果特征值全是正的则为正定阵,都是负的则为负定阵。
不定阵则需要引入半正定阵和半负定阵的概念。半正定阵指的是特征值是≥0,半负定阵则是特征值≤0,即在正定阵和负定阵中多一个等于0的条件,若一个矩阵既不是半正定阵也不是半负定阵,则该矩阵为不定阵。可以使用Matlab中的eig函数直接求特征值即可。
补充一个概念,当矩阵为半正定阵或半负定阵时为可疑极值点,需要别的方法判定。
上面可以得出点 ( 1 , 0 ) (1,0) (1,0)是极小值点, ( − 3 , 2 ) (-3,2) (−3,2)是极大值点。
计算的Matlab程序如下:
clc,clear
syms x y;
f=x^3-y^3+3*x^2+3*y^2-9*x;
df=jacobian(f); %求一阶偏导数(可以自动判断变量的个数)
d2f=jacobian(df); %求Hessian阵
[xx,yy]=solve(df); %求驻点
xx=double(xx);yy=double(yy);%转化成double型数据,下面判断特征值的正负必须是数值型数据
for i=1:length(xx)
a=subs(d2f,{x,y},{xx(i),yy(i)});%这个函数下面说,功能是以xx替代x,即将驻点带进Hessian矩阵中
b=eig(a); %求矩阵的特征值
f=subs(f,{x,y},{xx(i),yy(i)});f=double(f);
if all(b>0)
fprintf('(%f,%f)是极小值点,对应的极小值为%f\n',xx(i),yy(i),f);
elseif all(b<0)
fprintf('(%f,%f)是极大值点,对应的极大值为%f\n',xx(i),yy(i),f);
elseif any(b>0)&any(b<0)
fprintf('(%f,%f)不是极值点\n',xx(i),yy(i));
else
fprintf('无法判断(%f,%f)是否是极值点\n',xx(i),yy(i));
end
end
因为这里是符号函数,所以出现的都是x,y,使用subs函数以新值代替符号变量。
subs(s,old,new)返回s,替换所有发生在old带着new,然后评估s.
subs(s,new)返回s中替换默认变量的所有出现。s带着new,然后评估s。默认变量由symvar.
subs(s)返回s中的符号变量替换s,并从调用函数和matlab中得到它们的值。然后计算s。没有赋值的变量仍然作为变量。
syms a b
subs(a + b, a, 4)
ans =b + 4
(将a+b中的a替换成4,因为b还是符号变量所以ans是b+4,如果b不是符号变量,会直接计算出结果)
B = all(A)
- 沿着大小不等于 1 的数组 A 的第一维测试所有元素为非零还是逻辑值 1 (true)。
- 如果 A 为向量,当A的所有元素为非零时,all(A)返回逻辑 1 (true),当一个或多个元素为零时,返回逻辑 0 (false)。
- 如果 A 为非空非向量矩阵,all(A) 将 A的各列视为向量,返回包含逻辑 1 和 0 的行向量。
通常会搭配if使用,即if语句先进行对条件的判断得出0或1,再使用all判断是否都满足条件。
B = any(A)
- 沿着大小不等于 1 的数组 A 的第一维测试所有元素为非零数字还是逻辑值 1 (true)。
- 如果 A 为向量,当 A 的任何元素是非零数字或逻辑 1 (true) 时,B = any(A) 返回逻辑 1,当所有元素都为零时,返回逻辑 0 (false) 。
- 如果 A 为非空非向量矩阵,B = any(A) 将 A 的各列视为向量,返回包含逻辑 1 和 0 的行向量
使用方法同all差不多。
无约束极值问题的数值解
在Matlab工具箱中,用于求解无约束极小值问题的函数有 f m i n u n c fminunc fminunc和 f m i n s e a r c h fminsearch fminsearch ,用法介绍如下:
Matlab中 f m i n u n c fminunc fminunc的基本命令是
[ x , f v a l ] = f m i n u n c ( f u n , x 0 , o p t i o n s ) [x,fval]=fminunc(fun,x0,options) [x,fval]=fminunc(fun,x0,options)
其中:返回值 x x x是所求得的极小值点,返回值 f v a l fval fval是函数的极小值。 f u n fun fun是一个M函数,当fun只有一个返回值时,它的返回值时函数 f ( x ) f(x) f(x);当 f u n fun fun有两个返回值时,它的第二个返回值是 f ( x ) f(x) f(x)的梯度向量;当 f u n fun fun有三个返回值时,它的第三个返回值是 f ( x ) f(x) f(x)的二阶导数阵(Hessian阵)。 x 0 x0 x0是 x x x的初始值, o p t i o n s options options是优化参数,可以使用默认参数。
这个的返回值就是定义M函数文件时的 f u n c t i o n [ v a r 1 , v a r 2 , v a r 3 ] = f u n ( x ) function\quad[var1,var2,var3]=fun(x) function[var1,var2,var3]=fun(x),一般来说,提供的信息越多,计算越快,精度越高。 x 0 x0 x0一般用 r a n d rand rand函数获取随机数,求解器使用 x 0 x0 x0 中的元素数量和 x 0 x0 x0的大小来确定 f u n fun fun接受的变量数量和大小。
梯度向量就是求一阶偏导数!!
求多元函数的极小值也可以使用Matlab的 f m i n s e a r c h fminsearch fminsearch命令 ( f m i n s e a r c h fminsearch fminsearch算法实现是无导数法,所以无法使用梯度)
[ x , f v a l ] = f m i n s e a r c h ( f u n , x 0 , o p t i o n s ) [x,fval]=fminsearch(fun,x0,options) [x,fval]=fminsearch(fun,x0,options)
例 求多元函数 f ( x , y ) = x 3 − y 3 + 3 x 2 + 3 y 2 − 9 x f(x,y)=x^3-y^3+3x^2+3y^2-9x f(x,y)=x3−y3+3x2+3y2−9x的极值。
解 编写Matlab程序如下:
clc,clear
f=@(x) x(1)^3-x(2)^3+3*x(1)^2+3*x(2)^2-9*x(1);
g=@(x)-f(x);
[xy1,z1]=fminunc(f,rand(2,1)) %求极小值点
[xy2,z2]=fminsearch(g,rand(2,1)); %求极大值点
xy2,z2=-z2 %第一条没有使用;会直接显示结果
求得的极小值点为 ( 1 , 0 ) (1,0) (1,0),极小值为-5;极大值点为 ( − 3 , 2 ) (-3,2) (−3,2),极大值为31。
注:fminsearch只能求给定的初始值附近的一个极小值点。
例 求函数 f ( x ) = 100 ( x 2 − x 1 2 ) 2 + ( 1 − x 1 ) 2 f(x)=100(x_2-x_1^2)^2+(1-x_1)^2 f(x)=100(x2−x12)2+(1−x1)2的极小值。
解 在求极小值时,可以使用函数的梯度,编写M函数fun3.m如下:
function [f,g]=fun3(x);
f=100*(x(2)-x(1)^2)^2+(1-x(1))^2;
g=[-400*x(1)*(x(2)-x(1)^2)-2*(1-x(1));200*(x(2)-x(1)^2)]; %g返回的是梯度向量
编写的主程序文件如下:
options=optimset('GradObj','on'); %我认为是利用梯度的意思
[x,y]=fminunc('fun3',rand(1,2),options)
求得函数的极小点 ( 1 , 1 ) (1,1) (1,1),函数的极小值为 3.9917 × 1 0 − 15 3.9917\times10^{-15} 3.9917×10−15,即极小值近似为0。
也可以利用二阶导数,这里就不再说了。
约束极值问题
二次规划
若某非线性规划的目标函数为自变量 x x x的二次函数,约束条件又全是线性的,就称这种规划为二次规划。
Matlab中求解二次规划的命令是
[ x , f v a l ] = q u a d p r o g ( H , f , A , b , A e q , b e q , l b , u b , x 0 , o p t i o n s ) [x,fval]=quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options) [x,fval]=quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)
H是实对称矩阵,这里要明白二次型函数怎么转化成二次型矩阵。
平方项 x i 2 x_i^2 xi2的系数放在主对角线第 i i i行第 i i i列的位置, x i x j x_ix_j xixj的系数除以2放在第 i i i行第 j j j列和第 j j j行第 i i i列的位置,如果没有则写0。
但是因为Matlab中二次规划的数学模型中目标函数如下:
m i n 1 2 x T H x + f T x \qquad\qquad\qquad\qquad\qquad\qquad min\quad\dfrac{1}{2}x^THx+f^Tx min21xTHx+fTx
所以H在使用中实际上要乘以2才能得出原本的二次函数。
例 求解二次规划
m i n f ( x ) = 2 x 1 2 − 4 x 1 x 2 + 4 x 2 2 − 6 x 1 − 3 x 2 , s . t . { x 1 + x 2 ≤ 3 , 4 x 1 + x 2 ≤ 9 , x 1 , x 2 ≥ 0 。 \qquad\qquad\qquad\qquad\qquad minf(x)=2x_1^2-4x_1x_2+4x_2^2-6x_1-3x_2,\\ \qquad\qquad\qquad\qquad\qquad s.t.\begin{cases}x_1+x_2\leq3,\\ 4x_1+x_2\leq9,\\ x_1,x_2\geq0。\end{cases} minf(x)=2x12−4x1x2+4x22−6x1−3x2,s.t.⎩⎪⎨⎪⎧x1+x2≤3,4x1+x2≤9,x1,x2≥0。
解 编写如下程序:
h=[4,-4;-4,8]; %在求出的实对称矩阵中乘以2
f=[-6;-3]; %这是剩下的一次项的系数
a=[1,1;4,1];
b=[3;9];
[x,fval]=quadprog(h,f,a,b,[],[],zeros(2,1))
求得 x 1 x_1 x1=1.9500, x 2 x_2 x2=1.0500, m i n f ( x ) minf(x) minf(x)=-11.0250。
罚函数法
利用罚函数法,可将非线性规划问题的求解,转化为求解一系列无约束极值问题,因而也称这种方法为序列无约束最小化技术。
- 罚函数法求解非线性规划问题的思想是,利用问题中的约束函数作出适当的罚函数,由此构造出带参数的增广目标函数,把问题转化为无约束非线性规划问题。主要有两种形式,一种叫外罚函数法,另一种叫内罚函数法,下面介绍外罚函数法。内罚函数只适用于不等式约束,而外罚函数适用于不等式约束以及等式约束。
例 求下列非线性规划
m i n f ( x ) = x 1 2 + x 2 2 + 8 , s . t . { x 1 2 − x 2 ≥ 0 , − x 1 − x 2 2 + 2 = 0 , x 1 , x 2 ≥ 0 。 \qquad\qquad\qquad\qquad\qquad minf(x)=x_1^2+x_2^2+8,\\ \qquad\qquad\qquad\qquad\qquad s.t.\begin{cases}x_1^2-x_2\geq0,\\ -x_1-x_2^2+2=0,\\ x_1,x_2\geq0。\end{cases} minf(x)=x12+x22+8,s.t.⎩⎪⎨⎪⎧x12−x2≥0,−x1−x22+2=0,x1,x2≥0。
解 (1)定义增广目标函数,编写M函数test1.m如下:
function g=test1(x);
M=50000;
f=x(1)^2+x(2)^2+8;
g=f-M*min(x(1),0)-M*min(x(2),0)-M*min(x(1)^2-x(2),0)+M*abs(-x(1)-x(2)^2+2);
如果 x 1 , x 2 < 0 x_1,x_2<0 x1,x2<0的话,式中是 − M ∗ m i n ( x 1 , 0 ) -M*min(x_1,0) −M∗min(x1,0),则相当于加上了一个充分大的数,因为是求极小值,加上一个充分大的数之后,就不会影响结果。其他条件也是这种思路。(abs是取绝对值,只要等式不成立,就会加上一个充分大的数。)
(2)求增广目标函数的极小值,在Matlab命令窗口中输入:
[x,y]=fminsearch('test3',rand(2,1))
即可求得问题的解。由于是非线性问题,很难求得问题的全局最优解,因此只能求得一个局部最优解并且每次的运行结果都是不一样的。(凸规划可以求得整体解)
如果非线性规划问题要求实时算法,则可以使用罚函数方法,但计算精度较低。(实时算法即当时得出数据。)
Matlab求约束极值问题
在Matlab优化的工具箱中,用于求解约束最优化问题的函数有 f m i n b n d 、 f m i n c o n 、 q u a d p r o g 、 f s e m i n f 、 f m i n i m a x fminbnd、fmincon、quadprog、fseminf、fminimax fminbnd、fmincon、quadprog、fseminf、fminimax,上面已经介绍了函数 f m i n c o n fmincon fmincon和 q u a d p r o g quadprog quadprog。
- f m i n b n d fminbnd fminbnd函数
求单变量非线性函数在区间上的极小值(就是没有别的约束条件,只有变量区间约束)
m i n x f ( x ) , x ∈ [ x 1 , x 2 ] \qquad\qquad\qquad\qquad\qquad min_xf(x),x\in[x_1,x_2] minxf(x),x∈[x1,x2]
Matlab的命令为
[ x , f v a l ] = f m i n b n d ( f u n , x 1 , x 2 , o p t i o n s ) [x,fval]=fminbnd(fun,x_1,x_2,options) [x,fval]=fminbnd(fun,x1,x2,options)
f u n fun fun是用M文件定义的函数、匿名函数 (即@(x)) 或Matlab中的但变量函数。
这里就不举例了。
f s e m i n f fseminf fseminf函数我没理解透,就不说了。
- f m i n i m a x fminimax fminimax函数
求解
m i n x m a x i F i ( x ) , \qquad\qquad\qquad\qquad\qquad min_x\quad max_iF_i(x), minxmaxiFi(x),
s . t . { A ⋅ x ≤ b , A e q ⋅ x = b e q , c ( x ) ≤ 0 , c e q ( x ) = 0 , l b ≤ x ≤ u b 。 \qquad\qquad\qquad\qquad\qquad s.t.\begin{cases} A\cdot x\leq b,\\ Aeq\cdot x=beq,\\ c(x)\leq 0,\\ ceq(x)=0,\\ lb\leq x\leq ub。\end{cases} s.t.⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧A⋅x≤b,Aeq⋅x=beq,c(x)≤0,ceq(x)=0,lb≤x≤ub。
的Matlab命令为
[ x , f v a l ] = f m i n i m a x ( f u n , x 0 , A , b , A e q , b e q , l b , u b , n o n l c o n , o p t i o n s ) [x,fval]=fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) [x,fval]=fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
例 求函数族{ f 1 ( x ) , f 2 ( x ) , f 3 ( x ) , f 4 ( x ) , f 5 ( x ) f_1(x),f_2(x),f_3(x),f_4(x),f_5(x) f1(x),f2(x),f3(x),f4(x),f5(x)}取极小——极大值时的 x x x值,其中
{ f 1 ( x ) = 2 x 1 2 + x 2 2 − 48 x 1 − 40 x 2 + 304 , f 2 ( x ) = − x 1 2 − 3 x 2 2 , f 3 ( x ) = x 1 + 3 x 2 − 18 , f 4 ( x ) = − x 1 − x 2 , f 5 ( x ) = x 1 + x 2 − 8 。 \qquad\qquad\qquad\qquad\qquad \begin{cases} f_1(x)=2x_1^2+x_2^2-48x_1-40x_2+304,\\ f_2(x)=-x_1^2-3x_2^2,\\ f_3(x)=x_1+3x_2-18,\\ f_4(x)=-x_1-x_2,\\ f_5(x)=x_1+x_2-8。\end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧f1(x)=2x12+x22−48x1−40x2+304,f2(x)=−x12−3x22,f3(x)=x1+3x2−18,f4(x)=−x1−x2,f5(x)=x1+x2−8。
解 (1)编写M函数fun9.m定义向量函数如下:
function f=fun9(x);
f=[2*x(1)^2+x(2)^2-48*x(1)-40*x(2)+304
-x(1)^2-3*x(2)^2
x(1)+3*x(2)-18
-x(1)-x(2)
x(1)+x(2)-8];
(2)调用函数 f m i n i m a x fminimax fminimax:
[x,y]=fminimax(@fun9,rand(2,1))
求得 x 1 x_1 x1=4, x 2 x_2 x2=4,对应的 f 1 ( x ) f_1(x) f1(x)=0, f 2 ( x ) f_2(x) f2(x)=-64, f 3 ( x ) f_3(x) f3(x)=-2, f 4 ( x ) f_4(x) f4(x)=-8, f 5 ( x ) f_5(x) f5(x)=0。
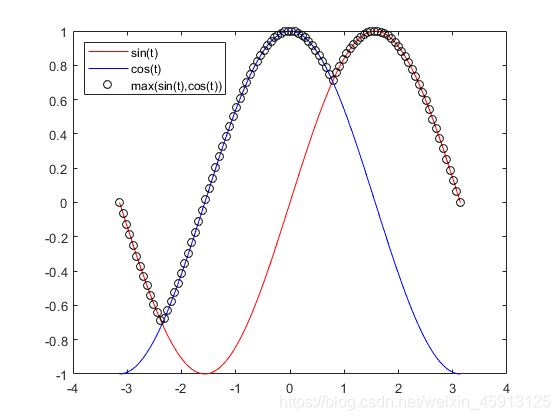
该图就相当于求{ s i n x , c o s x sinx,cosx sinx,cosx}的极小——极大值。
圆圈即该方程组的极大值,求的极小值即圆圈曲线的极小值。