阅读笔记-Iterative Refinement in the Continuous Spacefor Non-Autoregressive Neural Machine Translation

尽管自回归序列建模最近取得了成功，但由于其序列处理的性质，它存在弱点。当我们试图从一个训练过的模型中解码最有可能的序列时，这个弱点就会显现出来.没有已知的多项式算法来精确地解决它，从业者依赖近似解码算法。其中，波束搜索因其优于贪心译码的性能而成为选择的方法，但贪心译码带来了大量的计算开销。

我们的随机迭代目标增强方法，如图2所示，建立在评估候选分子的性质比生成这些分子更容易的思想之上。因此，一个学习过的属性预测器可以用来有效地指导生成过程。为了实现这一想法，我们的方法首先在一个小型监督数据集上预先训练生成模型和属性预测器。属性预测器然后作为一个可能性模型过滤候选分子从生成模型。通过此筛选的候选代成为pa

两个任务：分子生成，图到图的分子改进

给定输入X生成Y，其中Y要符合一些约束比如生成的Y在某些性质上足够高，以及和X足够相似。由此得到了数据集$\mathcal{D}=\left\{(X_i,Y_i)\right\}$
Augmentation Step：$\mathcal{D}$是原始数据集。${\mathcal{D}}_t$是第t次迭代时的数据集。先用$X_i\in \mathcal{D}$输入模型得到$C$个候选翻译示例$Y_i^1,..,Y_i^C$。我们将其中满足约束的前K个样本选出来，并加入${\mathcal{D}}_{t+1}$。当我们找不到K个不同的有效翻译时，我们只需将原始翻译Yi的副本添加到Dt+1中以保持平衡。
过程如下：

Training Step：得到新的数据集${\mathcal{D}}_{t+1}$来训练${\mathcal{P}}^{(t)}$。
上述训练过程在算法1中进行了总结。由于约束c是先验已知的，因此我们可以构造一个外部属性过滤器以去除在Augmentation Step中违反c的生成的输出。 在测试时，我们还使用此过滤器来筛选预测的输出。 为了提出给定输入X的最终转换，我们从模型中采样多达L个输出，直到找到满足约束c的输出为止。 如果所有L次样本均因特定输入而失败，则我们输出失败样本中的第一个。
模型可以被称为随机期望最大化算法。 $c$是一个二进制随机变量，它的值是X与Y的函数，代表着生成的Y是否满足关于X的期望的约束。即生成的Y为$Y\in B(X)\frac{def}{=}\left\{Y^{{}^{\prime }}:c=1|X,Y^{{}^{\prime }}\right\}$。
如果初始的翻译模型$P^{(0)}(Y|X)$对于任何给定的输入X，作为一个相对于输出Y的合理的先验分布，我们可以简单地反转过滤器并使用下式作为理想的翻译模式。并且概率p(c= 1|X,Y)要么是0要么是1，因为c是X和Y的函数。这种后验计算通常是不可行的，但可以通过抽样进行近似;尽管如此，它还是很大程度上依赖于先验$P^{(0)}(Y|X)$的适当性。相反，我们更进一步，迭代地优化参数化定义的先验平移模型$P_{\theta }^{(0)}(Y|X)$。我们将对数可能性最大化，即候选翻译满足过滤器中隐式编码的约束：

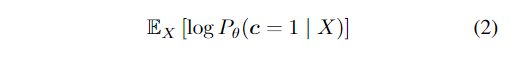
在许多情况下，任何给定输入X都有多个可行的输出。训练数据可能仅提供其中一个（或不提供）。 因此，我们将输出结构Y视为潜变量，并扩展Eq(2)的内部项：

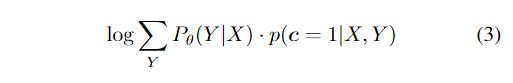
在我们的方法中， augmentation step是E-step的采样版本，在该步骤中，通过滤波器引导的拒绝采样来提取后验样本。样本数K控制着后验近似的质量。基于增强目标的附加训练步骤对应于广义M-step（尽管由于随机性不能保证改善）。
$P_{\theta }^{(t)}(Y|X)$是t期强化训练后的当前翻译模型。在第 t+ 1个epoch中， augmentation step首先使用由θ（t）参数化的旧模型P（t）为每个输入X采样C个不同的候选项，然后删除违反约束c的那些候选项,其余的候选样本可解释为当前后验的样本。因此，训练步骤通过随机梯度下降使EM辅助目标最大化：

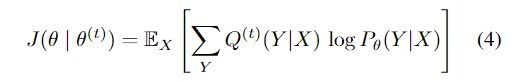
我们对模型进行多次迭代训练，并通过经验证明，在主要实验以及附录B中的玩具模型中，随着添加更多迭代，模型的性能确实会不断提高。EM方法可能会收敛到一个不同且更好的模型 性能模型，而不是公式1中讨论的初始后验计算。

实验

Conditional Molecular Design

条件分子设计的目标是修饰分子以改善其化学性质。如图1所示，条件分子设计被表述为一个图到图的转换问题。训练数据是一组分子对$\mathcal{D}=\left\{(X_i,Y_i)\right\}$。X是输入前体，Y是具有改进特性的相似分子。 每个分子进一步用其性能评分标记。 我们的方法非常适合条件分子设计，因为目标分子不是唯一的：可以以多种不同的方式修饰每种前体以优化其性能。 因此，我们可以在数据扩充期间为每个前体发现几个新目标。
约束c分为两个部分:

• Y的化学性质必须超过某个阈值β
• X和Y之间的分子相似性必须超过一定的阈值
  分子相似性sim(X,Y)定义为摩根指纹的Tanimoto相似性，它测量两个分子之间的结构重叠。
  在实际环境中，经常通过实验分析来评估化学性质的基本真值，而对于随机迭代的目标扩增而言，这种方法过于昂贵且费时。 因此，我们在计算机属性预测器F_1中构造一个代理，以近似真实属性评估器F0。 为了训练该代理预测变量，我们使用训练集中的分子及其标记的属性值。 代理预测变量F1被参数化为图卷积网络，并使用Chemprop软件包进行训练。 在数据扩充过程中，我们使用F_1筛选出预测特性得分低于阈值β的分子。
  两个分子设计任务：
• QED 优化：任务是改善给定化合物X的药物相似性（QED）
• DRD2 优化：其任务是优化针对多巴胺2型受体的生物活性。

评价指标：

• Success：分子X的任何输出Y1 … YZ都满足要求的相似性和属性约束（先前为每个任务指定）的分数。这是我们的主要指标
• Diversity：对于每个分子X，我们测量Y1 … YZ中一组成功翻译的化合物对之间的平均Tanimoto距离（定义为1-sim（Yi，Yj））。 如果成功翻译次数少于或少于一次，则分集为0。我们在所有测试前体X上平均此数量。

作者使用了两种模型来评估他们的方法：

• VSeq2Seq
• HierGNN