矩阵分解

煮个栗子先

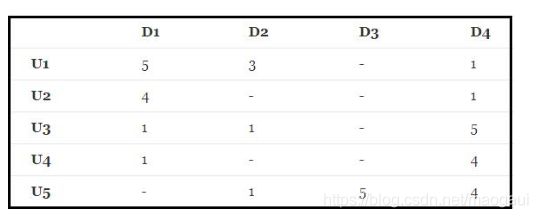
——矩阵分解的思想可以解决这个问题，其实这种思想可以看作是有监督的机器学习问题（回归问题）。

矩阵R可以近似表示为P与Q的乘积：R（n,m）≈ P(n,K)*Q(K,m)

矩阵分解的过程中，将原始的评分矩阵分解成两个矩阵和的乘积：

矩阵P(n,K)表示n个user和K个特征之间的关系矩阵，这K个特征是一个中间变量，矩阵Q(K,m)的转置是矩阵Q(m,K)，矩阵Q(m,K)表示m个item和K个特征之间的关系矩阵，这里的K值是自己控制的，可以使用交叉验证的方法获得最佳的K值。为了得到近似的R(n,m)，必须求出矩阵P和Q，如何求它们呢？

【方法】
1.首先令
2.损失函数：使用原始的评分矩阵与重新构建的评分矩阵之间的误差的平方作为损失函数，即：
如果R(i,j)已知，则R(i,j)的误差平方和为：
最终，需要求解所有的非“-”项的损失之和的最小值：
3.使用梯度下降法获得修正的p和q分量：
求解损失函数的负梯度：
根据负梯度的方向更新变量：
4.不停迭代直到算法最终收敛（直到sum(e^2) <=阈值）
（Plus：为了防止过拟合，增加正则化项）
【加入正则项的损失函数求解】
1.首先令
2.通常在求解的过程中，为了能够有较好的泛化能力，会在损失函数中加入正则项，以对参数进行约束，加入正则的损失函数为：
也即：

   3.使用梯度下降法获得修正的p和q分量：
      求解损失函数的负梯度：
      根据负梯度的方向更新变量：
   4.不停迭代直到算法最终收敛（直到sum(e^2) <=阈值）

【预测】利用上述的过程，我们可以得到矩阵和，这样便可以为用户 i 对商品 j 进行打分：
【Python代码实现如下】（基于Python 3.X ；使用正则项）

# !/usr/bin/env python
# encoding: utf-8
__author__ = 'Scarlett'
#矩阵分解在打分预估系统中得到了成熟的发展和应用
# from pylab import *
import matplotlib.pyplot as plt
from math import pow
import numpy


def matrix_factorization(R,P,Q,K,steps=5000,alpha=0.0002,beta=0.02):
    Q=Q.T  # .T操作表示矩阵的转置
    result=[]
    for step in range(steps):
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j]>0:
                    eij=R[i][j]-numpy.dot(P[i,:],Q[:,j]) # .dot(P,Q) 表示矩阵内积
                    for k in range(K):
                        P[i][k]=P[i][k]+alpha*(2*eij*Q[k][j]-beta*P[i][k])
                        Q[k][j]=Q[k][j]+alpha*(2*eij*P[i][k]-beta*Q[k][j])
        eR=numpy.dot(P,Q)
        e=0
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j]>0:
                    e=e+pow(R[i][j]-numpy.dot(P[i,:],Q[:,j]),2)
                    for k in range(K):
                        e=e+(beta/2)*(pow(P[i][k],2)+pow(Q[k][j],2))
        result.append(e)
        if e<0.001:
            break
    return P,Q.T,result

if __name__ == '__main__':
    R=[
        [5,3,0,1],
        [4,0,0,1],
        [1,1,0,5],
        [1,0,0,4],
        [0,1,5,4]
    ]

    R=numpy.array(R)

    N=len(R)
    M=len(R[0])
    K=2

    P=numpy.random.rand(N,K) #随机生成一个 N行 K列的矩阵
    Q=numpy.random.rand(M,K) #随机生成一个 M行 K列的矩阵

    nP,nQ,result=matrix_factorization(R,P,Q,K)
    print("原始的评分矩阵R为：\n",R)
    R_MF=numpy.dot(nP,nQ.T)
    print("经过MF算法填充0处评分值后的评分矩阵R_MF为：\n",R_MF)

#-------------损失函数的收敛曲线图---------------

    n=len(result)
    x=range(n)
    plt.plot(x,result,color='r',linewidth=3)
    plt.title("Convergence curve")
    plt.xlabel("generation")
    plt.ylabel("loss")
    plt.show()