基于模拟退火算法的TSP算法

一，理论基础

模拟退火(simulated annealing,SA)算法的思想最早是由Metropolis等提出的。其出发点是基于物理中固体物质的退火过程与一般的组合优化问题之间的相似性。模拟退火法是一种通用的优化算法，其物理退火过程由以下三部分组成：
（1）加温过程。其目的是增强粒子的热运动，使其偏离平衡位置。当温度足够高时，固体将熔化为液体，从而消除系统原先存在的非均匀状态。
（2）等温过程。对于与周围环境交换热量而温度不变的封闭系统，系统状态的自发变化总是朝自由能减少的方向进行的，当自由能达到最小时，系统达到平衡状态。
（3）冷却过程。使粒子热运动减弱，系统能量下降，得到晶体结构。
SA算法实现过程如下（以最小化问题为例）：
（1）初始化：取初始温度$T_0$足够大，令$T=T_0$，任取初始解$S_1$，确定每个$T$时的迭代次数，即Metropolis链长$L$。
（2）对当前温度$T$和$k=1,2,\cdots ,L$，重复步骤(3)~(6)。
（3）对当前解$S_1$随机扰动(比如交换$S_1$分量的数据)产生一个新解$S_2$。
（4）计算S2的增量$df=f(S_2)-f(S_1)$，其中$f(S_1)$为S1的代价函数。
（5）若$df<0$，则接受S2作为新的当前解，即$S_1=S_2$；否则计算S2的接受概率$exp(-df/T)$，即随机产生$(0,1)$区间上均匀分布的随机数$rand$，若$exp(-df/T)>rand$，也接受S2作为新的当前解，$S_1=S_2$；否则保留当前解$S_1$。
（6）如果满足终止条件$Stop$，则输出当前解$S_1$为最优解，结束程序。终止条件$Stop$通常为：在连续若干个Metropolis链中新解$S_2$都没有被接受时终止算法，或是设定结束温度。否则，则按衰减函数衰减$T$后返回步骤（2）。
以上步骤称为Metropolis过程。逐渐降低控制温度，重复Metropolis过程，直至满足结束准则Stop，求出最优解。

二，TSP问题介绍

TSP(traveling salesman problem,旅行商问题)是典型的NP完全问题，即其最坏情况下的时间复杂度随着问题规模的增大按指数方式增长，到目前为止还未找到一个多项式时间的有效算法。
TSP问题可描述为：已知$n$个城市相互之间的距离，某一旅行商从某个城市出发访问每个城市有且仅有一次，最后回到出发城市，如何安排才使其所走路线距离最短。简言之，就是寻找一条最短的遍历$n$个城市的路径，或者说搜索自然子集$X=\{1,2,\cdots ,n\}$($X$的元素表示对$n$个城市的编号)的一个排列$\pi (X)=\{V_1,V_2,\cdots ,V_n\}$，使得$$T_d=\sum _{i=1}^{n+1}d(V_i,V_{i+1})+d(V_n,V_1)$$取得最小值，其中$d(V_i,V_{i+1})$表示城市$V_i$到城市$V_{i+1}$的距离。

三，思路和步骤

1.算法流程
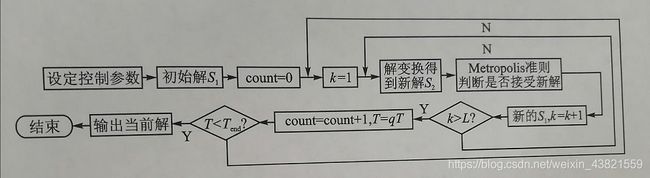
模拟退火算法求解TSP问题的流程图如图1所示。

图1 模拟退火算法求解流程图

2.模拟退火算法实现

控制参数的设置

需要设置的主要控制参数有降温速率$q$、初始温度$T_0$、结束温度$T_{end}$以及链长$L$。

初始解

对于$n$个城市的TSP问题，得到的解就是对1~$n$的一个排序，其中每个数字对应城市的编号。

解变换生成新解

通过对当前解$S_1$进行变换，产生新的路径数组即新解，这里采用的变换是产生随机数的方法来产生将要交换的两个城市，用二邻域变换法产生新的路径，即可行的新解$S_2$。

Metropolis准则

若路径长度函数为$f(S)$，则当前解的路径为$f(S_1)$，新解的路径为$f(S_2)$，路径差为$df=f(S_2)-f(S_1)$，则Metropolis准则为$$P=\{\begin{array}{ll}1,& \text{df<0}\\ exp(-\frac{df}{T}),& \text{df≥0}\end{array}$$如果$df<0$，则以概率1接受新的路径；否则以概率$exp(-\frac{df}{T})$接受新的路径。

降温

利用降温速率$q$进行降温，即$T=qT$，若$T$小于结束温度，则停止迭代输出当前状态，否则继续迭代。

四，MATLAB程序实现

• 计算距离矩阵

function D = Distance(citys)
%% 计算两两城市之间的距离
% 输入 citys  各城市的位置坐标
% 输出 D  两两城市之间的距离

n = size(citys,1);
D = zeros(n,n);
for i = 1:n
   for j = i+1:n
       D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
       D(j,i) = D(i,j);
   end
end

• 初始解

S1=randperm(N);			% 随机产生一个初始路线

• 生成新解

function S2 = NewAnswer(S1)
%% 输入
% S1:当前解
%% 输出
% S2：新解

N = length(S1);
S2 = S1;                
a = round(rand(1,2)*(N-1)+1); %产生两个随机位置 用来交换
W = S2(a(1));
S2(a(1)) = S2(a(2));
S2(a(2)) = W;         %得到一个新路线

• Metropolis准则

function [S,R] = Metropolis(S1,S2,D,T)
%% 输入
% S1：  当前解
% S2:   新解
% D:    距离矩阵（两两城市的之间的距离）
% T:    当前温度
%% 输出
% S：   下一个当前解
% R：   下一个当前解的路线距离

R1 = PathLength(D,S1);  %计算路线长度
N = length(S1);         %得到城市的个数

R2 = PathLength(D,S2);  %计算路线长度
dC = R2 - R1;   %计算能力之差
if dC < 0       %如果能力降低 接受新路线
    S = S2;
    R = R2;
elseif exp(-dC/T) >= rand   %以exp(-dC/T)概率接受新路线
    S = S2;
    R = R2;
else        %不接受新路线
    S = S1;
    R = R1;
end

• 画路线轨迹图

function DrawPath(Route,citys)
%% 画路径函数
%输入
% Route  待画路径   
% citys  各城市坐标位置

figure
plot([citys(Route,1);citys(Route(1),1)],...
     [citys(Route,2);citys(Route(1),2)],'o-');
grid on

for i = 1:size(citys,1)
    text(citys(i,1),citys(i,2),['   ' num2str(i)]);
end

text(citys(Route(1),1),citys(Route(1),2),'       起点');
text(citys(Route(end),1),citys(Route(end),2),'       终点');

• 输出路径函数

function p = OutputPath(R)
%% 输出路径函数
% 输入：R 路径
R = [R,R(1)];
N = length(R);
p = num2str(R(1));
for i = 2:N
    p = [p,'—>',num2str(R(i))];
end
disp(p)

• 可行解路线长度函数

function Length = PathLength(D,Route)
%% 计算各个体的路径长度
% 输入：
% D     两两城市之间的距离
% Route 个体的轨迹

Length = 0;
n = size(Route,2);
for i = 1:(n - 1)
    Length = Length + D(Route(i),Route(i + 1));
end
Length = Length + D(Route(n),Route(1));

• 模拟退火算法主函数
  模拟退火算法参数设置如下所列。

主函数代码如下：

 %% I. 清空环境变量
clear all
clc

%% II. 导入城市位置数据
X = [16.4700   96.1000
     16.4700   94.4400
     20.0900   92.5400
     22.3900   93.3700
     25.2300   97.2400
     22.0000   96.0500
     20.4700   97.0200
     17.2000   96.2900
     16.3000   97.3800
     14.0500   98.1200
     16.5300   97.3800
     21.5200   95.5900
     19.4100   97.1300
     20.0900   92.5500];

%% III. 计算距离矩阵
D = Distance(X);  %计算距离矩阵
N = size(D,1);    %城市的个数

%% IV. 初始化参数
T0 = 1e10;   % 初始温度
Tend = 1e-30;  % 终止温度
L = 2;    % 各温度下的迭代次数
q = 0.9;    %降温速率
syms x;
Time = ceil(double(solve(T0*(0.9)^x == Tend)));    % 计算迭代的次数
% Time = 132;
count = 0;        %迭代计数
Obj = zeros(Time,1);         %目标值矩阵初始化
track = zeros(Time,N);       %每代的最优路线矩阵初始化

%% V. 随机产生一个初始路线
S1 = randperm(N);
DrawPath(S1,X)
disp('初始种群中的一个随机值:')
OutputPath(S1);
Rlength = PathLength(D,S1);
disp(['总距离：',num2str(Rlength)]);

%% VI. 迭代优化
while T0 > Tend
    count = count + 1;     %更新迭代次数
    temp = zeros(L,N+1);
    %%
    for k = 1:L
        % 1. 产生新解
        S2 = NewAnswer(S1);
        % 2. Metropolis法则判断是否接受新解
        [S1 R] = Metropolis(S1, S2, D, T0);   % Metropolis抽样算法
        temp(k, :) = [S1 R];            % 记录下一路线及其长度
    end
    %% 3. 记录每次迭代过程的最优路线
    [d0, index] = min(temp(:, end));    % 找出当前温度下最优路线
    if count == 1 || d0 <= Obj(count-1)
        Obj(count) = d0;                    % 如果当前温度下最优路程小于上一路程则记录当前路程
    else
        Obj(count) = Obj(count-1);    % 如果当前温度下最优路程大于上一路程则记录上一路程
    end
    track(count, :) = temp(index, 1:end-1);  % 记录当前温度的最优路线
    %降温
    T0 = q * T0;
end

%% VII. 优化过程迭代图
figure
plot(1:count,Obj)
xlabel('迭代次数')
ylabel('距离')
title('优化过程')

%% VIII. 绘制最优路径图
DrawPath(track(end,:),X)

%% IX. 输出最优解的路线和总距离
disp('最优解:')
S = track(end,:);
p = OutputPath(S);
disp(['总距离：',num2str(PathLength(D,S))]);

五，结果分析

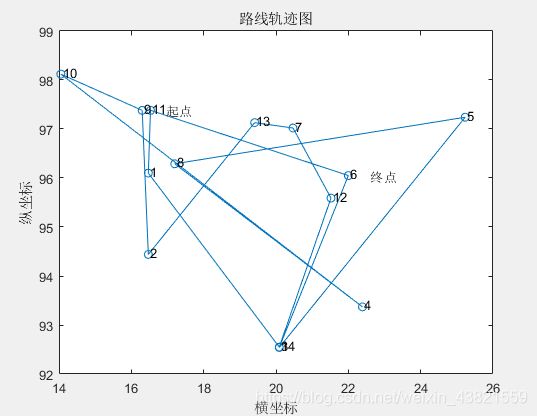
优化前的一个随机路线轨迹图如图2所示。

初始种群中的一个随机值:
11—>1—>14—>12—>7—>13—>2—>9—>10—>4—>8—>5—>3—>6—>11
总距离：62.0785

优化后的路线如图3所示。

最优解:
6—>12—>7—>13—>8—>11—>9—>10—>1—>2—>14—>3—>4—>5—>6
总距离：29.3405

图2 随机路线图

图3 最优解路线图

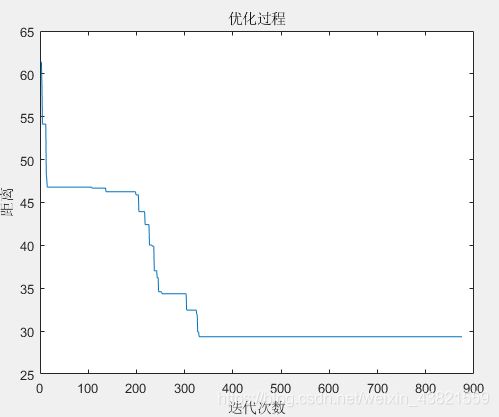
优化迭代过程如图4所示。

图4 模拟退火算法优化过程图

由图4可以看出，优化前后路径长度得到很大改进，由优化前的64.7606变为29.8332，变为原来的46.1%，600多代以后路径长度已经保持不变了，可以认为已经是最优解了。

六，算法的改进

（1）使用逆转操作，即选择两个城市后，逆转这两个城市之间的所有城市。
（2）选择3个城市，将两个城市之间的城市插入到第3个城市的后面(这两个城市之间不包括第3个城市)。

七，算法的局限性

问题规模$n$比较小时，得到的一般都是最优解，但当规模比较大时，一般只能得到近似解。这时可以通过增大种群大小和增加最大迭代次数使优化值更接近最优解。

八，参考文献

[1] 张建航, 李国. 模拟退火算法及其在求解TSP中的应用[J]. 现代电子技术, 2006, 29(22): 157-158.
[2] 盛国华, 陈玉金. 改进模拟退火算法求解TSP问题[J]. 电脑知识与技术, 2008(15): 129-130+156.
[3] 郁磊, 史峰, 王辉, 等. MATLAB智能算法30个案例分析(第2版)[M]. 北京: 北京航空航天大学出版社, 2015.