机器学习基础(6)—— 使用权重衰减和丢弃法缓解过拟合问题
- 参考:动手学深度学习
- 注:本文是 jupyter notebook 文档转换而来,部分代码可能无法直接复制运行!
- 关于过拟合问题的详细说明请见:机器学习基础(3)—— 泛化能力、过拟合与欠拟合
文章目录
- 1. 权重衰减
-
- 1.1 原理
- 1.2 实验
-
- 1.2.1 手动实现
- 1.2.2 利用 Pytorch 简洁实现
- 2. 丢弃法
-
- 2.1 原理
- 2.2 实验
-
- 2.2.1 手动实现
- 2.2.2 利用 Pytorch 简洁实现
1. 权重衰减
1.1 原理
-
权重衰减等价于L2正则化。正则化是一种基于“策略”的模型选择方法,是结构风险最小化策略 SRM 的实现,通过在经验风险最小化上增加一个正则化项regularizer/罚项penalty item,使得优化后得到的模型的经验风险和复杂度同时小,避免过拟合稍微多讲一点原理
- 我们知道,模型复杂度相对样本复杂度过高时就会出现过拟合,一个没有任何约束的全连接 MLP 网络是复杂度最高的,需要最多数据训练,很容易因数据复制度相对低导致过拟合(从另一方面讲,这样的网络容量最大,表示能力最强,数据充分多时性能上限也是最高的)
- 降低网络尺寸是减小网络容量最简单的做法,但这种 naive 的方式效果不怎么好
- L2 正则化、权重衰减和 dropout 本质上都是稍微高级一点的减少网络复杂度的方式,它们基本都是给网络加上了一个 “让网络参数的平方范数小一点” 的约束,以免参数中出现极大值主导网络输出。除了这些以外还有一些其他的正则化方法,总之只要是通用的减少模型复杂度的方法,一般都称为
正则化 regularization,到处都可以用 - 对网络结构的修改也可以看作对 MLP 增加约束来减少网络复杂度(网络容量),从这个角度看,CNN, Transformer 这些复杂的网络结构都可以看作 MLP 以特定方式减少容量后的结果,而这个约束方式(网络结构)是基于被处理的数据特点而专门设计的。换句话说,虽然这时模型容量降低了,但是提取这些特定数据特征的能力并没有下降太多,这样就能用更少的数据学到更好的结果。这种针对被处理数据特性而进行的,通过修改网络结构,有针对性地减少模型复杂度的 “正则化” 方法,称为
模型的归纳偏置 model bias - 很多论文中,作者会在损失函数中提出自己的正则化项,本质上基本都可以理解为:作者注意到了问题或数据的一些潜在特点,于是通过向损失中增加正则化项,来针对性地、隐式地约束网络优化方向,从而限制网络结构,减少网络容量,增强模型的归纳偏置
-
L2正则化对模型原始损失添加了一个 L 2 L_2 L2 范数惩罚项。对于一个普通的线性回归问题,原始损失为
l ( w 1 , w 2 , b ) = 1 n ∑ i = 1 n 1 2 ( x 1 ( i ) w 1 + x 2 ( i ) w 2 + b − y ( i ) ) 2 \mathcal{l}(w_1,w_2,b) = \frac{1}{n}\sum_{i=1}^n\frac{1}{2}(x_1^{(i)}w_1+x_2^{(i)}w_2+b-y^{(i)})^2 l(w1,w2,b)=n1i=1∑n21(x1(i)w1+x2(i)w2+b−y(i))2将参数表示为权重向量 w = [ w 1 , w 2 ] \pmb{w}=[w_1,w_2] www=[w1,w2],增加 L 2 L_2 L2 范数惩罚项,得到新的损失函数为
l ( w 1 , w 2 , b ) + λ 2 n ∣ ∣ w ∣ ∣ 2 \mathcal{l}(w_1,w_2,b) + \frac{\lambda}{2n}||\pmb{w}||^2 l(w1,w2,b)+2nλ∣∣www∣∣2
其中 λ > 0 \lambda>0 λ>0 用来控制惩罚项的作用程度,用来控制经验风险和模型复杂度之间的权衡。这种情况下随机梯度下降的迭代公式变成
w i ← w i − η ∣ B ∣ ∑ i ∈ B x i ( i ) ( x 1 ( i ) w 1 + x 2 ( i ) w 2 + b − y ( i ) ) − η λ ∣ B ∣ w i = ( 1 − η λ ∣ B ∣ ) w i − η ∣ B ∣ ∑ i ∈ B x i ( i ) ( x 1 ( i ) w 1 + x 2 ( i ) w 2 + b − y ( i ) ) \begin{aligned} w_i \leftarrow & w_i -\frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} x_i^{(i)}\left(x_1^{(i)} w_1+x_2^{(i)} w_2+b-y^{(i)}\right)- \frac{\eta \lambda}{|\mathcal{B}|} w_i\\ = &\left(1-\frac{\eta \lambda}{|\mathcal{B}|}\right) w_i-\frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} x_i^{(i)}\left(x_1^{(i)} w_1+x_2^{(i)} w_2+b-y^{(i)}\right) \end{aligned} wi←=wi−∣B∣ηi∈B∑xi(i)(x1(i)w1+x2(i)w2+b−y(i))−∣B∣ηλwi(1−∣B∣ηλ)wi−∣B∣ηi∈B∑xi(i)(x1(i)w1+x2(i)w2+b−y(i))可见, L 2 L_2 L2 正则化中权重 w i w_i wi 先乘以小于 1 的数,再减去原版不含惩罚项损失的梯度,因此 L 2 L_2 L2 范数又称为
权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制,这可能对过拟合有效 -
实际场景中,我们有时也将惩罚项设置为偏差元素的平方和(即把上面惩罚项中的 ∣ B ∣ |\mathcal{B}| ∣B∣ 去掉),迭代公式为
w i = ( 1 − η λ ) w i − η ∣ B ∣ ∑ i ∈ B x i ( i ) ( x 1 ( i ) w 1 + x 2 ( i ) w 2 + b − y ( i ) ) w_i = \left(1-\eta \lambda\right) w_i-\frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} x_i^{(i)}\left(x_1^{(i)} w_1+x_2^{(i)} w_2+b-y^{(i)}\right) wi=(1−ηλ)wi−∣B∣ηi∈B∑xi(i)(x1(i)w1+x2(i)w2+b−y(i))
1.2 实验
-
首先设计一个高维线性回归问题来造成过拟合,再观察使用权重衰减后对过拟合问题的缓解效果。如下生成训练样本
y = 0.05 + ∑ i = 1 p 0.01 x i + ϵ y = 0.05+\sum_{i=1}^p 0.01x_i+\epsilon y=0.05+i=1∑p0.01xi+ϵ 其中 ϵ ∼ N ( 0 , 0.01 ) \epsilon\sim N(0,0.01) ϵ∼N(0,0.01) 是高斯采样误差,前面部分是回归的目标函数, p p p 是样特征数(问题维度)。为了造成过拟合,我们通过如下两步使模型复杂度相对样本复杂度过高- 使用维度和问题维度相同的模型,将问题维度调高使模型复杂,使 p = 200 p=200 p=200
- 样本复杂度尽量低,减少训练样本数量,使 n = 20 n=20 n=20
%matplotlib inline import numpy as np import math import scipy.stats as st import matplotlib.pylab as plt import numpy as np from scipy import stats import torch import random from IPython import display import matplotlib # 真实参数 n_train, n_test, num_inputs = 20, 100, 200 true_w, true_b = torch.ones(num_inputs, 1)*0.01, 0.05 # 构造样本集(训练集和测试集) features = torch.randn((n_train + n_test, num_inputs)) labels = torch.matmul(features, true_w) + true_b labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float) train_features, test_features = features[:n_train, :], features[n_train:, :] train_labels, test_labels = labels[:n_train], labels[n_train:]
1.2.1 手动实现
-
手动实现带线性回归,在损失函数后增加 L 2 L_2 L2 范数惩罚项来实现权重衰减
# matplotlib 处理负号无法显示的问题 matplotlib.rcParams.update( { 'text.usetex': False, 'font.family': 'stixgeneral', 'mathtext.fontset': 'stix', } ) batch_size, num_epochs, lr = 1, 100, 0.003 dataset = torch.utils.data.TensorDataset(train_features, train_labels) train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True) # 绘图函数,在一张图中绘制两条曲线,用来对比训练损失和验证损失的变化过程,观察过拟合 def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None, legend=None, semilogy=True, figsize=(3.5, 2.5)): # 设置图像尺寸 display.set_matplotlib_formats('svg') # Use svg format to display plot in jupyter fig = plt.figure(figsize = figsize) #plt.rcParams['figure.figsize'] = figsize # 坐标轴文本 plt.xlabel(x_label) plt.ylabel(y_label) # 绘制第一组数据 if semilogy: plt.semilogy(x_vals, y_vals) # y轴使用对数尺度的点线图 else: plt.plot(x_vals, y_vals) # 普通点线图 # 绘制第二组数据,y轴使用对数尺度的点线图(如果有的话) if x2_vals != None and y2_vals != None: if semilogy: plt.semilogy(x2_vals, y2_vals, linestyle=':') else: plt.plot(x2_vals, y2_vals, linestyle=':') plt.legend(legend) plt.show() def linreg(X, w, b): return torch.mm(X, w) + b def squared_loss(y_hat, y): # 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2 return ((y_hat - y.view(y_hat.size())) ** 2) / 2 def l2_penalty(w): return (w**2).sum() / 2 def sgd(params, lr, batch_size): for param in params: param.data -= lr * param.grad / batch_size def fit_and_plot(lambd): # 参数初始化 w = torch.randn((num_inputs, 1), requires_grad=True) b = torch.zeros(1, requires_grad=True) # 模型和损失 net = linreg loss = squared_loss # 训练 100 epoch,记录训练损失和测试损失变化 train_ls, test_ls = [], [] for _ in range(num_epochs): for X, y in train_iter: # 添加了L2范数惩罚项 l = loss(net(X, w, b), y) + lambd * l2_penalty(w) # 梯度清零 if w.grad is not None: w.grad.data.zero_() b.grad.data.zero_() # 计算梯度 l = l.sum() l.backward() # 随机梯度下降 sgd([w, b], lr, batch_size) # 记录损失 train_ls.append(loss(net(train_features, w, b), train_labels).mean().item()) test_ls.append(loss(net(test_features, w, b), test_labels).mean().item()) semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss', range(1, num_epochs + 1), test_ls, ['train', 'test']) # 观察最后得到模型参数的 L2 范数 print('L2 norm of w:', w.norm().item()) -
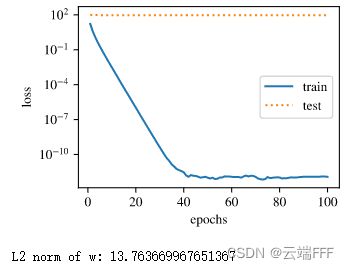
先看不使用权重衰减时的情况,设置参数
lambda=0,观察训练误差和验证误差随训练 epoch 的变化过程fit_and_plot(lambd=0)- 训练误差正常下降但测试误差一直很高,说明出现了过拟合
- 最终学出的 L 2 L_2 L2 范数较大,说明模型复杂度高
-
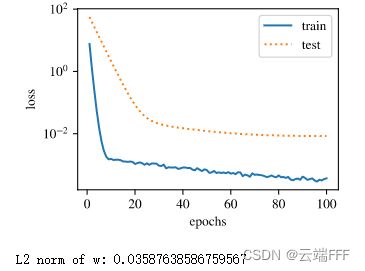
使用权重衰减,设置参数
lambda=3fit_and_plot(lambd=3)- 训练误差虽然有所提高,但测试集上的误差有所下降,过拟合现象得到一定程度的缓解
- 权重参数的 L 2 L_2 L2 范数比不使用权重衰减时更小,说明这时模型复杂度被控制
1.2.2 利用 Pytorch 简洁实现
-
pytorch 中的优化器有参数
weight_decay,可以直接设置权重衰减超参数 λ \lambda λ -
PyTorch 默认会对权重和偏置同时衰减,这里我们分别对权重和偏差构造优化器实例,从而只对权重衰减。只需修改上面的
fit_and_plot_pytorch函数def fit_and_plot_pytorch(wd): # 用一个全连接层作为线性模型,初始化参数 net = torch.nn.Linear(num_inputs, 1) torch.nn.init.normal_(net.weight, mean=0, std=1) torch.nn.init.normal_(net.bias, mean=0, std=1) # MSE 损失(pytorch 中在 loss 这里对 batch_size 取平均,下面优化器里不取平均) loss = torch.nn.MSELoss() # 权重和偏置用两个独立的优化器 optimizer_w = torch.optim.SGD(params=[net.weight], lr=lr, weight_decay=wd) # 对权重参数衰减 optimizer_b = torch.optim.SGD(params=[net.bias], lr=lr) # 不对偏差参数衰减 # 训练 100 epoch,记录训练损失和测试损失变化 train_ls, test_ls = [], [] for _ in range(num_epochs): for X, y in train_iter: # 梯度清零 optimizer_w.zero_grad() optimizer_b.zero_grad() # 反向传播计算梯度 l = loss(net(X), y).mean() l.backward() # 对两个optimizer实例分别调用step函数,从而分别更新权重和偏差 optimizer_w.step() optimizer_b.step() # 记录损失 train_ls.append(loss(net(train_features), train_labels).mean().item()) test_ls.append(loss(net(test_features), test_labels).mean().item()) semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss', range(1, num_epochs + 1), test_ls, ['train', 'test']) print('L2 norm of w:', net.weight.data.norm().item()) -
和 1.2.1 节一样,再次观察 γ = 0 \gamma=0 γ=0 不使用权重衰减和设置 γ = 3 \gamma=3 γ=3 使用权重衰减的情况
fit_and_plot_pytorch(0) fit_and_plot_pytorch(3)
2. 丢弃法
2.1 原理
-
丢弃法dropout是另一种深度学习模型常常使用的处理过拟合的方法,丢弃法有一些变体,这里特指倒置丢弃法inverted dropout -
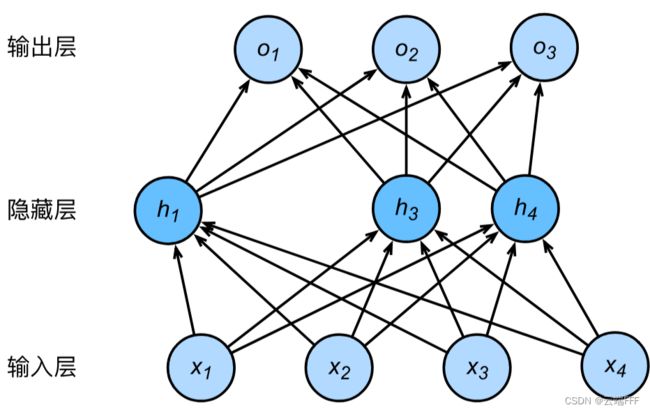
丢弃法的核心思想就是每轮训练随机去掉一些隐藏层单元,使得模型无法过于依赖某些特定的隐藏层单元,起到降低模型复杂度的作用。以有一个隐藏层的多层感知机为例,其原始结构为
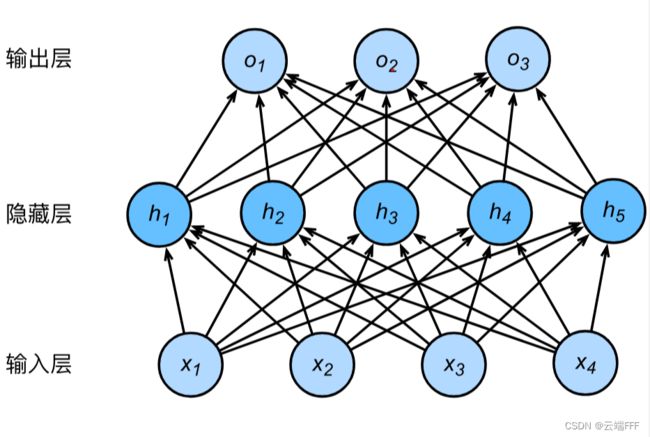
用 ϕ \phi ϕ 表示激活函数,任意隐藏层单元的输出 h i ( i = 1 , . . . , 5 ) h_i(i=1,...,5) hi(i=1,...,5) 为
h i = ϕ ( ∑ j = 1 4 x i w j i + b i ) h_i = \phi(\sum_{j=1}^4 x_iw_{ji}+b_i) hi=ϕ(j=1∑4xiwji+bi)当对该隐藏层使用丢弃法时,该层的隐藏单元将有一定概率被丢弃掉,丢弃概率是一个超参数,设为 p p p,则对于任意单元 i i i- 有 p p p 的概率此单元输出 h i h_i hi 被清零
- 有 1 − p 1-p 1−p 的概率此单元输出会除以 1 − p 1-p 1−p 进行放大
即该单元输出为
h i ′ = { 0 以 p 的 概 率 1 1 − p h i 以 1 − p 的 概 率 h_i'=\left\{ \begin{aligned} &0 & &以 \space p \space 的概率 \\ &\frac{1}{1-p}h_i & &以 \space 1-p\space 的概率 \end{aligned} \right. hi′=⎩⎪⎨⎪⎧01−p1hi以 p 的概率以 1−p 的概率显然有 E ( h i ′ ) = h i \mathbb{E}(h_i')=h_i E(hi′)=hi,即丢弃法不会改变任何隐藏层单元输出的期望值
-
dropout 有效的原因
- 直观上看,使用 dropout 会将原本较大较复杂的网络变成一个相对简单的网络,减少了网络参数,降低了模型的相对复杂度
- 另一种直观理解是,dropout 使得模型无法过于依赖某些特定的隐藏层单元,这样就不会给某些神经元赋予过大的权重,最终会产生收缩权重的平方范数的效果,类似 L2 正则化
-
两个应用 dropout 的技巧
- 含多个隐藏层的模型,通常把靠近输入层的丢弃概率设得小一点
- 为了拿到更加确定性的结果,测试模型时一般不使用丢弃法
2.2 实验
2.2.1 手动实现
- 构造一个含有两个全连接隐藏层的多层感知机,每个隐藏层输出为 256,ReLU 激活函数,做 softmax 回归来解决 Fashion-MNIST 分类任务。第一个隐藏层的丢弃概率设为0.2,把第二个隐藏层的丢弃概率设为0.5
- 注意测试阶段不使用 dropout,如果用了 Pytorch 提供的
nn.Dropout()和nn.BatchNorm2d等方法,可以用torch.nn.Module的.eval()和.train()方法model.eval():不启用 BatchNormalization 和 Dropout。此时pytorch会自动把 BN 和 DropOut 固定住,不会取平均,而是用训练好的值。不然的话,一旦 test 的 batch_size 过小,很容易就会因 BN 层导致模型 performance 损失较大;model.train():启用 BatchNormalization 和 Dropout。 在模型测试阶段使用 model.train() 让 model 变成训练模式,此时 dropout 和 batch normalization 的操作在训练时起到防止网络过拟合的问题
- 下面给出完整代码,可以直接复杂到 vscode 运行
import torch import torchvision import torchvision.transforms as transforms import numpy as np from IPython import display import matplotlib.pyplot as plt import matplotlib # 绘图相关 -------------------------------------------------------------------------------------------------- # matplotlib 处理负号无法显示的问题 matplotlib.rcParams.update( { 'text.usetex': False, 'font.family': 'stixgeneral', 'mathtext.fontset': 'stix', } ) # 绘图函数,在一张图中绘制两条曲线 def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None, legend=None, semilogy=True, figsize=(3.5, 2.5)): # 设置图像尺寸 display.set_matplotlib_formats('svg') # Use svg format to display plot in jupyter fig = plt.figure(figsize = figsize) #plt.rcParams['figure.figsize'] = figsize # 坐标轴文本 plt.xlabel(x_label) plt.ylabel(y_label) # 绘制第一组数据 if semilogy: plt.semilogy(x_vals, y_vals) # y轴使用对数尺度的点线图 else: plt.plot(x_vals, y_vals) # 普通点线图 # 绘制第二组数据,y轴使用对数尺度的点线图(如果有的话) if x2_vals != None and y2_vals != None: if semilogy: plt.semilogy(x2_vals, y2_vals, linestyle=':') else: plt.plot(x2_vals, y2_vals, linestyle=':') plt.legend(legend) plt.show() # 数据集相关 -------------------------------------------------------------------------------------------------- # 加载数据集,train_size 指定使用的数据量 def load_data_fashion_mnist(train_size, batch_size, num_workers=0, root='./Datasets/FashionMNIST'): mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True,transform=transforms.ToTensor()) mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True,transform=transforms.ToTensor()) train_iter = torch.utils.data.DataLoader(dataset=mnist_train, sampler=torch.utils.data.RandomSampler(mnist_train, replacement=True, num_samples=train_size), batch_size=batch_size, shuffle=False, num_workers=0) test_iter = torch.utils.data.DataLoader(dataset=mnist_test, batch_size=batch_size, shuffle=False, num_workers=0) # 这两个 iter 用来得到全部 train data 和 test data,访问一次即可 valid_train_iter = torch.utils.data.DataLoader(dataset=mnist_train, batch_size=train_size, shuffle=False, num_workers=0) valid_test_iter = torch.utils.data.DataLoader(dataset=mnist_test, batch_size=len(mnist_test), shuffle=False, num_workers=0) return train_iter, test_iter, valid_train_iter, valid_test_iter # 模型定义 -------------------------------------------------------------------------------------------------------- # 对某一层输出做 dropout 操作,其实就是把所有元素按上面 h' 公式原地更新一下 def dropout(X, drop_prob): # tensor 转换为 float 类型 X = X.float() # 用断言确保丢弃概率合法 assert 0 <= drop_prob <= 1 keep_prob = 1 - drop_prob # 这种情况下把全部元素都丢弃 if keep_prob == 0: return torch.zeros_like(X) # 以 keep_prob 概率生成一个过滤 mask,这里先得到 bool 型 tensor,然后用 .float 把元素转换为 1.0 和 0.0 mask = (torch.rand(X.shape) < keep_prob).float() return mask * X / keep_prob # 这里应用了广播机制 # 定义模型 drop_prob1, drop_prob2 = 0.2, 0.5 def net(X, is_training=True): # 每行一个样本特征 X = X.view(-1, num_inputs) # 第一个隐藏层,只在训练时使用丢弃法 H1 = (torch.matmul(X, W1) + b1).relu() if is_training: H1 = dropout(H1, drop_prob1) # 添加丢弃层 # 第二个隐藏层,只在训练时使用丢弃法 H2 = (torch.matmul(H1, W2) + b2).relu() if is_training: H2 = dropout(H2, drop_prob2) # 添加丢弃层 # 输出层返回 return torch.matmul(H2, W3) + b3 # 优化方法:小批量随机梯度下降 def sgd(params, lr, batch_size): for param in params: param.data -= lr * param.grad / batch_size # 注意这里更改 param 时用的param.data,这样不会影响梯度计算 # 评估模型(注意不进行 dropout 操作) def evaluate_accuracy(data_iter, net): acc_sum, n = 0.0, 0 for X, y in data_iter: # 使用 pytorch 模型 if isinstance(net, torch.nn.Module): # 评估模式, 这会关闭dropout net.eval() # 累计 batch 中预测对的样本数量 acc_sum += (net(X).argmax(dim=1) == y).float().sum().item() # 改回训练模式 net.train() # 自定义模型 else: # 如果 callable 对象 net 中有 is_training 这个参数 if('is_training' in net.__code__.co_varnames): # func.__code__.co_varnames 将函数局部变量以元组的形式返回。 acc_sum += (net(X, is_training=False).argmax(dim=1) == y).float().sum().item() # 将is_training设置成False else: acc_sum += (net(X).argmax(dim=1) == y).float().sum().item() # 总样本数 n += y.shape[0] return acc_sum / n # 模型训练 -------------------------------------------------------------------------------------------------------- def train(net, train_iter, test_iter, valid_train_iter, valid_test_iter, loss, num_epochs, batch_size, params=None, lr=None): # 拿到计算训练集 & 测试集损失的数据 for valid_train_X, valid_train_y in valid_train_iter: pass for valid_test_X, valid_test_y in valid_test_iter: pass train_size = len(valid_train_X) # 训练执行 num_epochs 轮 train_ls, test_ls = [], [] for epoch in range(num_epochs): train_l_sum = 0.0 # 本 epoch 总损失 train_acc_sum = 0.0 # 本 epoch 总准确率 n = 0 # 本 epoch 总样本数 for X, y in train_iter: # 计算小批量损失 y_hat = net(X, is_training=True) # 这里设置 is_training=False 则回到普通情况 l = loss(y_hat, y).mean() # 梯度清零 if params is not None and params[0].grad is not None: for param in params: param.grad.data.zero_() # 小批量的损失对模型参数求梯度 l.backward() # 做小批量随机梯度下降进行优化 sgd(params, lr, batch_size) # 手动实现优化算法 # 记录训练数据 train_l_sum += l.item() train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item() n += y.shape[0] # 训练完成一个 epoch 后,评估测试集上的准确率 test_acc = evaluate_accuracy(test_iter, net) # 训练损失 & 测试损失 trainls = loss(net(valid_train_X, is_training=False), valid_train_y).mean().item() testls = loss(net(valid_test_X, is_training=False), valid_test_y).mean().item() train_ls.append(trainls) test_ls.append(testls) # 打印提示信息 print('epoch %d, loss %.4f, tranin loss %.4f, test loss %.4f, train acc %.3f, test acc %.3f' % (epoch + 1, train_l_sum / (train_size/batch_size), trainls, testls, train_acc_sum / n, test_acc)) # 绘图 semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss', range(1, num_epochs + 1), test_ls, ['train', 'test']) if __name__ == '__main__': # 输入输出维度 num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256 # 初始化模型参数 & 设定超参数 W1 = torch.tensor(np.random.normal(0, 0.01, size=(num_inputs, num_hiddens1)), dtype=torch.float, requires_grad=True) b1 = torch.zeros(num_hiddens1, requires_grad=True) W2 = torch.tensor(np.random.normal(0, 0.01, size=(num_hiddens1, num_hiddens2)), dtype=torch.float, requires_grad=True) b2 = torch.zeros(num_hiddens2, requires_grad=True) W3 = torch.tensor(np.random.normal(0, 0.01, size=(num_hiddens2, num_outputs)), dtype=torch.float, requires_grad=True) b3 = torch.zeros(num_outputs, requires_grad=True) params = [W1, b1, W2, b2, W3, b3] num_epochs, lr = 10, 100.0 batch_size = 256 train_size = 60000 # 这个控制使用多少数据训练,最多 60000 # 获取数据读取迭代器 train_iter, test_iter, valid_train_iter, valid_test_iter = load_data_fashion_mnist(train_size, batch_size, 4) # 交叉熵损失 loss = torch.nn.CrossEntropyLoss() # 进行训练 train(net, train_iter, test_iter, valid_train_iter, valid_test_iter, loss, num_epochs, batch_size, params, lr) - 注意定义模型的
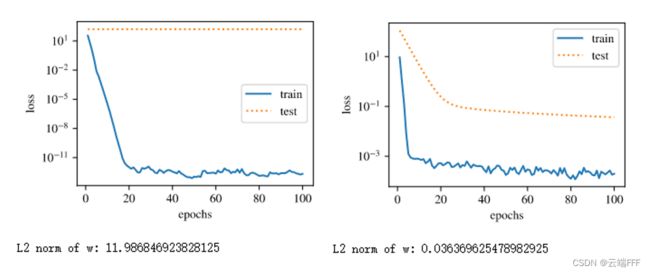
net函数,其中is_training参数用来控制是否在模型中加入 dropout 参数。下面左图在train函数中设置is_training=False来禁用 dropout,可见出现了一定的过拟合现象;右图使用 dropout,过拟合得到缓解
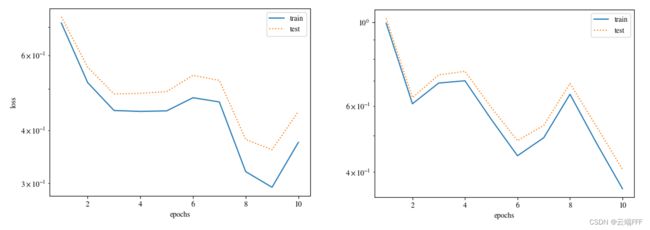
我上面的程序中也可以通过主函数中的train_size参数设置训练使用的样本量,从而控制数据复杂度,但是这里调整的效果不太好,可能是因为 Fashion-MNIST 分类任务太难了,需要很多次训练来取平均
2.2.2 利用 Pytorch 简洁实现
- 在PyTorch中,我们只需要在全连接层后添加
nn.Dropout层并指定丢弃概率即可实现丢弃法 - 训练模型时,Dropout层将以指定的丢弃概率随机丢弃上一层的输出元素;在测试模型时(即
model.eval()后),Dropout层不发挥作用 - 下面给出可以在 vscode 直接运行的完整代码,同时删除了绘图等附加代码
import torch from torch import nn import torchvision import torchvision.transforms as transforms import numpy as np from IPython import display # 数据集相关 -------------------------------------------------------------------------------------------------- # 加载数据集 def load_data_fashion_mnist(batch_size, num_workers=0, root='./Datasets/FashionMNIST'): mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True,transform=transforms.ToTensor()) mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True,transform=transforms.ToTensor()) train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers) test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers) return train_iter, test_iter # 模型定义 -------------------------------------------------------------------------------------------------------- class FlattenLayer(nn.Module): def __init__(self): super(FlattenLayer, self).__init__() def forward(self, x): # x shape: (batch, *, *, ...) return x.view(x.shape[0], -1) # 评估模型(注意不进行 dropout 操作) def evaluate_accuracy(data_iter, net): acc_sum, n = 0.0, 0 for X, y in data_iter: # 使用 pytorch 模型 if isinstance(net, torch.nn.Module): # 评估模式, 这会关闭dropout net.eval() # 累计 batch 中预测对的样本数量 acc_sum += (net(X).argmax(dim=1) == y).float().sum().item() # 改回训练模式 net.train() # 自定义模型 else: # 如果 callable 对象 net 中有 is_training 这个参数 if('is_training' in net.__code__.co_varnames): # func.__code__.co_varnames 将函数局部变量以元组的形式返回。 acc_sum += (net(X, is_training=False).argmax(dim=1) == y).float().sum().item() # 将is_training设置成False else: acc_sum += (net(X).argmax(dim=1) == y).float().sum().item() # 总样本数 n += y.shape[0] return acc_sum / n def train(net, train_iter, test_iter, loss, num_epochs, batch_size, params=None, lr=None, optimizer=None): # 训练执行 num_epochs 轮 for epoch in range(num_epochs): train_l_sum = 0.0 # 本 epoch 总损失 train_acc_sum = 0.0 # 本 epoch 总准确率 n = 0 # 本 epoch 总样本数 # 逐小批次地遍历训练数据 for X, y in train_iter: # 计算小批量损失 y_hat = net(X) l = loss(y_hat, y).sum() # 梯度清零 optimizer.zero_grad() # 小批量的损失对模型参数求梯度 l.backward() # 做小批量随机梯度下降进行优化 optimizer.step() # 记录训练数据 train_l_sum += l.item() train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item() n += y.shape[0] # 训练完成一个 epoch 后,评估测试集上的准确率 test_acc = evaluate_accuracy(test_iter, net) # 打印提示信息 print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f' % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc)) if __name__ == '__main__': # 输入输出维度 num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256 # 超参数 num_epochs, lr = 10, 0.5 # 获取数据读取迭代器 batch_size = 256 train_iter, test_iter = load_data_fashion_mnist(batch_size, 4) # 定义模型网络结构 drop_prob1, drop_prob2 = 0.2, 0.5 net = nn.Sequential( FlattenLayer(), nn.Linear(num_inputs, num_hiddens1), nn.ReLU(), nn.Dropout(drop_prob1), nn.Linear(num_hiddens1, num_hiddens2), nn.ReLU(), nn.Dropout(drop_prob2), nn.Linear(num_hiddens2, 10) ) # 初始化模型参数 W1 = torch.tensor(np.random.normal(0, 0.01, size=(num_inputs, num_hiddens1)), dtype=torch.float, requires_grad=True) b1 = torch.zeros(num_hiddens1, requires_grad=True) W2 = torch.tensor(np.random.normal(0, 0.01, size=(num_hiddens1, num_hiddens2)), dtype=torch.float, requires_grad=True) b2 = torch.zeros(num_hiddens2, requires_grad=True) W3 = torch.tensor(np.random.normal(0, 0.01, size=(num_hiddens2, num_outputs)), dtype=torch.float, requires_grad=True) b3 = torch.zeros(num_outputs, requires_grad=True) params = [W1, b1, W2, b2, W3, b3] # 损失 & 优化器 loss = nn.CrossEntropyLoss() optimizer = torch.optim.SGD(net.parameters(), lr=lr) # 学习率 0.1 # 进行训练 train(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer) ''' epoch 1, loss 0.0035, train acc 0.673, test acc 0.774 epoch 2, loss 0.0021, train acc 0.805, test acc 0.812 epoch 3, loss 0.0018, train acc 0.832, test acc 0.813 epoch 4, loss 0.0017, train acc 0.846, test acc 0.853 epoch 5, loss 0.0016, train acc 0.853, test acc 0.825 epoch 6, loss 0.0015, train acc 0.859, test acc 0.850 epoch 7, loss 0.0014, train acc 0.866, test acc 0.818 epoch 8, loss 0.0014, train acc 0.869, test acc 0.854 epoch 9, loss 0.0014, train acc 0.872, test acc 0.865 epoch 10, loss 0.0013, train acc 0.876, test acc 0.855 '''