PyTorch：train模式与eval模式的那些坑

前言

  博主在最近开发过程中不小心被pytorch中train模式与eval模式坑了一下o(*≧д≦)o!!，被坑的起因就不说了，本篇将详细介绍train模式与eval模式误用对模型带来的影响及BatchNorm的数学原理。

1. train模式与eval模式

  使用过pytorch深度学习框架的小伙伴们肯定知道，通常我们在训练模型前会加上model.train()这行代码，或者干脆不加，而在测试模型前会加上model.test()这行代码。
  先来看看这两个模式是干嘛用的：

    def train(self: T, mode: bool = True) -> T:
        r"""Sets the module in training mode.

        This has any effect only on certain modules. See documentations of
        particular modules for details of their behaviors in training/evaluation
        mode, if they are affected, e.g. :class:`Dropout`, :class:`BatchNorm`,
        etc.

        Args:
            mode (bool): whether to set training mode (``True``) or evaluation
                         mode (``False``). Default: ``True``.

        Returns:
            Module: self
        """
        if not isinstance(mode, bool):
            raise ValueError("training mode is expected to be boolean")
        self.training = mode
        for module in self.children():
            module.train(mode)
        return self

    def eval(self: T) -> T:
        r"""Sets the module in evaluation mode.

        This has any effect only on certain modules. See documentations of
        particular modules for details of their behaviors in training/evaluation
        mode, if they are affected, e.g. :class:`Dropout`, :class:`BatchNorm`,
        etc.

        This is equivalent with :meth:`self.train(False) `.

        See :ref:`locally-disable-grad-doc` for a comparison between
        `.eval()` and several similar mechanisms that may be confused with it.

        Returns:
            Module: self
        """
        return self.train(False)

  根据上述的官方源码，可以得到以下信息：

eval()	将 module 设置为测试模式, 对某些模块会有影响, 比如Dropout和BatchNorm, 与 self.train(False) 等效
train(mode=True)	将 module 设置为训练模式, 对某些模块会有影响, 比如Dropout和BatchNorm

  Dropout和BatchNorm被宠幸的原因如下：

# Dropout
self.dropout = nn.Dropout(p=0.5)

  Dropout层可以通过随即减少神经元的连接，能够把稠密的神经网络变成稀疏的神经网络，这样可以缓解过拟合(神经网络中神经元的连接越多，模型越复杂，模型越容易过拟合)(事实上，Dropout层表现并没有那么好)。

# BatchNorm2d
self.bn = nn.BatchNorm2d(num_features=128)

  BatchNorm层可以对mini-batch数据进行归一化来加速神经网络训练，加速模型的收敛速度及稳定性，除此之外，还可以缓解模型层数过多引入的梯度爆炸问题。

  在训练模型时，将模型的模式设置为train很容易理解，但是我们在测试模型时，我们需要使用所有的神经网络的神经元，这个时候就需要禁止Dropout层发挥作用了，否则的话，模型的精度会有所降低。而测试模式下的BatchNorm层会使用训练时的均值及方差，不再使用测试模型时输入数据的均值及方差(稍后来解释为什么要这样)。

  OK，有了上述的简要介绍，我们来做个小实验，来看一下train模式与eval模式对模型的结果会有多大的影响。默认情况下，构建好模型之后就处于train模式：

from torchvision.models import resnet152


if __name__ == '__main__':
    model = resnet152()
    print(model.training)

# True

  倘若我们在测试模型的时候，没有将模型设置成eval模式下会怎样呢？我从ImageNet数据集中选了20张图片来进行测试模型：

  先看看正常情况下的结果：

import torch
from torchvision.models import resnet152
from torch.nn import functional as F
from torchvision import transforms
from PIL import Image
import pickle
import glob
import pandas as pd


if __name__ == '__main__':
    label_info = pd.read_csv('imagenet2012_label.csv')

    transform = transforms.Compose([
        # transforms.Resize(256),
        # transforms.CenterCrop(224),
        transforms.ToTensor(),
        transforms.Normalize(
            mean=[0.485, 0.456, 0.406],
            std=[0.229, 0.224, 0.225]
        )])

    model = resnet152()
    ckpt = torch.load('pretrained/resnet152-394f9c45.pth')
    model.load_state_dict(ckpt)
    model.eval()
    # model.train()

    file_list = glob.glob('imgs/*.JPEG')
    file_list = sorted(file_list)
    for file in file_list:
        img = Image.open(file)

        img = transform(img)
        img = img.unsqueeze(dim=0)

        output = model(img)
        data_softmax = F.softmax(output, dim=1).squeeze(dim=0).detach().numpy()
        index = data_softmax.argmax()

        results = label_info.loc[index, ['index', 'label', 'zh_label']].array
        print('index: {}, label: {}, zh_label: {}'.format(results[0], results[1], results[2]))

  结果完全正确：

index: 162, label: beagle, zh_label: 狗
index: 101, label: tusker, zh_label: 大象
index: 484, label: catamaran, zh_label: 帆船
index: 638, label: maillot, zh_label: 泳衣
index: 475, label: car_mirror, zh_label: 反光镜
index: 644, label: matchstick, zh_label: 火柴
index: 881, label: upright, zh_label: 钢琴
index: 21, label: kite, zh_label: 鸟
index: 987, label: corn, zh_label: 玉米
index: 141, label: redshank, zh_label: 鸟
index: 335, label: fox_squirrel, zh_label: 松鼠
index: 832, label: stupa, zh_label: 皇宫
index: 834, label: suit, zh_label: 西装
index: 455, label: bottlecap, zh_label: 瓶盖
index: 847, label: tank, zh_label: 坦克
index: 248, label: Eskimo_dog, zh_label: 狗
index: 92, label: bee_eater, zh_label: 鸟
index: 959, label: carbonara, zh_label: 意大利面
index: 884, label: vault, zh_label: 拱廊
index: 0, label: tench, zh_label: 鱼

  接下来将模型设置为train模式，再次进行测试，结果如下：

index: 600, label: hook, zh_label: 钩子
index: 600, label: hook, zh_label: 钩子
index: 600, label: hook, zh_label: 钩子
index: 600, label: hook, zh_label: 钩子
index: 600, label: hook, zh_label: 钩子
index: 600, label: hook, zh_label: 钩子
index: 600, label: hook, zh_label: 钩子
index: 600, label: hook, zh_label: 钩子
index: 463, label: bucket, zh_label: 水桶
index: 600, label: hook, zh_label: 钩子
index: 463, label: bucket, zh_label: 水桶
index: 600, label: hook, zh_label: 钩子
index: 600, label: hook, zh_label: 钩子
index: 600, label: hook, zh_label: 钩子
index: 600, label: hook, zh_label: 钩子
index: 463, label: bucket, zh_label: 水桶
index: 600, label: hook, zh_label: 钩子
index: 600, label: hook, zh_label: 钩子
index: 600, label: hook, zh_label: 钩子
index: 600, label: hook, zh_label: 钩子

  哦豁，发生了什么！这个结果很让人意外啊，模型输出完全错误！
  ResNet152不含有Dropout层，那引起这个结果的原因就只有一个了，那就是BatchNorm层搞的鬼。

2. BatchNorm

  在pytorch中，BatchNorm的定义如下：

torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True, device=None, dtype=None)

# Parameters:
- num_features:	C from an expected input of size (N, C, H, W)
- eps: a value added to the denominator for numerical stability. Default: 1e-5
- momentum: the value used for the running_mean and running_var computation. Can be set to None for cumulative moving average (i.e. simple average). Default: 0.1
- affine: a boolean value that when set to True, this module has learnable affine parameters. Default: True
- track_running_stats: a boolean value that when set to True, this module tracks the running mean and variance, and when set to False, this module does not track such statistics, and initializes statistics buffers running_mean and running_var as None. When these buffers are None, this module always uses batch statistics. in both training and eval modes. Default: True

# Shape:
- Input: (N, C, H, W)
- Output: (N, C, H, W)(same shape as input)

# num_features	表示输入特征的数量，如果输入 tensor 为 (N, C, H, W)， 则 num_features 的值为 C
# eps			表示在分母中添加的一个值，防止出现分母为 0 的情况，默认值为 0.00001
# momentum		在计算 running_mean 和 running_var 时会使用这个参数，默认值为 0.1
# affine		当设置为 True 时，BatchNorm 有可以学习的参数 γ 和 β，默认值为 True
# track_running_stats	当设置为 True 时，BatchNorm 会跟踪数据的均值和方差；当设置为False时，BatchNorm 不会跟踪此类统计信息，并将 running_mean 和 running_var 的统计缓冲区初始化为 None。当这些缓冲区为 None 时，在 train 模式和 eval 模式下 BatchNorm 始终使用批处理统计信息， 默认值为 True

  搭个简单的模型看一下：

import torch
from torch import nn


seed = 10001
torch.manual_seed(seed)


class MyModel(nn.Module):
    def __init__(self):
        super(MyModel, self).__init__()

        self.conv = nn.Conv2d(in_channels=3, out_channels=10, kernel_size=5, stride=1)
        self.bn = nn.BatchNorm2d(num_features=10, eps=1e-5, momentum=0.1, affine=True, track_running_stats=True)
        self.relu = nn.ReLU()
        self.pool = nn.AdaptiveAvgPool2d(output_size=1)
        self.linear = nn.Linear(in_features=10, out_features=1)

    def forward(self, x):
        x = self.conv(x)
        var, mean = torch.var_mean(x, dim=[0, 2, 3])
        print("x's mean: {}\nx's var: {}".format(mean.detach().numpy(), var.detach().numpy()))
        
        x = self.bn(x)
        print('-----------------------------------------------------------------------------------')
        print("x's mean: {}\nx's var: {}".format(self.bn.running_mean.numpy(), self.bn.running_var.numpy()))
        
        x = self.relu(x)
        x = self.pool(x)
        x = x.view(x.size(0), -1)
        output = self.linear(x)

        return output


if __name__ == '__main__':
    model = MyModel()

    inputs = torch.randn(size=(128, 3, 32, 32))
    model(inputs)

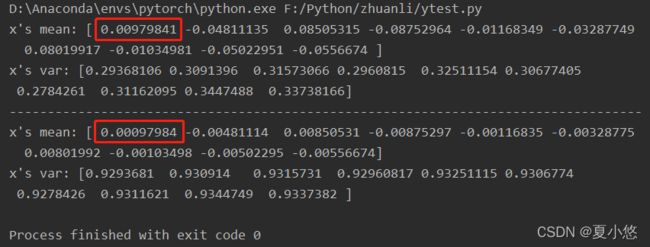
  运行一下上面的模型会发现，我们手动计算卷积后的特征的均值与方差和BatchNorm层计算出来的均值与方差并不一致，但是能发现一些端倪，手动计算的均值与BatchNorm层计算出来的均值相差了10倍，这个不同点就是上述参数momentum造成的，其默认值就是0.1。

  参数momentum的值更改为1.0，再次运行模型，此时的卷积后的特征的均值与方差和BatchNorm层计算出来的均值与方差完全一致：

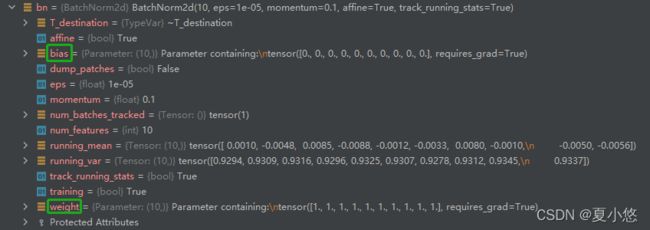
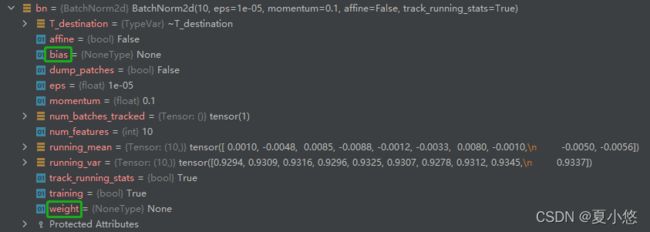
  来看下参数affine在BatchNorm中的具体作用，下图分别是affine=True和affine=False：

  很明显，affine=True时BatchNorm层有了可训练的参数weight和bias。

  最后，再来看一下一个非常重要的参数：track_running_stats
  注意看上面的图中num_batches_tracked的值，当我们将参数track_running_stats的值设置为True，BatchNorm就会统计送入的数据，此时的num_batches_tracked值为1，也就是记录了一个mini-batch的均值running_mean和方差running_var。更改下代码多计算几次：

if __name__ == '__main__':
    model = MyModel()

    inputs = torch.randn(size=(128, 3, 32, 32))
    for i in range(10):
        model(inputs)
    print('num_batches_tracked: ', model.bn.num_batches_tracked.numpy())

# num_batches_tracked:  10

  为了更具有说服力，我们再更改下代码，来对比一下BatchNorm是如何统计数据的：

class MyModel(nn.Module):
    def __init__(self):
        super(MyModel, self).__init__()

        self.conv = nn.Conv2d(in_channels=3, out_channels=10, kernel_size=5, stride=1)
        self.bn = nn.BatchNorm2d(num_features=10, eps=1e-5, momentum=1.0, affine=True, track_running_stats=True)
        self.relu = nn.ReLU()
        self.pool = nn.AdaptiveAvgPool2d(output_size=1)
        self.linear = nn.Linear(in_features=10, out_features=1)

        self.var_data = []
        self.mean_data = []

    def forward(self, x):
        x = self.conv(x)

        var, mean = torch.var_mean(x, dim=[0, 2, 3])
        self.var_data.append(var)
        self.mean_data.append(mean)

        x = self.bn(x)
        x = self.relu(x)
        x = self.pool(x)
        x = x.view(x.size(0), -1)
        output = self.linear(x)

        return output


if __name__ == '__main__':
    model = MyModel()

    for i in range(10):
        inputs = torch.randn(size=(128, 3, 32, 32))
        model(inputs)

    var = model.var_data[-1]
    mean = model.mean_data[-1]
    print("x's mean: {}\nx's var: {}".format(mean.detach().numpy(), var.detach().numpy()))
    print('-----------------------------------------------------------------------------------')
    print("x's mean: {}\nx's var: {}".format(model.bn.running_mean.numpy(), model.bn.running_var.numpy()))

  与我当初想的不太一样，我以为是历史以往所有的样本的均值与方差，其实并不是，根据实际的结果来看，BatchNorm记录的均值与方差始终是最后一个mini-batch样本的均值与方差，即只将当前的数据进行归一化。

3. 数学原理

  BatchNorm算法出自Google的一篇论文：Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift。

  根据论文中的公式，可以得到BatchNorm算法的表达式$$\mathbf{y}=\gamma \cdot \frac{\mathbf{x}-E(\mathbf{x})}{\sqrt{Var(\mathbf{x})+ϵ}}+\beta$$  其中，$\mathbf{x}$是输入张量的值，$ϵ$是一个较小的浮点数，以防止分母为0。
  以BatchNorm2d为例，平均值和方差都是相对于N、H、W三个方向进行计算和平均的，具体如下：
$$E({\mathbf{x}}_c)=\frac{1}{N\times H\times W}\sum _{N,H,W}{\mathbf{x}}_c$$$$Var({\mathbf{x}}_c)=\frac{1}{N\times H\times W}\sum _{N,H,W}({\mathbf{x}}_c-E({\mathbf{x}}_c){)}^2$$  根据计算公式可以知道，统计量的输出是一个大小为C的向量。

  由于在求统计量的过程中包含了mini-batch N的平均，所以BatchNorm又称为批次归一化方法，只改变输入tensor的数据分布，不改变tensor的形状。

  接下来再跟着公式来看下pytorch中的BatchNorm2d的参数：
  参数momentum控制着指数移动平均计算$E(\mathbf{x})$和$Var(\mathbf{x})$时的动量, 计算公式如下：
$${\hat{x}}_{new}=(1-\alpha )\hat{x}+\alpha {\hat{x}}_t$$  其中$\alpha$是动量的值，${\hat{x}}_t$是当前的$E(\mathbf{x})$或$Var(\mathbf{x})$的计算值，$\hat{x}$是上一步的指数移动平均的估计值，${\hat{x}}_{new}$是当前的指数移动平均的估计值。
  参数affine决定了是否在归一化后做仿射变换，即是否设定$\beta$和$\gamma$参数，affine=True表示$\beta$和$\gamma$是可训练的标量参数，affine=False表示$\beta$和$\gamma$是固定的标量参数，即$\beta =0$，$\gamma =1$。
  参数track_running_stats决定了是否使用指数移动平均来估计当前的统计参量，默认是使用的，如果设置track_running_stats=False，则直接使用当前统计量的计算值${\hat{x}}_t$来对$E(\mathbf{x})$和$Var(\mathbf{x})$进行估计。

  仿射变换 = 线性变换 + 平移

结束语

  在实际应用中，通常会将mini-batch设置稍微大些，比如128, 256，如果设置的太小，可能会导致数据变化很剧烈，模型很难收敛，毕竟mini-batch只是数据集中的很小一部分数据。