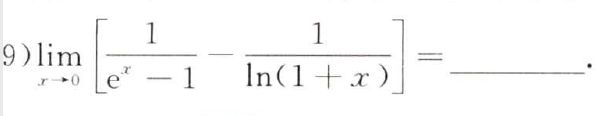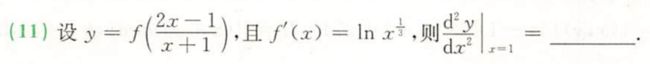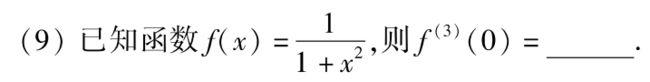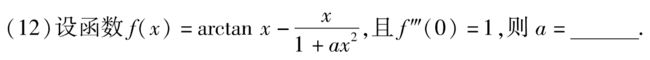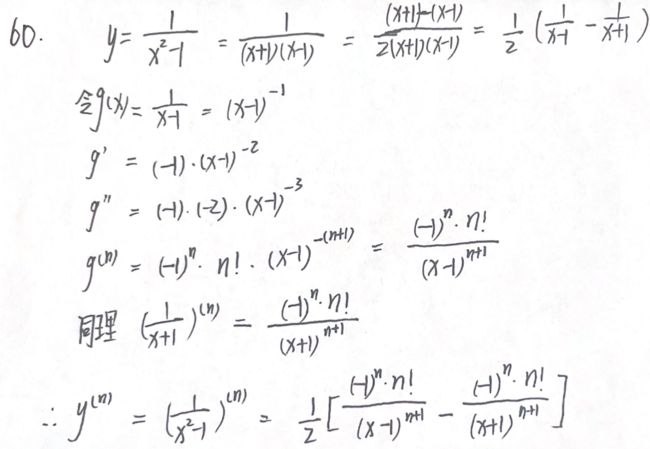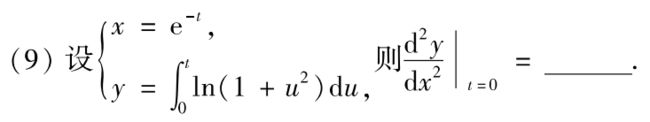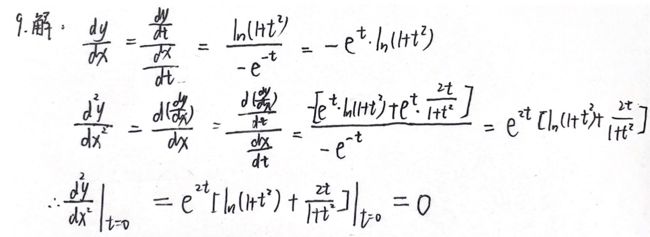高等数学(上) —— 一元微分学
文章目录
- Ch1.极限
-
- 函数 (函数四性态)
-
- 单调性
- 奇偶性
- 对称性
- 周期性
- 数列极限与函数极限
-
- 数列极限
- 函数极限
-
- 函数极限的保号性
- 等价无穷小
- 两个重要极限
- 求极限(求极限的方法)
- 证明极限存在:极限存在准则/极限存在定理 (2个)
-
- 单调有界准则
- 夹逼定理
- 连续
-
- 连续性与间断点
-
- 间断点的定义
- 间断点的分类
- 连续与可导
- 连续与极限
- Ch2.导数
-
- 2.1 导数概念
-
- 导数定义
- 导数的几何意义
- 2.2 函数的求导法则
-
- 导数公式
- 复合函数的链式求导法则
- 2.3 高阶导数
-
- 求n阶导数的三种方法 (武老师)
- 2.4 隐函数及参数方程的导数
-
- 隐函数的导数
- 由参数方程所确定的函数的导数
- 含绝对值的导数
- 2.5 一元可微
- Ch3.中值定理
-
- 费马引理
- 罗尔定理
- 拉格朗日中值定理
- 柯西中值定理
- 洛必达法则
- 泰勒公式
-
- 泰勒中值定理1:
- 泰勒中值定理2:
- 麦克劳林公式
- 极值与拐点
-
- 极值
- 拐点
- 渐近线
-
- 铅直渐近线
- 水平渐近线
- 斜渐近线
- 曲率、曲率半径
- Ch4.不定积分
- Ch5.定积分
- Ch6.定积分应用
- Ch7.微分方程
Ch1.极限
函数 (函数四性态)
单调性
1. f ( x ) 单增⇦⇨ f ′ ( x ) ≥ 0 f(x)单增 ⇦⇨ f'(x)≥0 f(x)单增⇦⇨f′(x)≥0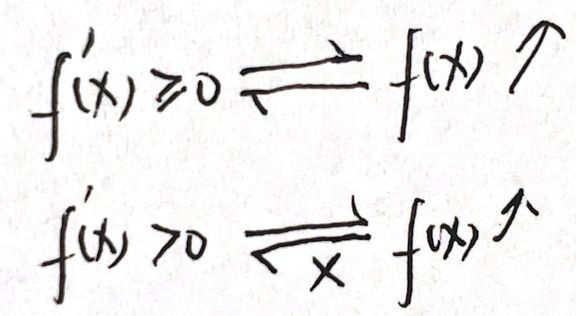
2.f每多一个负号,单调性发生变化:f(x)单增,则f(-x)单减,-f(-x)单增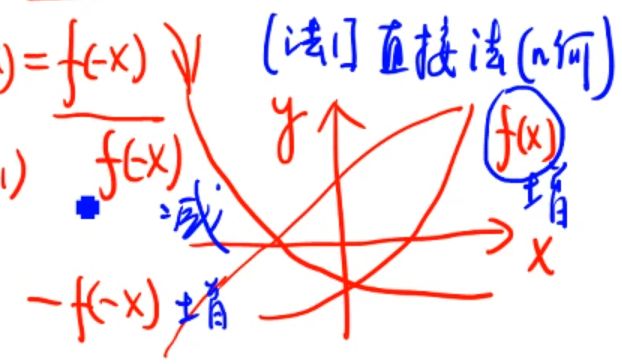
例题1:武钟祥老师每日一题 24.Day62 单调性

答案:D
奇偶性
1.奇函数: f ( − x ) = − f ( x ) f(-x)=-f(x) f(−x)=−f(x)
若奇函数在x=0处有定义,则 f 奇 ( 0 ) = 0 f_{奇}(0)=0 f奇(0)=0(奇函数的必要条件)
3. f ( ∣ x ∣ ) 与 ∣ f ( x ) ∣ f(|x|)与|f(x)| f(∣x∣)与∣f(x)∣: ∣ y ∣ |y| ∣y∣是关于y的偶函数
例题1:07年3. f ( x ) f(x) f(x)为奇函数,则 F ( x ) F(x) F(x)为偶函数

答案:C
例题2:19年12. ∣ y ∣ |y| ∣y∣是关于y的偶函数
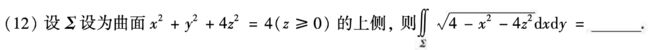
答案: 32 3 \dfrac{32}{3} 332
对称性
1. f ( x ) f(x) f(x)与 f ( − x ) f(-x) f(−x)关于 y 轴对称 y轴对称 y轴对称
2. f ( x ) f(x) f(x)与 − f ( x ) -f(x) −f(x)关于 x 轴对称 x轴对称 x轴对称
例题1:注意函数的对称性。2023年19.曲面积分就是对称性。
周期性
y ( x ) = y ( x + T ) y(x)=y(x+T) y(x)=y(x+T)
例题1:18年18(2)
数列极限与函数极限
数列极限
例题1:19年18. 数列极限:定积分的保号性、三角换元(有根式)、夹逼定理

分析:
f(x)单调 + {xn}单调 = {f(xn)}单调
f(x)单调 + f{xn}单调 = {xn}单调
对于CD,举个反例:f(x)=arctanx单调有界,{xn}=n(n=1,2,3,…),则 { f ( x n ) } = arctan n \{f(x_n)\}=\arctan n {f(xn)}=arctann,收敛于 π 2 \dfrac{π}{2} 2π,而 lim n → ∞ { x n } = lim n → ∞ n = ∞ \lim\limits_{n→∞}\{x_n\}=\lim\limits_{n→∞}n=∞ n→∞lim{xn}=n→∞limn=∞,{xn}发散
答案:B
函数极限
函数极限的保号性
如果 lim x → x 0 f ( x ) = A ,且 A > 0 , \lim\limits_{x→x_0}f(x)=A,且A>0, x→x0limf(x)=A,且A>0,那么存在常数 δ > 0 δ>0 δ>0,使得当 0 < ∣ x − x 0 ∣ < δ 0<|x-x_0|<δ 0<∣x−x0∣<δ 时,有 f ( x ) > 0 f(x)>0 f(x)>0(同理 A < 0 A<0 A<0 时,有 f ( x ) < 0 f(x)<0 f(x)<0)
例题2:武忠祥老师每日一题 24.Day65 保号性、极值

分析:
答案:B
等价无穷小
a x − 1 ∼ x ln x a^x-1\sim x\ln x ax−1∼xlnx
同阶无穷小 ⇦⇨ 阶数相同 ⇦⇨ 相除,趋于0时的极限=k(k为非零的任意常数)
等价无穷小 ⇦⇨ 阶数相同,系数也相同 ⇦⇨ 相除,趋于0时的极限=1
阶 = (里面被积的阶+1)×外面上限的阶
( 1 + x ) μ ∼ μ x (1+x)^μ\sim μx (1+x)μ∼μx
例如: 1 + x ∼ x 2 \sqrt{1+x}\sim \dfrac{x}{2} 1+x∼2x
例题1:07年1. 等价无穷小 ⇦⇨ 阶数相同,系数也相同 ⇦⇨ 相除,趋于0时的极限=1
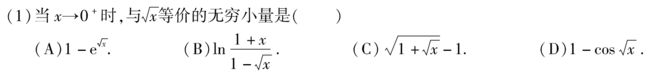
分析:
C: 1 + x − 1 ∼ x 2 \sqrt{1+\sqrt{x}}-1\sim \dfrac{\sqrt{x}}{2} 1+x−1∼2x
B: lim x → 0 + ln 1 + x 1 − x x = lim x → 0 + ln ( 1 + x + x 1 − x ) x = lim x → 0 + x + x 1 − x x = lim x → 0 + 1 + x 1 − x = 1 \lim\limits_{x→0^+}\dfrac{\ln\dfrac{1+x}{1-\sqrt{x}}}{\sqrt{x}}=\lim\limits_{x→0^+}\dfrac{\ln(1+\dfrac{x+\sqrt{x}}{1-\sqrt{x}})}{\sqrt{x}}=\lim\limits_{x→0^+}\dfrac{\dfrac{x+\sqrt{x}}{1-\sqrt{x}}}{\sqrt{x}}=\lim\limits_{x→0^+}\dfrac{1+\sqrt{x}}{1-\sqrt{x}}=1 x→0+limxln1−x1+x=x→0+limxln(1+1−xx+x)=x→0+limx1−xx+x=x→0+lim1−x1+x=1
答案:B
分析:阶 = (里面被积的阶+1)×外面上限的阶
A: ∫ 0 x ( e t 2 − 1 ) d t ∼ \int_0^x(e^{t^2}-1){\rm d}t\sim ∫0x(et2−1)dt∼ ∫ 0 x t 2 d t \int_0^xt^2{\rm d}t ∫0xt2dt,阶=2+1=3
B: ∫ 0 x l n \int_0^x\rm ln ∫0xln ( 1 + t 3 ) d t ∼ ∫ 0 x t 3 d t = ∫ 0 x t 3 2 d t (1+\sqrt{t^3}){\rm d}t\sim\int_0^x\sqrt{t^3}{\rm d}t=\int_0^xt^{\frac{3}{2}}{\rm d}t (1+t3)dt∼∫0xt3dt=∫0xt23dt,阶=1.5+1=2.5
C: ∫ 0 s i n x sin t 2 d t ∼ ∫ 0 s i n x t 2 d t \int_0^{sinx}\sin t^2{\rm d}t\sim \int_0^{sinx}t^2dt ∫0sinxsint2dt∼∫0sinxt2dt,阶=2+1=3
D: ∫ 0 1 − c o s x s i n 3 t d t ∼ \int_0^{1-cosx}\rm \sqrt{sin^3t}dt\sim ∫01−cosxsin3tdt∼ ∫ 0 1 2 x 2 t 3 2 d t \int_0^{\frac{1}{2}x^2}t^{\frac{3}{2}}dt ∫021x2t23dt,阶=(1.5+1)×2=5
答案:D
两个重要极限
lim x → 0 sin x x = 1 lim x → ∞ ( 1 + 1 x ) x = lim x → 0 ( 1 + x ) 1 x = e \lim\limits_{x→0}\dfrac{\sin x}{x}=1\\[8mm] \lim\limits_{x→∞}(1+\dfrac{1}{x})^x=\lim\limits_{x→0}(1+x)^\frac{1}{x}=e x→0limxsinx=1x→∞lim(1+x1)x=x→0lim(1+x)x1=e
答案:
例题2:06年16. (1)证明极限存在——单调有界准则:单调有界必有极限 (2)凑重要极限,求极限
分析:
(1)证明极限存在——单调有界准则:单调有界必有极限
(2)凑重要极限,求极限

答案: e − 1 6 e^{-\frac{1}{6}} e−61
求极限(求极限的方法)
求极限的方法:
①等价无穷小
②洛必达
③泰勒公式
④两个重要极限
⑤有界量×无穷小=无穷小
⑥夹逼准则
⑦导数定义
⑧定积分定义、二重积分定义
例题:20年9. 求极限:洛必达、泰勒公式
分析:
先通分:原式= lim x → 0 [ l n ( 1 + x ) − ( e x − 1 ) ( e x − 1 ) [ l n ( 1 + x ) ] ] = lim x → 0 l n ( 1 + x ) − ( e x − 1 ) x 2 \lim\limits_{x→0}[\dfrac{ln(1+x)-(e^x-1)}{(e^x-1)[ln(1+x)]}]=\lim\limits_{x→0}\dfrac{ln(1+x)-(e^x-1)}{x^2} x→0lim[(ex−1)[ln(1+x)]ln(1+x)−(ex−1)]=x→0limx2ln(1+x)−(ex−1)
方法1:洛必达,一直洛
方法1.5:洛必达法则+提出分子中的分式(提出 1 1 + x \frac{1}{1+x} 1+x1)
lim x → 0 l n ( 1 + x ) − ( e x − 1 ) x 2 = lim x → 0 1 1 + x − e x 2 x \lim\limits_{x→0}\dfrac{ln(1+x)-(e^x-1)}{x^2}=\lim\limits_{x→0}\dfrac{\frac{1}{1+x}-e^x}{2x} x→0limx2ln(1+x)−(ex−1)=x→0lim2x1+x1−ex
(提出 1 1 + x \frac{1}{1+x} 1+x1) = 1 2 lim x → 0 1 1 + x ⋅ 1 − e x ( 1 + x ) x = 1 2 lim x → 0 1 − e x − x e x x = − 1 2 lim x → 0 e x ( x + 1 ) − 1 x = − 1 2 lim x → 0 [ e x ( x + 1 ) + e x ] = − 1 2 lim x → 0 e x ( x + 2 ) = − 1 =\dfrac{1}{2}\lim\limits_{x→0}\dfrac{1}{1+x}·\dfrac{1-e^x(1+x)}{x}=\dfrac{1}{2}\lim\limits_{x→0}\dfrac{1-e^x-xe^x}{x}=-\dfrac{1}{2}\lim\limits_{x→0}\dfrac{e^x(x+1)-1}{x}=-\dfrac{1}{2}\lim\limits_{x→0}[e^x(x+1)+e^x]=-\dfrac{1}{2}\lim\limits_{x→0}e^x(x+2)=-1 =21x→0lim1+x1⋅x1−ex(1+x)=21x→0limx1−ex−xex=−21x→0limxex(x+1)−1=−21x→0lim[ex(x+1)+ex]=−21x→0limex(x+2)=−1
方法2:泰勒公式
l n ( 1 + x ) = x − x 2 2 + o ( x 2 ) ln(1+x)=x-\dfrac{x^2}{2}+o(x^2) ln(1+x)=x−2x2+o(x2)
e x = 1 + x + x 2 2 ! + o ( x 2 ) e^x=1+x+\dfrac{x^2}{2!}+o(x^2) ex=1+x+2!x2+o(x2) ∴ e x − 1 = x + x 2 2 ! + o ( x 2 ) ∴e^x-1=x+\dfrac{x^2}{2!}+o(x^2) ∴ex−1=x+2!x2+o(x2)
lim x → 0 l n ( 1 + x ) − ( e x − 1 ) x 2 = lim x → 0 [ x − x 2 2 + o ( x 2 ) ] − [ x + x 2 2 ! + o ( x 2 ) ] x 2 = lim x → 0 − x 2 + o ( x 2 ) x 2 = − 1 \lim\limits_{x→0}\dfrac{ln(1+x)-(e^x-1)}{x^2}=\lim\limits_{x→0}\dfrac{[x-\frac{x^2}{2}+o(x^2)]-[x+\frac{x^2}{2!}+o(x^2)]}{x^2}=\lim\limits_{x→0}\dfrac{-x^2+o(x^2)}{x^2}=-1 x→0limx2ln(1+x)−(ex−1)=x→0limx2[x−2x2+o(x2)]−[x+2!x2+o(x2)]=x→0limx2−x2+o(x2)=−1
答案:-1
证明极限存在:极限存在准则/极限存在定理 (2个)
单调有界准则
单调有界准则:单调有界,必有极限(数列收敛)
①单调增加,有上界 ②单调减少,有下界
喻老三:考研中证明极限存在,至今为止,每次都考 单调有界准则
收敛和有极限是等价的意思。不过一般只有 数列和级数 才说收敛。
例题2:06年16.
例题3:08年4.
夹逼定理
A 若题目中出现了形如 A 分析:从题目已知,通过变形得到题目所求的夹逼。看到有不等式,可以留意一下是否 变形后能夹逼。 答案:D 例题2:19年18. 1.第一类间断点:左右极限都存在 ①可去间断点:左右极限都存在,且相等 ②跳跃间断点:左右极限都存在,但不等 2.第二类间断点:左右极限至少有一个不存在,为∞ ②振荡间断点:振荡不存在,但是有界,并不是无穷。典型例子sin∞: lim x → 0 sin 1 x \lim\limits_{x→0}\sin\dfrac{1}{x} x→0limsinx1 连续:左极限 = 函数值 =右极限 分析:AB是连续,CD是可导 A: lim x → 0 f ( x ) x 存在 ⇨ lim x → 0 f ( x ) = 0 → 连续 f ( 0 ) = 0 \lim\limits_{x→0}\dfrac{f(x)}{x}存在\ ⇨\ \lim\limits_{x→0}f(x)=0 \xrightarrow{连续}\ f(0)=0 x→0limxf(x)存在 ⇨ x→0limf(x)=0连续 f(0)=0 或者 lim x → 0 f ( x ) = lim x → 0 f ( x ) x ⋅ x = lim x → 0 f ( x ) x ⋅ lim x → 0 x = 0 \lim\limits_{x→0}f(x)=\lim\limits_{x→0}\dfrac{f(x)}{x}·x=\lim\limits_{x→0}\dfrac{f(x)}{x}·\lim\limits_{x→0}x=0 x→0limf(x)=x→0limxf(x)⋅x=x→0limxf(x)⋅x→0limx=0(有界×无穷小 = 无穷小) B:两种方法同理可证 2f(0)=0 C:导数定义 lim x → 0 f ( x ) x = lim x → 0 f ( x ) − f ( 0 ) x − 0 = f ′ ( 0 ) 存在 \lim\limits_{x→0}\dfrac{f(x)}{x}=\lim\limits_{x→0}\dfrac{f(x)-f(0)}{x-0}=f'(0)存在 x→0limxf(x)=x→0limx−0f(x)−f(0)=f′(0)存在 D:举反例,|x|在x=0处不可导 答案:D 例题2:16年4. 若f连续,则 lim n → ∞ f ( x n ) = f ( lim n → ∞ x n ) \lim\limits_{n→∞}f(x_n)=f(\lim\limits_{n→∞}x_n) n→∞limf(xn)=f(n→∞limxn) 1.变化率的极限存在 2. Δ x = h Δx=h Δx=h 3. Δ x = x − x 0 ⇨ x = x 0 + Δ x Δx=x-x_0 ⇨ x=x_0+Δx Δx=x−x0⇨x=x0+Δx 常用结论: 分析:ABC左右导数均相等,为0 答案:D 分析: A、B:题干只说f(x)在(-1,1)内有定义,没说连续,故不可导。取可去间断点的分段函数为反例。A、B❌ C: f(x)在x=0处可导 ⇦⇨ f ′ ( 0 ) = lim x → 0 f ( x ) − f ( 0 ) x − 0 = lim x → 0 f ( x ) x f'(0)=\lim\limits_{x→0}\dfrac{f(x)-f(0)}{x-0}=\lim\limits_{x→0}\dfrac{f(x)}{x} f′(0)=x→0limx−0f(x)−f(0)=x→0limxf(x)存在 ∴f(x)为x的同阶或高阶无穷小 D:当f(x)比x²低阶, f ( x ) x 2 \dfrac{f(x)}{x²} x2f(x)应该为∞,不为0;当f(x)与x²同阶, f ( x ) x 2 \dfrac{f(x)}{x²} x2f(x)应该为 k ≠ 0 k≠0 k=0;举反例,取f(x)=x。D❌ 答案:C 例题3:23李林六套卷(六)12. 参数方程 + 导数定义 答案:4 分析:跳转 答案:D ( tan x ) ′ = sec 2 x (\tan x)'=\sec ^2x (tanx)′=sec2x d y d x = d y d u ⋅ d u d x \dfrac{dy}{dx}=\dfrac{dy}{du}·\dfrac{du}{dx} dxdy=dudy⋅dxdu 分析: 1.公式(n阶导数公式) 2.求1阶、2阶,归纳规律 3.泰勒公式 1.直接求导:无脑求三阶导,然后代值 2.f=uv,莱布尼茨公式: f ( n ) = ( u v ) ( n ) = ∑ k = 0 n C n k u ( n − k ) v k f^{(n)}=(uv)^{(n)}=\sum\limits_{k=0}^n{\rm C}_n^ku^{(n-k)}v^k f(n)=(uv)(n)=k=0∑nCnku(n−k)vk 3.n阶导数公式 4.泰勒公式的唯一性: ∴ f ( n ) ( x 0 ) = a n ⋅ n ! ∴f^{(n)}(x₀)=a_n·n! ∴f(n)(x0)=an⋅n! 即 a 3 = f ( 3 ) ( 0 ) 3 ! = f ′ ′ ′ ( 0 ) 6 a₃=\dfrac{f^{(3)}(0)}{3!}=\dfrac{f'''(0)}{6} \qquad a3=3!f(3)(0)=6f′′′(0) f ′ ′ ′ ( 0 ) = 6 a 3 f'''(0)=6a₃ f′′′(0)=6a3 5.导函数的奇偶性: 分析:方法4:导函数的奇偶性 答案:0 答案: 1 2 \dfrac{1}{2} 21 例题3:武钟祥每日一题 24-Day60 啊,我“拆”开了! 分析: 答案:A 答案:0 分析:“动静”结合:只有趋向于无穷的n是动的,其他变量(如x)都是静的,看作常数 答案:C Δy是(函数的)增量,dy是(函数的)微分 分析: 答案:A 罗尔定理:如果函数f(x)满足: 例题1:13年18. 有两问的问题,考虑把第一问的结果用到第二问上 答案: 若函数f(x)满足: 例题1:16年19. 有两问的问题,考虑把第一问的结果用到第二问上 分子分母同时求导。 例题:20年9. f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + f ′ ′ ′ ( x 0 ) 3 ! ( x − x 0 ) 3 + . . . + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + o ( ( x − x 0 ) n ) f(x)=f(x_0)+f'(x_0)(x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+\dfrac{f'''(x_0)}{3!}(x-x_0)^3+...+\dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n+o((x-x_0)^n) f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+3!f′′′(x0)(x−x0)3+...+n!f(n)(x0)(x−x0)n+o((x−x0)n) 佩亚诺余项(用于计算极限): R n ( x ) = o ( ( x − x 0 ) n ) R_n(x)=o((x-x_0)^n) Rn(x)=o((x−x0)n) f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + f ′ ′ ′ ( x 0 ) 3 ! ( x − x 0 ) 3 + . . . + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + R n ( x ) f(x)=f(x_0)+f'(x_0)(x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+\dfrac{f'''(x_0)}{3!}(x-x_0)^3+...+\dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x) f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+3!f′′′(x0)(x−x0)3+...+n!f(n)(x0)(x−x0)n+Rn(x) 拉格朗日余项(用于证明): R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 ( x 0 < ξ < x ) R_n(x)=\dfrac{f^{(n+1)}(ξ)}{(n+1)!}(x-x_0)^{n+1} (x_0<ξ 例题1:13年1. 分析: arctan x = x − x 3 3 + o ( x 3 ) \arctan x=x-\dfrac{x^3}{3}+o(x^3) arctanx=x−3x3+o(x3) 例题2:16年12. 用泰勒公式求高阶导数 f ′ ′ ′ ( 0 ) f'''(0) f′′′(0) 答案: 1 2 \dfrac{1}{2} 21 例题3:20年9. 1.极值的定义: 2.极值的必要条件: 3.极值第一充分条件 4.极值第二充分条件 分析:极值点是驻点 ( f ′ ( x 0 ) = 0 ) (f'(x₀)=0) (f′(x0)=0)或者不可导点 ( f ′ ( x 0 ) 不存在 ) (f'(x₀)不存在) (f′(x0)不存在) 从左到右依次为:驻点a,驻点b,不可导点0,驻点c 答案:C 例题2:武24 D67 极值第二充分条件: f ′ ′ ( x ) > 0 ,极小值 f''(x)>0,极小值 f′′(x)>0,极小值 答案:B 0.凹凸性 凸:① f ( x 1 + x 2 2 ) > f ( x 1 ) + f ( x 2 ) 2 f(\dfrac{x_1+x_2}{2})>\dfrac{f(x_1)+f(x_2)}{2} f(2x1+x2)>2f(x1)+f(x2) ② f ′ ′ ( x ) < 0 f''(x)<0 f′′(x)<0 1.拐点的定义:连续曲线的凹弧与凸弧的分界点。即经过该点 ( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0,f(x0)),曲线的凹凸性改变了,则该点为拐点。(形象点说,拐点就是曲线增长率由加速变到减速,或由减速变到加速的点。二阶导可以理解为加速度,加速度a变号的点,就是拐点) 2.拐点的必要条件: f ′ ′ ( x 0 ) = 0 f''(x_0)=0 f′′(x0)=0 或 f ′ ′ ( x 0 ) f''(x_0) f′′(x0)不存在 3.拐点的充分条件: 4.极值点 vs 拐点: 5.一个点不可能同时为极值点和拐点:若为极值点,则不会是拐点。若为拐点,则不会是极值点。 奇数阶导数不为0:拐点 ;举例: f ′ ( x 0 ) = f ′ ′ ( x 0 ) = f ′ ′ ′ ( x 0 ) = f ( 4 ) ( x 0 ) = 0 , f ( 5 ) ( x 0 ) ≠ 0 f'(x_0)=f''(x_0)=f'''(x_0)=f^{(4)}(x_0)=0,f^{(5)}(x_0)≠0 f′(x0)=f′′(x0)=f′′′(x0)=f(4)(x0)=0,f(5)(x0)=0,则 x 0 x_0 x0为拐点 分析: 答案:C 分析:① 穿针引线法:右上穿入,奇过偶不过 显然2和4是极值点,不是拐点。排除BD 答案:C 例题3:武忠祥老师每日一题 24.Day66. 拐点是一个二维坐标 化简可得 y ′ ′ = 10 9 x − 4 3 ( x + 1 ) y''=\dfrac{10}{9}x^{-\frac{4}{3}}(x+1) y′′=910x−34(x+1) 充分条件2:f’‘(x)在 x 0 x_0 x0两侧变号,可见y’'在-1左右变号,在0左右不变号。则(-1,-6)是拐点 答案: ( − 1 , − 6 ) (-1,-6) (−1,−6) 分析顺序:①铅直渐渐线(找无穷间断点)→ ②水平渐近线(双向)→ ③斜渐近线(双向) 铅直渐近线可以有无数条,而 水平渐近线+斜渐近线 最多只能有2条,为x轴的正向和负向 有无穷间断点a,则 x=a 为曲线的铅直渐近线 水平渐近线有+∞和-∞两个方向 若有 lim x → + ∞ f ( x ) = c \lim\limits_{x→+∞}f(x)=c x→+∞limf(x)=c 或者 lim x → − ∞ f ( x ) = c \lim\limits_{x→-∞}f(x)=c x→−∞limf(x)=c 斜渐近线也有+∞和-∞两个方向。有该方向上的水平渐近线,则无该方向上的斜渐近线。即,水平渐近线 + 斜渐近线 ≤ 2 若有 lim x → + ∞ f ( x ) x = a ≠ 0 \lim\limits_{x→+∞}\dfrac{f(x)}{x}=a≠0 x→+∞limxf(x)=a=0 且 lim x → + ∞ f ( x ) − a x = b \lim\limits_{x→+∞}f(x)-ax=b x→+∞limf(x)−ax=b 分析:分析顺序:铅直渐渐线→水平渐近线→斜渐近线 答案:D 分析: y = s i n 1 x y=sin\dfrac{1}{x} y=sinx1图像 答案:C 答案: y = 3 x + 2 3 y=\sqrt{3}x+\dfrac{2}{3} y=3x+32 曲率半径 ρ = 1 K ρ=\dfrac{1}{K} ρ=K1 曲率 K = ∣ y ′ ′ ∣ ( 1 + y ′ 2 ) 3 2 K=\dfrac{|y''|}{(1+y'^2)^{\frac{3}{2}}} K=(1+y′2)23∣y′′∣ 答案:C 跳转链接:https://blog.csdn.net/Edward1027/article/details/128503192 跳转此处:https://blog.csdn.net/Edward1027/article/details/127150223

连续
连续性与间断点
间断点的定义
间断点的分类
①无穷间断点:存在无界点 / 瑕点,y(a)=∞,则a为无穷间断点,例如 tan π 2 \tan \dfrac{π}{2} tan2π

连续与可导
可导:左导数 = 右导数
连续与极限
Ch2.导数
2.1 导数概念
导数定义
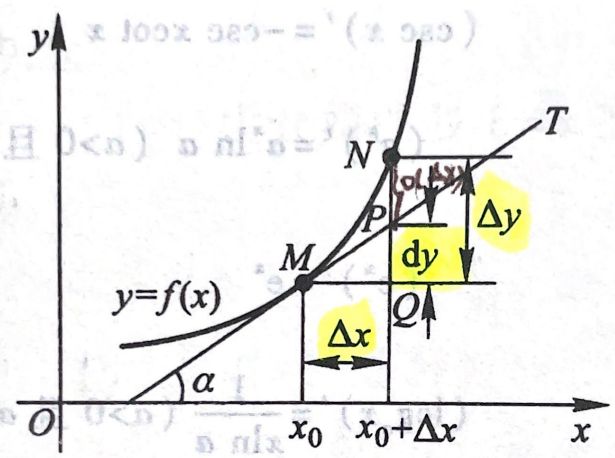
f ′ ( x 0 ) = lim Δ x → 0 Δ y Δ x = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x_0)=\lim\limits_{Δx→0}\frac{Δy}{Δx}=\lim\limits_{Δx→0}\frac{f(x_0+Δx)-f(x_0)}{Δx} f′(x0)=Δx→0limΔxΔy=Δx→0limΔxf(x0+Δx)−f(x0)
f ′ ( x 0 ) = lim h → 0 f ( x 0 + h ) − f ( x 0 ) h f'(x_0)=\lim\limits_{h→0}\frac{f(x_0+h)-f(x_0)}{h} f′(x0)=h→0limhf(x0+h)−f(x0)
f ′ ( x 0 ) = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 f'(x_0)=\lim\limits_{x→x_0}\frac{f(x)-f(x_0)}{x-x_0} f′(x0)=x→x0limx−x0f(x)−f(x0)
f(x)在x=0处可导 ⇦⇨ lim x → 0 f ( x ) − f ( 0 ) x − 0 \lim\limits_{x→0}\dfrac{f(x)-f(0)}{x-0} x→0limx−0f(x)−f(0)存在 ⇦⇨ 左导数=右导数
D的 左导数 f ′ ( 0 − ) = 1 2 ,右导数 f ′ ( 0 + ) = − 1 2 左导数f'(0^-)=\dfrac{1}{2},右导数f'(0^+)=-\dfrac{1}{2} 左导数f′(0−)=21,右导数f′(0+)=−21。左右导数不等,不可导。
又因为 ∣ x ∣ \sqrt{|x|} ∣x∣比x低阶 ∴ lim x → 0 f ( x ) ∣ x ∣ = 0 \lim\limits_{x→0}\dfrac{f(x)}{\sqrt{|x|}}=0 x→0lim∣x∣f(x)=0。 C✔
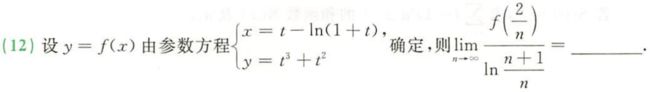
分析:

导数的几何意义
2.2 函数的求导法则
导数公式
( sec x ) ′ = sec x tan x (\sec x)'=\sec x\tan x (secx)′=secxtanx复合函数的链式求导法则
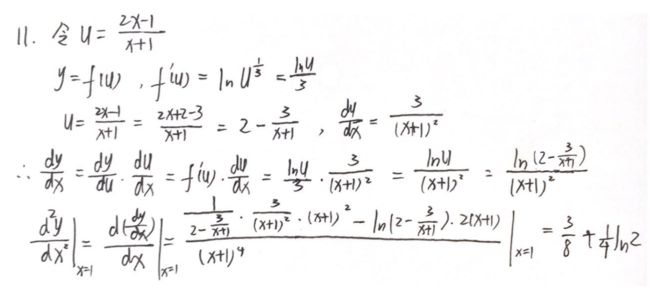
答案: 3 8 + 1 4 ln 2 \dfrac{3}{8}+\dfrac{1}{4}\ln2 83+41ln2
2.3 高阶导数
求n阶导数的三种方法 (武老师)
优点:思路简单,暴力无脑
缺点:计算量大,容易出错
( 1 1 + x ) ( n ) = ( − 1 ) n n ! ( 1 + x ) n + 1 (\dfrac{1}{1+x})^{(n)}=(-1)^n\dfrac{n!}{(1+x)^{n+1}} (1+x1)(n)=(−1)n(1+x)n+1n!
设函数f(x)在x=x₀处具有n阶导数,且
f ( x ) = a 0 + a 1 ( x − x 0 ) + a 2 ( ( x − x 0 ) 2 + a 3 ( x − x 0 ) 3 + . . . + a n ( x − x 0 ) n + o ( ( x − x 0 ) n ) ( x → x 0 ) f(x)=a₀+a₁(x-x₀)+a₂((x-x₀)²+a₃(x-x₀)³+...+a_n(x-x₀)^n+o((x-x₀)^n) (x→x₀) f(x)=a0+a1(x−x0)+a2((x−x0)2+a3(x−x0)3+...+an(x−x0)n+o((x−x0)n)(x→x0)
则一定有 a 0 = f ( x 0 ) , a k = f ( k ) ( x 0 ) k ! , k = 1 , 2 , . . . a₀=f(x₀),a_k=\dfrac{f^{(k)}(x₀)}{k!},k=1,2,... a0=f(x0),ak=k!f(k)(x0),k=1,2,...
f(x)为可导的奇函数,则其导函数为偶函数;f(x)为可导的偶函数,则其导函数为奇函数
f(x)是偶函数,则f’‘’(x)为奇函数,则f’‘’(0)=0
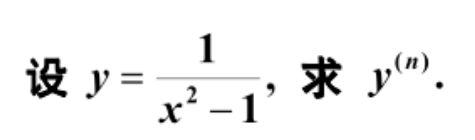
法一(回代法): 求 f ′ ′ ( x ) = 2 f ( x ) f ′ ( x ) ,将 f ′ ( x ) = f 2 ( x ) 代入,得 f ′ ′ ( x ) = 2 f 3 ( x ) 求f''(x)=2f(x)f'(x),将f'(x)=f²(x)代入,得f''(x)=2f³(x) 求f′′(x)=2f(x)f′(x),将f′(x)=f2(x)代入,得f′′(x)=2f3(x)。只有A满足此规律(排除法。下图见填空题【归纳法】)

法二(特殊函数法):令 f ( x ) = − 1 x f(x)=-\dfrac{1}{x} f(x)=−x1。求导得 f ′ ( x ) = 1 x 2 , f ′ ′ ( x ) = − 2 x 3 , f ′ ′ ′ ( x ) = 6 x 4 f'(x)=\dfrac{1}{x^2},f''(x)=-\dfrac{2}{x^3},f'''(x)=\dfrac{6}{x^4} f′(x)=x21,f′′(x)=−x32,f′′′(x)=x46,按照规律,应为A
2.4 隐函数及参数方程的导数
隐函数的导数
由参数方程所确定的函数的导数
含绝对值的导数
①先求极限,求出f(x)的分段函数表达式。注意an需要对底数a进行分类讨论
②对分段函数的分段点的可导性进行讨论。用导数定义。
2.5 一元可微
法1:画图法
由上图的一元可微图可知,0
Ch3.中值定理
费马引理
罗尔定理
(1)在闭区间 [a,b] 上连续
(2)在开区间 (a,b) 内可导
(3)在区间端点处的函数值相等,即 f(a)=f(b)
那么在开区间 (a,b) 内至少有一点ξ (a<ξ

拉格朗日中值定理
(1)在闭区间 [a,b] 上连续
(2)在开区间 (a,b) 内可导
那么在开区间 (a,b) 内至少有一点ξ (a<ξ
f ( b ) − f ( a ) = f ′ ( ξ ) ( b − a ) ( a < ξ < b ) 或 f ′ ( ξ ) = f ( b ) − f ( a ) b − a ( a < ξ < b ) f(b)-f(a)=f'(ξ)(b-a)\qquad (a<ξ

柯西中值定理
洛必达法则
洛就完了。
泰勒公式
泰勒中值定理1:
泰勒中值定理2:
麦克劳林公式
原式
泰勒展开 (写到3阶)
e x e^x ex
1 + x + x 2 2 ! + x 3 3 ! + o ( x 3 ) 1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+o(x^3) 1+x+2!x2+3!x3+o(x3)
sin x \sin x sinx
x − x 3 3 ! + x 5 5 ! + o ( x 5 ) x-\dfrac{x³}{3!}+\dfrac{x^5}{5!}+o(x^5) x−3!x3+5!x5+o(x5)
cos x \cos x cosx
1 − x 2 2 ! + x 4 4 ! + o ( x 4 ) 1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}+o(x^4) 1−2!x2+4!x4+o(x4)
t a n x {\rm tan}x tanx
x + x 3 3 + o ( x 3 ) x+\dfrac{x³}{3}+o(x³) x+3x3+o(x3)
1 1 − x \dfrac{1}{1-x} 1−x1
1 + x + x 2 + x 3 + o ( x 3 ) 1+x+x^2+x^3+o(x^3) 1+x+x2+x3+o(x3)
1 1 + x \dfrac{1}{1+x} 1+x1
1 − x + x 2 − x 3 + o ( x 3 ) 1-x+x^2-x^3+o(x^3) 1−x+x2−x3+o(x3)
ln ( 1 + x ) \ln(1+x) ln(1+x)
x − x 2 2 + x 3 3 − x 4 4 + . . . + ( − 1 ) n + 1 x n n + o ( x n ) x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\dfrac{x^4}{4}+...+(-1)^{n+1}\dfrac{x^n}{n}+o(x^n) x−2x2+3x3−4x4+...+(−1)n+1nxn+o(xn)
1 1 + x 2 \dfrac{1}{1+x^2} 1+x21
1 − x 2 + x 4 − x 6 + o ( x 3 ) 1-x^2+x^4-x^6+o(x^3) 1−x2+x4−x6+o(x3)
a r c t a n x {\rm arctan}x arctanx
x − x 3 3 + o ( x 3 ) x-\dfrac{x^3}{3}+o(x^3) x−3x3+o(x3)
![]()
答案:D

极值与拐点
极值
设函数f(x)在点 x 0 x_0 x0的某邻域 U ( x 0 ) U(x_0) U(x0)内有定义,如果对于去心邻域 U ˚ ( x 0 ) Ů(x_0) U˚(x0)内的任一x,恒有 f ( x ) < f ( x 0 ) f(x)
①驻点,即 f ′ ( x ) = 0 f'(x)=0 f′(x)=0
②不可导点,即 f ′ ( x ) f'(x) f′(x)不存在
设函数 f ( x ) f(x) f(x)在 x 0 x₀ x0处连续,且在 x 0 x₀ x0的去心邻域 U ˚ ( x 0 , δ ) Ů(x₀,δ) U˚(x0,δ)内可导
(1)若 x ∈ ( x 0 − δ , x 0 ) x∈(x₀-δ,x₀) x∈(x0−δ,x0)时, f ′ ( x ) > 0 f'(x)>0 f′(x)>0,而 x ∈ ( x 0 , x 0 + δ ) x∈(x₀,x₀+δ) x∈(x0,x0+δ)时, f ′ ( x ) < 0 f'(x)<0 f′(x)<0,则 f ( x ) f(x) f(x)在 x 0 x₀ x0处取得 极大值
(2)若 x ∈ ( x 0 − δ , x 0 ) x∈(x₀-δ,x₀) x∈(x0−δ,x0)时, f ′ ( x ) < 0 f'(x)<0 f′(x)<0,而 x ∈ ( x 0 , x 0 + δ ) x∈(x₀,x₀+δ) x∈(x0,x0+δ)时, f ′ ( x ) > 0 f'(x)>0 f′(x)>0,则 f ( x ) f(x) f(x)在 x 0 x₀ x0处取得 极小值
(3)若 x ∈ U ˚ ( x 0 , δ ) x∈Ů(x₀,δ) x∈U˚(x0,δ)时, f ′ ( x ) f'(x) f′(x)的符号保持不变,则 f ( x ) f(x) f(x)在 x 0 x₀ x0处 没有极值
设函数f(x)在 x 0 x_0 x0处具有二阶导数且 f ′ ( x 0 ) = 0 , f ′ ′ ( x 0 ) ≠ 0 f'(x_0)=0,f''(x_0)≠0 f′(x0)=0,f′′(x0)=0,则
(1)当 f ′ ( x ) = 0 , f ′ ′ ( x 0 ) < 0 f'(x)=0,f''(x_0)<0 f′(x)=0,f′′(x0)<0时,函数f(x)在 x 0 x_0 x0处取得极大值
(2)当 f ′ ( x ) = 0 , f ′ ′ ( x 0 ) > 0 f'(x)=0,f''(x_0)>0 f′(x)=0,f′′(x0)>0时,函数f(x)在 x 0 x_0 x0处取得极小值
显然:
①驻点a为极大值点
②驻点b为极小值点
③不可导点0,由极值的第一充分条件,得x=0为极大值点
④驻点c为极小值点

分析:

拐点
凹:① f ( x 1 + x 2 2 ) < f ( x 1 ) + f ( x 2 ) 2 f(\dfrac{x_1+x_2}{2})<\dfrac{f(x_1)+f(x_2)}{2} f(2x1+x2)<2f(x1)+f(x2) ② f ′ ′ ( x ) > 0 f''(x)>0 f′′(x)>0![]()
(1) f ′ ( x ) f'(x) f′(x) 在 x 0 x_0 x0处改变增减性,即 x 0 x_0 x0左右两侧 f ′ ′ ( x ) f''(x) f′′(x) 异号
(2) f ′ ′ ( x 0 ) = 0 , f ′ ′ ′ ( x 0 ) ≠ 0 f''(x_0)=0,f'''(x_0)≠0 f′′(x0)=0,f′′′(x0)=0
极值点 vs 拐点
区别
极值点的必要条件
一阶导数的零点(驻点)或者瑕点
拐点的必要条件
二阶导数的零点或者瑕点
偶数阶导数不为0:极值点 ;举例: f ′ ( x 0 ) = f ′ ′ ( x 0 ) = f ′ ′ ′ ( x 0 ) = 0 , f ( 4 ) ( x 0 ) ≠ 0 f'(x_0)=f''(x_0)=f'''(x_0)=0,f^{(4)}(x_0)≠0 f′(x0)=f′′(x0)=f′′′(x0)=0,f(4)(x0)=0,则 x 0 x_0 x0为极值点
①拐点的必要条件(可能为拐点的点):f’‘(x)=0或 f’‘(x)不存在。有三个点x=a,x=0,x=b
②拐点的充分条件:f’‘(x)在该点处左右的负号改变,显然排除x=a,剩余两个x=0,x=b满足f’'(x)负号改变,是拐点
②一个点不可能同时为极值点和拐点:若为极值点,则不会是拐点。若为拐点,则不会是极值点。

1点的凹凸性没有发生改变,排除A

分析: 求拐点:二阶导=0

可能为拐点(拐点的必要条件):f’‘(x)=0或f’‘(x)不存在
f’‘(x)=0:x=-1
f’'(x)不存在:x=0
渐近线
铅直渐近线
水平渐近线
则称 y = c y=c y=c为曲线 y = f ( x ) y=f(x) y=f(x)的水平渐近线
斜渐近线
或者 lim x → − ∞ f ( x ) x = a ≠ 0 \lim\limits_{x→-∞}\dfrac{f(x)}{x}=a≠0 x→−∞limxf(x)=a=0 且 lim x → − ∞ f ( x ) − a x = b \lim\limits_{x→-∞}f(x)-ax=b x→−∞limf(x)−ax=b
则称 y = a x + b y=ax+b y=ax+b为曲线 y = f ( x ) y=f(x) y=f(x)的斜渐近线
函数f(x)
铅直
水平
斜
A : y = x + s i n x A:y=x+sinx A:y=x+sinx
×
×
× 有a无b
B : y = x 2 + s i n x B:y=x²+sinx B:y=x2+sinx
×
×
× 无a
C : y = x + s i n 1 x C:y=x+sin\dfrac{1}{x} C:y=x+sinx1
×
×
√ 有a有b
D : y = x 2 + s i n 1 x D:y=x²+sin\dfrac{1}{x} D:y=x2+sinx1
×
×
× 无a

由 y = s i n 1 x y=sin\dfrac{1}{x} y=sinx1图像可知, y = s i n 1 x y=sin\dfrac{1}{x} y=sinx1在x=0处是有界振荡,不存在无穷间断点,故没有铅直渐近线。
曲率、曲率半径
Ch4.不定积分
Ch5.定积分
Ch6.定积分应用
Ch7.微分方程