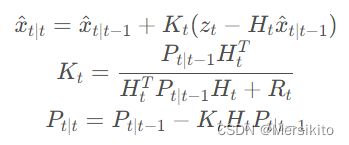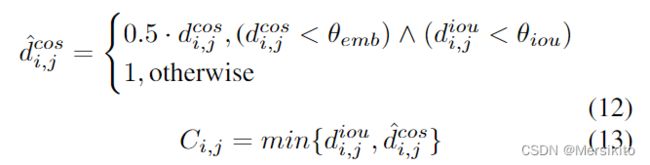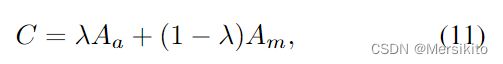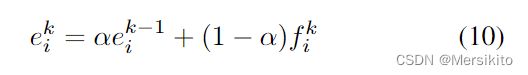【论文阅读5】BoT-SORT：Robust Associations Multi-Pedestrian Tracking

【论文阅读5】BoT-SORT：Robust Associations Multi-Pedestrian Tracking

和OC-SORT类似，BoT-SORT也是对Kalman滤波进行改进。OCSORT是针对：对于未匹配的轨迹（由于遮挡等原因），Kalman滤波的状态估计方差会变大，进而导致误差累积的问题，对轨迹做了平滑。

而BoT-SORT针对Kalman滤波有两点改进：

1. 改进Kalman滤波中的状态变量
2. 针对相机运动的问题，加入了相机运动补偿。也就是除了利用Kalman预测轨迹的新位置之外，还利用稀疏光流(也就是提取目标之外的画面中的关键点），来获得两帧之间画面的移动，进而补偿Kalman的状态估计。

1. 各部分笔记

1.1 Abstract & Introduction

大多数SORT-like算法采用卡尔曼滤波器，并将等速模型假设作为运动模型。KF用于预测tracklet在下一帧中的边界框，以便与检测边界框关联，并在发生遮挡或未检测到的情况下预测tracklet的状态。

与由目标检测器驱动的检测相比，使用KF的状态估计作为跟踪器的输出会导致次优边界框形状。最近的大多数方法使用了经典跟踪器DeepSORT中提出的KF状态表征，该方法试图估计盒子的纵横比而不是宽度，这导致了不准确的宽度大小估计。

SORT-like算法主要取决于tracklet的预测边界框（Kalman滤波的状态估计）的质量。因此，在许多复杂场景中，由于相机运动，预测边界框的位置可能会出现偏移，这会导致两个相关边界框之间的重叠较低，最终导致跟踪器性能较低。通过采用传统的图像配准来估计摄像机运动，并适当地校正卡尔曼滤波器的状态估计，来克服这一问题。我们将其称为相机运动补偿（CMC）。

在许多情况下，SORT-like算法中的定位和外观信息（即Re-ID）导致跟踪器的检测能力（MOTA）和跟踪器随时间保持正确身份的能力（IDF1）之间的权衡。使用IoU通常实现更好的MOTA，而Re-ID实现更高的IDF1。

---

本文的贡献如下：

1. 通过 改进Kalman滤波中的状态变量 和 增加相机运动补偿，可以提高Kalman滤波的状态估计（tracklet的预测边界框）的质量。
2. 为 两种关联度量（IoU距离和Re-ID特征的余弦距离）的融合 提出了一种简单有限的方法，实现检测和轨迹之间更鲁棒的关联。

1.2 Proposed Method

1.2.1 改进Kalman滤波中的状态变量

Kalman滤波遵循如下的预测和更新步骤：

其中 $Q$ 表示状态噪声的协方差矩阵，$R$ 表示观测噪声的协方差矩阵。

---

状态变量的选择：

SORT的状态变量为[中心点x坐标，中心点y坐标，面积，高宽比，x轴速度，y轴速度，面积变化速率]，即 $x=[x_c,y_c,s,a,{\dot{x}}_c,{\dot{y}}_c,\dot{s}]$

从DeepSORT之后，状态变量基本采用的是 $x=[x_c,y_c,a,h,{\dot{x}}_c,{\dot{y}}_c,\dot{a},\dot{h}]$

在BoT-SORT中，作者简单地将状态变量改成了 $xywh$ 及其对时间的导数，即 $x=[x_c,y_c,w,h,{\dot{x}}_c,{\dot{y}}_c,\dot{w},\dot{h}]$。相应地，观测向量为 $z=[z_{x_c},z_{y_c},z_w,z_h]$

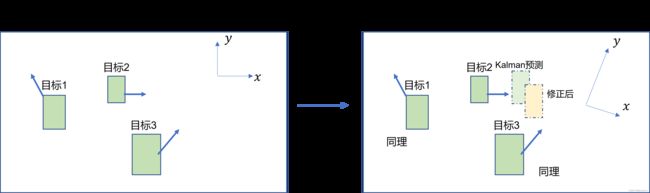
1.2.2 相机运动补偿（CMC）

Tracking-by-detection算法的性能在很大程度上依赖于tracklet的预测边界框（Kalman滤波的状态估计）的质量。

视频中的运动模式可以总结为：相机的刚性运动 以及 目标的非刚性运动

目标变换常见的可以分为刚性运动和非刚性运动，刚性运动即目标的位置和方向发生变化，非刚性运动则是指目标的形状发生变化，包括尺度变换，缩放变换，透视变换。

在动态相机场景中，图像平面中的边界框位置可能会发生剧烈变化，这可能会导致ID switches 或 False Negatives 增加。静态相机场景中的跟踪器也可能因风引起的振动或漂移而受到影响。

由于缺乏相机运动的先验信息，因此，相邻两帧之间的图像配准可以近似相机的刚性运动在图像二维平面上的投影。

这里可以理解为，相机运动等同于坐标系的变换。我们需要将目标的位置、运动方向重新投影到新坐标系中，因此需要求解坐标系的变换矩阵。

因此, 利用 RANSAC算法得到平面坐标变化的仿射矩阵, 描述2维平面缩放和旋转变化矩阵为
，平移变化向量为
，定义仿射矩阵为：

1.2.3 两种关联度量（IoU距离和Re-ID特征的余弦距离）的融合

在匹配过程中, 利用指数滑动平均来平衡过去和当前的外观特征，随后将运动特征和外观特征线性组合作为cost matrix, 如下式所示：

对于外观和IoU都相似的目标, 给予更小的cost, 否则设为1, 并以此更新C中的元素：

谁可靠就考虑谁。