第一章:全世界最简单的机器学习入门指南 https://blog.csdn.net/wskzgz/article/details/89917343
第二章:用机器学习制作超级马里奥的关卡 https://blog.csdn.net/wskzgz/article/details/89945137
第三章:图像识别-深度学习与卷积神经网络 https://blog.csdn.net/wskzgz/article/details/89945534
第四章:用深度学习识别人脸 https://blog.csdn.net/wskzgz/article/details/90065758

首发于 离线
作者:Adam Geitgey
原文:https://medium.com/@ageitgey/machine-learning-is-fun-80ea3ec3c471#.ak1of1xbg
翻译:巡洋舰科技——赵95
校对:离线Offline——林沁
转载请联系译者。
你是否曾经听到过人们谈论机器学习,而你却对其含义只有一个模糊的概念呢?你是否已经厌倦了在和同事对话时只能点头呢?现在,让我们一起来改变这个现状吧!
这篇指南是为那些对机器学习感兴趣,但又不知从哪里开始的人而写的。我猜有很多人曾经尝试着阅读机器学习的维基百科词条,但是读着读着倍感挫折,然后直接放弃,希望能有人给出一个更直观的解释。本文就是你们想要的东西。
本文的写作目标是让任何人都能看懂,这意味着文中有大量的概括。但是那又如何呢?只要能让读者对机器学习更感兴趣,这篇文章的任务也就完成了。
什么是机器学习?
机器学习是一种概念:不需要写任何与问题有关的特定代码,泛型算法(Generic Algorithms)[1]就能告诉你一些关于你数据的有趣结论。不用编码,你将数据输入泛型算法当中,它就会在数据的基础上建立出它自己的逻辑。
比如说,有一种算法被称为分类算法,它可以将数据分为不同的组。分类算法可以用来识别手写数字;不用修改一行代码,它也可以用来区分垃圾邮件和非垃圾邮件。如果给同样的算法输入不同的训练数据,它就能得出不同的分类逻辑。


机器学习算法是个黑盒,它可以重复使用于很多不同的分类问题。
「机器学习」是一个涵盖性术语,它覆盖了大量类似的泛型算法。
两类机器学习算法
你可以把机器学习算法分为两大类:监督式学习(supervised Learning)和非监督式学习(unsupervised Learning)。要区分两者很简单,但也非常重要。
监督式学习
假设你是一名房地产经纪人,你的生意蒸蒸日上,因此你雇了一批新员工来帮忙。但是问题来了——虽然你可以一眼估算出房子的价格,但新员工却不像你这样经验丰富,他们不知道如何给房子估价。
为了帮助你的新员工(也许就是为了给自己放个假嘻嘻),你决定写一个可以根据房屋大小、地段以及同类房屋成交价等因素来评估一间房屋的价格的小软件。
近三个月来,每当你的城市里有人卖了房子,你都记录了下面的细节——卧室数量、房屋大小、地段等等。但最重要的是,你写下了最终的成交价:


这就是我们的「训练数据」。
使用这些训练数据,我们要来编写一个能够估算该地区其他房屋价值的程序:


我们希望使用这些训练数据来预测其他房屋的价格。
这就是监督式学习。你已经知道了每一栋房屋的售价,换句话说,你已经知道了问题的答案,并且可以反向找出解题的逻辑。
为了编写你的软件,你将包含每一套房产的训练数据输入到你的机器学习算法当中去。算法会尝试找出需要做哪些数学运算来得出价格。
这就好像是你已经知道了数学测试题的答案,但是算式中的运算符号都被擦去了:
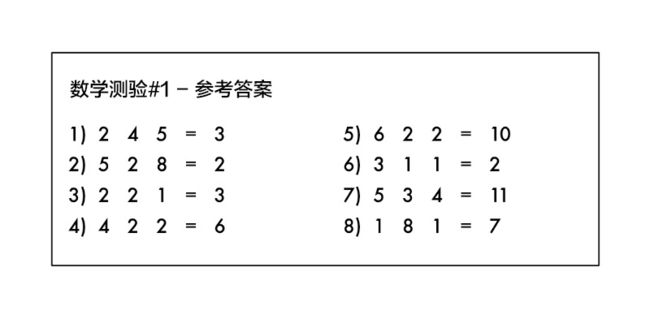

天啊!一个阴险的学生擦去了参考答案上的算术符号!
你能从这张图里看出来测验中的数学题是怎样的吗?你知道自己应该对左边的数字「做些什么」,才能得到右边的答案。
在监督式学习中,你让计算机为你算出这种关系。而一旦你知道了解决这类特定问题所需要的数学方法后,你就可以解答其它同类问题了!
非监督式学习
让我们回到房地产经纪人的例子。如果你不知道每栋房子的售价怎么办?即使你所知道的仅仅是每栋房屋的大小、位置等信息,你也可以搞出一些很酷炫的花样来。这就是我们所说的非监督式学习。


即使你并不是在尝试预测未知的数据(如价格),你也可以运用机器学习做一些有意思的事。
这就有点像有人给你一张纸,上面写了一列数字,然后说:「我不太清楚这些数字有什么意义,但也许你能找出些规律或是把它们分类什么的——祝你好运!」
所以该怎么处理这些数据呢?首先,你可以用个算法自动从数据中划分出不同的细分市场。也许你会发现,当地大学附近的购房者特喜欢户型小、卧室多的房子,而郊区的购房者偏好三卧室的大户型。了解这些不同消费者的喜好可以直接帮助你的营销。
你还可以做件很酷炫的事,就是自动找出非同寻常的房屋。这些与众不同的房产也许是奢华的豪宅,而你可以将最优秀的销售人员集中在这些地区,因为他们的佣金更高。
在接下来的内容中我们主要讨论监督式学习,但这并不是因为非监督式学习比较没用或是无趣。实际上,随着算法的改良,非监督式学习正变得越来越重要,因为即使不将数据和正确答案联系在一起,它也可以被使用。[2]
太酷炫了,但是估算房价真能被看作「学习」吗?
作为人类的一员,你的大脑可以应付绝大多数情况,并且在没有任何明确指令时也能够学习如何处理这些情况。如果你做房地产经纪人时间足够长,你对于房产的合适定价、房屋的最佳营销方式以及客户会感兴趣类型等等都会有一种本能般的「感觉」。强人工智能研究的目标就是要计算机复制这种能力。
但是目前的机器学习算法还没有那么强大——它们只能在非常特定的、有限的问题上有效。也许在这种情况下,「学习」更贴切的定义是「在少量样本数据的基础上找出一个公式来解决特定的问题」。
但是「机器在少量样本数据的基础上找出一个公式来解决特定的问题」不是个好名字。所以最后我们用「机器学习」取而代之。
当然了,如果你是在 50 年后的未来读的这篇文章,而我们人类也已经得出了强人工智能的算法的话,那这篇文章看起来就像个老古董了。那样的话,就别读了,去让你的机器佣人给你做份三明治吧,未来的人类。
让我们愉快地写代码吧!
所以,你打算怎么写上面例子中评估房价的程序呢?在往下看之前先思考一下吧。
如果对机器学习一无所知,你很有可能会尝试写出一些基本规则来评估房价,如下:
def
estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):
price = 0
# 在我这地方,每平方英尺房屋均价是 200 美元
price_per_sqft = 200
if
neighborhood == “hipsterton”:
#
但是有些地段房价会贵一点
price_per_sqft = 400
elif neighborhood == “skid row”:
#
有些地段房价便宜点
price_per_sqft = 100
# 我们先按面积大小估计房屋价格基准
price = price_per_sqft * sqft
# 现在根据卧室数量微调价格
if
num_of_bedrooms == 0:
#
工作室类型的公寓比较便宜
price = price — 20000
else:
#
卧室数量越多,通常房价越贵
price
= price + (num_of_bedrooms * 1000)
return price
假如你像这样瞎忙几个小时,最后也许会得到一些像模像样的东西。但是你的程序永不会完美,而且当价格变化时很难维护。
如果能让计算机找出实现上述函数功能的办法,岂不更好?只要返回的房价数字正确,谁会在乎函数具体干了些什么呢?
def
estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):
price = <计算机,请帮我算点数学题>
return price
考虑这个问题的一种角度是将价格看作一碗美味的汤,而汤的原材料就是卧室数量、面积和地段。如果你能算出每种原材料对最终的价格有多大影响,也许就能得到各种原材料混合形成最终价格的具体比例。
这样可以将你最初的程序(全是令人抓狂的 if else 语句)简化成类似如下的样子:
def
estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):
price = 0
# 一小撮这个
price += num_of_bedrooms * .841231951398213
# 一大撮那个
price += sqft * 1231.1231231
# 或许再加一把这个
price += neighborhood * 2.3242341421
# 最后,再多加一点点盐
price += 201.23432095
return price
注意那些用粗体标注的神奇数字——.841231951398213, 1231.1231231, 2.3242341421, 和201.23432095。它们称为权重(weight)。如果我们能找出对每栋房子都适用的完美权重,我们的函数就能预测所有的房价![3]
一种找出最佳权重的笨办法如下所示:
第一步:
首先,将每个权重都设为 1.0:
def
estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):
price = 0
# 一小撮这个
price += num_of_bedrooms * 1.0
# 一大撮那个
price += sqft * 1.0
# 或许再加一把这个
price += neighborhood * 1.0
# 最后,再多加一点点盐
price += 1.0
return price
第二步:
将你知道的每栋房产的数据代入函数进行运算,检验估算值与正确价格的偏离程度:


用你的程序来预测每栋房屋的价格。
比如说,如果第一套房产实际成交价为 25 万美元,你的函数估价为 17.8 万美元,这一套房产你就差了 7.2 万。
现在,将你的数据集中的每套房产估价偏离值平方后求和。假设你的数据集中交易了 500 套房产,估价偏离值平方求和总计为 86,123,373 美元。这个数字就是你的函数现在的「错误」程度。
现在,将总和除以 500,得到每套房产的估价偏差的平均值。将这个平均误差值称为你函数的代价(cost)。
如果你能通过调整权重,使得这个代价变为 0,你的函数就完美了。它意味着,根据输入的数据,你的程序对每一笔房产交易的估价都是分毫不差。所以这就是我们的目标——通过尝试不同的权重值,使代价尽可能的低。
第三步:
通过尝试所有可能的权重值组合,不断重复第二步。哪一个权重组合的代价最接近于 0,你就使用哪个。当你找到了合适的权重值,你就解决了问题!
兴奋的时刻到了!
挺简单的,对吧?想一想刚才你做了些什么。你拿到了一些数据,将它们输入至三个泛型的、简单的步骤中,最后你得到了一个可以对你所在区域任何房屋进行估价的函数。房价网站们,你们要小心了!
但是下面的一些事实可能会让你更兴奋:
1. 过去 40 年来,很多领域(如语言学、翻译学)的研究表明,这种「搅拌数字汤」(我编的词)的泛型学习算法已经超过了那些真人尝试明确规则的方法。机器学习的「笨」办法终于打败了人类专家。
2. 你最后写出的程序是很笨的,它甚至不知道什么是「面积」和「卧室数量」。它知道的只是搅拌,改变数字来得到正确的答案。
3. 你可能会对「为何一组特殊的权重值会有效」一无所知。你只是写出了一个你实际上并不理解却能证明有效的函数。
4. 试想,如果你的预测函数输入的参数不是「面积」和「卧室数量」,而是一列数字,每个数字代表了你车顶安装的摄像头捕捉的画面中的一个像素。然后,假设预测的输出不是「价格」而是「方向盘转动角度」,这样你就得到了一个程序可以自动操纵你的汽车了!
太疯狂了,对吧?[4]
第三步里「尝试每个数字」是怎么一回事?
好吧,当然你不可能试遍所有权重组合来找到效果最好的组合。直到世界毁灭你也算不完,因为这数字和组合无穷无尽。
为了避免这种情况,数学家们找到了很多种聪明的办法来快速找到优秀的权重值。下面是一种:
首先,写出一个简单的等式表示上面的第二步:


这就是你的代价函数(Cost Function)。
现在让我们,使用机器学习数学术语(现在暂时你可以忽略它们),重新改写同样的这一等式:


θ 表示当前的权重值。 J(θ) 表示「当前权重的代价」。
这个等式表示,在当前权重值下,我们估价程序的偏离程度。
如果我们为这个等式中所有卧室数和面积的可能权重值作图的话,我们会得到类似下图的图表:


我们代价函数的图形就像一个碗。纵轴表示代价。
图中,蓝色的最低点就是代价最低的地方——在这里我们的程序偏离最小。最高点们意味着偏离最大。所以,如果我们能找到一组权重值让我们到达图中的最低点,我们就得到了答案!


因此,我们需要做的只是调整我们的权重,使得我们在图上朝着最低点「走下坡路」。如果我们不断微调权重,一直向最低点移动,那么我们最终不用尝试太多权重就可以到达那里。
如果你还记得一点微积分的话,你也许记得如果你对一个函数求导,它会告诉你函数任意一点切线的斜率。换句话说,对于图上任意给定的一点,求导能告诉我们哪条是下坡路。我们可以利用这个知识不断走向最低点。[5]
所以,如果我们对代价函数关于每一个权重求偏导,那么我们就可以从每一个权重中减去该值。这样可以让我们更加接近山底。一直这样做,最终我们将到达底部,得到权重的最优值。(读不懂?不用担心,继续往下读)。
这种为函数找出最佳权重的方法叫做批量梯度下降(Batch Gradient Descent)。如果你对细节感兴趣,不要害怕,可以看看这个详细说明。
当你使用一个机器学习算法库来解决实际问题时,这些都已经为你准备好了。但清楚背后的原理依然是有用的。
还有什么是本篇文章略过的内容?
上面我描述的三步算法被称为多元线性回归(multivariate linear regression)。你在估算一个能够拟合所有房价数据点的直线表达式。然后,你再根据房子可能在你的直线上出现的位置,利用这个等式来估算你从未见过的房屋的价格。这是一个十分强大的想法,你可以用它来解决「实际」问题。
但是,尽管我展示给你的这种方法可能在简单的情况下有效,它却不能应用于所有情况。原因之一,就是因为房价不会是简简单单一条连续的直线。
不过幸运的是,有很多办法来处理这种情况。有许多机器学习算法可以处理非线性数据(如神经网络或带核函数的支持向量机)。除此之外,灵活使用线性回归也能拟合更复杂的线条。在所有的情况下,寻找最优权重这一基本思路依然适用。
另外,我忽略了过拟合(overfitting)的概念。得到一组能完美预测原始数据集中房价的权重组很简单,但用这组权重组来预测原始数据集之外的任何新房屋其实都不怎么准确。这也是有许多解决办法的(如正则化以及使用交叉验证的数据集)。学习如何应对这一问题,是学习如何成功应用机器学习技术的重点之一。
换言之,尽管基本概念非常简单,要通过机器学习得到有用的结果还是需要一些技巧和经验的。但是,这是每个开发者都能学会的技巧。
机器学习是黑魔法吗?
一旦你开始明白,用机器学习技术解决那些看似困难问题(如字迹识别)有多便利时,你就会有一种,只要有足够的数据,你就能够用机器学习解决任何问题的感觉。只需要输入数据,计算机就能神奇地找出拟合数据的等式!
但是有一点很重要,你要记住,只有在你拥有的数据对于解决实际问题有效的时候,机器学习才能适用。
例如,如果你建立了一个根据每套房屋内盆栽种类的数量来预测房价的模型,那它永远都不会有效果。因为盆栽种类的数量和房价之间没有任何的关系。所以,无论你多卖力地尝试,计算机永远也推导不出两者之间的关系。


你只能模拟实际存在的关系。
所以请记住,如果一个问题人类专家不能手动用数据解决,计算机可能也不能解决。然而,对于那些人类能够解决的问题,如果计算机能够更快地解决,那岂不美哉?
怎样学到更多机器学习的知识
我认为,目前机器学习的最大问题是它主要活跃于学术界和商业研究组织中。对于只想大体了解一下,而不打算成为专家的人们来说,简单易懂的资料不多。但是这种情况每天正在改善。
吴恩达教授(Andrew Ng)在 Coursera 上的免费机器学习课程非常棒。我强烈建议从此入手。对于任何拥有计算机或科学学位的人,或是还能记住一点点数学的人来说,都应该非常容易入门。
另外,你还可以通过下载安装 SciKit-Learn,用它来试验无数个机器学习算法。它是一个 Python 框架,包含了所有常见机器学习算法的「黑盒」版本。
注:
1. 译者注:泛型,即没有特定类型,泛型算法是一种对很多不同问题都适用的算法,也叫作通用算法。如果你现在还对这个概念一知半解没关系,相信你读过这篇文章之后会对「泛型算法」有一个更深入的理解。
2. 作者注:还有很多其它种类的机器学习算法。但从这里开始讲起是一个不错的选择。
3. 译者注:权重可能有很多种不同的组合,每一种权重最后给出的房价预测也不同,我们的目标就是要找出一组最终价格最接近真实值的权重。
4. 译者注:到这里,你应该对泛型算法有一个更深刻的理解了。
5. 译者注:如果你还记得微积分当中,一个点求出的导数是 0的话,那么这个点就是最低点。所以返回到刚刚的代价函数里面,代价函数就等于 0,也就意味着,你的预估和真实值没有任何差别。
编辑于 2017-02-03


























49 条评论
要看你的函数,在这里这个代价函数就是一个碗的形状。并且你说的也对,所以我们不只是用导数为零来求最低点,感兴趣的话可以看看下降梯度法。
这不是Ng大神的例子么。。。