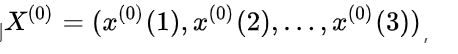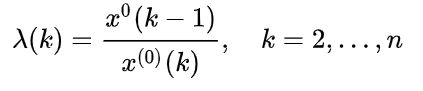（九）预测模型
| 预测模型名称 |
适用范围 |
优点 |
缺点 |
| 灰色预测模型 |
该模型使用的不是原始数据的序列，而是生成的数据序列。核心体系是Grey Model.即对原始数据作累加生成（或其他处理生成）得到近似的指数规律再进行建模的方法。 |
在处理较少的特征值数据，不需要数据的样本空间足够大，就能解决历史数据少、序列的完整性以及可靠性低的问题，能将无规律的原始数据进行生成得到规律较强的生成序列。 |
只适用于中短期的预测，只适合近似于指数增长的预测。 |
| 插值与拟合 |
适用于有物体运动轨迹图像的模型。如导弹的运动轨迹测量的建模分析。 |
分为曲面拟合和曲线拟合，拟合就是要找出一种方法（函数）使得得到的仿真曲线（曲面）最大程度的接近原来的曲线（曲线），甚至重合。这个拟合的好坏程度可以用一个指标来判断。 |
|
| 时间序列预测法 |
根据客观事物发展的这种连续规律性，运用过去的历史数据，通过统计分析，进一步推测市场未来的发展趋势。时间序列在时间序列分析预测法处于核心位置。 |
一般用ARMA模型拟合时间序列，预测该时间序列未来值。 Daniel检验平稳性。 自动回归AR(Auto regressive)和移动平均MA(Moving Average)预测模型。 |
当遇到外界发生较大变化，往往会有较大偏差，时间序列预测法对于中短期预测的效果要比长期预测的效果好。 |
| 神经元网络 |
数学建模中常用的是BP神经网络和径向基函数神经网络的原理，及其在预测中的应用。 BP神经网络拓扑结构及其训练模式。 RBF神经网络结构及其学习算法。 模型案例：预测某水库的年径流量和因子特征值 |
||
一.灰色预测概述
灰色预测是用灰色模型GM(1,1)来进行定量分析的，通常分为以下几类：
(1) 灰色时间序列预测。用等时距观测到的反映预测对象特征的一系列数量（如产量、销量、人口数量、存款数量、利率等）构造灰色预测模型，预测未来某一时刻的特征量，或者达到某特征量的时间。
(2) 畸变预测（灾变预测）。通过模型预测异常值出现的时刻，预测异常值什么时候出现在特定时区内。
(3) 波形预测，或称为拓扑预测，它是通过灰色模型预测事物未来变动的轨迹。
(4) 系统预测，对系统行为特征指标建立一族相互关联的灰色预测理论模型，在预测系统整体变化的同时，预测系统各个环节的变化。
上述灰色预测方法的共同特点是：
（1）允许少数据预测；
（2）允许对灰因果律事件进行预测，例如：
灰因白果律事件：在粮食生产预测中，影响粮食生产的因子很多，多到无法枚举，故为灰因，然而粮食产量却是具体的，故为白果。粮食预测即为灰因白果律事件预测。
白因灰果律事件：在开发项目前景预测时，开发项目的投入是具体的，为白因，而项目的效益暂时不很清楚，为灰果。项目前景预测即为灰因白果律事件预测。
（3）具有可检验性，包括：建模可行性的级比检验（事前检验），建模精度检验（模型检验），预测的滚动检验（预测检验）。
2.GM(1,1)模型理论
GM(1,1)模型适合具有较强的指数规律的数列，只能描述单调的变化过程。
3.算法步骤
(1) 数据的级比检验
为了保证灰色预测的可行性，需要对原始序列数据进行级比检验。
对原始数据列
，计算序列的级比： 
若所有的级比
都落在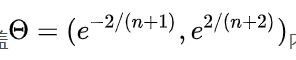
可容覆盖内，则可进行灰色预测；否则需要对
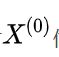做平移变换，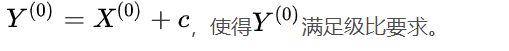
(2) 建立GM(1,1)模型，计算出预测值列。
(3) 检验预测值：
① 相对残差检验，计算
灰色建模的主体应该分为几步：
（1）引入、整理数据
（2）校验数据是否合格
（3）GM(1,1)建模
（4）将最新的预测数据当做真实值继续预测
（5）输出结果
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
def GM11(x, n):
'''
灰色预测
x：序列，numpy对象
n:需要往后预测的个数
'''
x1 = x.cumsum() # 一次累加
z1 = (x1[:len(x1) - 1] + x1[1:]) / 2.0 # 紧邻均值
z1 = z1.reshape((len(z1), 1))
B = np.append(-z1, np.ones_like(z1), axis=1)
Y = x[1:].reshape((len(x) - 1, 1))
# a为发展系数 b为灰色作用量
[[a], [b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Y) # 计算参数
result = (x[0] - b / a) * np.exp(-a * (n - 1)) - (x[0] - b / a) * np.exp(-a * (n - 2))
S1_2 = x.var() # 原序列方差
e = list() # 残差序列
for index in range(1, x.shape[0] + 1):
predict = (x[0] - b / a) * np.exp(-a * (index - 1)) - (x[0] - b / a) * np.exp(-a * (index - 2))
e.append(x[index - 1] - predict)
S2_2 = np.array(e).var() # 残差方差
C = S2_2 / S1_2 # 后验差比
if C <= 0.35:
assess = '后验差比<=0.35，模型精度等级为好'
elif C <= 0.5:
assess = '后验差比<=0.5，模型精度等级为合格'
elif C <= 0.65:
assess = '后验差比<=0.65，模型精度等级为勉强'
else:
assess = '后验差比>0.65，模型精度等级为不合格'
# 预测数据
predict = list()
for index in range(x.shape[0] + 1, x.shape[0] + n + 1):
predict.append((x[0] - b / a) * np.exp(-a * (index - 1)) - (x[0] - b / a) * np.exp(-a * (index - 2)))
predict = np.array(predict)
return {
'a': {'value': a, 'desc': '发展系数'},
'b': {'value': b, 'desc': '灰色作用量'},
'predict': {'value': result, 'desc': '第%d个预测值' % n},
'C': {'value': C, 'desc': assess},
'predict': {'value': predict, 'desc': '往后预测%d个的序列' % (n)},
}
if __name__ == "__main__":
data = np.array([1.2, 2.2, 3.1, 4.5, 5.6, 6.7, 7.1, 8.2, 9.6, 10.6, 11, 12.4, 13.5, 14.7, 15.2])
x = data[0:10] # 输入数据
y = data[10:] # 需要预测的数据
result = GM11(x, len(y))
predict = result['predict']['value']
predict = np.round(predict, 1)
print('真实值:', y)
print('预测值:', predict)
print(result)
二、插值预测【见（二）插值与拟合】
三、时间序列预测【见（八）时间序列预测模型】
四、BP神经网络
1、概念
BP网络是一种多层前馈神经网络,它的名字源于在网络训练中,调整网络权值的训练算法是反向传播算法(即BP学习算法).
BP网络是一种具有三层或者三层以上神经元的神经网络,包括输入层,隐含层和输出层,上下层之间实现全连接,而同一层的神经元之间无连接,输入层神经元和隐含层神经元之间的是网络的权值,即两个神经元之间的连接强度.隐含层或输出层任一神经元将前一层所有神经元传来的信息进行整合,通常还会在整合的信息中添加一个阈值.当一对学习样本提供给输入神经元后,神经元的激活值(该层神经元输出值)从输入层经过各隐含层向输出层传播,在输出层的各神经元获得网络的输入响应,然后按照减少网络输出与实际输出样本之间误差的方向,从输出层反向经过各隐含层回到输入层,从而逐步修正各隐含权值,这种算法称为误差反向传播算法,即BP算法.
2、求解过程
(1) 原始数据的输入
(2) 数据归一化
(3) 网络训练
(4) 对原始数据进行仿真
(5) 将原始数据仿真的结果与已知样本进行对比
(6) 对新数据进行仿真
3、代码
# -*- coding: utf-8 -*-
"""
Created on Mon Oct 1 22:15:54 2018
@author: Heisenberg
"""
import numpy as np
import math
import random
import string
import matplotlib as mpl
import matplotlib.pyplot as plt
#random.seed(0) #当我们设置相同的seed，每次生成的随机数相同。如果不设置seed，则每次会生成不同的随机数
#参考https://blog.csdn.net/jiangjiang_jian/article/details/79031788
#生成区间[a,b]内的随机数
def random_number(a,b):
return (b-a)*random.random()+a
#生成一个矩阵，大小为m*n,并且设置默认零矩阵
def makematrix(m, n, fill=0.0):
a = []
for i in range(m):
a.append([fill]*n)
return a
#函数sigmoid(),这里采用tanh，因为看起来要比标准的sigmoid函数好看
def sigmoid(x):
return math.tanh(x)
#函数sigmoid的派生函数
def derived_sigmoid(x):
return 1.0 - x**2
#构造三层BP网络架构
class BPNN:
def __init__(self, num_in, num_hidden, num_out):
#输入层，隐藏层，输出层的节点数
self.num_in = num_in + 1 #增加一个偏置结点
self.num_hidden = num_hidden + 1 #增加一个偏置结点
self.num_out = num_out
#激活神经网络的所有节点（向量）
self.active_in = [1.0]*self.num_in
self.active_hidden = [1.0]*self.num_hidden
self.active_out = [1.0]*self.num_out
#创建权重矩阵
self.wight_in = makematrix(self.num_in, self.num_hidden)
self.wight_out = makematrix(self.num_hidden, self.num_out)
#对权值矩阵赋初值
for i in range(self.num_in):
for j in range(self.num_hidden):
self.wight_in[i][j] = random_number(-0.2, 0.2)
for i in range(self.num_hidden):
for j in range(self.num_out):
self.wight_out[i][j] = random_number(-0.2, 0.2)
#最后建立动量因子（矩阵）
self.ci = makematrix(self.num_in, self.num_hidden)
self.co = makematrix(self.num_hidden, self.num_out)
#信号正向传播
def update(self, inputs):
if len(inputs) != self.num_in-1:
raise ValueError('与输入层节点数不符')
#数据输入输入层
for i in range(self.num_in - 1):
#self.active_in[i] = sigmoid(inputs[i]) #或者先在输入层进行数据处理
self.active_in[i] = inputs[i] #active_in[]是输入数据的矩阵
#数据在隐藏层的处理
for i in range(self.num_hidden - 1):
sum = 0.0
for j in range(self.num_in):
sum = sum + self.active_in[i] * self.wight_in[j][i]
self.active_hidden[i] = sigmoid(sum) #active_hidden[]是处理完输入数据之后存储，作为输出层的输入数据
#数据在输出层的处理
for i in range(self.num_out):
sum = 0.0
for j in range(self.num_hidden):
sum = sum + self.active_hidden[j]*self.wight_out[j][i]
self.active_out[i] = sigmoid(sum) #与上同理
return self.active_out[:]
#误差反向传播
def errorbackpropagate(self, targets, lr, m): #lr是学习率， m是动量因子
if len(targets) != self.num_out:
raise ValueError('与输出层节点数不符！')
#首先计算输出层的误差
out_deltas = [0.0]*self.num_out
for i in range(self.num_out):
error = targets[i] - self.active_out[i]
out_deltas[i] = derived_sigmoid(self.active_out[i])*error
#然后计算隐藏层误差
hidden_deltas = [0.0]*self.num_hidden
for i in range(self.num_hidden):
error = 0.0
for j in range(self.num_out):
error = error + out_deltas[j]* self.wight_out[i][j]
hidden_deltas[i] = derived_sigmoid(self.active_hidden[i])*error
#首先更新输出层权值
for i in range(self.num_hidden):
for j in range(self.num_out):
change = out_deltas[j]*self.active_hidden[i]
self.wight_out[i][j] = self.wight_out[i][j] + lr*change + m*self.co[i][j]
self.co[i][j] = change
#然后更新输入层权值
for i in range(self.num_in):
for i in range(self.num_hidden):
change = hidden_deltas[j]*self.active_in[i]
self.wight_in[i][j] = self.wight_in[i][j] + lr*change + m* self.ci[i][j]
self.ci[i][j] = change
#计算总误差
error = 0.0
for i in range(len(targets)):
error = error + 0.5*(targets[i] - self.active_out[i])**2
return error
#测试
def test(self, patterns):
for i in patterns:
print(i[0], '->', self.update(i[0]))
#权重
def weights(self):
print("输入层权重")
for i in range(self.num_in):
print(self.wight_in[i])
print("输出层权重")
for i in range(self.num_hidden):
print(self.wight_out[i])
def train(self, pattern, itera=100000, lr = 0.1, m=0.1):
for i in range(itera):
error = 0.0
for j in pattern:
inputs = j[0]
targets = j[1]
self.update(inputs)
error = error + self.errorbackpropagate(targets, lr, m)
if i % 100 == 0:
print('误差 %-.5f' % error)
#实例
def demo():
patt = [
[[1,2,5],[0]],
[[1,3,4],[1]],
[[1,6,2],[1]],
[[1,5,1],[0]],
[[1,8,4],[1]]
]
#创建神经网络，3个输入节点，3个隐藏层节点，1个输出层节点
n = BPNN(3, 3, 1)
#训练神经网络
n.train(patt)
#测试神经网络
n.test(patt)
#查阅权重值
n.weights()
if __name__ == '__main__':
demo()