Topsis模型小记
Topsis模型小记
一般步骤:
- 正向化(转化为极大型指标 )
- 标准化(求cos,去量纲)
- 计算得分并归一化(欧氏距离综合各个指标)
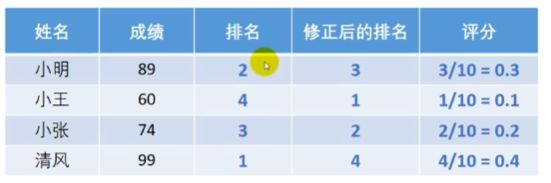
单个指标分析
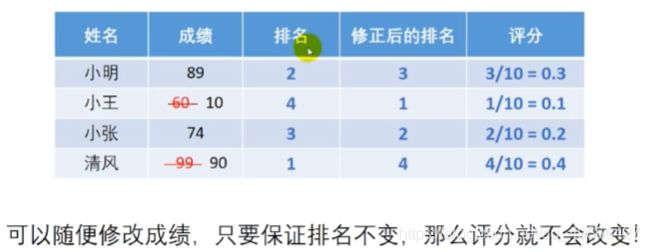
缺点在于,只看排名,分数发生巨大变化,但是排名不变时,评分还是不变,于是导致成绩和评分的相关性太弱,如下图:
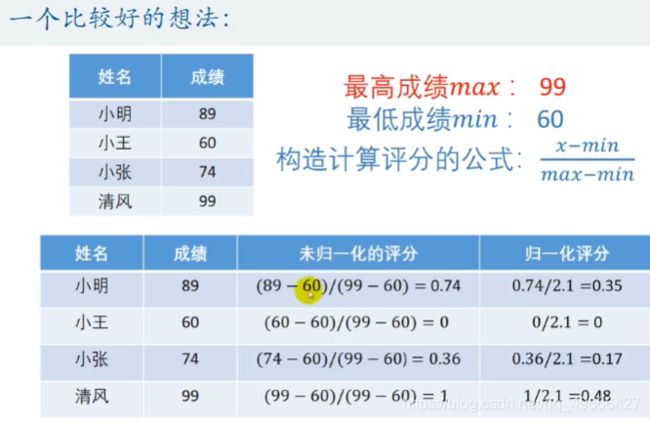
于是想到,对模型进行优化,使评分与成绩的相关性增强,如下图:
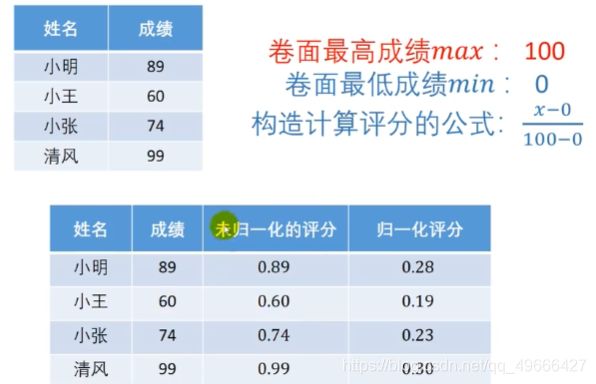
可是,上面的方法在归一化的时候含有0,表示没有分数,但是**事实上最后一名也是有分数的呀!**于是有了下面的一种想法:
这个时候,评分与成绩的数据相关性更加强了,最后一名的评分大于0,说明是有分数的,似乎比上面一种优化更加好,
然而,在很多时候,许多的数据是没有上下限的,例如投资额、GDP增速什么的……(这是最重要的一点!)
而且,最终评分的指标在实际中常常是多个的,而不是只有一个“成绩”,还有其他的指标可能可以起到力挽狂饭的作用,一个小小的0对其影响不大。
更何况,在实际的分析中,常常有许多的数据,在归一化之前,用第二种方法只会影响最大值和最小值这两个对象,当数据比较多的时候,影响较小;
多个指标
指标的类型
一般来说,指标有四种
- 极大型指标(越大越好)
- 极小型指标(越小越好)
- 中间型指标
- 取间型指标
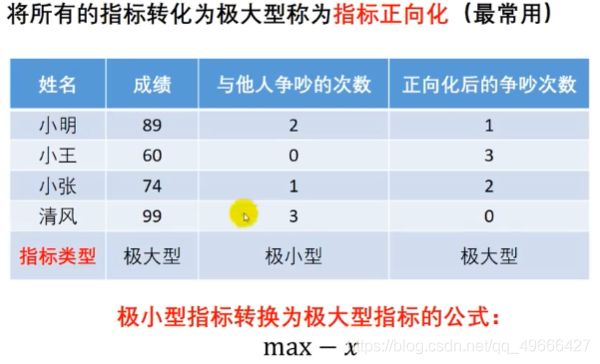
多个不同类型的指标存在时,我们一般都是把极小值指标转化成极大值指标:
专业的说法是:指标正向化
x = max - x;
成功正向化了极小型,那么对于中间型和区间型该怎么正向化呢?
- 对于中间型:
M就是某一项和最佳值的差的最大值,而不是最大值和最小值的差!!
- 对于区间型:(例如人的体温)
- 当落在区间之内的时候,就是1
- 当落在区间之外的时候,就找它到边界的距离
特别注意,显然会有小于下界和大于上界两种情况,但是要注意M的取值是:两个情况的最大值,也就是说,在对超出上界的数据进行正向化的时候,不一定是用某个比较大的数据与上界的差的最大值(如果某个比较小的数据与下界的差比较大数据与上界的差的最大值要大,那就用下界的那个最大差)
指标的量纲
指标正向化之后,由于成绩的单位是分,争吵的次数单位是次
两者根本不是同一类东西把!
那在进行综合评价的时候,我们要对已经正向化的矩阵进行标准化处理消去他们的量纲
标准化处理的计算公式:
咋理解呢?
不就是某个方向的投影/模长吗?
如果是在二维向量中,那不就是我们初中就学过的投影相关的角度吗?cos值那些。
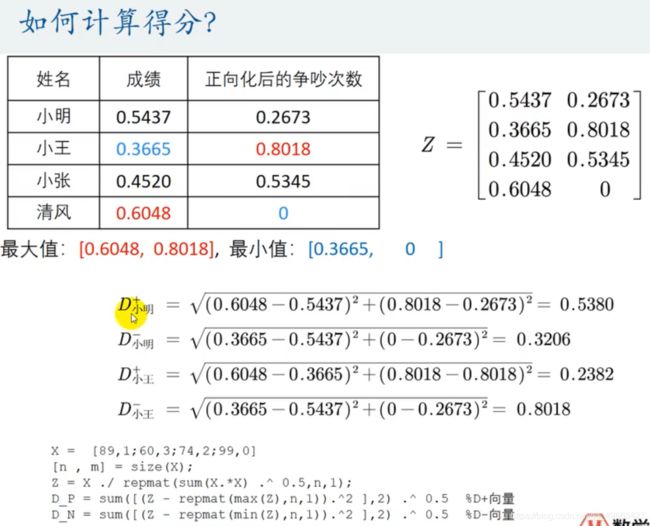
根据指标计算得分
当只有一个指标的时候,即矩阵只有一列,这个时候,计算距离只要减一减就OK了,就相当于是一个数轴嘛,或者说就是一个单一的x轴,然而当有两个指标的时候,就可以看作有x和y轴,这个时候,每一个指标代表一个数轴,于是距离就变成了平方和之后开平方(这里挺自然的吧)
当有多个(多于2个)指标的时候,就相当于有好多好多的轴,于是同样非常自然的想到向量的模
这里比较好的理解方法是:
(对于同一行,先各个指标求差,再求平方、开根号)
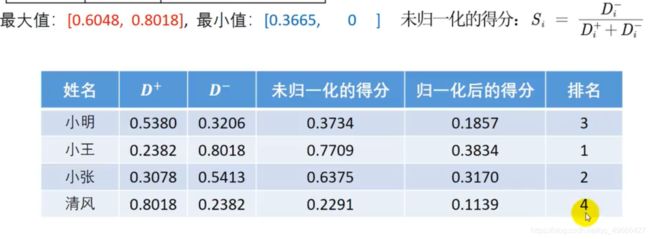
得到的是未归一化的得分,和前面单指标一样,本质都是右上角那一串红色字!!!
- 要计算某一行的得分,先看某一行的各个指标
- 每一个指标都有最大值和最小值,当前行的该指标和当前指标中的最大值与最小值之间的差就相当于 “这个维度的距离” , 就好比在x轴上的某两点坐标差,
- 后一个指标用同样的方法求差就相当于得到y轴上两点距离只差……多维度就相当于多个互相垂直的坐标轴,他们的平方和开根号之后得到欧氏距离
代码实现:
- 数据的载入:
在工作区新建一个矩阵,把excel中的数据粘贴进来。如果以后不想每次用到都复制粘贴一次的话,就可以把这个矩阵另存为.mat后缀的文件,当代码(.m)和数据(.mat)在同一个目录下,就可以用load XXX.mat进行装载
- 指标正向化:
- 极小型指标:
function [posit_x] = Min2Max(x)
posit_x = max(x) - x; %正向化
end
- 中间型指标:
function [posit_x] = Mid2Max(x, best)
M = max(abs(x - best)); %得到最大偏移值作为分母
posit_x = 1 - abs(x - best) / M; %正向化
end
- 区间型指标:
function [posit_x] = Inter2Max(x,a,b)
r_x = size(x,1); %得到列向量的行数
M = max([a - min(x)], max(x) - b); %找到最大的偏移量
posit_x = zeros(r_x , 1); %初始化posit_x全为0
% 为什么这里要把posit_x初始化?前面两个正向化都没有初始化呀?
% 是因为之前都是矩阵的运算,结果肯定是维数相同的;而下面是对每一个元素处理的,没有提前树立好全局的观念,因此要初始化(吗?)
for i = 1 : r_x %遍历
if x(i) < a %小于下界
posit_x(i) = 1 - (a - x(i)) / M;
elseif x(i) > b %大于上界
posit_x(i) = 1 - (x(i) - b) / M;
else %上下界之间
posit_x(i) = 1;
end
end
end
把以上三个类型的正向化函数封装在一个大的正向化函数Positivization中:
function [posit_x] = Positivization(x,type,i)
if type == 1 %极小型
disp(['第' num2str(i) '列是极小型,正在正向化']);
posit_x = Min2Max(x); %调用Min2Max函数来正向化
disp(['第' num2str(i) '列极小型正向化处理完成']);
disp('~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~');
elseif type == 2 %中间型
disp(['第' num2str(i) '列是中间型']);
best = input('请输入最佳的那一个值: ');
posit_x = Mid2Max(x,best);
disp(['第' num2str(i) '列极小型正向化处理完成']);
disp('~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~');
elseif type == 3 %区间型
disp(['第' num2str(i) '列是区间型']);
a = input('请输入区间的下界: ');
b = input('请输入区间的上界: ');
posit_x = Inter2Max(x,a,b);
disp(['第' num2str(i) '列取间型正向化处理完成']);
disp('~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~');
else
disp('没有这种类型的指标,请检查Type向量中是否除了1、2、3之外的其他值');
end
end
%输入变量有三个:
%x:需要正向化处理的指标对应的原始列向量
%type:指标的类型(1:极小型,2:中间型,3:区间型)
- 对每一项指标进行标准化,即去量纲
% 第三步:对正向化后的矩阵进行标准化
Z = X./ repmat(sum(X.*X).^0.5,n ,1)
disp('标准化矩阵');
disp(Z);
- 计算最大值距离和最小值距离,根据公式算出得分,并进行归一化处理
%第四步:计算最大值的距离和最小值的距离,并算出得分
D_P = sum([(Z - repmat(max(Z),n,1)).^2],2).^0.5;%D+ 与最大值的距离向量;
D_N = sum([(Z - repmat(min(Z),n,1)).^2],2).^0.5;%D- 与最小值的距离向量;
S = D_N./(D_P+D_N); %根据公式计算得分
disp('最后的得分为:');
stand_S = S/sum(S); %归一化处理
[sorted_S,index] = sort(stand_S,'descend'); %降序排列,结果存在sorted_S变量中,并带有索引index