因果推断1
相关性并不意味着因果关系” 这个道理对大家都不陌生。 我们如何科学、优雅地做一份关于 “因果关系” 数据分析呢? 在这篇文章里,我们从因果推断对于数据分析的重要性出发,和大家分享一个因果推断的经典框架、一组因果推断的必备假设和一个因果推断的基础方法。
WHY:为什么需要因果推断
“相关性并不意味着因果关系”,天天和数据打交道的小伙伴们都很明白这个道理。 不少数据分析的工作其实都围绕着这个问题,举一些例子:
- 在 feeds 流里刷到一个新推荐策略的内容的用户留存更高,他们的高留存是因为这个推荐策略导致的吗,这个策略究竟对留存的提升有多大效果?
- 上周投放了某游戏广告的用户登录率更高,他们的高登录率有多大程度是由广告带来的,有多大程度是由于他们本身就是高潜力用户?
- ……
在这些例子中,本质上,我们都是想要分析一个干预(treatment)对一个结果(outcome)有怎样的影响,想要探究其中的因果效应。大家熟悉的 A/B Test 是回答上面这些问题的黄金方式。但是,A/B Test 也有一定的局限性,例如:
- 需要花一定的时间实现,比较耗费人力;
- 需要占用足量的随机流量,并且需要持续一段时间以收集数据;
- 某些实验可能损害用户体验,例如给用户推荐一些并不匹配兴趣的内容;
- 当可做 A/B Test 的选择太多时,往往难以全部都进行尝试。
鉴于 A/B Test 的种种局限性,研究如何利用手边已有的历史数据进行 “因果分析” 变得无比重要。
WHAT:因果推断推什么
因果推断用的最多的模型有两个。一个是著名的统计学家 Donald Rubin 教授在 1978 年提出的 “潜在结果模型”(potential outcome framework),也称为 Rubin Causal Model(RCM)。另一个是 Judea Pearl 教授在 1995 年提出的因果图模型(Causal Diagram)。这两个模型实际上是等价的。从数据分析角度而言,个人认为潜在结果模型的数学描述更加严谨,这篇文章也使用潜在结果模型来给出因果推断的定义。
首先,我们需要定义一些符号。
- 干预 (treatment)
:一般我们考虑二值干预,用 ∈0,1 来指示用户是否受到了某种干预,例如是否被投放了某广告、是否被灰度了某功能。在 A/B Test 中,实验组的用户都受到了某种处理,他们都有 =1
- 。
- 潜在结果(potential outcome){0,1}
- :对每个用户 ,他们对于是否受到干预分别有两个潜在结果 0 和 1。例如,0 和 1
- 分别表示假如一个用户没有被投放游戏广告和被投放时是否会登录游戏。
- 观察结果(observed outcome)
- :当一个用户没有受到干预时(=0),我们将会观察到 =0,当一个用户受到干预时我们将会观察到 =1
- 。
在因果分析中,我们通常比较关心以下两种 “因果效应”。为了符号简洁,接下来不再特意标注出代表用户的下标
。
- 平均因果效应 (Average Treatment Effect,简称 ATE): =[1−0]
- 。ATE 为干预对所有人的平均因果效应。
- 干预组的而平均因果效应(Average Treatment Effect on the Treated,简称 ATT):=[1−0|=1]
- 。ATT 为干预对受到干预的人的平均因果效应。
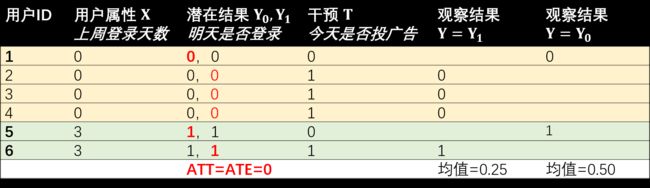
以游戏广告投放为例,我们举一个例子如下表,这个例子接下来还会反复使用。假如我们可以同时观测到两个潜在结果(尽管这是不可能的),我们可以算出 =(0+0+0+0+0+0)/6=0
,=(0+0+0+0)/4=0
。
当我们尝试直接从观察结果
统计 ATE 或者 ATT 时,我们就会遇到一个问题:对于每一个用户,我们并不能同时观测到两个潜在结果。这个问题是因果推断的一个核心问题、核心难点。
A/B Test 提供了解决这个核心问题的完美方案,让我们通过简单的公式看看为什么。在做 A/B Test 时,我们一般直接统计实验组和对照组的指标差异。严谨来说,我们的估算方式为 ^=[1│=1]−[0|=0]
。根据 ATT 的定义,我们可以得到如下公式推导 =[1−0│=1]=([1│=1]−[0│=0])+([0│=1]−[0│=0])=^+。这里的 bias,根据定义来看,是实验组和对照组的潜在结果 0 的差异。在 A/B Test 中,我们假设实验组和对照组是随机划分的,因此 bias 为 0。因此,根据 A/B Test 计算的 ^
就是 ATT 的无偏估计。
在日常工作中,并非所有数据分析都有 A/B Test 撑腰。我们往往需要通过观察历史数据完成分析,这类分析称为 “观察性研究”。在观察性研究中,失去了 “随机流量” 的撑腰,现实就没有那么美好了。这时,如果我们直接比较两组用户指标上的差异得到 ^
,它和真实的 ATT 之间是存在一个非零的 bias 的,我们无法根据 ^ 下一个科学可靠的结论。 例如,在之前使用的广告投放的例子中,假设我们直接比较 =1 和 =0 两组用户的观测结果
的差异,会造成投放广告造成登录率从 50% 下跌到 25% 的错觉,这并不是真实的 ATE 和 ATT。
WHEN:因果效应的可识别性
在观察性研究中,借助什么样的数据可以推出可靠的因果效应(ATE 或 ATT)呢?具体来说,假如我们对每个用户有一系列干预前的指标(pre-treatment variables)
、有干预 、有观察结果
,我们能不能推断出 T 对 Y 的因果效应?
这个问题就是因果推断的可识别性(identifiability)问题。可识别性依赖于几个假设,这些假设通常被称为 causal assumption。下面我们一个一个来看看。
Stable Unit Treatment Value Assumption (SUTVA)
SUTVA 假设用户之间是相互独立的,无互相干扰。SUTVA 保证个体的潜在结果只和他自己有关、最终观察到的结果也只和他自己有关。值得注意的是,社交网络上的实验理论上都很难完完全全保证 SUTVA,但是对于大部分社交属性不强的实验,一般还是假设 SUTVA 基本成立。
Ignorability
Ignorability 假设对于 pre-treatment 变量
一样的人群,是否接受处理和潜在结果相互独立:0,1⊥|
。
这个假设比较难以理解,我们套用之前举的广告投放的例子看看。在这个例子中,我们倾向于给历史登录天数少的用户投放广告,
和 是负相关的。同时,历史登录天数越多,未来登录率也越高,即 X 和潜在结果 0 和 1 都是正相关的。在这份数据里,(0,1) 和 并不独立。但是,对于
取值一样的用户,是否看到广告可以看做是随机的,ignorability 成立。
Ignorability 这个假设还有很多其它的名字,例如 no unmeasured confounders assumption 和 Conditional Independence Assumption (CIA)。
Consistency
Consistency 假设潜在结果和观察到的结果是一致的,即当 =
时 =
。这个假设一般可以认为是成立的。
Positivity
Positivity 假设要求 treatment assignment 有一定随机性,要求对于
的所有取值都有 0<[=1|=]<1
。如果这个假设不成立,我们是无法下结论的。例如当一部分用户不可能被投放广告时,我们无法通过历史数据分析广告对他们的效果。当 positivity 假设不成立时,我们往往需要考虑去除一些特殊用户群。
Positivity 这个假设也有些其它的名字,常见的有 common support 和 overlap。
A/B Test 满足上面的每一个假设,有心的小伙伴可以花 3 分钟在内心默默确认一下,这里就不多唠叨了。
在观察性研究中,SUTVA、ignorability 和 consistency 这三个假设都是无法验证的(untestable)。有时我们可以通过一些经验或是数据判断出这些假设明显不成立,但是我们没有办法可以证明这些假设成立。
HOW:因果推断的基础方式
假设我们有一份数据,我们判断几个 causal assumption 都是成立的,我们应该如何推断其中的因果效应呢?基于潜在结果模型,一套比较经典的因果效应推断方式是 Matching。Matching 这个方法从名字来看很直观,但是里头还是有一些套路的。
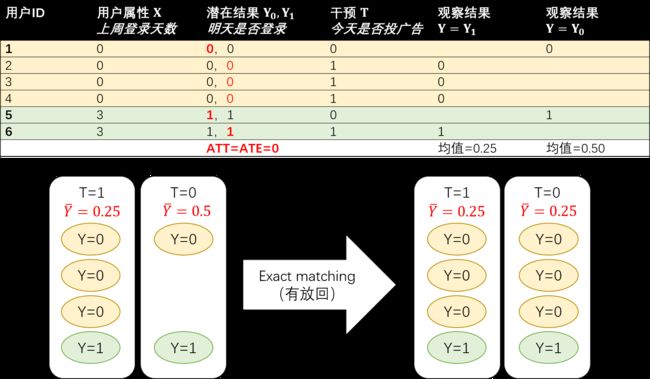
最最基本款的 Matching 是 Exact Matching。假设我们感兴趣的因果效应是 ATT,我们需要做的事很简单,对于每一个 =1
的用户,我们从 =0 的分组里找一个 pre-treatment 变量 一模一样的用户,把他们配成对,找不到就放弃。配对过程结束后,一部分或者全部 =1 的用户找到了平行世界的自己,我们直接比较两组用户观察结果
的差异就可以得到结论。 继续使用之前提到的广告投放的例子,假设我们进行一个有放回的 Exact Matching,配对结果如下。估算的 ATT 为 0。
Exact Matching 虽然直观,但是并不实用。“匹配用户的变量
完全相等” 这个要求过于严格,随着变量
的维度的增加,几乎不太可能有足量的匹配用户来下结论。
Exact Matching 的一个直观变种是 Distance Matching。我们可以对每一个 =1
的用户匹配一个距离最近并且不超过阈值的用户。这里 “距离” 如何定义、“阈值” 如何定义,也都需要更多的斟酌。另外,当我们通过距离来匹配时,其实是在潜意识里假设了变量 X 的每一个维度都是同等 “重要” 的,这里也不一定科学。
为了科学有效地进行 Matching,一个经典的做法是 Propensity Score Matching,简称 PSM。在 PSM 方法中,我们首先对每一个用户计算一个倾向性得分(propensity score),定义为 ()=(=1|=)
。接着我们根据倾向性得分将用户进行匹配 ,从而得到两个
上看起来基本同质的用户组,然后统计得到 ATT。PSM 方法在实现上有许多值得深入介绍的地方,例如如何得到 “倾向性得分”、如何选择匹配方式(如一对一匹配、一对多匹配、分层匹配、有放回或无放回匹配)、如何衡量匹配质量等。关于更多 PSM 的细节,将会在下一篇文章里深入介绍。等不及的小伙伴也可以读一读参考资料中的 [6]。
小结
在这篇文章里,我们通过 “潜在因果模型” 进入了因果推断的世界,介绍了因果推断的几个必备假设,分享了一个因果推断的基础方法。希望起抛砖引玉的作用,让更多小伙伴了解到因果推断,引发大家更多的思考和讨论。
参考资料
- [科普文] 统计之都的因果推断系列系列,出自 UC Berkeley 的丁鹏教授(师从 Doanald Rubin)
- [公开课] A Crash Course in Causality: Inferring Causal Effects from Observational Data (Prof. Jason A. Roy, Ph.D., UPenn)
- [教材] Causal Inference for Statistics, Social, and Biomedical. Sciences: An Introduction. Guido W. Imbens and. Donald B. Rubin.
- [教材] Causality: Models, Reasoning and Inference. Judea Pearl.
- [工业界 paper] Gordon, B. R., Zettelmeyer, F., Bhargava, N., & Chapsky, D. (2017). A Comparison of Approaches to Advertising Measurement: Evidence from Big Field Experiments at Facebook. Ssrn. https://doi.org/10.2139/ssrn.3033144
- [综述类 paper] Caliendo M, Kopeinig S. Some practical guidance for the implementation of propensity score matching[J]. Journal of economic surveys, 2008, 22(1): 31-72.