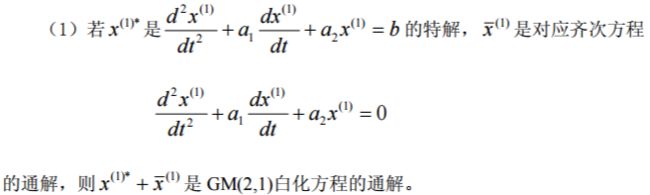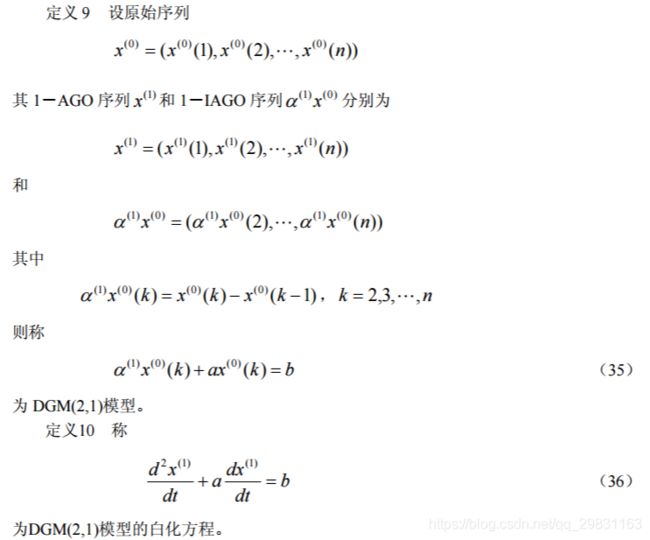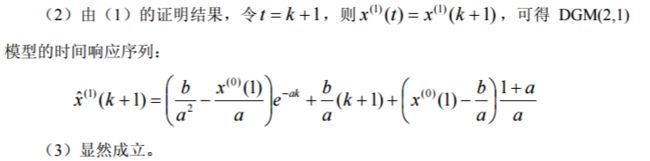灰色系统理论及其应用 (八) ：GM(2,1)和 DGM 模型

---

灰色系统理论及其应用系列博文：

灰色系统理论及其应用 (一) ：灰色系统概论、关联分析、与传统统计方法的比较

灰色系统理论及其应用 (二) ：优势分析

灰色系统理论及其应用 (三) ：生成数

灰色系统理论及其应用 (四) ：灰色模型 GM

灰色系统理论及其应用 (五) ：灰色预测

灰色系统理论及其应用 (六) ：SARS 疫情对某些经济指标影响问题

灰色系统理论及其应用 (七) ：道路交通事故灰色 Verhulst 预测模型

灰色系统理论及其应用 (八) ：GM(2,1)和 DGM 模型

灰色系统理论及其应用 (九) ： GM(1, N) 和GM(0, N) 模型

---

GM(1,1)模型适用于具有较强指数规律的序列，只能描述单调的变化过程，对于非单调的摆动发展序列或有饱和的 S 形序列，可以考虑建立 GM(2,1)，DGM 和 Verhulst 模型。

---

目录

1 GM(2,1)模型                             （2）齐次方程的通解有以下三种情况：

2    DGM(2,1)模型                             例6    试对序列建模DGM(2,1)

---

1 GM(2,1)模型

（2）齐次方程的通解有以下三种情况：

（3）白化方程的特解有以下三种情况：

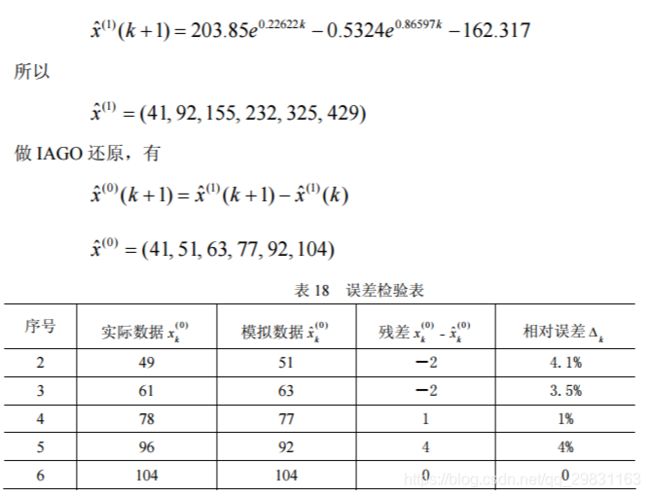
 例 5 上海市上网户数的 GM(2,1)模型。1996～2001 年上海市上网户数数据序列为

计算的 MATLAB 程序如下：

clc,clear
x0=[41,49,61,78,96,104];
n=length(x0);
x1=cumsum(x0)
a_x0=diff(x0);
a_x0=[0,a_x0]
for i=2:n
    z(i)=0.5*(x1(i)+x1(i-1));
end
B=[-x0(2:end)',-z(2:end)',ones(n-1,1)];
Y=a_x0(2:end)';
u=B\Y
x=dsolve('D2x+a1*Dx+a2*x=b','x(0)=c1,x(5)=c2');
x=subs(x,{'a1','a2','b','c1','c2'},{u(1),u(2),u(3),x1(1),x1(6)});
yuce=subs(x,'t',0:n-1);
digits(6),x=vpa(x)
x0_hat=[yuce(1),diff(yuce)]
epsilon=x0-x0_hat
delta=abs(epsilon./x0)

2    DGM(2,1)模型

例6    试对序列建模DGM(2,1)

计算的MATLAB程序如下：

clc,clear
x0=[2.874,3.278,3.39,3.679,3.77,3.8];
n=length(x0);
a_x0=diff(x0);
a_x0=[0,a_x0]
B=[-x0(2:end)',ones(n-1,1)];
Y=a_x0(2:end)';
u=B\Y
x=dsolve('D2x+a*Dx=b','x(0)=c1,Dx(0)=c2');
x=subs(x,{'a','b','c1','c2'},{u(1),u(2),x0(1),x0(1)});
yuce=subs(x,'t',0:n-1);
digits(6),x=vpa(x)
x0_hat=[yuce(1),diff(yuce)]
epsilon=x0-x0_hat
delta=abs(epsilon./x0)

---

灰色系统理论及其应用系列博文：

灰色系统理论及其应用 (一) ：灰色系统概论、关联分析、与传统统计方法的比较

灰色系统理论及其应用 (二) ：优势分析

灰色系统理论及其应用 (三) ：生成数

灰色系统理论及其应用 (四) ：灰色模型 GM

灰色系统理论及其应用 (五) ：灰色预测

灰色系统理论及其应用 (六) ：SARS 疫情对某些经济指标影响问题

灰色系统理论及其应用 (七) ：道路交通事故灰色 Verhulst 预测模型

灰色系统理论及其应用 (八) ：GM(2,1)和 DGM 模型

灰色系统理论及其应用 (九) ： GM(1, N) 和GM(0, N) 模型

---