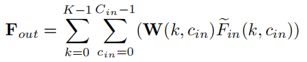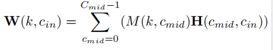PointConv解读

PointConv：Deep Convolutional Networks on 3D Point Clouds

摘要

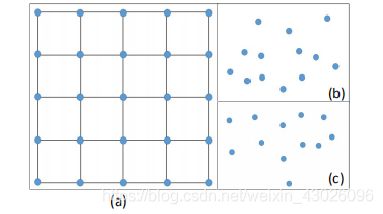
传统的卷积是作用在二维图像数据上，图像数据通常可以表示成密集的网格形式。在CNN中，每个滤波器被限制在一个小的局部区域内，例如3×3；5×5等。在每个局部区域内，不同像素之间的相对位置总是固定的，如图（a）所示。

三维数据通常是以点云的形式表示，就是一组无序的三维点，一组点云集合可以表示为一组3D点的集合{p_i|i=1，…，n}，其中每个点包含一组位置向量(x,y,z)或其它信息如颜色、表面切线等。不同于图像，点云的表示形式更灵活。在坐标系p=(x,y,z)∈R^3中，一个点的坐标不会限制在一个固定网格里，而是有可能取任意的连续值（如图（b）和（c）所示）。因此，一个点云在不同的局部区域内的顺序和相对位置都是不同的。栅格化的图像上的传统离散卷积滤波器不能直接应用于点云，因此，在点云数据上使用卷积是困难的。

相关工作

3D CNN网络上的大多数工作都将3D点云转换为2D图像或3D体积网格，然后应用2D、3D卷积网络进行处理。最新的有将点云直接作为输入处理的工作，例如：

(1) PointNet：Deep Learning on Point Sets for 3D Classification and Segmentation

首先独立地处理每个点进行一定程度的特征提取，然后利用最大池化得到一个全局特征，但是使用最大池化可能会丢失一些有用的细节信息并且PointNet没有利用数据局部的相关性。

(2) PointNet++：Deep Hierarchical Feature Learning on Point Sets in a Metric Space

在PointNet基础上添加了分层抽取特征的想法，每个图层都有三个子阶段：采样层，组合层和特征提取层，不同尺度提取局部特征，通过多层网络结构得到深层特征。解决了点云密度不同的问题，但是计算量过大并且使用最大池化可能会丢失一些有用的细节信息。

(3) PointCNN：Convolution On X -Transformed Points

提出了根据输入点学习一种X变换，然后将其用它来同时对点关联的输入特征进行加权和置换。但是无法实现排列不变性。

本文使用点云作为输入，通过学习一个MLP来估计权重函数，然后通过在权重上应用反转密度缩放来补偿非均匀采样造成的影响。由于PointConv是卷积的完全近似，因此由PointConv可以很方便的得到PointDeconv，使用它可以提高点云分割任务的性能。

PointConv

在3D空间中，可以把连续卷积算子的权重看作是关于一个3D参考点的局部坐标的连续函数：

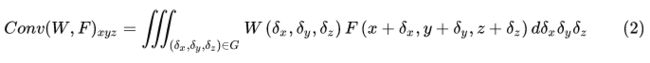
其中W和F均为连续函数，F是以点p(x,y,z)为中心的局部区域G中点的特征。一组点云可以视为从一个连续空间R^3进行非均匀采样的结果。在每个局部区域中，(δx, δy, δz)可能是局部区域的任何可能的位置，上式可以离散化到一个离散的3D点云上：

S(δx, δy, δz) 是点(δx, δy, δz)处的逆密度估计，然后使用逆密度估计对学到的权重进行加权，补偿不均匀采样。
假设一共有8000个点，使用kernel_density_estimation_ball 求每个点的密度，得到（8000,1）的密度特征，对这个密度进行非线性处理（输入一个mlp中），让这个特征变得可学习。然后把这个密度求逆，作为权重。就是上面公式里的S。

PointConv

原始的PointConv：

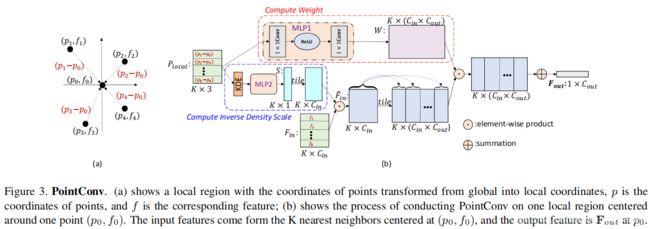
（a）显示了一个局部区域，其点的坐标已从全局坐标转换为局部坐标，p是点的坐标，f是相应的特征.
（b）显示了在以一个点(p_0,f_0)为中心的一个局部区域上执行PointConv的过程。

红框部分：估计权重函数W。
篮框部分：估计反密度函数S。

原生PointConv运算步骤：
① 给定输入点p，通过K近邻得到局部区域中的k个点，输入为3D局部位置坐标信息，记为P_local ∈ R^(K×3)，P_local通过减去局部区域的质心的坐标来计算。
②通过核密度估计（KDE）计算反密度，然后通过MLP2进行映射等到S，对S进行复制平铺，最后得到大小为K × C_in 的反密度张量。
③把②和输入特征F_in（K × C_in）进行点乘运算，输出大小为K × C_in，再经过复制平铺，最后得到大小为K × (C_in × C_out)的中间张量(F_in)~
④把P_local的k个点坐标输入MLP1，输出大小为K × (C_in × C_out)的权重张量。
⑤把③和④进行点乘运算，输出大小为K × (C_in × C_out)的张量，最后求和得到下式F_out。

使用KDE(核密度估计)的方法计算每个临近点的密度,KDE算的密度是密度越大地方值越大，所以我们这边需要使用的是密度的倒数，把密度的倒数送进MLP2中最终得到逆密度S，并将临近点的密度S复制了Cin次，将密度与Fin进行相乘，这样就达到了通过密度来干预特征权重的作用。

高效的PointConv：

但是，由于原始的PointConv内存消耗巨大并且效率低下，本文作者提出了一种新的重构方法，这种方法通过将原始的PointConv减少到两个标准操作来实现：矩阵乘法和2d卷积。

因为反密度估计函数不存在内存问题，所以下面的讨论主要集中在权重函数上。

将训练阶段的mini-batch size记为B，点云中的点的个数记为N，每个点的邻域中点的个数记为K，C_in为输入点的通道数，C_out为点的输出通道通道数。对一个点云而言，每部分局部区域都共享从MLP习得的相同的权重函数。但是对不同位置的不同点而言，运算得到的权重应当是不同的。由MLP生成的权重卷积核参数大小约为B × N × K × (C_in × C_out)。为此，本文提出高效版PointConv。

即高效的PointConv是将卷积核分为两部分：中间结果M（权重函数的MLP中最后一层的输入）和卷积核H（同一MLP中最后一层的权重）。

权重表示为：

代入之前的F_out得到最终的F_out为：

内存大小变为:B×N×C_mid×C_in，内存开销为原始PointConv的C_mid/(K*C_out)倍。

PointDeconv

对于语义分割任务，需要逐点预测。为了获得所有输入点的特征，需要一种将特征从二次采样点云传播到更密集的点的方法。本文提出添加一个基于PointConv的PointDeconv层作为反卷积操作来解决这个问题，充分利用反卷积操作来捕获来自粗粒度级别的局部相关信息。

如图4所示，PointDeconv由两部分组成：插值和PointConv。首先，我们使用插值来传播前一层的粗粒度特征，通过从3个最近点来进行线性特征插值。然后，使用skip links将插值特征与来自卷积层的具有相同分辨率的特征连接起来。连接后，我们在连接的特征上应用PointConv以获得最终的反卷积输出。我们反复执行此过程，直到所有输入点的要素已传播回原始分辨率。

实验结果
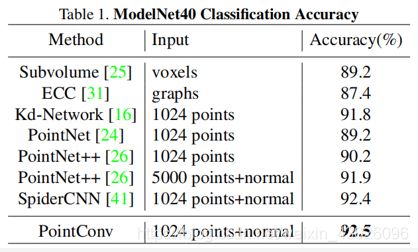
1、ModelNet40分类任务

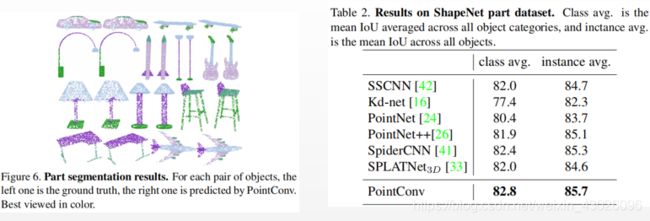
2、ShapeNet 零件分割
任务的输入是由点云表示的形状，目标是为点云中的每个点分配零件类别标签。 给出了每种形状的类别标签。 通常，通过使用已知的输入3D对象类别将可能的零件标签缩小到特定于给定对象类别的部分标签。 并且还将每个点的法线方向计算为输入特征，以更好地描述基础形状。

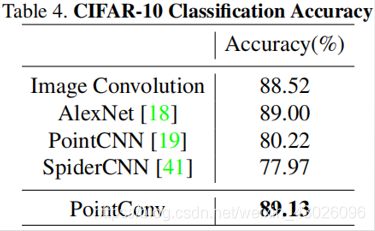
3、CIFAR-10分类结果
作者使用CIFAR-10数据集验证PointConv和2D CNN有相同的学习能力，将CIFAR-10中的每个像素都视为具有xy坐标和RGB特征的2D点。 在训练和测试之前，将点云缩放到单位球上。

4、场景语义标注
由于ModelNet40和ShapeNet数据集都是人为合成的数据集，大多数最先进的算法都能在此类数据集上取得不错的效果，故我们使用ScanNet数据集（包含大量噪声数据的真实点云）评估PointConv。任务是在给定由点云表示的室内场景的情况下，预测每个3D点上的语义对象标签。

5、消融研究
作者在ScanNet数据集上对MLP结构和逆密度标度等进行消融研究，测试PointConv的性能。

结论
本文中，我们提出了一种新的方法来对3D点云进行卷积运算，称为PointConv。PointConv训练局部点坐标上的多层感知器，从而近似卷积核中的连续权重和密度函数，这种方法使得它自然地具备序列不变性和平移不变性。使用该卷积，可以直接在3D点云上构建深度卷积网络。并且提出了一种有效的实现方法，大大提高了它的可扩展性。

主要贡献：
（1）提出PointConv，一种密度函数重加权卷积，它能够在任何3D点集上完全逼近3D连续卷积。
目前所有的基于点云上的算法，第一步做的都是最远点采样（FPS） ，从宏观上来看，最远点采样的方法在减少点云样本数量的同时也极大的保留点云的原始的空间结构。但是从微观上看，最远点采样的算法属于非均匀采样，这样就会导致某些局部区域点大量聚集，而某些区域的的点的数量只有寥寥无几。而PointConv正是发现这一问题，尝试着通过核密度估计方法来解决这个问题。

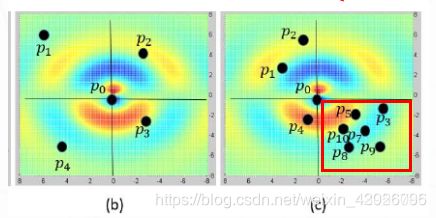
对于上图，我们尽可能的希望通过最远点采样得到的采样的点分布是（b)的情况，采样点近似于均匀分布。但是绝大部分的时候，我们的采样点的分布更接近于（c），这也更接近真实的情况。但是我们从（c) 中很轻而易举的想到一个例子作者为什么要使用核密度估计啦。
**例子：**假设图©中的点，红色方框里面的点是代表桌面上的点。而p1,p2则代表的是桌角上的点的。那我们可以很容易的知道，当我们的网络要知道哪个区域是代表桌面，那么则会有七八个点告诉我们的网络该区域是桌面，而当我们的网络想知道桌角是哪个区域的时候，只有一到两个点可以告知它。当网络在提取特征的时候，如果失去了这两个点的特征，那我们的网络就将永远失去了对该场景桌面特征的提取，但是对于桌面特征的提取，即使我们的网络丢失了好几点，但是最终还是有点可以告诉我们网络，该区域是桌面。理所当然，如果我们能有意的提高p1,p2这两个代表桌角点的权重，让我们的网络重视这个两个点，这样就不至于网络会丢失这两个点的特征。理所当然我们也要降低点密度较大的地方的权重。

（2）设计了一种内存高效的方法来实现PointConv，即通过求和顺序技术的变化提升性能。
（3）将PointConv扩展为反卷积（PointDeconv）版本以获得更好的分割结果。