SLAM学习笔记(二)
第五讲.相机与图像
相机将三维世界中的坐标点(单位米)映射到二维图像平面(单位为像素)的过程中能够用一个几何模型进行描述。
单目相机(Mono)的成像过程:
1、世界坐标系下有个固定的点P,世界坐标为![]()
2、由于相机在运动,它的运动由![]() 或变换矩阵
或变换矩阵![]() 描述。P的相机坐标为
描述。P的相机坐标为![]()
3、这时的![]() 的分量为X,Y,Z,把他们投影到归一化平面Z=1上,得到P的归一化坐标:
的分量为X,Y,Z,把他们投影到归一化平面Z=1上,得到P的归一化坐标:![]()
4、有畸变时,根据畸变参数计算![]() 发生畸变后的坐标。
发生畸变后的坐标。
5、P的归一化坐标经过内参后,对应到它的像素坐标:![]()
双目相机模型:
双目相机原理:通过同步采集左右相机的图像,计算图像间视差,以便估计每一个像素的深度。
基线:两个光圈中心的距离。
根据视差可以估计一个像素与相机之间的距离。视差与距离成反比:视差越大,距离越近。
视差本身很难计算。而且只有在图像纹理变化丰富的地方才能计算视差。由于计算量的原因,双目深度估计仍需要使用GPU或者FPGA来实时计算。
RGB-D相机模型:
它能够主动测量每个像素的深度。目前的RGB-D相机按原理可分为两大类:
1、通过红外结构光(Structured Light)原理测量像素距离。
2、通过飞行时间(Time-of-Flight, ToF)原理测量像素距离。
RGB-D相机能够实时地测量每个像素的距离。但是使用范围受限。使用红外光进行深度测量的RGB-D相机,任意受到日光或者其他传感器发射的红外光干扰,因此不能在室外使用。在没有调制的情况下,同时使用多个RGB-D相机时也会相互干扰。对于投射材质的物体,因为接收不到反射光,所以无法测量这些点的位置。成本和功耗也较高。
图像
在数学中,图像可以用一个矩阵来描述,计算机中它们占据 一段连续的磁盘或内存空间,可以用二维数组表示。
在一张灰度图中,每个像素位置![]() 对应一个灰度值
对应一个灰度值![]() ,一张宽度为w、高度为h的图像数学上可以记为一个函数:
,一张宽度为w、高度为h的图像数学上可以记为一个函数:
![]()
灰度图中像素的取值范围 (0-255),一个字节就够了。一张宽度为640像素、高度480像素分辨率的灰度图可以表示为:
unsigned char image[480][640]图像以二维数组形式存储,第一个下标指数组的行,第二个下标指数组的列。在图像中,行数对应图像的高度,列数对应图像的宽度。
像素坐标系原点位于图像的左上角,X轴向右,Y轴向下。如果有第三个轴---Z轴,根据右手法则Z轴应该是向前的。
彩色图像:R\G\B三通道(channel)每个通道都由8位整数表示,一个像素占据24位空间。通道的数量和顺序都可以自定义。在OpenCV的彩色图像中,通道的默认顺序是B、G、R。一个24位的像素,前八位表示蓝色数值,中间八位表示绿色数值,最后8位表示红色数值。如果还想表达图像的透明度,就使用R、G、B、A四个通道。
第六讲、非线性优化
经典slam模型可由运动方程和观测方程组成。方程中的位姿可以由变换矩阵来描述,然后用李代数进行优化。观测方程由相机模型给出,其中内参是固定的,而外参是相机的位姿。
由于噪声的存在,运动方程和观测方程的等式必定不是精确成立的。与其假设数据必须复合方程,不如讨论如何在有噪声的数据中进行准确的状态估计。
SLAM 模型:
![]()
![]() 是相机的位姿,可以用SE(3)描述。观测方程即针孔相机模型。
是相机的位姿,可以用SE(3)描述。观测方程即针孔相机模型。
处理状态估计的方法分两种:增量、批量。增量方法只关心当前时刻的状态估计![]() ;批量方法可以在更大的范围达到最优化,被认为由于传统的滤波器,而成为当前SLAM主流方法,但不满足应用场景的是实时性。比较实用的方法是滑动窗口估计法。
;批量方法可以在更大的范围达到最优化,被认为由于传统的滤波器,而成为当前SLAM主流方法,但不满足应用场景的是实时性。比较实用的方法是滑动窗口估计法。
批量法:考虑1到N的所有时刻,并假设有M个路标点。定义所有时刻的机器人位姿和路标点坐标为:
![]()
用u表示所有时刻的输入,z表示所有时刻的观测数据。对机器人状态的估计,从概率学的观点看,就是已知输入数据u和观测数据z的条件下,求状态x,y的条件概率分布:
![]()
特别地,当控制输入未知时,只有一张张的图象时,即只考虑观测方程带来的数据时,相当于估计![]() 的条件概率分布,此问题也称SfM,即如何从许多图像中重建三维空间结构。
的条件概率分布,此问题也称SfM,即如何从许多图像中重建三维空间结构。
利用贝叶斯法则,估计状态变量的条件分布,有
贝叶斯法则左侧称为i后验概率,右侧的![]() 称为似然(Likehood),另一部分
称为似然(Likehood),另一部分![]() 称为先验(Prior) 。求一个状态最优估计,使得在该状态下后验概率最大化:
称为先验(Prior) 。求一个状态最优估计,使得在该状态下后验概率最大化:
![]()
贝叶斯法则分母部分与带估计的状态x,y无关,因此可以忽略。贝叶斯法则告诉我们:
求解最大后验概率等价于最大似然和先验概率的乘积。
机器人位姿或路标未知,此时就没了先验。可求解最大似然估计(Maximize Likehood Estimation,MLE):
![]()
最大似然可以理解成:“在什么样的状态下,最可能产生现在观测到的数据。”
最小二乘法
简单的最小二乘问题:
![]()
求解目标函数导数![]() 。不方便之际求解的最小二乘问题,采用迭代的方式,从一个初始值出发,不断地更新当前的优化变量,使目标函数下降。具体步骤如下:
。不方便之际求解的最小二乘问题,采用迭代的方式,从一个初始值出发,不断地更新当前的优化变量,使目标函数下降。具体步骤如下:
- 给定某初始值

- 对于第k次迭代,寻找一个增量
 ,使得
,使得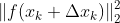 达到最小值。
达到最小值。 - 若
 足够小,则停止。
足够小,则停止。 - 否则,令
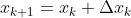 ,返回第二步。
,返回第二步。
这使得求解导函数为零的问题变为一个不断寻找下降增量![]() 的问题。
的问题。
一阶和二阶梯度法
将目标函数在![]() 附近进行泰勒展开:
附近进行泰勒展开:
![]() 是
是![]() 关于x的一阶导数(也叫梯度、雅可比矩阵),
关于x的一阶导数(也叫梯度、雅可比矩阵),![]() 则是二阶导数(海塞矩阵)它们都在
则是二阶导数(海塞矩阵)它们都在![]() 处取值。
处取值。
保留泰勒展开的一阶或二阶项,对应的求解方法则称为一节梯度或二阶梯度法。
如果保留一阶梯度,取增量为反方向的梯度,即可保证函数下降:
![]()
最速下降法:沿着梯度反方向前进,在一阶线性的近似下,目标函数必定下降。
保留二阶梯度信息,此时增量方程:
求右侧等式关于![]() 的导数并令它为零,得到:
的导数并令它为零,得到:
![]()
求解该线性方程,就得到了增量。该方法又称为牛顿法。