科普SLAM之位姿图优化建图
科普SLAM之位姿图优化建图
本讲重点
- 位姿图优化建图的基本定义(什么是PGO ?)
- 位姿图优化建图的研究意义(为什么需要PGO?)
- 位姿图优化建图的基本原理(PGO如何产生的?)
- 位姿图优化建图的算法流程(PGO 如何工作的?)
- 位姿图优化建图的性能改善(如何改善PGO?)
1. 位姿图优化建图的基本定义(什么是PGO ?)
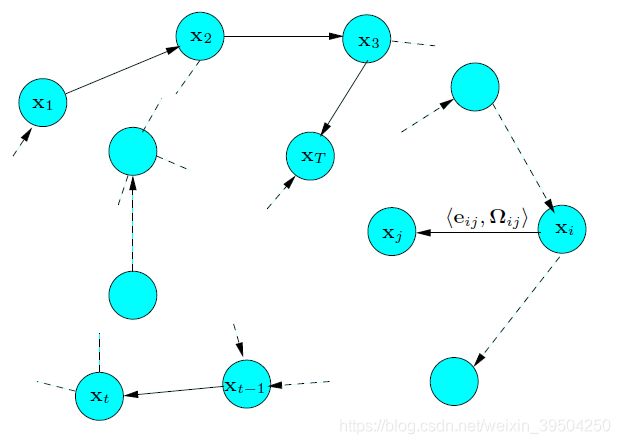
位姿图优化建图(Pose Graph Optimization)是基于最小二乘非线性优化的建图方法;它使用节点-边(Vertex-Edge)位姿图的方式来对于机器人的同时定位建图(SLAM)问题进行建模。通过构造节点-边(Vertex-Edge)位姿图这种模型,来将最小二乘的非线性优化问题,形象地转化成为图优化问题。图【1】描述了位姿图优化的模型特点。其中每个节点 p k \mathbf{p}_k pk代表机器人在时刻 k k k的位姿(位置与朝向),两个节点 p i \mathbf{p}_i pi与 p j \mathbf{p}_j pj之间通过运动约束 e i j \mathbf{e}_{ij} eij来联系;运动约束 e i j \mathbf{e}_{ij} eij描述了这两个节点之间的相对平移 t i j \mathbf{t}_{ij} tij与相对旋转 θ i j \mathbf{\theta}_{ij} θij,相关联的协方差矩阵 Ω i j \Omega_{ij} Ωij描述了运动约束的不确定性的大小。
图【1】位姿图优化的模型
求解的过程,就是找到一组优化的节点系列 p ∗ \mathbf{p}^{*} p∗,使得它们所构建的图,能够与运动约束之间的偏差最小。从数学描述来讲,就是来找到一组优化变量 p ∗ \mathbf{p}^{*} p∗,使得目标函数取得极小值 p ∗ = arg min ∑ ( i , j ) ∥ e i j − R i j T ⋅ ( p j − p i ) ∥ 2 \mathbf{p}^{*} = \arg\min\sum_{(i,j)}\|e_{ij} - \mathbf{R}_{ij}^T \cdot (\mathbf{p}_j - \mathbf{p}_i)\|^2 p∗=argmin∑(i,j)∥eij−RijT⋅(pj−pi)∥2
形象举例来讲,这个节点-运动约束所构建出来的图,就好比通过弹簧所构建出来的网络;其中运动约束,就好比弹簧因为形变所导致的弹力。通过优化过程,使得弹簧之间的形变在合适的状态,从而使得整体的弹簧势能最小。
2. 位姿图优化建图的研究意义(为什么需要PGO?)
在滤波方法来进行机器人的定位建图过程中,主要是来估算实时最新的位姿,而对于机器人的历史轨迹,并没有进行同时更新。这样导致在机器人在大范围的环绕运动又回到曾经到过地方的时候,所积累的误差难以消除。位姿图优化的方法来进行定位建图优势在于可以记录机器人运动过程中所积累的所有历史感知信息,并且可以从全局的角度,来综合使用历史感知数据进行全面优化机器人的轨迹。这样对于大范围中所积累的误差,就可以通过闭环优化来进行消除,可以实现全局的误差消减,从而提高定位建图的精度。
3. 位姿图优化建图的基本原理(PGO如何产生的?)
位姿图优化的方法来源于贝叶斯估计框架,通过数学手段的处理,将最大后验概率的计算,转化成为最小二乘问题。这里简述公式推导过程,熟悉或不感兴趣的读者可以直接跳过。
首先描述一下公式推导的基础:
- 贝叶斯公式 p ( x ∣ z ) = p ( z ∣ x ) ⋅ p ( x ) p ( z ) = η ⋅ p ( z ∣ x ) ⋅ p ( x ) p(x|z) = \dfrac{p(z|x) \cdot p(x)}{p(z)} = \eta\cdot p(z|x) \cdot p(x) p(x∣z)=p(z)p(z∣x)⋅p(x)=η⋅p(z∣x)⋅p(x)描述了后验概率(Posterior) p ( x ∣ z ) p(x|z) p(x∣z)与似然(Likelihood) p ( z ∣ x ) p(z|x) p(z∣x)和先验 p ( x ) p(x) p(x)之间的关系。
- 联合概率分布 p ( A , B ) p(A,B) p(A,B)可以写成条件概率分布 p ( B ∣ A ) p(B|A) p(B∣A)与全概率 p ( A ) p(A) p(A)的乘积: p ( A , B ) = p ( A ) ⋅ p ( B ∣ A ) p(A,B) = p(A)\cdot p(B|A) p(A,B)=p(A)⋅p(B∣A)
- 马尔科夫假设机器人的当前状态只与上个状态相关,与上个状态之前的不相关
对于后验概率$p(x_{0:t},m| u_{1:t}, z_{1:t}) $,可以按照贝叶斯公式进行展开,然后再应用联合概率分解与马尔科夫假设,可以计算如下:
p ( x 0 : t , m ∣ u 1 : t , z 1 : t ) = η ⋅ p ( z t ∣ x 0 : t , m , u 1 : t , z 1 : t − 1 ) ⋅ p ( x 0 : t , m ∣ u 1 : t , z 1 : t − 1 ) = η ′ ⋅ p ( z t ∣ x t , m ) ⋅ p ( x t ∣ x 0 : t − 1 , m , u 1 : t , z 1 : t − 1 ) ⋅ p ( x 0 : t − 1 , m ∣ u 1 : t , z 1 : t − 1 ) = η ′ ⋅ p ( z t ∣ x t , m ) ⋅ p ( x t ∣ x t − 1 , u t ) ⋅ p ( x 0 : t − 1 , m ∣ u 1 : t − 1 , z 1 : t − 1 ) p(x_{0:t},m| u_{1:t}, z_{1:t}) = \eta \cdot p(z_t |x_{0:t},m,u_{1:t}, z_{1:t-1})\cdot p(x_{0:t},m| u_{1:t}, z_{1:t-1})\\=\eta^{'}\cdot p(z_t|x_t,m)\cdot p(x_t|x_{0:t-1},m,u_{1:t},z_{1:t-1})\cdot p(x_{0:t-1},m|u_{1:t}, z_{1:t-1})\\=\eta^{'}\cdot p(z_t|x_t,m)\cdot p(x_t|x_{t-1},u_{t})\cdot p(x_{0:t-1},m|u_{1:t-1}, z_{1:t-1}) p(x0:t,m∣u1:t,z1:t)=η⋅p(zt∣x0:t,m,u1:t,z1:t−1)⋅p(x0:t,m∣u1:t,z1:t−1)=η′⋅p(zt∣xt,m)⋅p(xt∣x0:t−1,m,u1:t,z1:t−1)⋅p(x0:t−1,m∣u1:t,z1:t−1)=η′⋅p(zt∣xt,m)⋅p(xt∣xt−1,ut)⋅p(x0:t−1,m∣u1:t−1,z1:t−1)
对于上式,在等式两边分别取 log ( ⋅ ) \log(\cdot) log(⋅)操作,并假设概率是符合高斯分布,这样就可以得到最小二乘的目标函数,也就是位姿图优化所要优化的目标函数 ∑ ( i , j ) ∥ e i j − R i j T ⋅ ( p j − p i ) ∥ 2 \sum_{(i,j)}\|e_{ij} - \mathbf{R}_{ij}^T \cdot (\mathbf{p}_j - \mathbf{p}_i)\|^2 ∑(i,j)∥eij−RijT⋅(pj−pi)∥2。
4. 位姿图优化建图的算法流程(PGO 如何工作的?)
位姿图优化建图算法流程主要由构建位姿图,优化位姿图两大步骤所构成。
构建位姿图通常称为求解同时定位建图问题的前端,需要计算相邻节点之间的相对运动约束,以及非相邻节点之间的运动约束(包括临近节点之间的共视帧约束,以及闭环节点之间的闭环约束)。运动约束的构建,在激光定位建图中,主要通过扫描匹配来实现。激光扫描匹配是将两帧激光数据匹配到一起,使得其中一帧激光束的末端点,能够匹配到对应于空间同一个物体的另外一帧激光束的相应末端点上。
优化位姿图通常称为位姿图来求解同时定位建图问题的后端,主要求解图优化问题中所构建的非线性优化最小二乘问题,求解方法一般使用数学工具每次计算出来一个优化变量的增量,需要经过不断迭代,才能收敛到优化数值上。图【2】 描述了非线性优化最小二乘的迭代算法流程:迭代过程中会先构建出等效的线性求解方程,再计算出优化变量的增量;然后就可以将所计算出来的优化变量增量,叠加到当前的优化上面,以便触发下一个迭代的周期计算。在算法的迭代次数达到上限,或者所计算出来的优化变量对应的目标函数小于一定阈值的时候,就可以认为是达到优化收敛,此时的优化变量数值即为所求解的数值。

图【2】 非线性优化最小二乘的迭代算法流程
迭代优化求解方法中,比较常见的是高斯牛顿(Gauss-Newton)方法和莱文贝格-马夸特方法(Lenvenburg-Marqudart)方法。其中GN方法是使用一阶的雅克比(Jacobbian)矩阵的乘积来近似二阶的海森(Hessian)矩阵,LM方法是将GN方法的基础上来加上梯度下降(Gradient Descent)方法,通过系数来调节更侧重使用GN方法还是GD方法。图【3】 描述了使用LM方法来进行迭代的求解过程。
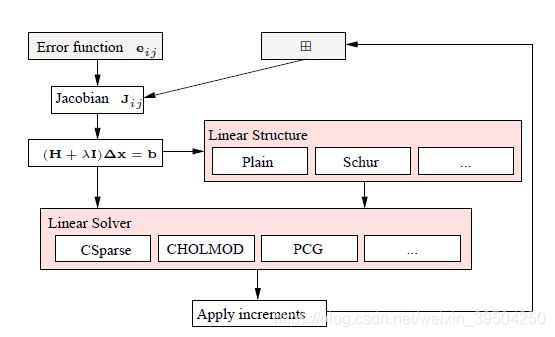
图【3】 使用LM方法迭代过程中的求解过程
对于非线性优化问题的求解,还有使用**随机梯度法(Stochastic Gradient Descend)**求解,SGD方法主要通过在梯度方向来进行选择合适的步长,实现优化的目的。由于上述方法的细节超出了本科普原理课程的范畴,这里不做展开详述。感兴趣的读者,可以参考文末所附参考文献。
5. 位姿图优化建图的性能改善(如何改善PGO?)
a). 构建充分有效的运动约束
由于该方法使用的是已知机器人一系列位姿下的建图方法,位姿图优化的机器人轨迹对于建图有着决定性的作用。要得到准确的优化结果,取决于位姿图的构建,也取决于位姿图的优化。优化过程是小节【b】即将展开描述的部分,本节主要讨论位姿图构建过程。只有确保及时构建出足够有效的运动约束,才能保证位姿图可以优化出有效的机器人轨迹。在帧间运动约束的基础上,需要及时构建出相临近帧之间的短距离共视帧约束,以及机器人回到曾经到过地方的闭环约束。于是,各种基于模板匹配的方法就很重要:比如基于激光模板GFLIP匹配的方法,基于视觉模板DBoW匹配的方法。具体细节感兴趣的读者可以参考相关文献,在附页中有写。
b). 目标函数中存在外点
位姿图优化中通过求解非线性最小二乘问题的最优解而得到所估算的机器人轨迹。如果目标函数存在外点(outlier),那么在优化的过程中就很可能会负面影响优化的结果。如果外点的占比较多,或者外点所对应的偏差较大,那么在优化的迭代过程中,就很难保证所计算的位姿更新增量是朝着使得目标函数变小的方向来进行。此时就很容易将迭代优化过程带偏,从而在迭代次数达到时优化变量难以及时收敛到正确的数值。
常用的应对外点的处理方法一般是使用带有抗干扰核函数的目标函数。目标函数通常意义上会被定义为偏差的平方二次型。抗干扰核函数主要针对偏差较大的情形,设置一个阈值来进行判断。如果偏差的绝对值大于阈值,那么相应目标函数的计算,就从原来的二次型偏差变换成为线性偏差。
还可以使用随机采样一致通过(Random Sample Consensus)的方法。该方法先在要优化的目标函数一系列子函数集合中,随机选取固定占比的子集来进行优化,从而得到相应的优化变量的解;然后使用该优化变量来计算目标函数,从而确定相应的内点百分比。如此方法,重复多次;每次都可以得到一组内点百分比。然后可以找到其中内点百分比最高的一组数据,使用这组数据来再次进行优化得到变量的数值。这样就可以得到与优化变量所保持一致的最大百分比数据所计算出来的数值,更加接近地面真值。
6. 参考文献
[1] Sebastian Thrun, Michael Montemerlo, The GraphSLAM Algorithm with Applications to Large-Scale Mapping of Urban Structures, The International Journal of Robotics Research, 2006
[2] Giorgio Grisetti, Rainer Kummerle, Cyrill Stachniss, Wolfram Burgard, A Tutorial on Graph-Based SLAM, IEEE Intelligent Transportation Systems Magazine, 2010
[3] Rainer Kummerle, Giorgio Grisetti, Hauke Strasdat, Kurt Konolige, Wolfram Burgard, g2o: A General Framework for Graph Optimization, 2011
[4] Gian Diego Tipaldi, Manuel Braun, and Kai O. Arras, FLIRT: Interest Regions for 2D Range Data with Applications to Robot Navigation, Int. Symposium on Experimental Robotics (ISER), 2010
[5] Bags of Binary Words for Fast Place Recognition in Image Sequences, IEEE TRANSACTIONS ON ROBOTICS, 2012
本讲总结
本讲描述了位姿图优化来进行建图的基本原理以及算法流程,并对其中可以改进提效的地方进行阐述:构建充分有效的运动约束,目标函数中存在外点相应处理。感兴趣的读者可以自行阅读参考文献中原文来探索更详细的全貌。