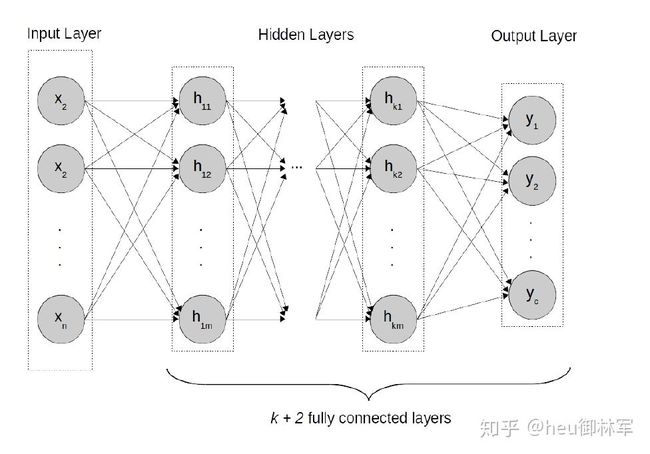
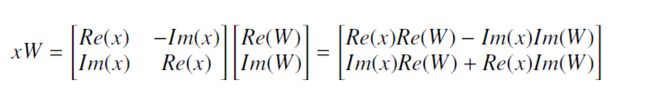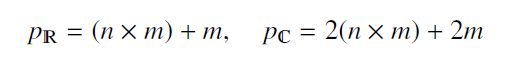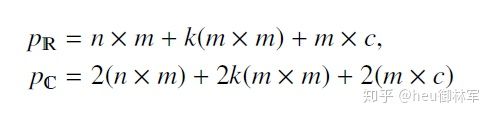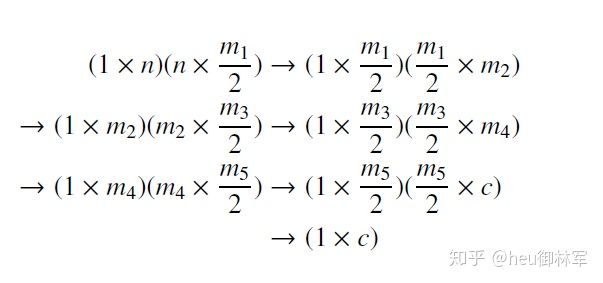深度学习论文分享:复值神经网络在实值分类任务中的应用
文章摘要
复值神经网络并不是一个新概念,然而,由于训练和性能方面的困难,使用实值模型往往比复值模型更受青睐。当比较实值与复值神经网络时,现有文献通常忽略参数的数量,从而导致神经网络与极大不同的比较。我们发现,当比较具有相似容量的真实和复杂神经网络时,复杂模型对于一系列实值分类任务执行等于或稍差于实值模型。复数的使用允许神经网络处理复杂平面上的噪声。当使用复值神经网络对实值数据进行分类时,权重的虚部遵循其实部。此行为对于不需要复值模型的任务具有指示性。我们在综合分类任务中进一步研究了这一点。我们可以使用不同的策略将许多激活函数从真实域转移到复杂域。然而,复杂神经网络的权重初始化仍然是一个重要问题。
文章引言
近年来,复值神经网络已成功应用于各种任务,特别是在信号处理,其中输入数据在复杂域中具有自然解释。复值神经网络通常与实值网络进行比较。我们需要确保这些架构在他们的模型大小和容量。比较的这一方面很少被研究或仅仅从表面上处理。一种其容量的度量标准是实值参数的数量。将复数引入模型会增加计算复杂度和实值参数的数量,但会假设权重和数据输入。本文探讨了具有可变深度和宽度的复值多层感知器(MLP)的性能。我们考虑实值的基准分类任务中的参数数量和激活函数的选择数据。我们提出了一个复杂值的多层感知器体系结构及其训练过程。我们认为各种激活函数以及复杂情况和实际情况下的实值参数数量。
我们建议构造可比网络的两种方法:
- 通过为每层设置固定数量的实值神经元
- 通过设置固定预算的实值参数。作为基准任务,我们选择MNIST数字分类[18], CIFAR-10图像分类[17],CIFAR-100图像分类[17]
相关工作
克拉克首先正式描述了复值神经网络[8]。此后有几位作者提出梯度下降的反向传播算法的复杂版本[6,10,19]。受多值工作启发1970年代的阈值逻辑[1],由Aizenberg等人定义了多值神经元和神经网络。[4,3]谁也将这个想法扩展到四元数。在2000年代,复杂的神经网络成功应用于各种任务[22、12、21、25]。这些任务主要涉及复杂值数据的处理和分析。或具有直观映射到复数的数据。特别是波形或傅立叶形式的图像和信号变换被用作复数值神经网络的输入数据[15]。复数的另一自然应用是在图像和信号处理中使用的卷积[7]。虽然真正的卷积在深度学习中广泛用于图像处理,但可以将其替换为复卷积[26、13、23、14]。复数和矩阵的属性可用于定义深度学习模型的约束。介绍了由Arjovsky等人撰写。 [5],并由Wisdom等人进一步开发。 [29]约束的复值递归网络它们的权重为单一矩阵,减少了消失或爆炸梯度的影响。最近,复值神经网络已被用来学习作为图像和音频嵌入的过滤器信号[27、24、9]。此外,张量分解已应用于复杂的嵌入以预测边缘知识库实体之间的关系[28]。尽管取得了成功,但复杂的神经网络没有其实际值对应部分流行。潜在地,因为培训过程和体系结构设计的直观性较差,这源于更严格的要求激活函数在复平面上的可分性[31,16,20]。在将复值神经网络与实值神经网络进行比较时,许多出版物都忽略了参数总数[3],仅比较整个模型的参数数目[26],否则不比较区分复数值或实数值参数和单位[30]。从本文的角度来看比较等效于比较不同大小的模型。我们系统地探讨了考虑激活函数,宽度和深度的简单分类任务中的多层感知器。
复值网络
我们定义一个类似于其实际值对应部分的复杂值神经元,并考虑其结构和训练上的差异。 复杂神经元可以定义为:
输入x∈ƒñ,W∈ƒn×m,b∈ƒ米上述定义中的激活函数φ可以是φ:ƒ→’或φ:ƒ→ƒ。 我们将考虑更详细地选择非线性激活函数。在这项工作中,我们选择一个简单的实值损失函数,但是复值损失函数可能会在将来工作。 上没有总订购复数的领域,因为i^2 = -1。 复值损失函数将要求定义一个偏序复数(类似于线性矩阵不等式)。
复数域中的训练过程有所不同,因为激活功能通常并非完全复杂。
复值网络中的参数交互
任何复数z = x + iy = r ∗ e我ϕ可以用两个实数表示:实部Re(z)= x和虚部Im(z)= y或等效于大小| z | =pX2 +年2 = r和相位(角度)ϕ = arctan(Xÿ)。因此,一个或多个复变量上的任何复值函数都可以表示为两个上的函数实变量f(z)= f(x,y)= f(r,ϕ)。尽管在神经网络中直接使用和表示,但复数定义了这两个部分。 考虑方程2概述的回归中必需的运算由实数和虚部(或等效地,幅值和相位)。 这种增强的表示形式有助于计算输入x与复数值权重的乘法矩阵W为:
网络的容量
(实值)参数的数量是一种度量网络的能力,可以量化网络在逼近结构复杂功能方面的能力。 参数过多时,模型倾向于填充数据,而参数过多时,则倾向于填充数据。 表示复数a +使用实数(a,b)的结果是,每一层的实数参数的数量加倍:pƒ= 2p'。 每层的实值参数的数量应在实值与其复杂值的体系结构之间相等(或至少尽可能接近)。 这样可以确保模型具有相同的容量。 性能差异是由引入复数作为参数而不是容量差异引起的。 在实际情况和复杂情况下,请考虑全连接层中的参数数量。 设n为输入维数,m为神经元数,则实值层p’和复数层pƒ的参数数由下式给出:
对于具有k个隐藏层且输出尺寸为c的多层感知器,无偏差的实数值参数的数量由下式给出:
乍一看,设计可比的多层神经网络架构是很简单的,即在每一层中具有相同数量的实值参数。 但是,将每层神经元的数量减半将无法实现参数可比性。 神经元的数量定义了一层的输出尺寸和下一层的输入尺寸。 我们通过选择具有偶数个隐藏层k和每个层之间的中子层数为m 2的MLP体系结构来解决此问题。我们在复杂值MLP的每个层中都将相同数量的实际参数与面积值网络相比较。 让我们考虑k = 4个隐藏层的输出和权重的维数。 对于实值情况:
其中mi是第i层的(复杂实数)神经元的数量。 复数神经元的等价使用为:
复值神经网络的激活函数
在任何神经网络中,一个重要的决定是非线性的选择。 在每一层中使用相同数量的参数,我们能够研究激活函数对整体性能的影响。 选择激活函数时要考虑的一个重要定理是Liouville定理。 定理指出,任何有界的全纯函数f:ƒ→ƒ(在整个复平面上都是可微的)必须是常数。 因此,我们需要选择无界和/或非全态激活函数。
为了研究假设函数在复杂参数中线性可分离的复杂模型的性能,我们选择了恒等函数。 这使我们能够识别在使用m个神经元时可能不是线性可分离的任务,而在使用mf个神经元时可能是线性可分离的任务。 一个例子是XOR函数[2]的近似值。 双曲正切是一个经过充分研究的函数,并且定义了复数和实数。 线性校正也很容易理解,并经常在实值设置中使用,但在复杂值设置中并未考虑。 它说明了在复数的两个部分上的单独应用。 选择幅度和平方函数可以将复数映射为实数。
复值网络用的激活函数有:
实验
为了比较实值和复值多层感知器(图1),我们在各种分类任务中对其进行了研究。 在下面的所有实验中,任务是使用复数值多层感知器为每个实数值数据点分配一个单一的类:
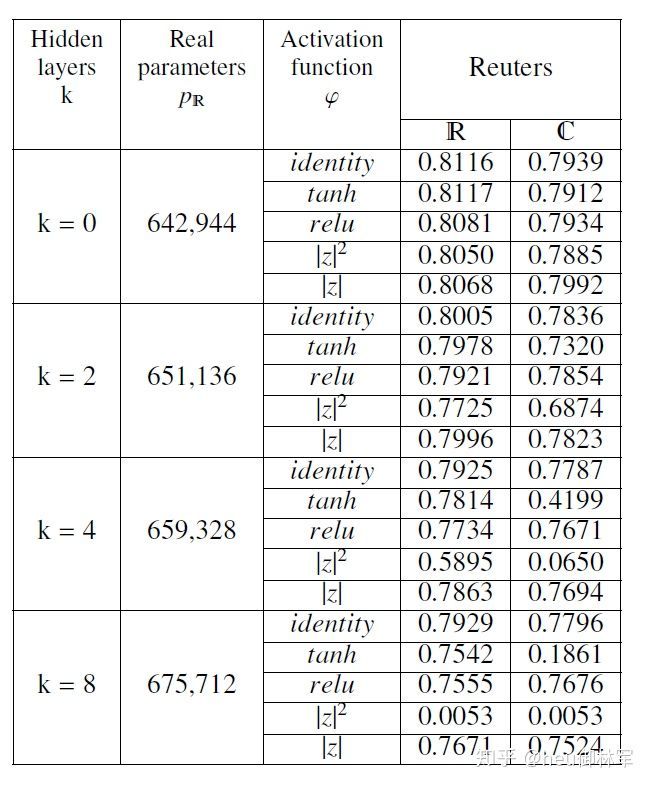
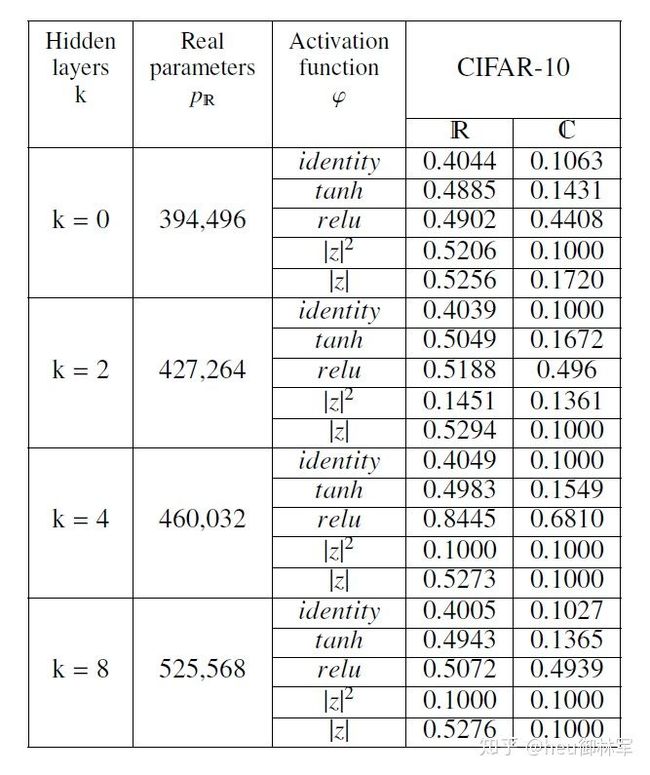
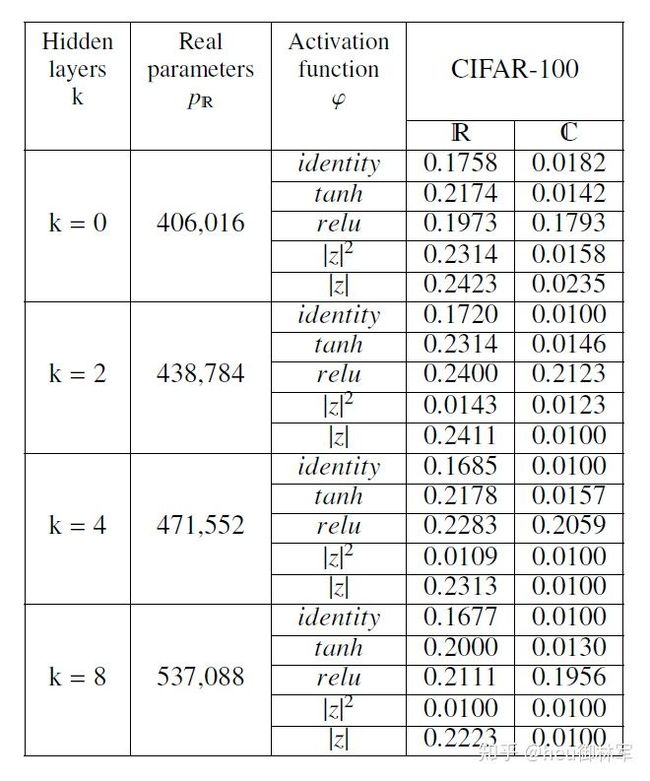
我们测试了具有k = 0、2、4、8个隐藏层的MLP,在实值架构中固定了每一层的单元宽度,在复数值架构中交替了64和32个单元(请参阅第5节)。 我们没有应用固定参数预算。 我们测试了MNIST数字分类,CIFAR-10图像分类,CIFAR-100图像分类和Reuters主题分类的模型。 路透社主题分类和MNIST数字分类每层使用64个单位,CIFAR-10和CIFAR-100每层使用128个单位。
得到以下的结果:
复数值MLP可用于将短依赖项(例如MNIST数字分类)或短文本分类为单词袋(例如路透社主题分类)。对于两个图像分类任务CIFAR-10和CIFAR-100,结果表明复合值MLP不会在数据中学习任何结构。这两个任务在第一层需要更大的权重矩阵,权重初始化仍然是一个重要的问题。复杂神经网络中最好的非线性是应用于虚部和实部的整流器线性单位relu,类似于实值模型。身份和双曲线正切值优于relu-特别是在实值情况下。但是,使用整流器线性单元relu的结果要稳定得多。尽管激活函数| z | 2和|| z |相似,但是它们在所有任务中的性能都显着不同。大小| z |始终胜过平方大小| z | 2。在这些分类基准中,激活函数是给定模型整体性能的决定因素。激活可以允许网络从错误的初始化中恢复并适当使用可用参数。
如预期的那样,我们观察到每层神经元的固定数量和深度的增加,复杂和实数值的准确性增加。随着参数总数的增加,模型的容量也会增加。这里是路透社主题分类的一个例外,即随着深度的增加,性能会下降。当根据给定的参数预算选择每层的神经元数量(使用公式17、18进行实验2)时,性能会随着模型深度的增加而显着降低。考虑到实验1的结果,每层的宽度比整个网络的总深度更重要。我们观察到10个初始化之间的性能差异非常大。我们假设,随着深度的增加,复杂MLP中的权重初始化变得困难得多。因此,它们的性能非常不稳定。我们通过对路透分类任务进行100次运行(而不是10次运行)训练一个复杂的MLP(k = 2,tanh)来确定这一点。结果显示出与其他结果相似的行为:性能差距减小
表1:在MNIST数字分类任务中,由k + 2层组成的多层感知器的测试准确性,每层具有64个神经元(在复杂的MLP中交替排列64和32个神经元),输出层具有c = 10个神经元(实验1) 。 十次最佳选择。 每次跑步训练100个回合。
表2:在路透社主题分类中,由k + 2层组成的多层感知器的测试准确性,每个层具有64个神经元(在复杂的MLP中交替排列64和32个神经元),输出层具有c = 46个神经元(实验1)。 十次最佳选择。 每次跑步训练100个回合。
表3:在CIFAR-10图像分类任务中,由k + 2层组成的多层感知器的测试精度,每层包含128个神经元(在复杂MLP中交替使用128和64个神经元),输出层具有c = 10个神经元(实验) 1)。 十次最佳选择。 每次跑步训练100个回合。
表4:由k + 2层组成的多层感知器的测试准确性,每层包含128个神经元(交替128个神经元)CIFAR-100图像分类中,复杂MLP中有64个神经元)和c = 100个神经元的输出层任务(实验1)。 十次最佳选择。 每次跑步训练100个回合。
对于涉及数据在复平面上有解释的许多应用(例如信号),复值神经网络已经显示出它们是优越的[15]。 我们工作中所有选定的任务都使用实值输入数据。 我们观察到,对于选定的任务,复值神经网络的性能不及预期,并且实值架构优于其复杂版本。 首先,这种发现似乎是违反直觉的,因为每个实数值只是虚数为零的复数的特例。 用复数值模型解决实数值问题可使模型有更大的自由度来近似函数。 为什么对复杂值模型进行分类时,为什么复杂值模型不如真实模型。 在进一步检查训练过程中,我们发现复数权重的虚部始终遵循权重的实部。
在达到分类的输入上,平面上虚部和实部作用相同。因此,分类是两个相同分类的平均值。如果在训练阶段,重量的虚部的平均绝对值遵循实部的绝对值,则输入的虚部与实部的分配方式完全相同,或者所考虑的任务根本不会受益于使用复杂的-有价值的假设。此外,我们观察到,与真实值神经网络相比,复杂值神经网络对其初始化更为敏感。灵敏度随着网络的大小而增加。权重初始化由Trabelsietal建议。[26]可以减少此问题,但不能解决。 Glorot等人的方差规模化初始化的这种初始化方法复杂。等[11]。其他可能的初始化方法包括使用随机搜索算法(RSA)[31]。这需要大量的计算。我们最终尝试通过不同的最小化来多次缓解每次实验的问题。但是,复数权重的初始化仍然是一个重要且尚未解决的问题,需要进一步研究。激活函数的无穷大会导致学习过程的数值不稳定。这可能会导致学习过程失败(例如,梯度实际上是无限的)。如果学习过程在功能上达到这一点(例如奇异性),则难以恢复训练。通过约束功能,标准化权重或渐变不可避免。随着深度和结构复杂性的增加,这些选择由于其计算成本而可能不切实际。或者,也可以在设计阶段通过选择有界且完全复杂的微分激活函数来避免这种情况。找到这样的功能是困难的。另一种可能性是通过应用单独的有界激活函数(相同或不同的实函数)来帮助解决该问题,从而在实践中避免该问题。整流器线性单元是这些功能之一。虽然不是完全可以区分的,但我们发现培训过程更加稳定并且性能得到了改善。尽管由于数学上的困难而存在差异,但实际上我们可以将许多见解从真实域转移到复杂域。总之,与具有相似能力的复值模型相比,实值模型对实值任务构成了较高的性能极限,因为实部和虚部对输入的作用相同。对信息和梯度流的研究可以帮助识别从复杂值神经网络中受益的任务。考虑到现有文献和我们的发现,我们建议,如果数据在复杂域中自然存在,或者可以有意义地移到复杂平面上,则应使用复杂的神经网络进行分类任务。网络应反映权重的实部和虚部与输入数据的相互作用。如果忽略该结构,则该模型可能无法利用更大的自由度。由于更复杂的训练过程,很可能还需要更多的初始化和计算时间。
结论
这项工作考虑了基准分类任务中复杂值和实值多层感知器之间的比较。我们发现,即使复杂值模型允许更大的自由度,复杂值MLP在对实际值数据进行分类时的表现也相似或更差。我们建议在神经网络中使用复数,如果a)输入数据具有自然映射到复数的功能,b)输入数据中的噪声分布在复平面上,或者c)可以从实值数据中学习复值嵌入。我们可以通过比较实际和虚构权重的训练行为(例如,通过平均绝对值)来确定从中受益的任务。如果假想部分在整个时期内都不遵循真实部分的一般行为,则该任务将从假设复杂的假设中受益。模型设计要考虑的其他方面是激活函数,权重初始化策略以及性能,模型大小和计算成本之间的折衷。在我们的工作中,性能最佳的激活功能是整流器线性单元在组件方面的应用。我们通过使用Wirtinger微积分或基于梯度的方法结合避免特定点的策略,将它们分别应用于两个真实部分,从而转移了许多真实和复杂的激活函数。 Trabelsi等人描述的初始化。 [26]可以帮助减少初始化问题,但是需要进一步的研究。与许多其他体系结构相似,引入复数作为参数也是决定在任务特定的性能,模型的大小(即实值参数的数量)和计算成本之间进行权衡的决定。