Unity脚本类 ---- Input类，虚拟轴与插值方法

 

 

1.注意第一个GetMouseButton（）方法只要检测到鼠标处于按下状态，那么该方法就会一直返回 true,鼠标没按下时调用该方法返回的是 false

2.而第二个方法 --- GetMouseButtonDown() 方法只会在你按下鼠标的第一帧返回一个 true，然后就一直返回false，GetMouseButtonUp()则是在你送开鼠标的那一帧返回 true，然后一直返回false

 

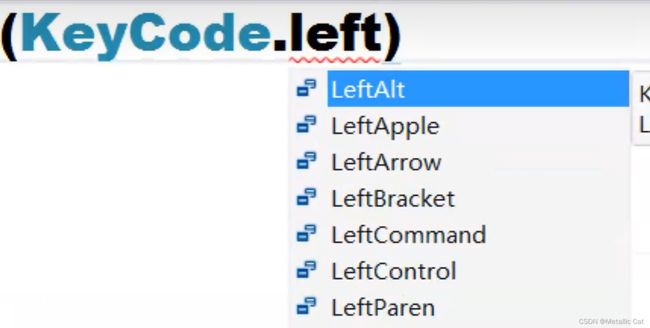
1.在KeyCode中ctrl这种左右堆成布局的按键对应的属性有两个，分别是 LeftCtrl 和 RightCtrl

2.有没有down / up ,取决于你想在按下对应按键后方法只执行一次还是执行多次。

（执行一次的话就有down/up，反之则没有）

 

1. 按照操作点开虚拟按钮面板之后，就能够看到18个Unity自带的虚拟按钮，如果我们将虚拟按钮个数（size）改为大于18的个数的话（如19个)，则Unity会自动创建新的虚拟按钮来补齐数目

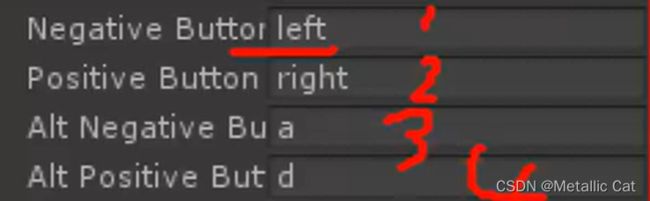
1.一个虚拟按钮分为正负两极，且一个虚拟按钮能够绑定四个真实按键，其中四个真实按键分为了两类：正向（positive）按钮和负向（negative）按钮

按了正向按钮绑定的真实按键后就会返回一个正值，负向按钮则是返回一个负值

 1.这两个输入框是用来描述正向按钮和负向按钮的功能的 --- 没有negative的是用来描述正向按钮的，有nagetive就是描述负向按钮

1.Gravity --- 复位速度

2.Sensitivity --- 灵敏度 

虚拟按钮有三个值 --- 1  - 0  - -1 ，当我们没有按到虚拟按钮对应的任何真实按钮时，虚拟按钮对应的值是0，按了正向按钮就会变到1，按负向就是变到-1，松开按键则值都会回到0

要注意的是这个变化不是跳跃式变化的，而是逐渐由0变1或者是由0变负1，而这个由0变化到其它值的速度就是由Sensitivity(灵敏度)决定的

而从1/-1变回0的速度则是由Gravity（复位速度）决定的

虚拟按钮除了可以绑定传统的键盘和鼠标按键之外，还可以绑定Mouse Movement(鼠标移动)

绑定鼠标移动的时候具体设置如上图：

1.

比较关键的是决定鼠标移动所绑定的移动轴，在上面这个设置中为x轴

2.绑定X移动轴之后，鼠标向右移动则虚拟按键值偏向1，向左移动偏向-1，保持不动则为0 

（MouseY则是对应鼠标的Y轴运动 --- 上为正，下为负）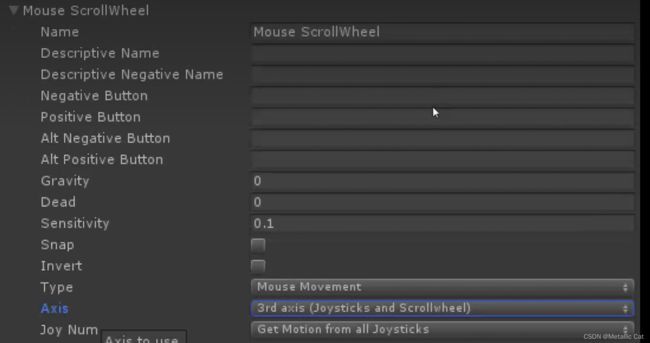

这一个虚拟轴对应的是鼠标滚轮 --- （Joysticks --- 操作杆，Scrollwheel --- 鼠标滚轮） 

1.虚拟轴在绑定像 ctrl , shift 这种具有左右对称排布特点的按键时，必须写明绑定的是 left 还是 right(绑定时不能用大写格式，只能用小写格式) 

2.绑定按键时，空格对应的是 space

前面三个方法能够起到的作用如下：

1.任何与给定虚拟轴绑定的真实按键处于按下状态的话，则该方法会一直返回 true

2.任何与给定虚拟轴绑定的真实按键被按下的那一帧，该方法会返回一次true

3.任何与给定虚拟轴绑定的真实按键被抬起的那一帧，该方法会返回一次true

后面两个方法则是

1.没按下与虚拟轴绑定的真实按键时调用该方法后会返回0，按下绑定的正向按键时会返回一个从0到1不断变化的单精度浮点数，按下绑定的负向按键则是从0到-1的一个单精度浮点数

2.没按下返回0，按了正向按键返回1，按了负向按键返回-1

3.有了虚拟轴之后，作为程序员的我们以后就不用再去找固定的按键了，只需要找到虚拟轴即可

4.对于绑定鼠标移动轴的虚拟轴 “Mouse X” 和 “Mouse Y”来说，由于我们在移动鼠标的时候并没有按下按钮，所有上面三个GetButton方法获得这两个虚拟轴的任何反馈的，只有两个GetAxis方法可以获得反馈（右下正，左上负）

1.有Raw，没Raw的区别就是是否应用平滑过渡

1.写摄像头沿着鼠标移动的脚本的时候要注意一个问题 --- 我们的鼠标左右移动时，摄像头是沿着世界坐标系的y轴旋转的，如果我们直接写下面这种类型的代码的话：

则都是沿自身坐标系旋转，因此如果想沿世界坐标系旋转的话，必须再给方法加一个参数：

指明沿哪一个坐标系旋转（摄像头上下摆动是沿着自身坐标系旋转的，而不是沿着世界坐标系，否则的话会导致上下摆动并不是我们想要的效果） 

---

 插值法

1.插值法是类 ---- Mathf 中的一个方法 --- Lerp方法

 

1.Lerp方法需要三个参数，分别是数据变化的起点，终点以及数据返回比例，该方法的工作逻辑如下：

一.确定当前数据起点和数据终点所在的数据段

二.按照第三个参数 --- 数据返回比例，从起点开始像终点前进对应比例（该比例的取值范围是0到1，如果取0.1的话则表示从起点开始，向终点前进整个段的0.1倍）

三.前进到指定位置后，将指定位置的数值返回

比如 --- Lerp（20，60，0.1）

1.数据段 = 60 - 20 = 40 ， 前进段 = 数据段 * 0.1 = 4

2.返回值 =  起点 +  前进段 = 20 + 4 = 24

知道了这个方法的执行逻辑后，我们就能够实现一个数值在一定数据段的由块到慢（或者反过来）的变化，具体的实现方式如下：

一.确定起点，终点，比例

二.令变化量等于起点，并调用Lerp方法，然后将调用后的返回值传给变化量，接着重复执行步骤2

按照上面这两步走，就能够得到一个以越来越慢的速度接近终点，且只能无限接近终点而到达不了终点的变化量

1.但是无限接近并不是我们希望出现的情况（不停的调用方法占用内存空间），因此我们可以对变化量进行一个判断 --- 即当变化量与终点的差值小于一定数的时候，直接令变化量等于终点值并结束调用方法，这样就能够使得无限接近结束掉。

2.使用上面这个方法还需要处理一个问题 --- 作差之后的值的正负问题 --- 可以通过调用 Mathf 中的 Abs方法来解决 --- Abs(参数) --- 调用后返回参数的绝对值

3.不要忘了浮点数在计算机中并不是精确存储的，而是采用近似存储的方式，因此对浮点数作判断的时候尽量不要使用 == 这种过于绝对的判断

---

1.在Unity脚本中创建一个具有 Public 权限的数组引用，并将脚本挂载到游戏物体上后，该游戏物体的Inspector界面处会出现如下参数输入窗口

这个Size指的是数组元素个数，填入后脚本会自动创建一个数组实例（该数组的元素个数与Size相同），并将具有Public 权限的数组引用指向该数组，同时Inspecor界面会出现如下变化：

即填入元素个数后，又会出现对应的元素赋值窗口，我们可以直接在窗口处对元素进行赋值。 这行代码能够实现当index从0开始不停的+1，加到等于zoomLevel.Length时又变回0的功能

（其原理就是取余的特性 ---- a%b , a < b 时 a%b = a ; a = b 时 a%b =0）