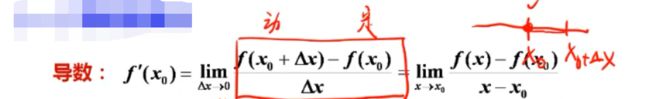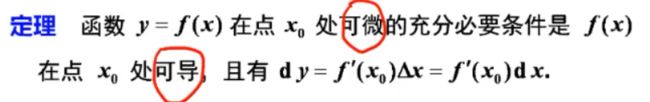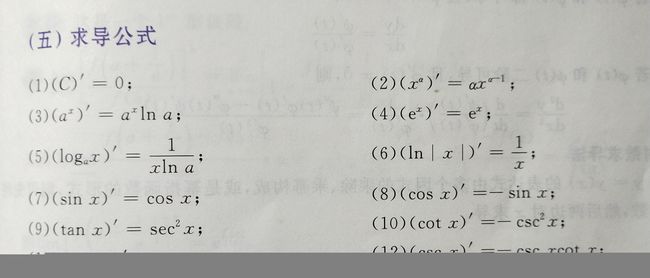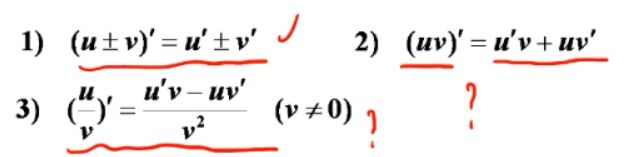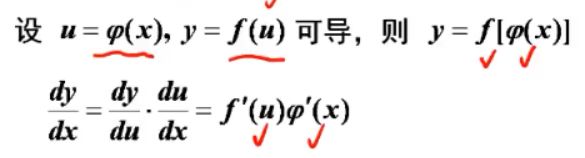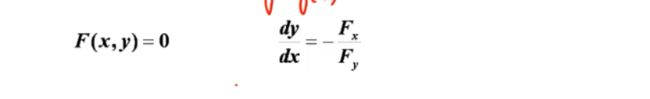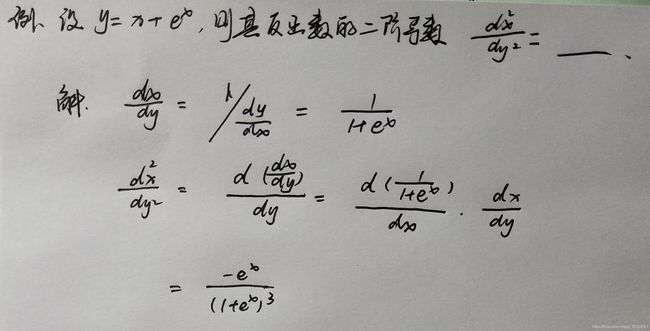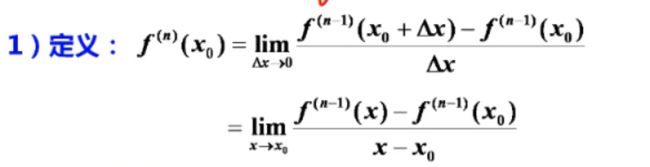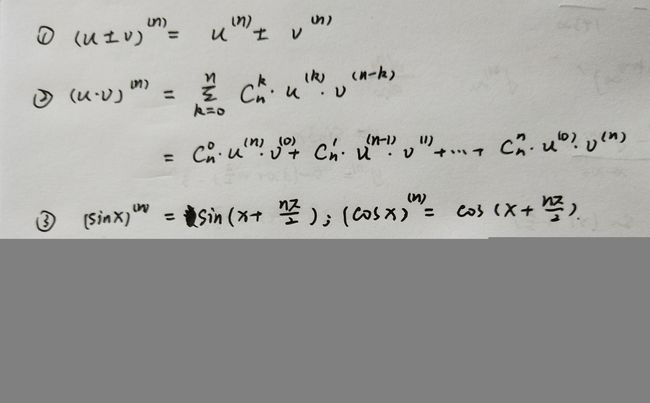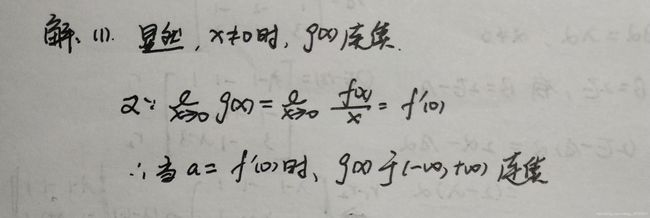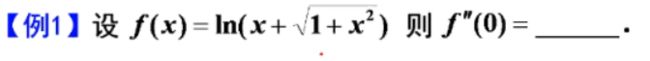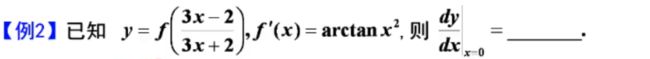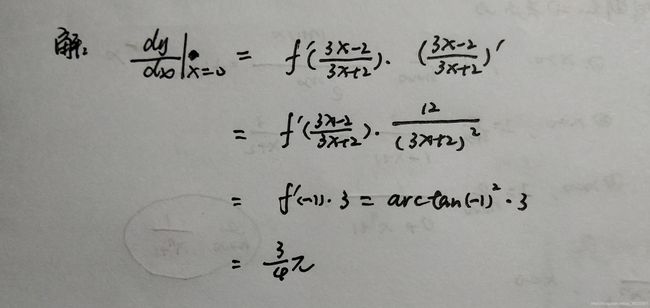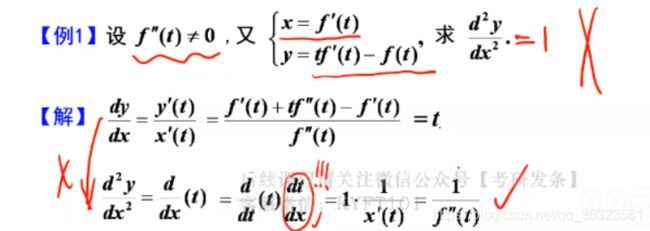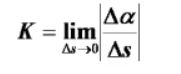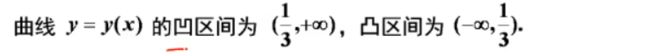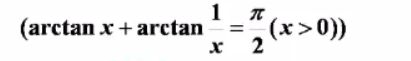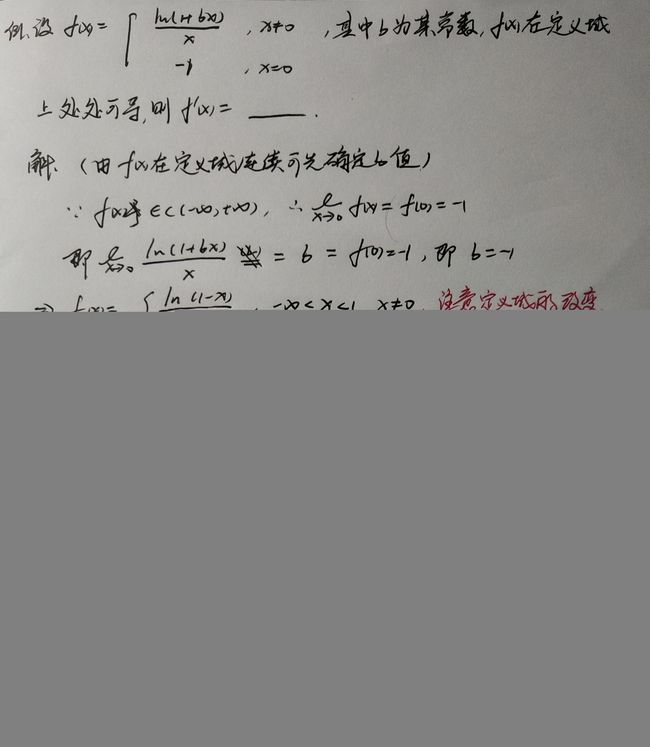第二章____一元函数微分学
大纲中包含两章:
① 导数与微分
② 一元函数微分学的应用
第一节 导数与微分
️ 2.1.1 概念理论
导数与微分的概念和理论
(一)导数的概念
导数的概念是难点
【定理】
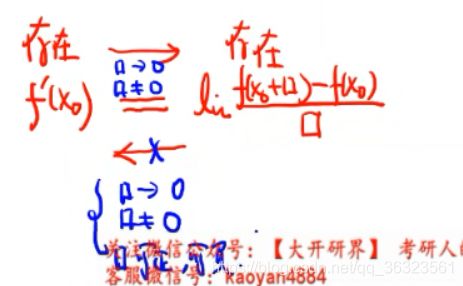
函数 f ( x ) f(x) f(x) 在点 x 0 x_0 x0 处可导的充分必要条件是它在该点处左导数与右导数都存在且相等。
》导数实质上是一个极限,函数量改变量与自变量改变量之比的极限;
这个极限反映了在这一点函数值相对于自变量的变化率;
》极限存在则称可导,极限不存在则称不可导
动点减定点才是变化率;
若均为动(定)点,则不是变化率
【*补】
设函数可导,
① 若函数为奇函数,则导函数为偶函数;
② 若函数为偶函数,则导函数为奇函数;
③ 若函数为周期函数,则导函数为周期函数,且周期相同。
(二)微分的概念
》上面说到,
导数是函数改变量的变化率
微分是函数改变量的变化率的近似值
函数在一点的改变量是随自变量改变量变化的,即 f ( x 0 + △ x ) − f ( x 0 ) f(x_0+\triangle x)-f(x_0) f(x0+△x)−f(x0) 为自变量改变量的一个函数;
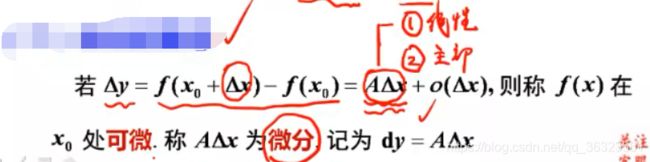
若函数的改变量可写成 A △ x + 0 ( △ x ) A\triangle x+0(\triangle x) A△x+0(△x) ,此时称函数在该点处可微
其中,称 A △ x A\triangle x A△x 定义为函数在这一点处的微分;
》之所以这样定义,是因为 A △ x A\triangle x A△x 有两大特征:
① A △ x A\triangle x A△x 是 △ x \triangle x △x 的线性函数
② A △ x A\triangle x A△x 是 △ y \triangle y △y 的主要部分
》所以说微分是函数改变量的近似值
微分是函数改变量的线性主部
》用微分近似地表示函数的改变量;就是用线性函数来近似这样的一般函数
》线性函数代表均匀变化,所以用微分代替函数改变量,实际上就是用均匀变化代替非均匀变化
这是处理非均匀变化的一个核心思想
在一个微小的局部,把一个非均匀变化的量,用一个均匀变化的量来代替,而均匀变化的量可以用线性的方法解决
考卷中经常考导数的概念以及可导性的判定,而很少考可微性的判定;
因为一元函数中,可导与可微是等价的;
用导数定义判定可导性,比用可微定义判定可微性方便很多;
{该定理的意义}
① 解决了可微的判定问题;
② 解决了可微的计算问题
微分等于导数乘自变量的改变量
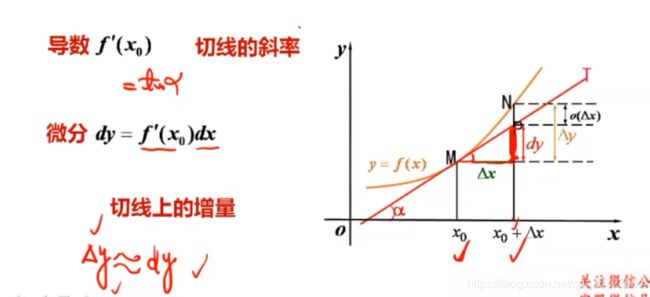
(三)导数与微分的几何意义
导数的几何意义:函数所对应的曲线在一点处切线的斜率
用微分来代替函数的改变量,
几何上就是用切线的改变量(均匀变化)来代替曲线的改变量(非均匀变化)
???
对于根号x在0处的切线的斜率怎么看?
是存在还是不存在?
导数肯定是不存在,但斜率存在不?
???
(四)连续、可导、可微之间的关系
不可将导数与微分混为一谈,只能说存在性相同
【例】
(五)补充
函数的左右导数,与导函数的左右极限无关,两者互相不可推之。
️ 2.1.2 基本运算
导数公式及求导法则
(一)求导公式
(二)求导法则
求导法有以下几种,
最核心的是前两种,解决了初等函数的求导问题
| 1 | 有理运算求导法则 ⭐️ | |
| 2 | 复合函数求导法则 ⭐️ | |
| 3 | 隐函数求导法则 | |
| 4 | 反函数的求导 | |
| 5 | 参数方程求导法 | |
| 6 | 对数求导法 |
① 有理运算法则
② 复合函数求导法则
【例】
③ 隐函数求导法则
④ 反函数的求导
若 y = f ( x ) y=f(x) y=f(x) 在某区间内可导,且 f ′ ( x ) ≠ 0 f'(x)\neq 0 f′(x)=0 ,则其反函数 x = ϕ ( y ) x=\phi(y) x=ϕ(y) 在对应区间内也可导,且
ϕ ( y ) = 1 f ′ ( x ) ; 即 d x d y = 1 d y d x \phi(y)=\frac{1}{f'(x)};即\;\; \frac{dx}{dy}=\frac{1}{\frac{dy}{dx}} ϕ(y)=f′(x)1;即dydx=dxdy1
【例】
⑤ 参数方程求导法
⑥ 对数求导法
一般遇到连乘或连除,可选择对数求导法
️ 2.1.3 高阶导数
(一)高阶导数的概念
(二)常用的高阶导数公式
️ 【补充】
【f(x) 与 |f(x)| 可导性的关系】
️ 2.1.4 常考题型与典型例题
强化班题型归类
题型一 导数与微分的概念
(一)利用导数定义求极限
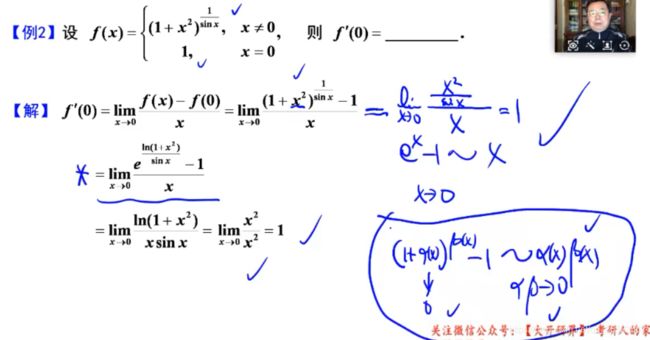
【例】
【例】
【例】
【例】
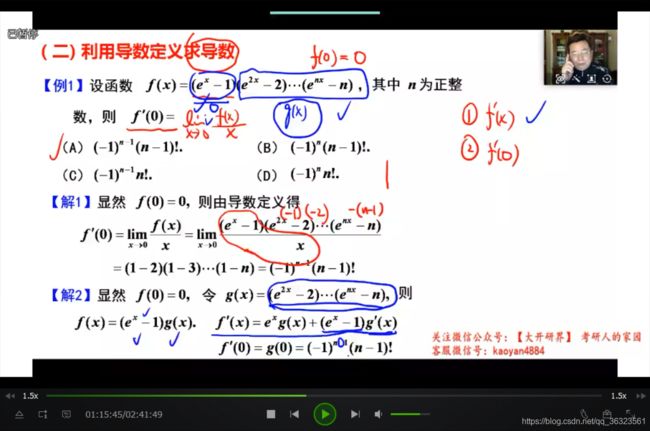
(二) 利用导数定义求导数
分段函数在分界点处求导一般都用导数定义
【例】(技巧题)
【例】(常规题)
【例】(常规题)
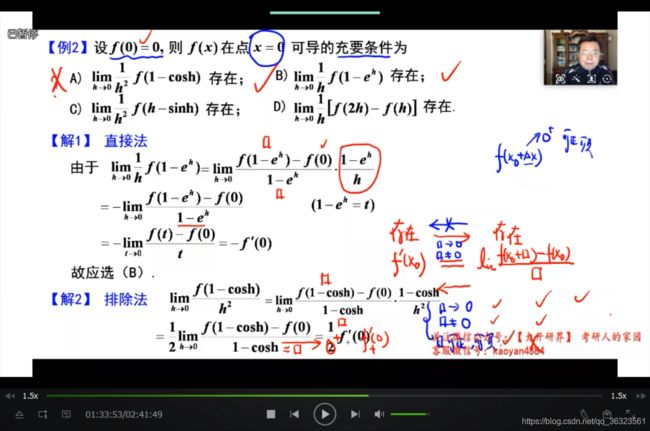
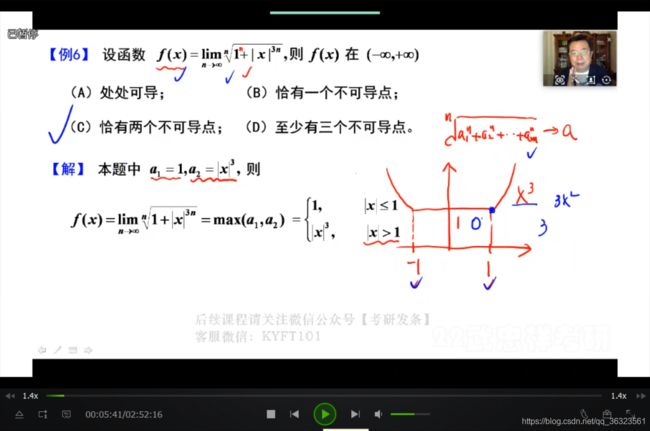
(三)利用导数定义判断函数可导性⭐️
既是重点也是难点
此处归纳该种题型有哪些出题方式,解题的一般方法是什么
【例】
【例】
【例】注意结论
【例】【真】
结合上一题的结论
【真】
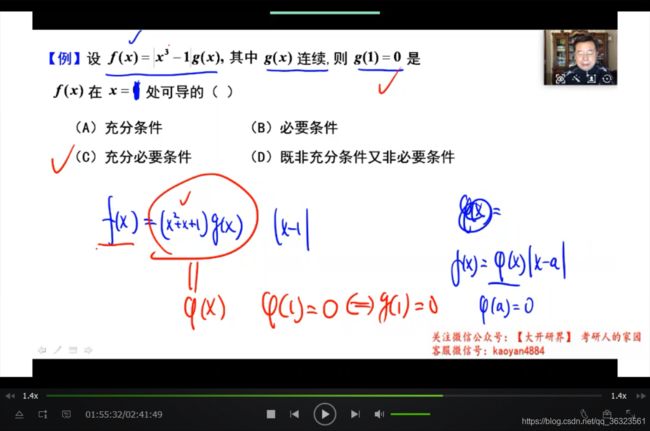
【例】函数可导性与绝对值可导性之间的关系
【例】
【例】
证明连续一阶导数,需要证两点
1、一阶导数存在
2、一阶导函数连续
》二阶可导不能保证二阶导函数连续,甚至不能保证二阶导数有极限
》在洛必达不能继续进行时,往往可采用导数定义
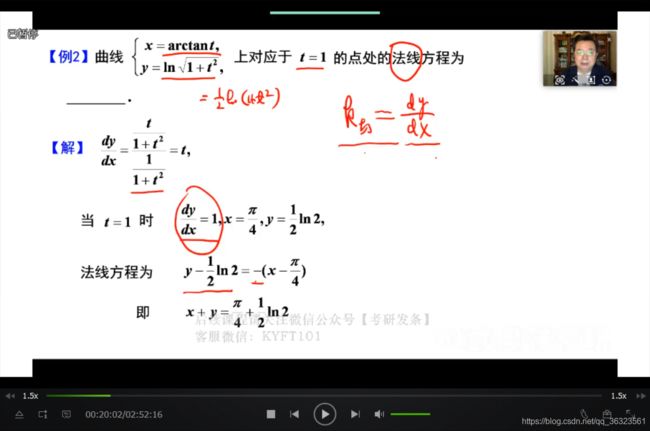
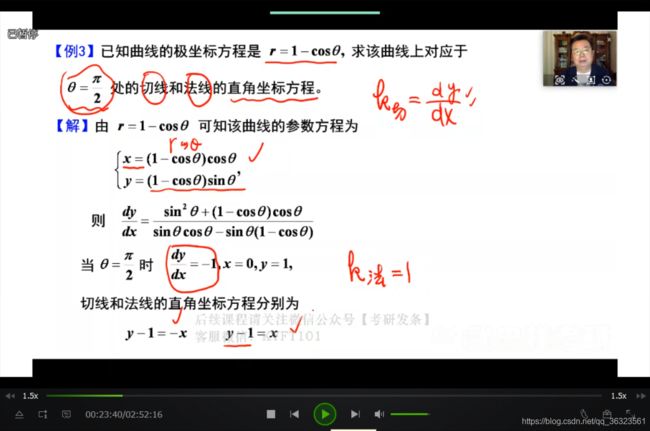
题型二 导数的几何意义
常考平面曲线方程,常有三种
直角坐标系下、参数方程形式、极坐标下
曲线的切线、法线等
【例】
【例】
【例】
【例】
题型三 导数与微分的计算
一、复合函数求导
【例】(常规题)
》描述:常规的复合函数求导
》补充:结合了
- 常见的奇偶函数
- 奇(偶)函数的n阶导的奇偶性
【例】
【例】
【例】
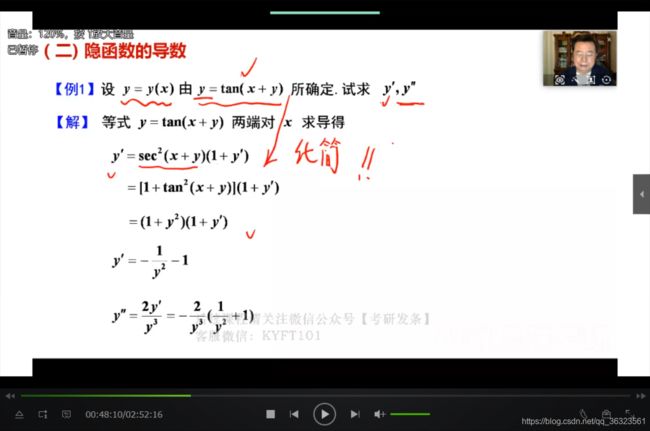
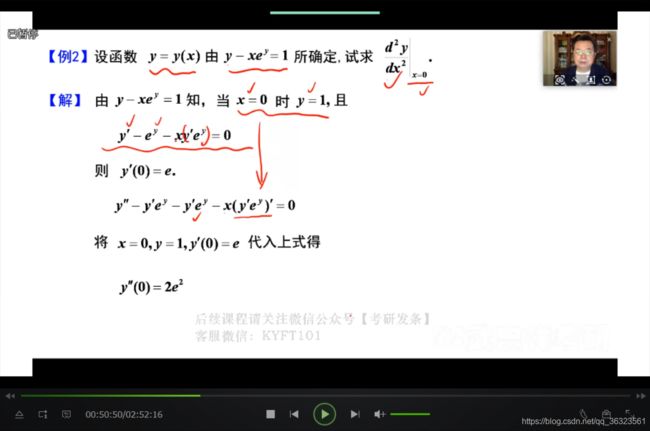
二、隐函数求导
【例】
【例】
【例】
三、参数方程求导
【例】
【例】
四、反函数求导
考频不高,但不可忽视
【例】
五、对数函数求导法
【例】
遇到连乘连除,求导不方便,可采用对数求导法
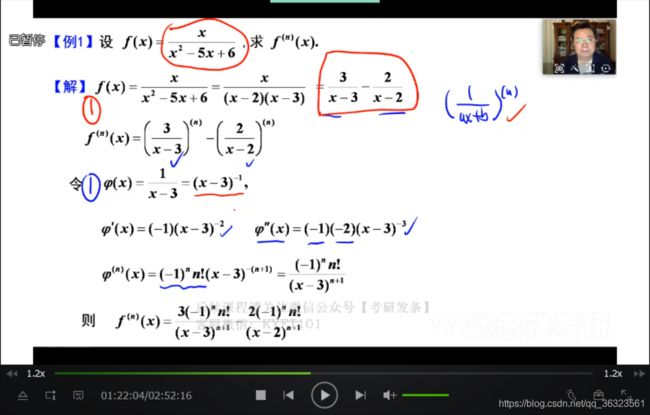
六、高阶导数
常用方法:(三种方法)
1、用已知公式
2、通过求前几阶的导数,归纳n阶导数
3、利用泰勒级数(公式)
其中,
方法一、二用作求n阶导函数
方法三,适用于具体点
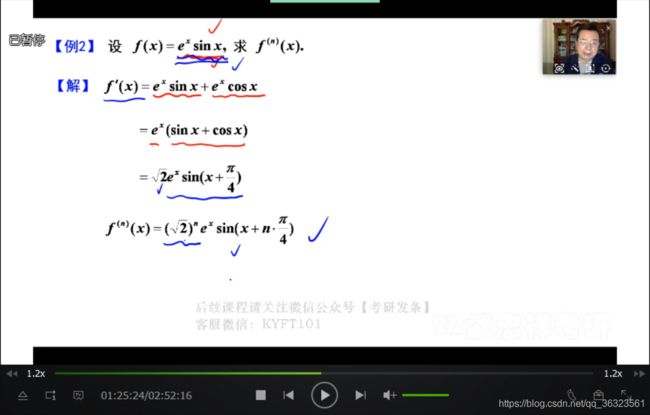
【例】
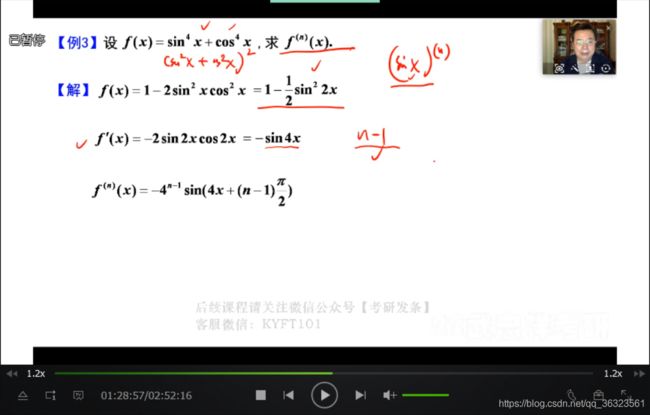
【例】
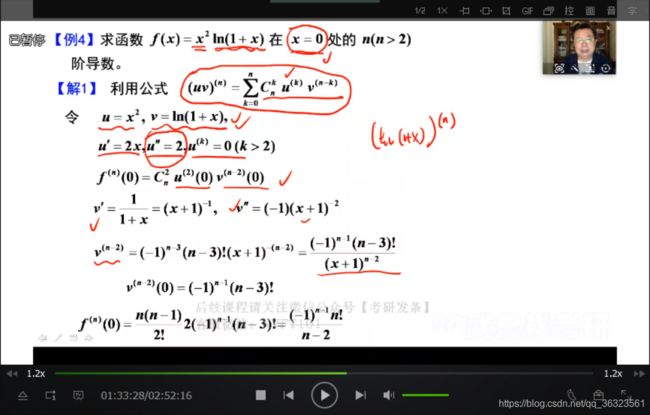
【例】
【例】
第二节 导数应用
️ 2.2.1 微分中值定理
微分中值定理是基础;
是建立导数与函数的桥梁
此处共四个微分中值定理
(未包含积分中值定理)
前三个微分中值定理建立了一阶导数与函数之间的关系
而高阶导数与函数之间的关系由泰勒中值定理(带有拉格朗日余项的泰勒公式)来建立
泰勒有两个,
一个叫皮亚诺余项的泰勒公式,研究局部性态,又称局部泰勒公式 (极限部分已讲解);
一个叫拉格朗日余项的泰勒公式,研究整体性态,又称整体泰勒公式
通常将带有拉格朗日余项的泰勒公式也叫做泰勒中值定理
》理论上,罗尔定理是拉格朗日中值定理的特例,即罗尔可证明的题,拉格朗日一定可证明(证明难度有区别)
同样,拉格朗日与柯西也是同样的关系
》罗尔定理虽然是拉格朗日以及柯西的特例,
但拉格朗日以及柯西都是构造辅助函数后,用罗尔定理证明所得,
注意体会罗尔定理的重要性
》中值定理中有一大堆题,都是构造辅助函数用罗尔定理证明(关键在于辅助函数的构造)
》四大中值定理之间的关系
泰勒中值定理中,取n为零,则成拉格朗日中值定理(拉是泰勒的特例)
【有关局部与整体】
【局部泰勒公式与整体泰勒公式】
首先要区分局部泰勒公式与整体泰勒公式
带有佩亚诺余项的为局部泰勒公式;
带有拉格朗日余项的为整体泰勒公式
【局部性态与整体性态】
局部性态: 只和一点的临近有关,叫做局部性态,如:极限、极值
整体性态:和极值对应的最值,因为最值是在一个区间上,强调的是整个区间的性态,而非一点临近的性态;
以及不等式,不等式强调的也是区间,既然是区间,则一定是整体性态,用整体泰勒公式
️ 2.2.2 极值与最值
关于极值这里,注意一个必要条件和三个充分条件
1、极值的概念
2、极值的必要条件
一阶导为零
当无可导的条件时,极值点与驻点无关
在可导的条件下,
极值点可推驻点,
驻点不可推极值点
言外之意:一个函数可导,则极值点只有可能在驻点上取
在不可导的地方,极值点只可能在导数不存在的点取到
3、极值的充分条件
极值共有三条充分条件
| 1 | 第一充分条件 | |
| 2 | 第二充分条件 | |
| 3 | 第三充分条件 |
(1)第一充分条件
第一充分条件:看驻点两侧一阶导数是否变号
变号,是极值;不变号,不是极值
当然,极值也可能存在于导数不存在的点,所以,若一点的一阶导数不存在,此时是否可用第一充分条件判定?
所以在第一充分条件里,附加了一个条件(函数在一点连续)
故此时,若一点处无导数,但在这一点处连续,仍然可以用第一充分条件判定
所以第一充分条件可以判定两种点:
1、驻点
2、导数不存在的点
(2)第二充分条件
在函数的条件比较好,在有二阶导数且不为零的情况下,第二充分条件比较适用
局限性在于只能判定二阶可导的函数
(3)第三充分条件
注意:第三充分条件完全有可能作为证明题考查
利用泰勒联系高阶导数与函数解答(这里研究极值,属于局部形态,故用局部泰勒公式,即皮亚诺余项的泰勒公式)
s1、先找所有可能取得的极值点(即驻点,和导数不存在的点这两种)
s2、用充分条件做判定
对于导数不存在的点,只可用第一充分条件,通过两侧是否异号判定;
对于二阶导、n阶导都有的点,则可以考虑第二、三充分条件
4、函数的最值
(1)最值的理论问题
在证明唯一极值点就是最值点时,采用反证法:
若对于唯一极值点,若x0不是最值点,则说明存在极值x1,又因为函数连续,故会导致x0与x1之间至少又存在一个极值点,与唯一极值点矛盾。
(2)最值的应用问题
️ 2.2.3 曲线的凹向与拐点
1、曲线的凹凸性
一阶导数的正负反映函数的增减性
二阶导数的正负反映函数的凹凸性
2、曲线的拐点
| 极值 | 拐点 | |
|---|---|---|
| 必要条件 | 一阶导为零 | 二阶导为零 |
| 第一充分 | 一阶为零,两侧一阶变号 | 二阶为零,两侧二阶变号 |
| 第二充分 | 一阶为零,二阶不为零 | 二阶为零,三阶不为零 |
| 第三充分 | 1~(n-1)阶均为零,n阶不为零 此时 不为零的n阶导数阶数为偶数,则是极值;否则非极值 |
2~(n-1)阶均为零,n阶不为零 此时 不为零的n阶导数阶数为奇数,则是拐点;否则非拐点 |
️ 2.2.4 曲线的渐近线
1、渐近线
共有三种渐近线
| 1 | 水平渐近线 | |
| 2 | 垂直渐近线 | |
| 3 | 斜渐近线 |
(1)水平渐近线
一条曲线的水平渐近线最多有两条
(2)垂直渐近线
(3)斜渐近线
一条曲线最多可由两条斜渐近线
注:
》在负无穷或正无穷的一侧,水平与斜最多只能存在一个
》三种渐近线,斜渐近线求解最复杂,但解法多样
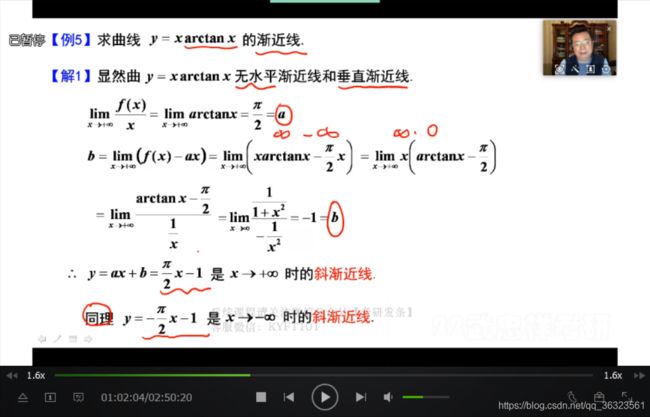
2、斜渐近线的求解
两种思路:
① 传统的求解a和b
②
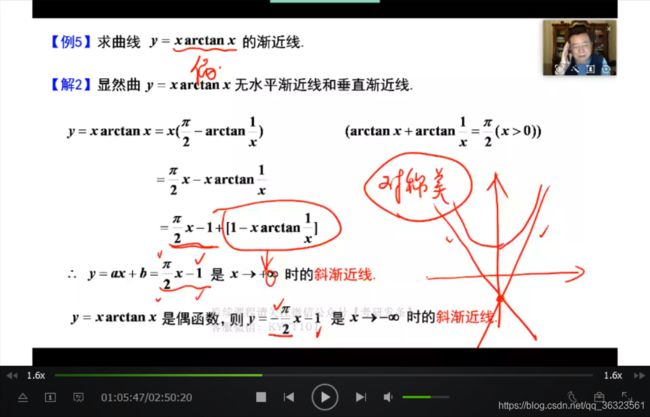
对于简单函数,即可写成线性函数,可通过线性函数加无穷小的方式解题;
对于复杂函数,即不可写成线性函数,一般方法是通过泰勒公式将函数写成多项式
即,一般用线性函数加无穷小的方式,不得已情况下再请泰勒出马。
️ 2.2.5 平面曲线的曲率
描述曲线在一点处的弯曲程度
1、曲率的定义
2、曲率的计算
3、曲率圆与曲率半径
曲率圆的几何意义需要掌握,属于可考内容
️ 2.2.6 常考题型与典型例题
题型一、二属于基础题,简单
题型三、四属于综合题,较难
题型五最难
(考研数学难题一般出在高数部分,高数部分的难题一般是中值定理相关的证明题)
题型一 函数的单调性及极值
基本题型,不可丢分
【例】求函数单调区间、极值
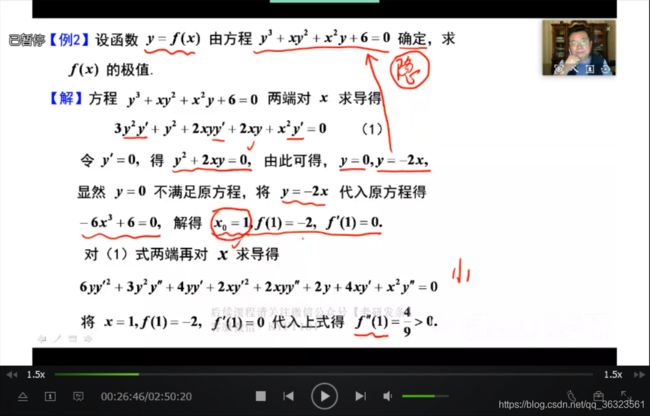
【例】隐函数求极值
【例】判极值
{描述}:常规题,利用第一充分条件判断
{补充}:保号性的条件是去心邻域,故不能得出0处的二阶导为正,实际上0处的二阶导为零
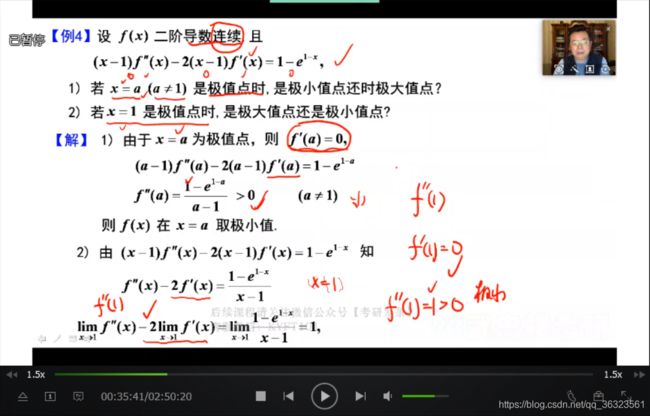
【例】
{描述}
{补充}:本题利用连续的条件
在(2)中,需要求解 f ′ ′ ( 1 ) f''(1) f′′(1) 但又不能代入 x = 1 x=1 x=1 ,故可以利用连续的条件,
将“0”因子除过去,此时不可直接代,可通过取极限,使计算得以进行
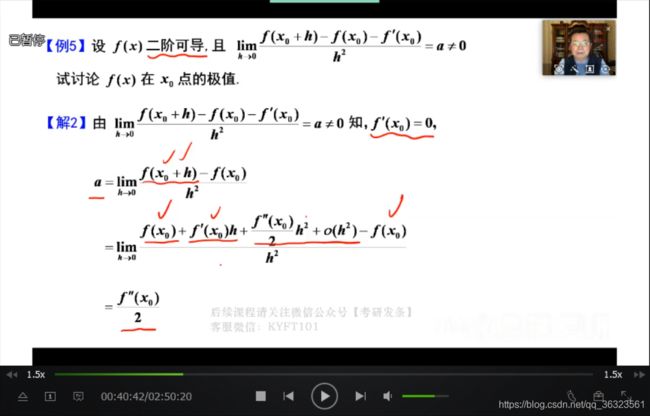
【例】
{补充}:函数二阶可导,在使用洛必达时,最多可出现一阶导
解法二:
因为极值是局部性态,可以用皮亚诺余项的泰勒公式
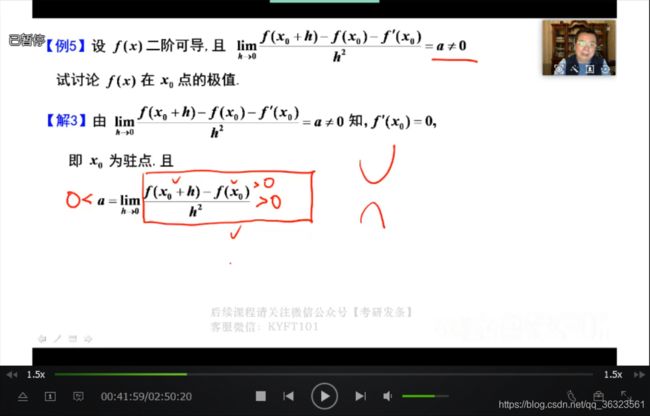
解法三:利用极限的保号性、极值的定义
题型二 曲线的凹向、拐点、渐近线及曲率
基本题型,不可丢分
//对于斜渐近线
【例】
【例】参数方程求极值
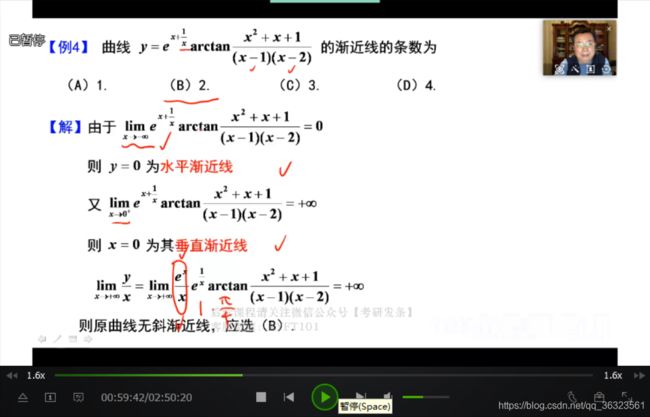
【例】求斜渐近线
【例】求渐近线
【例】
题型三 方程根的存在性及个数
方程根的问题其实是两类问题:
第一类 存在性问题 第二类 个数问题
1、存在性问题
两类方法
(1)连续函数的零点定理
(2)罗尔定理
若零点定理不方便,常指两端点异号这个条件不好实现,则采用罗尔定理
2、个数问题
两类方法
(1)单调性
说明个数问题常用单调性
(2)罗尔定理的推论
如果单调性不好用,则用罗尔定理的推论
*3、两类问题的进阶常常含有参数
含有参数的方程根的问题,对于含有参数的方程根的问题在解答时常用一种特殊方法,就是将参数分离,常会使处理变得简单很多
综合题型
【罗尔定理推论的证明】
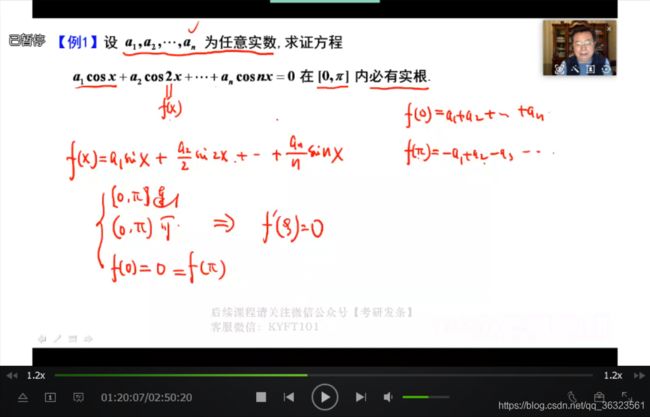
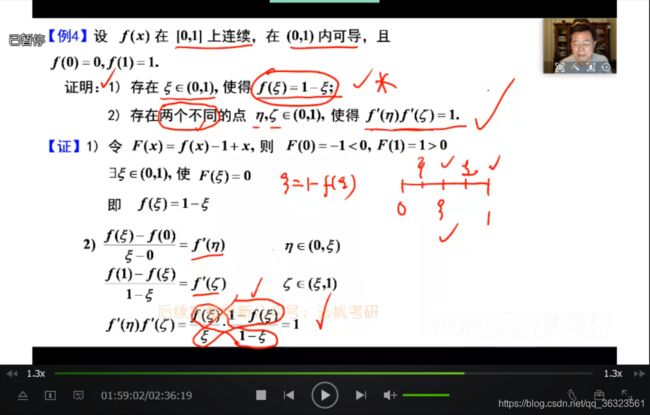
【例1】证明存在性
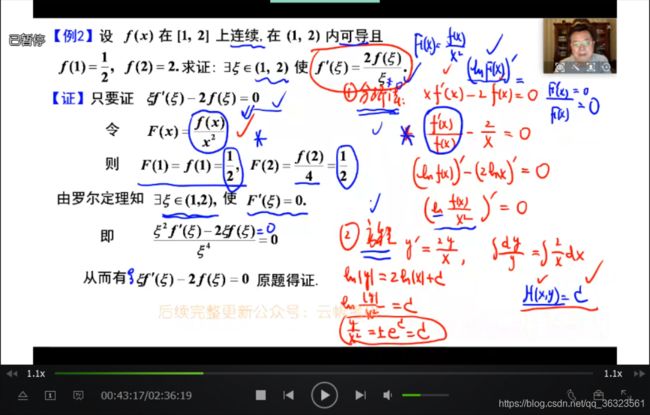
【例2】
【例3】
【例4】善用罗尔定理的推论
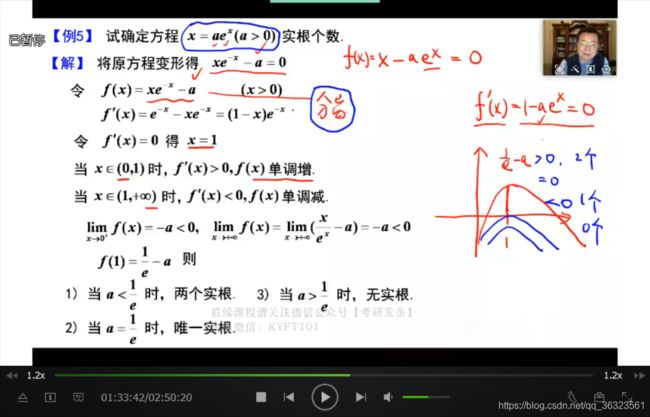
【例】由参数判根的个数
{补充}:注意题干的隐藏条件,x的定义域
最佳形式:导数为零的点与参数无关,即导数中无参数
故提取出参数再求导
》实际上更推荐令不含参数的部分为一个新的函数
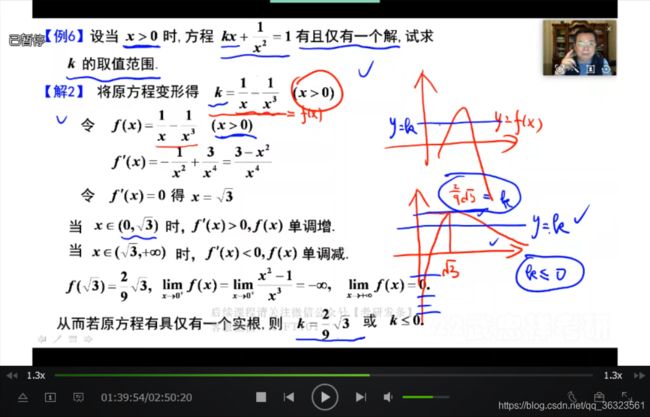
【例】由根的个数判参数
【例】
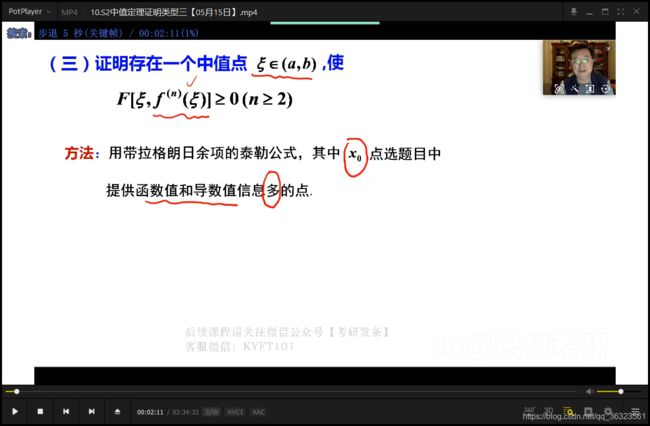
【例⭐️】
泰勒公式的系数,是由一点的各阶导数导数值表示,故对题干中信息最多的点使用
解法一的目标是证明存在一点小于0,那么不用泰勒是否也可?
题型四 证明函数不等式
综合题型
证明不等式常有五种方法:
| 1 | 单调性 | |
| 2 | 最大最小值 | |
| 3 | 拉格朗日中值定理 | |
| 4 | 泰勒公式 | |
| 5 | 凹凸性 |
1、单调性
最常用的方法,通常将不等式移到一边,构造函数,再用单调性解答。
4、泰勒公式
证明不等式用的是整体泰勒公式,即带有拉格朗日余项的泰勒公式
5、凹凸性
因为凹凸性就是由不等式定义的,所以不等式的证明可用凹凸性
注:五大方法中,前三种最常用;前三种中,最常用的是单调性
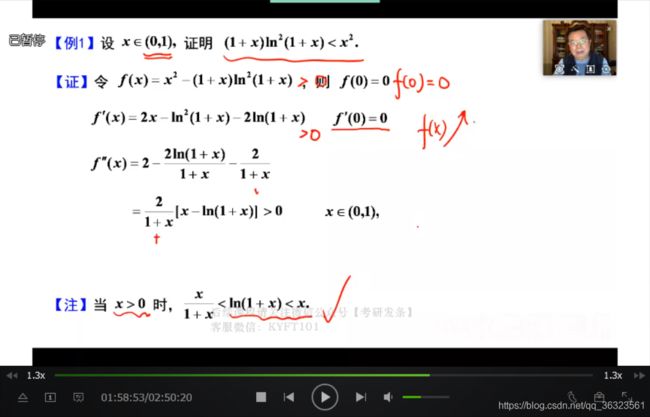
【例】
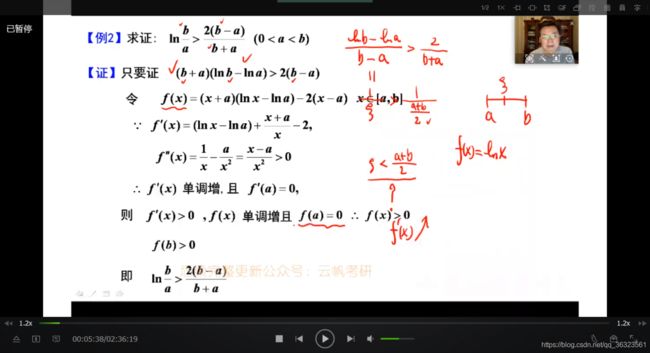
【例2】
{补充}:本题中值定理不适用,因为不能保证中值的存在范围;故利用单调性解题
//此外,需要记住,构造的函数是为了服务于解题。构造的函数在定义域内的任意取值都可认为是在重新构造函数
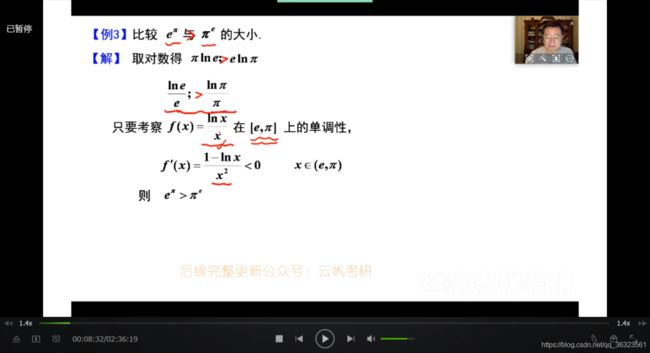
【例3】
{描述}:取对数,构造同一函数不同取值下的大小比较问题
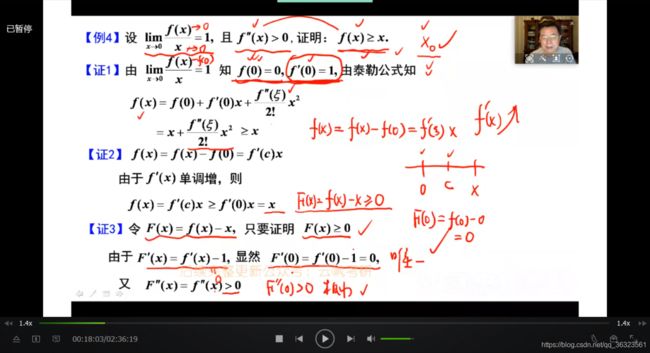
【例】
① 为什么想到用泰勒中值定理?
答:题干中,由二阶导数问题求证函数的大小比较问题,即高阶导数与函数之间的问题求解,首先想到的是泰勒中值定理;其次,研究区域为R,故用整体泰勒(拉格朗日余项)。
② 为什么想到在x=0处展开
答:展开的选择取决于哪一点函数导数值所知信息多。
【例】
在这里插入图片描述
题型五 微分中值定理有关的证明题
难题高频出题考点
总得来说,可以概括为三大问题
| 第一类 | 含有一阶导 | 构造辅助函数,利用罗尔定理 |
| 第二类 | 双中值类型 | 分离简单部分用拉格朗日 |
| 第三类 | 用带拉格朗日余项的泰勒公式 | |
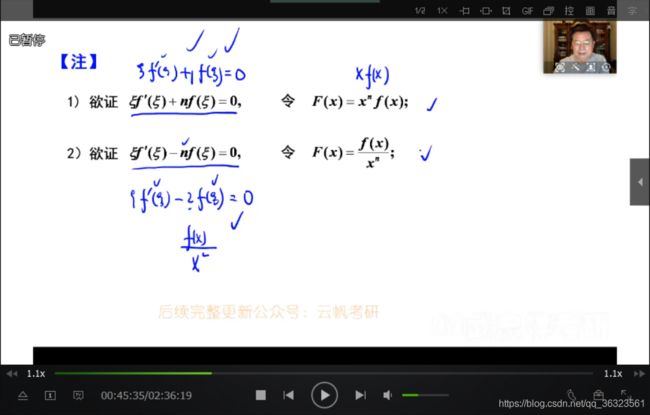
类型一、(变量、函数、一阶导)型
这里的一阶导不是指具体的一阶导函数,实际上是指为了找到其原函数而描述的一阶导,如例7
形式 其中,变量、函数存在与否不限定,但一阶导一定要存在 核心思想 构造辅助函数,用罗尔定理 其中,构造辅助函数有2+1种方法:
分析还原法 微分方程法 利用总结的规律(熟练可首选)
【例】
【例】
【例】
【例】
【例】
{}
{补充}:所构造的辅助函数不是唯一的,取决于选择辅助函数的方法
第(1)问 解法一:分析构造法找辅助函数 解法二:不借助辅助函数,利用拉格朗日中值定理求解 第(2)问 解法一:利用已知规律找辅助函数 解法二:微分方程法找辅助函数 解法三:不同的构造函数
【例6】
第(1)问 解法一:传统方式,反证法 解法二:利用罗尔定理的推论 第(2)问 分析还原法找辅助函数
【例7】
{描述}:
{补充}:变上限积分求中值点,看似无导函数存在,实际含有
该类题型主要利用规律找到辅助函数从而使用罗尔定理,仍是含有“导数”
【例】
{描述}:具有一定的综合性,将微分中值定理同积分中值定理综合
{补充}:罗尔定理条件不足,需要获取条件
// 显然,由规律得辅助函数。
// 本题在找出辅助函数后,需要使用罗尔定理证得结论,但需要找到两函数值想等的条件。
这里由题干看出,通过借助积分中值定理可以获取到这个条件。
【例9⭐️】
{补充}:注意这里辅助函数构造的手法
注意:
推导过程中的 F ( x ) F(x) F(x) 这个表达式在 x = 0 x=0 x=0 处是无定义的;
但可以人为构造出 x = 0 x=0 x=0 这一点有定义(此时实际上是更新了 F ( x ) F(x) F(x));
又因为构造出的 F ( x ) F(x) F(x) 需要满足罗尔定理闭区间连续的条件,所以需要用连续性求得 F ( 0 ) F(0) F(0)
类型二、双中值问题
这是一般形式,即表达式中两个一阶导必须出现,其余的可以不出现。
对于双中值定理的问题,需要使用两次中值定理,主要分两类问题
方法 case1 要求低 (双中值可以相同) 同区间两次中值定理(拉格朗日、柯西) case2 要求高 (双中值不同) 分区间两次中值定理(难点在于分点的选取)
case1、要求低(不要求两中值不同)
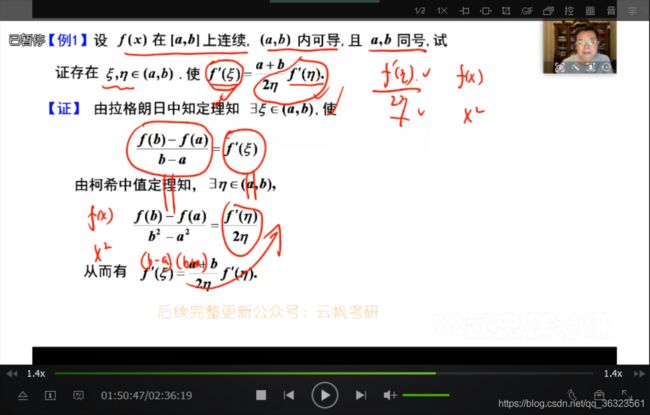
【例】
按照汤老的说法,基于两个不同的中值将表达式分为复杂和简单部分,
简单部分一般是仅含有一阶导的部分,这部分通常可利用拉格朗日中值定理进行表达式的替换;
复杂的部分基于不同的情况使用不同的中值定理,对于本题,复杂部分为导函数之比的形式,则固定用柯西中值定理。
基于简单复杂部分分为两边
【例】
【例】
case2、要求高(要求两中值不同)
该类题型一般为中间点分割两区域,两区域分别用中值定理
// 难点考查为不给定分点,自己分析找出(注意例题中找出分点的思想方法)
逆推法 找分点
【例4】
本题为要求不同的两个中值,故不能在同一区间用中值定理,需用分点分开区间用拉格朗日
主要考查分点的选取
// 本题是早年真题,第一问中给出分点提示,但今后出题可能将不再给提示,那么如何找出分点,见下例
【例5】
利用逆推法求出中间点
类型三、n阶导数相关
// 高阶导数问题往往离不开泰勒
// 注意泰勒公式证明题中的另一种思想:多项式拟合
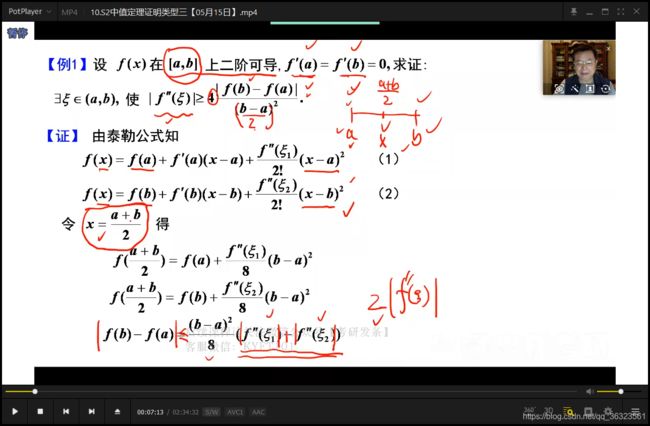
【例1】
① 建立高阶导与函数之间的关系用泰勒公式;
② 在已知信息多的点处使用泰勒公式;
③ x取合适的值,此处表示距离a、b位置相等的点,即a、b的中点。
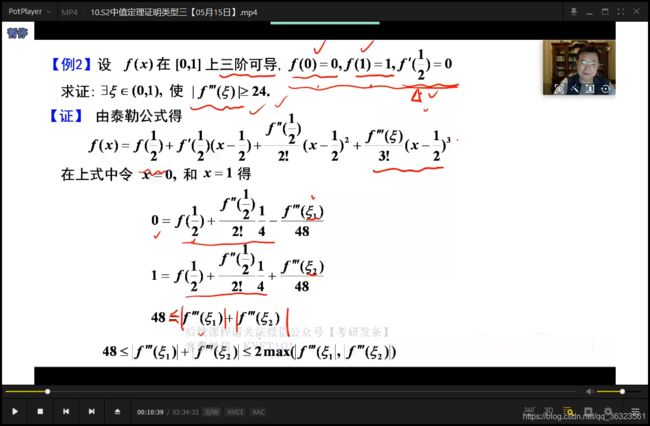
【例2】
{补充}:在选择在哪一点使用泰勒中值定理时,一般选择已知信息多的点;
当条件所给的点的信息一样多,一般选择导数阶数高的点使用泰勒中值定理。
【例3】
{补充}:新的思想方法:多项式拟合
待证结果为几次,就证明几次多项式
多项式拟合,
构造一个多项式,要求和原来的函数有着相同的条件,构造的多项式的次数取决于待证结论中导数的阶数
【补充】泰勒公式证明题中的另一种思想:多项式拟合
待整理
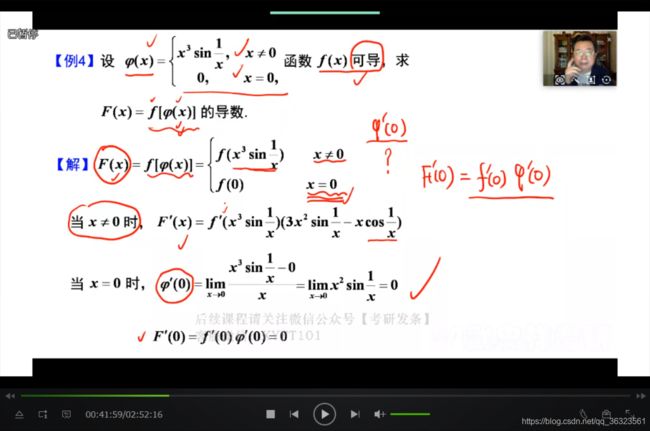
* 补充题型 分段函数求导
连续函数求导直接使用求导公式。
一点处的导数值需要用导数定义来求导。
求分段函数在分段点处的导数时,一般使用定义法求;但是当函数在分段点处连续的时候,可有其他方法,如下
若
(1) f ( x ) f(x) f(x) 在 x 0 x_0 x0 处连续;
(2) f ( x ) f(x) f(x) 在 x 0 x_0 x0 的某空心邻域内可导;
(3) lim x → x 0 f ′ ( x ) \lim_{x\to x_0}{f'(x)} limx→x0f′(x) 存在。
则, f ′ ( x 0 ) = lim x → x 0 f ′ ( x ) f'(x_0)=\lim_{x\to x_0}{f'(x)} f′(x0)=limx→x0f′(x)