Pytorch基础教程（4）：入门——神经网络

softmax的基本概念

• 分类问题：
  • 一个简单的图像分类问题，输入图像的高和宽均为2像素，色彩为灰度。
  • 图像中的4像素分别是$x_1$，$x_2$，$x_3$，$x_4$。
  • 假设真实标签为狗、猫或者鸡，这些标签对应的离散值为$y_1$，$y_2$，$y_3$。
  • 我们通常使用离散的数值来表示类别，例如$y_1=1$，$y_2=2$，$y_3=3$。
• 权重矢量
  • $o_1=x_1{w}_{11}+x_2{w}_{21}+x_3{w}_{31}+x_4{w}_{41}+b_1$
  • $o_2=x_1{w}_{12}+x_2{w}_{22}+x_3{w}_{32}+x_4{w}_{42}+b_2$
  • $o_3=x_1{w}_{13}+x_2{w}_{23}+x_3{w}_{33}+x_4{w}_{43}+b_3$
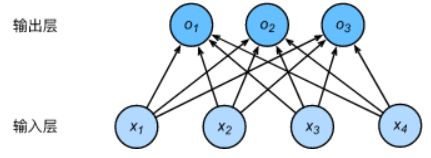
• 神经网络图
  • 下图用神经网络图描绘了上面的计算。softmax回归同线性回归一样，也是一个单层神经网络。由于每个输出$o_1$，$o_2$，$o_3$的计算都要依赖于所有的输入$x_1$，$x_2$，$x_3$，$x_4$，softmax回归的输出层也是一个全连接层。
    既然分类问题需要得到离散的预测输出，一个简单的办法是将输出值当作预测类别是的置信度，并将值最大的输出所对应的类作为预测输出，即 输出$\arg {\max }_i{o}_i$。例如，如果$o_1$，$o_2$，$o_3$分别是0.1,10,0.1,由于$o_2$最大，那么预测类别为2，其代表猫。
• 输出问题
  • 直接使用输出层的输出有两个问题：
  • 一方面，由于输出层的输出值的范围不确定，我们难以直观上判断这些值的意义。例如，刚才举的例子中的输出值10表示“很置信”图像类别为猫，因为输出值是其他两类的输出值的100倍。但如果$o_1=o_3=10^3$，那么输出值10却又表示图像类别为猫的概率很低。
  • 另一方面，由于真实标签是离散值，这些离散值与不确定范围的输出值之间的误差难以衡量。
• softmax运算符解决了以上两个问题。它通过下式将输出值变换成值为正且和为1的概率分布：
  • ${\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3=softmax(o_1,o_2,o_3)$
  • 其中，${\hat{y}}_1=\frac{exp(o_1)}{{\sum }_{i=1}^{3}exp(o_i)}$，${\hat{y}}_2=\frac{exp(o_2)}{{\sum }_{i=1}^{3}exp(o_i)}$，${\hat{y}}_3=\frac{exp(o_3)}{{\sum }_{i=1}^{3}exp(o_i)}$
  • 容易看出${\hat{y}}_1+{\hat{y}}_2+{\hat{y}}_3=1$且$0\le {\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3\le 1$，因此${\hat{y}}_1$, ${\hat{y}}_2$, ${\hat{y}}_3$是一个合法的概率分布。这时候，如果${\hat{y}}_2=0.8$，不管${\hat{y}}_1$和${\hat{y}}_3$的值是多少，我们都知道图像类别为猫的概率为80%。此外，我们注意到$\arg {\max }_i{o}_i=\arg {\max }_i{\hat{y}}_i$。因此softmax运算不改变预测类别输出。
• 计算效率
  • 单样本矢量计算表达式
  • 为了提高计算效率，我们可以将单样本分类通过矢量计算来表达。在上面的图像分类问题中，假设softmax回归的权重和偏差参数分别为
    • $W=\left[\begin{array}{ccc}{w}_{11}& w_{12}& w_{13}\\ w_{21}& w_{22}& w_{23}\\ w_{31}& w_{32}& w_{33}\\ w_{41}& w_{42}& w_{43}\end{array}\right]$，$b=[b_1,b_2,b_3]$
    • 设高和宽分别为2个像素的图像样本的特征为：$x^{(i)}=[x_1^{(i)}{x}_2^{(i)}{x}_3^{(i)}{x}_4^{(i)}]$
    • 输出层的输出为：$o^{(i)}=[o_1^{(i)}{o}_2^{(i)}{o}_3^{(i)}]$
    • 预测为狗、猫或鸡的概率分布为：${\hat{y}}^{(i)}=[{\hat{y}}_1^{(i)}{\hat{y}}_2^{(i)}{\hat{y}}_3^{(i)}]$
    • softmax回归对样本分类的矢量计算表达式为：KaTeX parse error: No such environment: align at position 7: \begin{̲a̲l̲i̲g̲n̲}̲ o^{(i)}=x^{(i)…
  • 小批量矢量计算表达式
  • 为了进一步提升计算效率，我们通常对小批量数据做矢量计算。广义上讲，给定一个小批量样本，其批量大小为$n$，输入个数（特征数）为$d$，输出个数（类别数）为$q$。设批量特征为$X\in R^{n\times d}$。假设softmax回归的权重和偏差参数分别为$W\in R^{d\times q}$和$b\in R^{1\times q}$。softmax回归的矢量计算表达式为：KaTeX parse error: No such environment: align at position 7: \begin{̲a̲l̲i̲g̲n̲}̲ O=XW+b\\ \hat …
• 其中的加法运算使用了广播机制，$O,\hat{Y}\in R^{n\times q}$且这两个矩阵的第$i$行分别为样本$i$的输出$o^{(i)}$和概率分布${\hat{y}}^{(i)}$。

交叉熵损失函数

• 对于样本，我们构造向量$y^{(i)}\in R^q$，使其第$y^{(i)}$（样本$i$类别的离散数值）个元素为1，其余为0。这样我们的训练目标可以设为使预测概率分布${\hat{y}}^{(i)}$尽可能接近真实的标签概率分布$y^{(i)}$。
• 平方损失估计：$Loss=|{\hat{y}}^{(i)}-y^{(i)}{|}^2/2$
• 然而，想要预测分类结果正确，我们其实并不需要预测概率完全等于标签概率。例如，在图像分类的例子里，如果$y^{(i)}=3$，那么我们只需要${\hat{y}}_3^{(i)}$比其他两个预测值${\hat{y}}_1^{(i)}$和${\hat{y}}_2^{(i)}$大就行了。即使${\hat{y}}_3^{(i)}$值为0.6，不管其他两个预测值为多少，类别预测均正确。而平方损失则过于严格，例如${\hat{y}}_1^{(i)}={\hat{y}}_2^{(i)}=0.2$比${\hat{y}}_1^{(i)}=0,{\hat{y}}_2^{(i)}=0.4$的损失要小很多，虽然两者都有同样正确的分类预测结果。
• 改善上述问题的一个方法是使用更合适衡量两个概率分布差异的测量函数。其中，交叉熵是一个常用的衡量方法：$H\left(y^{(i)},{\hat{y}}^{(i)}\right)=-{\sum }_{j=1}^q{y}_j^{(i)}\log {\hat{y}}_j^{(i)}$
• 假设训练数据集的样本数为，交叉熵损失函数定义为：$L(\theta )=\frac{1}{n}{\sum }_{i=1}^{n}H\left(y^{(i)},{\hat{y}}^{(i)}\right)$
• 其中$\theta$代表模型参数。同样地，如果每个样本只有一个标签，那么交叉熵损失可以简写成$L(\theta )=-(1/n){\sum }_{i=1}^n\log {\hat{y}}_{y^{(i)}}^{(i)}$。从另一个角度来看，我们知道最小化$L(\theta )$等价于最大化$exp(-nL(\theta ))={\prod }_{i=1}^n{\hat{y}}_{y^{(i)}}^{(i)}$，即最小化交叉熵损失函数等价于最大化训练数据集所有标签类别的联合预测概率。

模型训练和预测

• 在训练好softmax回归模型后，给定任一样本特征，就可以预测每个输出类别的概率。通常，我们把预测概率最大的类别作为输出类别。如果它与真实类别（标签）一致，说明这次预测是正确的。

获取数据集

Label	0	1	2	3	4	5	6	7	8	9
Description	T-shirt	Trouser	Pullover	Dress	Coat	Sandal	Shirt	Sneaker	Bag	Ankle boot

import time
import torch
import numpy as np
from torch import nn, optim
import torchvision

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

###################fashion mnist数据集加载######################
def load_data_fashion_mnist(batch_size, resize=None, root='./Datasets/FashionMNIST'):
    """Download the fashion mnist dataset and then load into memory."""
    trans = []
    if resize:
        trans.append(torchvision.transforms.Resize(size=resize))
    trans.append(torchvision.transforms.ToTensor())
    
    transform = torchvision.transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True, transform=transform)
    mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True, transform=transform)
    train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True)
    test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False)

    return train_iter, test_iter
#################################################################
batch_size = 32
train_iter, test_iter = load_data_fashion_mnist(batch_size)

定义网络结构

num_inputs = 784
num_outputs = 10

class LinearNet(nn.Module):
    def __init__(self, num_inputs, num_outputs):
        super(LinearNet, self).__init__()
        self.linear = nn.Linear(num_inputs, num_outputs)
    def forward(self, x): # x 的形状: (batch, 1, 28, 28)
        y = self.linear(x.view(x.shape[0], -1))
        return y

class FlattenLayer(nn.Module):
    def __init__(self):
        super(FlattenLayer, self).__init__()
    def forward(self, x): # x 的形状: (batch, *, *, ...)
        return x.view(x.shape[0], -1)

from collections import OrderedDict
net = nn.Sequential(
        OrderedDict([
           ('flatten', FlattenLayer()),
           ('linear', nn.Linear(num_inputs, num_outputs))])
        )
print(net)

Sequential(
(flatten): FlattenLayer()
(linear): Linear(in_features=784, out_features=10, bias=True)
)

初始化模型参数

nn.init.normal_(net.linear.weight, mean=0, std=0.01)
nn.init.constant_(net.linear.bias, val=0)

Parameter containing:
tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], requires_grad=True)

定义损失函数

loss = nn.CrossEntropyLoss()

定义优化函数

def execute(sql):
    from tqdm.notebook import tqdm
    from time import sleep
    from IPython.display import display, HTML, clear_output
    import pandas as pd

    global _sql_execute_result, o

    if "o" not in globals():
        print("Please run odps configuration cell first")
        return

    if "_sql_execute_result" not in globals():
        _sql_execute_result = {}

    bar = tqdm(total=1, desc='Preparing sql query')
    progress = None

    instance = o.run_sql(sql)

    bar.update(1)

    display(
        HTML(
            f'
Open LogView to checkout details
'
        )
    )

    finished_last_loop = 0

    while not instance.is_terminated():
        task_progress = instance.get_task_progress(instance.get_task_names())
        stages = task_progress.stages
        finished = sum(map(lambda x: x.terminated_workers, stages))
        total = sum(map(lambda x: x.total_workers, stages))
        if progress:
            if len(stages) == 0:
                progress.update(total)
            else:
                progress.update(finished - finished_last_loop)
                finished_last_loop = finished
        elif not progress and len(stages) == 0:
            continue
        else:
            progress = tqdm(total=total, desc='executing sql query')
            progress.update(finished - finished_last_loop)
            finished_last_loop = finished
        sleep(1)
    print('The data is being formatted. If the amount of data is large, it will take a while')
    df = instance.open_reader().to_pandas()

    result_key = len(_sql_execute_result.keys())
    _sql_execute_result[result_key] = df

    pd.options.display.html.table_schema = True
    pd.options.display.max_rows = None
    clear_output()
    print("you can find execute result in global variable: _sql_execute_result[{}]".format(result_key))

    return df

execute('''''')

定义准确率

def accuracy(y_hat, y):
    return (y_hat.argmax(dim=1) == y).float().mean().item()

def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for X, y in data_iter:
        acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
        n += y.shape[0]
    return acc_sum / n

训练

num_epochs = 5

def train_ch(net, train_iter, test_iter, loss, num_epochs, batch_size,
              params=None, lr=None, optimizer=None):
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            y_hat = net(X)
            l = loss(y_hat, y).sum()
            
            # 梯度清零
            if optimizer is not None:
                optimizer.zero_grad()
            elif params is not None and params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()
            
            l.backward()
            optimizer.step() 
            
            train_l_sum += l.item()
            train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
            n += y.shape[0]
        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
              % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))

train_ch(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer)

epoch 1, loss 0.0185, train acc 0.799, test acc 0.822

练习题

选择题：

1. softmax([100, 101, 102])的结果等于以下的哪一项
   • A.softmax([10.0, 10.1, 10.2])
   • B.softmax([-100, -101, -102])
   • C.softmax([-2, -1, 0])
   • D.softmax([1000, 1010, 1020])

答案：

1. C
   

通过将网络结构修改成上述的卷积形式。