3D 可视化入门:渲染管线原理与实践
前端技术深度复盘, 今天也要博学一下~
一、引子
玩 3D 游戏的时候,有没有想过这些 3D 物体是怎么渲染出来的?其中的动画是怎么做的?为什么会出现穿模、阴影不对、镜子照不出主角的情况?要想解答这些问题,就要了解实时渲染。其中最基础的,就是渲染管线。
「渲染管线」(rendering pipeline),又称图形学管线(graphics pipeline),是计算机将 3D 模型渲染至 2D 屏幕上的一个概念模型。
渲染管线一般仅指 3D 多边形渲染的渲染流程,与 光线追踪(ray tracing) 等不同。光线追踪是根据光路可逆原理,从视点发出光线,当其碰撞到物体表面时,根据表面材质计算出对应的颜色和光强,并继续计算反射与折射等,最终追溯到光源或无贡献点。而 3D 多边形渲染,则是从物体发出光线,并最终落到视点。
渲染管线一般分为 4 个部分,应用(Application)、几何处理(Geometry Processing)、光栅化(Rasterization) 和 像素处理(Pixel Processing)。不同资料、不同实现可能有不同的划分方法,但总体的流程是相似的。

《Real-time Rendering, 4th》的渲染管线
本文组织方式以 「Real-time Rendering, 4th」 提到的渲染管线为主,为了解决具体问题,以 OpenGL、WebGPU 中渲染流程以及 three.js 中的应用举例。
二、应用阶段
试想我们在玩的 3D 游戏中,有各种各样的 模型、纹理、运动、光线、碰撞检测、生物AI、动画 等等。但对于 GPU 来说,它只关心 「图元(primitives)」。
图元是基本可绘制单元,一般指 「点、线段 和 三角形」,其本质上是顶点的集合。比如线段就是两个顶点、三角形就是三个顶点。一般来说,图元最多只有三角形,因为它们总是有相同的顶点数,而且三个顶点可以确定一个平面,后续可以方便地将其视为一个二维平面来处理。如果有四个点,就需要额外的方法保证其在同一平面,且不产生凹多边形。

没错,即使是球面,也可以用三角形表示
因此,在进入 GPU 渲染前,需要完成 运动、动画、碰撞、AI 等相应的运算,并将要渲染的内容转换为图元。最终将一系列图元、指令、纹理、以及各种参数上传到 GPU 中。
示例:https://threejs.org/docs/index.html?q=Geometry#api/en/geometries/BoxGeometry

2.1 图元拓扑
示例:https://06wj.github.io/WebGPU-Playground/#/Samples/ClickedPoints
在画布上点击鼠标时,会在画布对应位置绘制 1 个像素点(由于 1 个像素点很难看到,例子中将画布缩放了 10 倍,因此看起来会比较模糊)。

每点一次鼠标,就在图元数组中添加一个顶点,完成整个渲染的流程后,在画布上绘制出了一个白色的点。

那么怎么画线和三角形呢?在 WebGPU 中,通过 pipeline 的 primitive.topology,可以指定顶点的拓扑方式,目前有以下 5 种。其他的实现也有类似的配置方法。
type GPUPrimitiveTopology =
| "point-list" // 点
| "line-list" // 线
| "line-strip" // 线条带
| "triangle-list" // 三角形
| "triangle-strip"; // 三角形条带
// 如果是 -strip,还需要指定 stripIndexFormat。什么是三角形条带?

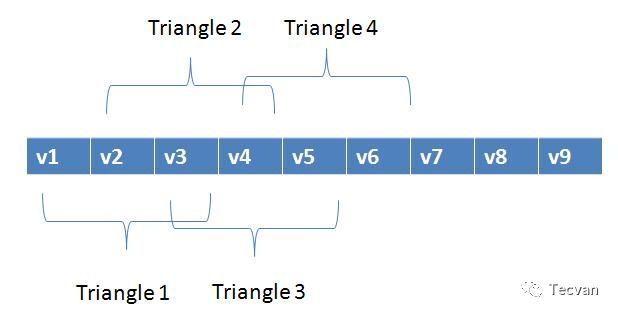
一般来说,我们的模型都是由连续的三角形组成的,会有多个三角形共用顶点的情况。如果用顶点表示三角形 (v1, v3, v2) (v2, v3, v4) (v3, v5, v4)... 绘制 n 个三角形就需要 3n 个顶点,其中会有很多重复的顶点。如果共用这些顶点,绘制 n 个三角形就只需要 n + 2 个顶点。因此,我们在描述顶点时,省略这些重复的顶点,这就是条带。
但要注意三角形顶点是有顺序的,三角形顶点顺序是顺时针(cw)还是逆时针(ccw),决定构成的整个三角面是面朝相机还是背朝相机。这个信息很重要,后续步骤可以将背朝相机的面剔除。比如上面的条带,如果后续步骤中如果以 (v1, v2, v3) 顺时针为正面,那么下一个三角形的绘制应该是 (v2, v4, v3), (v3, v4, v5),(v4, v6, v5)...

要想绘制一个三角形条带,顶点顺序应该是这样的
在 WebGPU 中,默认是逆时针顺序,也可由 GPUFrontFace 配置正面是顺时针还是逆时针。
示例:https://06wj.github.io/WebGPU-Playground/#/Samples/HelloTriangle
这个例子中的三角面是逆时针的,没有开启背面剔除。你可以尝试开启背面剔除,并将其调整为顺时针观察它是否仍能渲染。
// 实践解答
const pipeline = device.createRenderPipeline({
vertex: {
// ...
},
fragment: {
// ...
},
primitive:{
topology: 'triangle-list',
cullMode: 'back', // 'back' | 'front' | 'none'
frontFace: 'cw', // 'cw' | 'ccw'
},
});将图元及其他信息上传至 GPU 后,接下来就交由 GPU 进行处理。
三、几何处理阶段
到这里,我们至少拿到了一些图元。几何处理阶段分为以下 4 个功能阶段,对图元进行处理,最终得到其在屏幕空间的坐标。

3.1 顶点着色 - Vertex Shading
在不考虑拓扑方式的情况下,也就是一些顶点。这一阶段,我们对顶点进行处理。
顶点着色是通过目前已有的信息,给这些顶点附加一些属性(比如颜色、材质、法线)或者做一些修改(比如调整位置、丢弃)。这一阶段最重要的,是确定顶点在画布上的位置,位置也是顶点着色器唯一必要的输出。
我们继续看刚刚的 WebGPU 的例子,顶点着色器唯一做的就只是将 2 维数组 [x, y] 转换为只有 位置 (x, y, z=0.0, w=1.0) 向量的最简单的顶点。
const vs = `
// ...
[[stage(vertex)]]
fn main([[location(0)]] a_position : vec2) -> VertexOutput {
var output : VertexOutput;
output.position = vec4(a_position, 0.0, 1.0);
return output;
}
`; 顶点坐标在齐次坐标系中,因此位置虽是 3 维向量,却需要用 4 维向量来表示。后续在投影时会详细讲解。
3.1.1 坐标变换(Coordinate Transform)
画一个 2D 三角形,确定顶点的位置很容易。但实际场景中,物体是 3D 的,处在 3D 的场景中,我们要进行一系列坐标变换才能确定顶点在屏幕上的位置。
前置知识:对于任意二维或三维空间上的点,我们都可以通过应用矩阵变换的方式,将其进行仿射(affine)变换,比如平移、缩放、拉伸 和 旋转。因此,在这个阶段,我们就通过一步步的矩阵坐标变换,来最终确定顶点在屏幕上的位置。
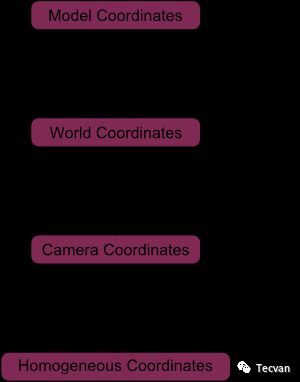
MVP(Model-View-Projection) 矩阵坐标变换流程
虽然通常三种变换会同时应用,但投影矩阵与其他两种矩阵不同,因为透视投影不是仿射的,严格来说,它「几乎」不能被正交矩阵变换表示。
3.1.1.1 模型矩阵
以最基础的立方体模型为例,首先要有立方体各个顶点的相对坐标。我们将其称为 模型坐标(model coordinates)。三个坐标轴的原点位于模型中心,换句话说,如果一个顶点在模型的中心,它的坐标应该是 (0, 0, 0)。
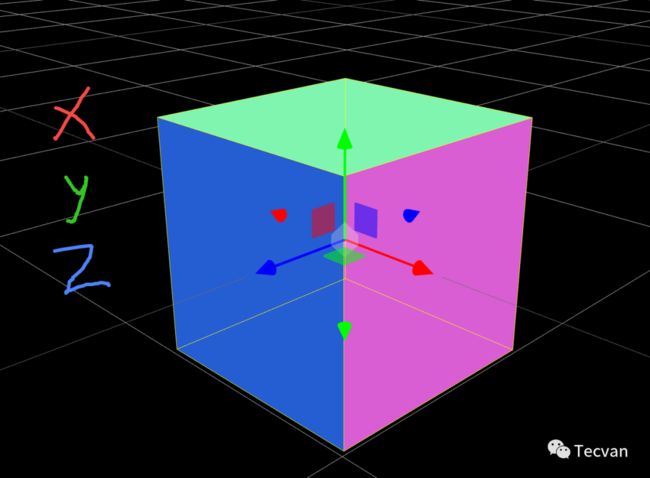
在 3D Canvas 中,坐标通常是右手系,坐标轴的方向如图示
一个场景中可能有多个相同模型,这些模型可以有各自不同的旋转、平移、缩放变换,因此需要对它们应用模型矩阵(model matrix),将其坐标变换为世界坐标(world coordinates),并放置在场景(世界空间, world space)中。

这些都是的 1x1x1 的立方体,通过模型矩阵变换,让它们在世界空间表现不同
3.1.1.2 视图矩阵
我们在不同位置、眼睛看向不同角度时,眼前的物体是不同的,这说明 "我们" 的位置和朝向也很重要。在 3D 场景中,"我们" 就是 「相机(camera)」。因此,需要通过应用视图矩阵(view matrix),将 以世界为原点的模型坐标 变换为 以相机为原点的相机坐标(camera coordinates)。

3.1.1.3 投影矩阵
投影矩阵有两种。我们人眼看到的物体总是 近大远小,顶点的位置还应当与相机的距离有关,平行线在无限远甚至还会相交,这称为 透视投影(perspective projection)。它仍然可以用一个 4x4 的矩阵实现。与透视投影不同,正交投影(orthographic projection)下,物体在投影平面上的大小与其相对距离远近没有关系。在建筑蓝图绘制和设计中常会用到正交投影,以确保物体尺寸和相互间角度不会变。

3.1.2 光照,动画与纹理坐标(UV)变换
这一部分作为顶点着色的可选输出,会在渲染管线主流程后讲解。
因为顶点数量一般远远小于像素点数量,因此为了提高性能,可以在顶点阶段进行光照计算、着色等,但这样精确度通常较低。随着 GPU 算力的提高,这些一般在后续阶段,对每个像素进行处理。顶点着色器倾向于只输出顶点相关信息。
3.1.3 曲面细分(Tessellation)*
顶点越多,三角形就越多,就越能表达不同的平面,就越能支持更多的细节。曲面细分通过一系列的算法,向原始图元内添加更多顶点,以形成更精细的模型。

同时,因为它添加了更多的顶点,也为后续移位贴图(displacement map)提供了更多操作空间。
示例:https://threejs.org/docs/index.html#api/en/geometries/SphereGeometry
这个例子通过调整对应参数,模拟曲面细分,可以看到当数值较低时,看起来就不太球了(在 WebGL 中,曲面细分不是可编程阶段)。

3.1.4 几何着色(Geometry Shading)*
与曲面细分在图元内部添加顶点的操作不同,它可以通过丢弃顶点或在图元外额外添加顶点,将原始图元转换为 0 个或多个新图元。

将三角形变为更多三角形,或将线段变为折线
有一种说法是,它常用来实现大量粒子的渲染。比如,每个粒子只用一个顶点,在此阶段,将其拓展为不同形状的多边形或丢弃,通过纹理贴图的方式来渲染大量粒子。
但实际上,这一着色器通常性能很差,大多数人甚至大多数 GPU 厂商都认为,应该避免在实际中使用。在 WebGL 和 WebGPU 中,几何着色器均不可用。
3.2 投影 - Projection
投影分平行投影和透视投影两类。在 3D 渲染中一般使用正交投影和透视投影。
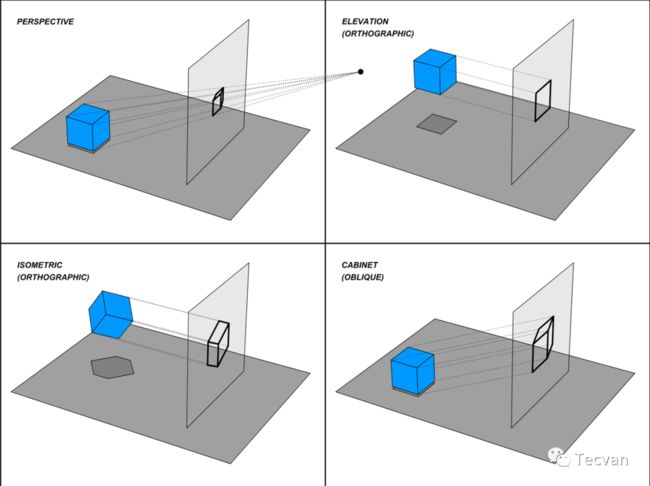
透视投影,正投影,等轴测投影,斜投影
示例:https://threejs.org/examples/?q=camera#webgl_camera
通过切换不同的相机,查看透视投影与正交投影的区别。
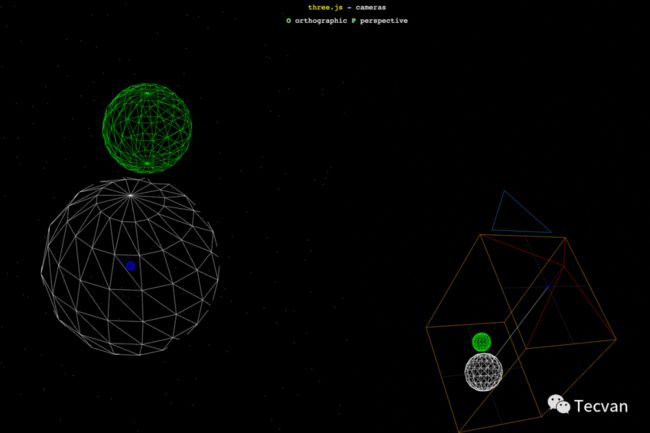
3.2.1 正交投影(Orthographic Projection)
正交投影是平行投影的一种,这类投影最大的特点是 没有近大远小,平行线投影后还是平行的。
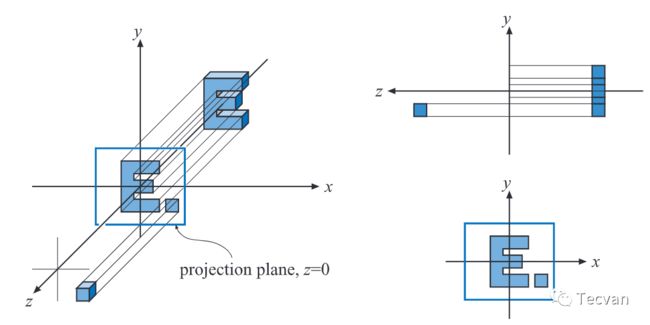
它还细分为正投影,即绘制物体三视图的投影,和轴侧投影,能同时看到多个面的投影。轴测投影又分为对等轴测投影、正二测投影和正三测投影,分别表示三坐标轴缩放比例是否相同(或者说夹角是否相等)等轴测投影都相同,正二测有2个轴相同,正三测都不同。
在 3D 渲染中,正交投影可配置参数有 6 个,分别为六面体的左右上下远近。最终投影矩阵如下:
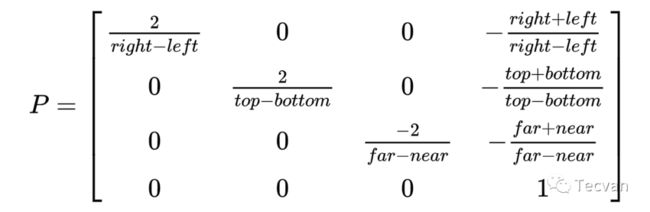
3.2.2 透视投影(Perspective projection)
透视投影的特点是,越远的物体看起来越小,平行线最终会交于一点。
在 3D 渲染中,透视投影的可配置参数有 4 个,分别为 fov、视锥面的长宽比、近平面和远平面。最终的投影矩阵如下(OpenGL):

其中

运算后 (x, y, z, w) 的 w 可能不是 1,硬件会自动对其进行处理。
示例:https://06wj.github.io/WebGPU-Playground/#/Samples/HelloTriangle
在这个示例中,如果输出的顶点坐标 w 不是 1.0,稍微修改 w 的值,三角形会发生什么?为什么?这是否解释了即使透视投影不是仿射的,也能用矩阵变换来表示?
const vs = `
// ...
[[stage(vertex)]]
fn main([[location(0)]] a_position : vec2) -> VertexOutput {
var output : VertexOutput;
output.position = vec4(a_position, 0.0, 1.0); // 这里是 w
return output;
}
`; | w = 3.0 | w = 0.9 |
|---|---|
 |
 |
3.3 剪裁 - Clipping
剪裁是将不需要显示在屏幕上的多边形剪裁掉,以减少后续需要处理的数据,提高性能。剪裁分为 2 种:2D 剪裁 和 3D 剪裁。
2D 剪裁会移除不在可视平面或者视窗的多边形。对于一半在一半不在的多边形,则会添加顶点。

3D 剪裁分为多种,一些剪裁在渲染流程中可以分别启用或禁用。
视锥体剪裁:移除不在视锥体范围内以及近剪切面内、远剪切面外的多边形。

背面剔除:根据顶点顺序,移除背面(或正面)朝向我们的多边形。
遮挡剔除:如果多边形被另一个多边形完全遮挡,则剔除。
(在之前的实践中,我们尝试过启用背面剔除)
3.4 屏幕映射 - Screen Mapping
经过上述一系列处理后,我们会得到一个非常方的单位立方体,其中 (x, y, z) 都是 [-1, 1]。现在,我们需要将标准化的设备坐标(Normalized device coordinate) 转换为 屏幕坐标,比如 x 从 [-1, 1] => [0, 1024), y 从 [-1, 1] => [0, 768),也有一些实现会将 z 映射到 [0, 1]。
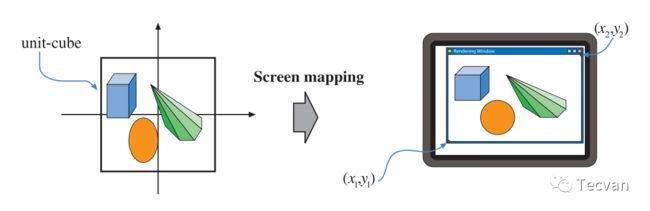
3.5 几何阶段回顾
回顾一下整个几何处理阶段,它的输入是一系列 图元,然后经过顶点着色(必选,至少产出顶点的位置)后,进行曲面细分和几何着色,让图元更加精细,最后,通过剪裁和屏幕映射,得到所有需要绘制的顶点的窗口坐标,以及顶点着色器为顶点添加的其他信息(如颜色、法向量、纹理UV坐标等)。
四、光栅化阶段
光栅化也称为扫描转换(scan conversion)。虽然我们的顶点连线和三角形都是连续的,但屏幕是由像素组成的,因此我们需要将我们的图元离散化为片元(fragment, 覆盖的像素点的集合),以便于后续的像素处理及显示。经过光栅化后,我们可以确定哪些像素属于哪些图元,得到对应的片元。
 |
 |
这一阶段主要包括两个过程:图元装配与三角形遍历。
4.1 三角形组装(图元装配) - triangle setup (primitive assembly)
之前我们说图元是三角形,但实际上只是一些顶点的位置与拓扑数据。在这一阶段,我们会真正将这些点坐标连成三角形或线段(通过差值,求出对应的位置、颜色、法线方程等),并提供给下一步。
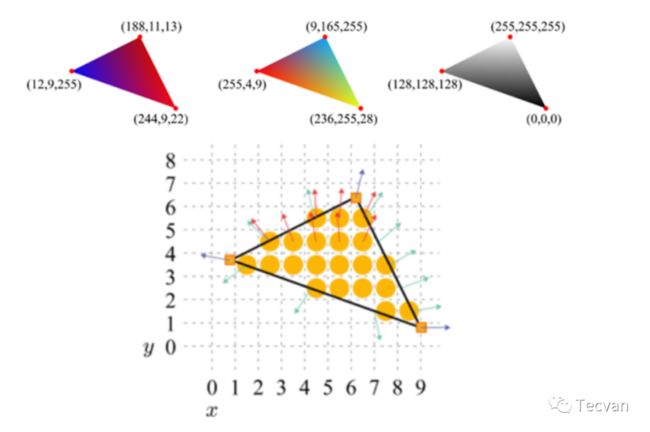
对颜色和法线进行差值,可参考后文 多边形着色
4.2 三角形遍历 - triangle traversal
这一部分,通过各种算法,确定这些图元会覆盖哪些像素,并确保没有一个像素被多个三角形覆盖(节省渲染资源,并避免渲染顺序对渲染结果产生影响),得到该图元对应的片元。
4.2.1 绘制边界
「数字微分画线法(Digital Differential Analyzer, DDA)」
设线段两点坐标为 (x1, y1), (x2, y2),则:
假设斜率 m <= 1,则令 x = x1,x 坐标每增加 1,y 坐标增加 m,由于 m 可能是小数,对 y 取整后绘制。
假设斜率 m > 1,则交换 x 与 y。

如果 m > 1,会有大量网格无法绘制,交换 xy 即可解决
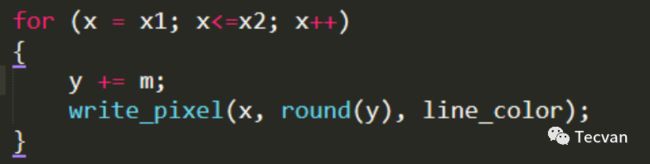
但是这一算法涉及浮点数运算,性能比较差。
「Bresenham 算法」
这一算法只需进行整数加减及位运算,避免了浮点运算,作为 DDA 的优化,可以在此详细了解:https://zhuanlan.zhihu.com/p/74990578
「抗锯齿」
一种思路:将一个像素拆分为更多的区域,并根据扫过的像素点进行颜色混合。

4.2.2 填充三角形
这里最常见的是使用扫描线填充法。

每扫到一条边,则 +1,如果是奇数,则填充扫描到的像素点。要注意的是,如果扫描到了顶点,需要用相邻的顶点是否在扫描线两侧来判断是不是进入或离开多边形。这个算法也可以进行优化。
五、像素处理阶段 - Pixel Processing
到此为止,我们得到了所有片元信息。接下来,我们需要处理这些片元。
5.1 像素着色(片元着色)* - Pixel Shading(Fragment Shading)
这一部分,我们需要计算出每一个像素的颜色。
示例:https://06wj.github.io/WebGPU-Playground/#/Samples/HelloTriangle
示例中,片元着色器只输出了一个
vec4代表颜色。如果把这个三角形改成绿色,应该怎么做?第 4 个值是用来控制什么?修改为什么没效果?
const fs = `
[[stage(fragment)]]
fn main() -> [[location(0)]] vec4 {
return vec4(1.0, 0.0, 0.0, 1.0);
}
`; 在真实场景中,片元着色是非常复杂的,包括物体的材质、高光、阴影、贴图、反射... 是一个大坑。我们将在后续介绍。
5.2 像素合并 - Pixel Merging
到此,我们得到了每个片元对应的像素颜色,接下来需要将所有片元的颜色合并。此时,很可能有一些三角形彼此遮挡,因此需要一定的算法来决定如何绘制。绝大多数硬件都通过 深度缓冲(z-buffer) 算法实现的。在绘制时,存储要绘制的像素的深度,当准备覆盖它时,先测试将要绘制的像素深度是否小于已经绘制的深度,小于则覆盖并更新深度信息,否则保持不变。
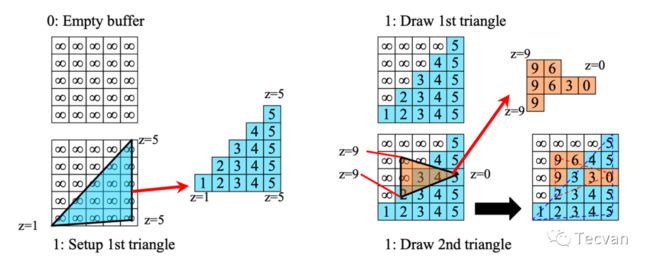
但是深度缓冲算法只有渲染、不渲染两种结果,它没办法渲染半透明物体。
我们的渲染管线到这里就完成了。
六、总结
等等!怎么就总结了?学了这个渲染流程,好像什么问题都没解答啊!怎么光照,怎么反光,怎么贴图,怎么骨骼动画?好像还是什么也不知道... 我只记住了 顶点着色阶段输出顶点位置,片元着色阶段输出颜色,然后就没有然后了...
没关系,我们先回顾下:

顶点着色:通过一系列坐标变换确定顶点的位置,也可以提供一些额外信息。
曲面细分:在图元内部加顶点,使图元更加精细化,看起来更细腻,并便于置换贴图。
几何着色:可以添加或移除图元,一般不用。
剪裁:移除不会被渲染的部分以提高性能和渲染精细度。
屏幕映射:将坐标从单位立方体转换为屏幕坐标。
图元装配和遍历:确定三角形对应的像素。
像素着色:确定每个像素点的颜色。
像素合并:将所有片元的像素合并。
这些步骤完成后,经过一系列测试和混合,终于可以显示在屏幕上了。

接下来,我们将尝试解答更多问题。
七、渲染实践
7.1 动画与简单着色
说到动画,应该是改变顶点的位置,改变位置,那就是应用变换矩阵。因此,我们可以给顶点着色器提供额外的参数,并通过 requestAnimationFrame 改变它的值。
示例:https://06wj.github.io/WebGPU-Playground/#/Samples/RotatingTriangle
示例中,如果不使用
Hilo``3d.Matrix3(),是否可以创建一个可以旋转的动画矩阵?提示:mat3x3是向 16 字节对齐的数据结构,因此数组中有 12 个元素,但第 4、8、12 个元素无意义。
// 实践的解
let rotateAngle = 1;
function getModelMatrix(){
let matrix = CSSStyleValue.parse('transform', `rotate(${rotateAngle++}deg)`).toMatrix();
const { a, b, c, d, e, f } = matrix;
modelMatrixData.set([a, c, e, b, d, f, 0, 0, 1]);
modelMatrixData.copyWithin(8, 6, 9);
modelMatrixData.copyWithin(4, 3, 6);
return modelMatrixData;
}说到着色,应该是修改片元着色器的输出。如果我想让三角形拥有不同颜色,应该怎么做?
示例:https://06wj.github.io/WebGPU-Playground/#/Samples/MultiAttributeColor
示例中,我们可以在顶点着色阶段,提供颜色信息,并在片元着色阶段直接使用。

诶?我们只给 3 个顶点分别提供了 红、绿、蓝 三种颜色,为什么最终输出结果是彩色的?这是因为,顶点着色器的输出默认会差值后送给片元着色器。如果不希望被差值,我们可以将差值 interpolate 方式设置为 flat。
const vs = `
struct VertexOutput {
[[builtin(position)]] position : vec4;
[[location(0), interpolate(flat)]] v_color : vec3;
};
// ...
`;
const fs = `
[[stage(fragment)]]
fn main([[location(0), interpolate(flat)]] v_color: vec3) -> [[location(0)]] vec4 {
return vec4(v_color, 1.0);
}
`; 设置后,整个三角形都是红色,因为这个面的颜色将取决于 代表顶点。
接下来,我们将在场景中引入 光。
7.2 光
渲染 3D 场景最复杂的部分就是模拟光和光的相互作用,一方面是要尽可能真实,一方面,性能又要尽可能好。这一部分,分为光源、光的相互作用、光照模型、着色和光效。
7.2.1 光源
我们以 ThreeJS 的光源为例,介绍几种常见的光源:
https://threejs.org/docs/index.html?q=Light#api/en/lights/AmbientLight
环境光源 AmbientLight:它会均匀地照亮场景中的所有物体。

平行光源 DirectionalLight:发射有方向的平行光线,一般用来模拟太阳光。

半球光源 HemisphereLight:天空和地面的颜色不同(天空蓝色,地面绿色)

点光源 PointLight:从一个点向四周均匀发射光线。一般用来模拟灯泡。
矩形光源 RectAreaLight:从一个矩形向四周发射光线,用来模拟窗户或者青空灯。
聚光灯 SpotLight:锥形光源,锥形中心向四周减弱,模拟手电筒。
7.2.2 光照相互作用

「环境光(ambient)」
有一些光很难寻找直接光源,比如在无灯的房间,通常也不是一片漆黑的。环境光用来模拟这种非直接光源产生的光照效果。它无方向地均匀照亮所有表面,照亮效果只与光源强度和模型表面本身的特性有关。
「漫反射(diffuse)」
这一交互是决定物体亮度与颜色的主要因素。光照向物体后,被均匀地反射到所有方向,因此,不管观察者的角度如何,物体同一个位置的光照效果都是一样的。照亮效果与光照强度、物体漫反射系数和光照角度与物体表面法线的夹角有关。

「镜面高光(specular)」
但生活中绝大多数物体表面都不是完全粗糙的,因此不会是均匀反光的。光滑的物体在光照对应方向的反射更强一些,产生镜面高光,直至发生镜面反射。

漫反射 光滑 镜面
在 3D 场景渲染中,镜面高光取决于镜面光的光照强度以及物体表面的镜面反射系数。

思考:为什么以前的 3D 游戏,镜子都不能反射出主角?
因为这种光照模型,是基于单个物体表面进行运算的,影响物体表面颜色的,只有物体本身和光源,没有其他物体的反光。对于镜面反射,最后计算的结果只能是表面高光。因此是没有办法做出真正的镜面反射效果的。
怎么解决这个问题呢?两条路径可以走:更好的光照模型 以及 环境贴图。
7.2.3 光照模型
光照模型可以分为 局部光照模型(local illumination models) 和 全局光照模型(global illumination models)。在 局部光照模型 中,物体的反光(即,物体的颜色)仅取决于 「物体表面本身的属性」 和 「直接光源的颜色」,包括 Phong 光照模型和它的改进版,Blinn-Phong 光照模型。而在 全局光照模型 中,会额外考虑光线与整个场景各个物体及物体表面的相互影响,比如多次反射、透射、折射等,需要相当大的计算量,包括光线追踪、辐射着色和光子映射等。
在实时 3D 渲染中,一般只讨论局部光照模型。
冯氏光照模型考虑光照相互作用中的环境光、漫反射和镜面高光,并将它们叠加在一起形成最终颜色。改进版的冯氏光照模型提升了计算镜面高光的精确度和效率。
7.3 多边形着色 - Polygonal Shading
有了光照模型,我们需要确定多边形面的颜色。着色有以下几种方法:
7.3.1 平面着色 - Flat Shading
一个三角形有三个顶点,我们选择一个代表顶点(第一个顶点,或者三角面的法线和颜色均值),在给三角形着色时,针对这个顶点的颜色和法线计算光照效果,并将其结果应用于整个多边形。

这样做的性能很好,因为每个多边形只需要计算 1 次光照。但,它通常会导致模型所有的三角面都清晰可见。一般情况下,这不是我们想要的效果,除非在进行低多边形艺术创作。
7.3.2 高洛德着色 - Gouraud Shading
高洛德着色是一种差值着色方法,首先算出每个顶点的法线,然后对每个顶点计算光照,接着通过 双线性差值(bilinear interpolation) 计算出每个边的光照,再差值出每个像素点的光照。
| 获得顶点的法线 - 邻多边形均值 | 获得边与像素点的光照 - 双线性差值 |
|---|---|
 |
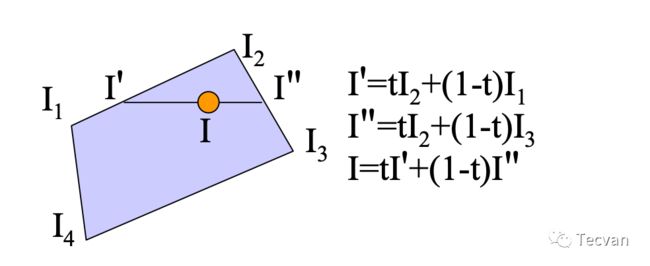 |
这种着色方式可以平滑地渲染出物体表面,但是会丢失一些高光信息。想象一个巨大的三角面,如果这个三角面只有中间的部分产生镜面高光,而顶点没有光照,那么整个平面都将没有光照效果

7.3.3 冯氏着色 - Phong Shading
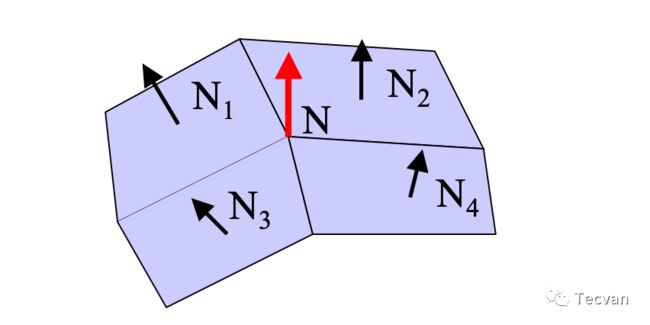
冯氏着色与高洛德着色类似,但是它不是对光照进行差值,而是对法线进行差值,得到每个像素点的法线,并针对每个像素点计算光照。
| 获得顶点的法线 - 邻多边形均值(和上面一样) | 获得边与像素点的法线 - 双线性差值 |
|---|---|
 |
 |

顶点法线,平面着色,高洛德着色,冯氏着色
对比 ThreeJS 示例,了解三种着色方式的区别:
MeshPhongMaterial:https://threejs.org/docs/index.html?q=mesh#api/en/materials/MeshPhongMaterial
打开 flat shading 的 MeshPhongMaterial:https://threejs.org/docs/index.html?q=mesh#api/en/materials/MeshPhongMaterial
MeshLambertMaterial:https://threejs.org/docs/index.html?q=lam#api/en/materials/MeshLambertMaterial
| Flat Shading MeshPhongMaterial* | Gouraud Shading MeshLambertMaterial | Phong Shading MeshPhongMaterial |
|---|---|---|
 |
 |
 |
*区别冯氏光照模型与冯氏着色模型
7.4 纹理贴图 - Texture Mapping
根据之前的理论,顶点颜色的是光照和材质本身的颜色。但是,如果我想实现一面砖墙,添加再多的顶点,再多的光照,再好的着色方法也没办法照出这种效果...

纹理贴图在这个时候就派上用场了。它在不改变几何体本身的情况下,提供了更多的绘制细节。
纹理贴图最初一般指漫反射贴图(diffuse mapping)。它将 2D 纹理上的像素直接映射到 3D 表面上。随着多通道渲染的发展,目前有更多各种各样的贴图。如 凹凸贴图、法线贴图、置换贴图、反射贴图、高光贴图和环境闭塞贴图... 接下来对其中一些进行简单介绍。
7.4.1 漫反射贴图 - diffuse mapping
想象一下,我们给一面白墙贴壁纸,这个应该是比较简单的事情,只要对齐贴好就可以了... 给长方形材质贴到长方形面上,与贴墙纸类似,只需要在 2 维空间,将坐标映射即可。
与贴壁纸一样,这种贴图并不是贴上就没光滑反射、镜面高光等光照效果了,它只影响漫反射的底色。
实践:在 ThreeJS Editor 中,添加一个 PointLight、一个 Plane,并为 Plane 添加 texture map。如果你一切都做对了,应该会看到下面的效果。或者,你可以导入下面的 JSON。
但是有时候,我们需要完成一些 3 维映射,比如,我们在做地球仪,需要将平面的世界地图贴在球面外。或者拿到一张全景照片,在预览时,需要将其贴在球面内。
这时,我们就需要更复杂的映射关系。找到几何体上的坐标 (x, y, z) 与 2D 贴图坐标 (u, v) 的对应关系,一般称为 uv 映射。之前我们在顶点着色阶段提到的 纹理坐标变换 指的就是这个过程。

还有一些复杂几何体,很难找到其上的点与 2D 材质平面的对应关系。对于这种几何体,我们可以用简单几何体(比如球或立方体)将其包裹起来,在简单几何体上应用纹理,当需要绘制复杂几何体上的点的时候,从中心向简单几何体投影,取简单几何体上的纹理信息。
实践:了解 ThreeJS 贴在球面的全景图 和 贴在立方体面的全景图。它们不同角度下四周是否有畸变?是否还有其他的视觉区别?
贴在球面的全景图:https://threejs.org/examples/?q=panorama#webgl_panorama_equirectangular
贴在立方体面的全景图:https://threejs.org/examples/?q=panorama#webgl_panorama_cube
但漫反射贴图只能影响要绘制的像素,不管贴多么 3D 的贴图,一旦放在光照复杂的 3D 场景中,整个物体看起来还是平的。要想让物体有 3D 感且不违和,需要能与光进行互动。
7.4.2 凹凸贴图 - bump mapping
为了解决这一问题,我们可以给在计算光照时提供更多的信息。根据之前的结论,影响光照相互作用以及着色的,除了颜色和材质,还有法线。因此,在实际使用中,为了让物体更有 3D 感,比较常见的方法就是使用 凹凸贴图 中的 法线贴图(normal mapping, 3通道凹凸贴图)。
法线贴图是一张 24 位 RGB 图像,(r, g, b) 分别代表法线 (x, y, z) 从 [-1, 1] 映射到 [0, 255] 后的值。其中特殊的是 z,因为面向相机的物体,法线 z 方向总是负值,我们规定 z 的符号反向后参与映射,这也导致 b 的值总是 >= 128,让法线贴图看起来总是比较蓝。
X: -1 to +1 : Red: 0 to 255
Y: -1 to +1 : Green: 0 to 255
Z: 0 to -1 : Blue: 128 to 255

获得法线贴图,以及将法线贴图贴在平面 Pane 上的效果,可以看到平面变得可以与光互动
诶?这个贴图是怎么来的?好像是左边的场景渲染出来的... 都有对应的 3D 物体渲染出这个贴图了,直接用真实的物体不就好了,为啥还要把它贴在平面上?思考题,后续解答。
7.4.3 移位贴图 - displacement mapping
法线贴上去之后看起来还是很平...因为它只影响法线,并没有影响真正的几何高度,因此在平角(接近 180 度)的角度下就暴露出它本身是平的。
为了修正这个问题,我们可以改为叠加一个移位贴图来影响它的几何高度。移位贴图是黑白的,因为只需要操作高度信息。它在提供更精确的 3D 渲染的同时,添加了大量额外的几何,是同类技术中消耗最高的。过去长期以来一般只用于离线渲染。

实践:在 ThreeJS Editor 中,添加 DirectionalLight、AmbientLight、Plane 和 Box,并为 Box 添加 displacement map。调整 Box Geometry 的曲面数,观察移位贴图的效果。你也可以导入下面的 JSON。
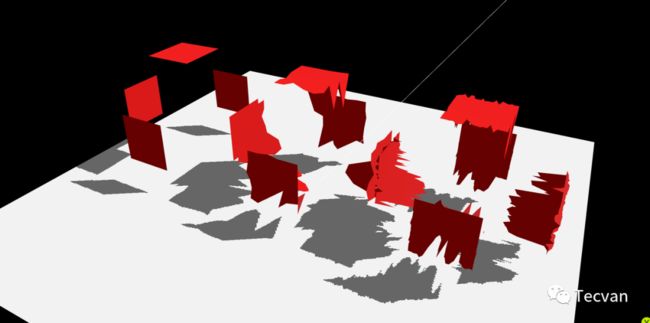
Seg = 1, 5, 20 的效果
7.4.4 环境贴图 - environment mapping
如果这个物体非常光滑,会发生镜面反射,或是非常透明,会发生折射,我们怎么办呢?回顾一下,我们的光是局部光照模型,仅取决于物体表面本身的属性和直接光源的颜色,镜面高光也只是高光... 我真的想做一面镜子,如果上不了光线追踪,应该怎么处理?
这就要请出环境贴图了。
环境贴图与 2D 纹理类似,是在对象外侧围一个 球 或 立方体,并贴入对应纹理。当物体需要绘制反射或折射时,根据反射或折射光路寻找对应在立方体上的材质信息。
实践:了解 ThreeJS 的环境贴图: https://threejs.org/examples/?q=env#webgl_materials_envmaps
| 反射 | 折射 |
|---|---|
 |
 |
「7.4.5 阴影贴图 - shadow mapping / shadowing projection」
阴影贴图就是环境中的阴影信息。
假如用相机替换掉光源,以光源的视角,就能得到场景的深度图像。在绘制场景时,如果对应位置的深度更深,则说明这个位置一定没有被对应光源照射到,可以忽略光的渲染...
对每一个光源都这样做,就可以绘制出阴影的效果。

7.4.6 贴图的意义
有时候我们在玩 3D 游戏的时候,有些物体明明存在,但在水面或者镜子中却看不到它,或者在阳光下其他的物体都有阴影,它却没有影子,为什么?
因为在局部渲染模型中,实时渲染它们的代价很高,因此,它们通常都是贴图!如果预先渲染的环境贴图或者阴影贴图上没有对应的元素,那自然就不能在反射效果或阴影中看到他们。为了提高性能,需要将场景中的一些内容预先、离线地渲染为贴图,这一部分也叫贴图的烘焙。
7.5 多通道渲染 - Multiple-pass Rendering
有这么多事情要做,一次性做完很难,因此我们可以通过多通道渲染,每次完成不同的工作后,通过某种算法合并起来。这样,每一步都可以分别缓存。当场景发生变化时,一些已经完成的通道渲染可以保持不变。

*beauty pass 具体指代什么似乎没有定论,这里指默认的不考虑场景作用关系的渲染。
实践:了解 ThreeJS 的多通道渲染: https://threejs.org/examples/?q=ao#webgl_postprocessing_sao
通过右上角的控制组件调整输出,观察 默认(Beauty)、环境闭塞(AO)、阴影(Depth) 和法线(Normal) 的输出,以及合并后的输出。
| Beauty | AO | Depth | Normal |
|---|---|---|---|
 |
 |
 |
 |
7.6 后处理 - Post Processing
整个渲染流程结束后,我们有各个阶段的所有输出,以及最终所有像素点的信息。此时,我们还有机会对整个场景进行变换,应用一些效果。这一阶段就是后处理。
一些常见的后处理阶段做的事情:边缘检测、物体发光、体积光(上帝光束)、信号故障效果。
实践:了解一些常见的 Post Processing:https://vanruesc.github.io/postprocessing/public/demo/#antialiasing
| 边缘检测 | 发光 | 体积光 |
|---|---|---|
 |
 |
附录
参考资料:
文章组织方式的参考:https://www.uni-weimar.de/fileadmin/user/fak/medien/professuren/Computer_Graphics/course_material/Graphics___Animation/5-GFX-pipeline.pdf
细节内容参考:https://www.logiconsole.com/real-time-rendering-1/
渲染管线中文 PDF:https://positiveczp.github.io/%E7%BB%86%E8%AF%B4%E5%9B%BE%E5%BD%A2%E5%AD%A6%E6%B8%B2%E6%9F%93%E7%AE%A1%E7%BA%BF.pdf
流程参考:https://zhuanlan.zhihu.com/p/61949898
资源:
Shaders:https://thebookofshaders.com/
ShaderToy:https://www.shadertoy.com/view/llj3zV
免费或者付费的 3D 模型:https://sketchfab.com/3d-models?features=downloadable&sort_by=-likeCount
